|
SCAO NANOSATELLITE REPERTOIRE DES REGULATIONS AVEC MAGNETOCOUPLEURS & UNE ROUE |
![]()
![]()
Cadre de la synthèse : cette page propose une synthèse des techniques de SCA essayées, notamment dans ce site, pour le pilotage en attitude d'un nanosatellite. Bien évidemment, toutes celles existantes n'y sont pas répertoriées et l'auteur ne fait que rassembler celles qui ont été testées en simulation, pour permettre à des étudiants associés à un projet de nanosatellite, de faire les choix adaptés à leur mission. Les références aux articles spécialisés seront fournies.
Les seuls actionneurs utilisés seront des magnétocoupleurs ( 2 ou 3 ) et une seule roue, sur le tangage. Pas question de 3 roues ou de tuyères supplémentaires.
On y trouvera en particulier :
- La réduction des vitesses en "détumbling"
- La mise en spin du satellite à vitesse fixée autour d'un axe fixé ( lié au satellite ou pas, soleil, axe inertiel )
- L'annulation ou la réduction éventuelle d'un spin par une roue, pour part exemple lancer la roue en rotation
- La régulation fine autour d'une attitude de travail ( petits angles ou pas )
- Des manœuvres de retournement ou de pointage particulier ( soleil, direction inertielle...)
- La suivi du soleil pour améliorer l'énergie produite par les panneaux ( précession vers le soleil ou pointage )
- Le pointage soleil en mode survie
Or on ne connaît dans l'espace que 2 champs créant des forces ou des couples externes: la gravitation et le champ magnétique local.
Pour la création de couples internes, on fait appel à des roues de réaction. Une roue interagit sur l'attitude du satellite de 2 façons bien distinctes :
- Par le couplage gyroscopique avec la rotation absolue satellite, c'est le niveau de la vitesse roue qui détermine l'intensité du couplage
- Par un effet réactif, lors des changements de vitesse de rotation de la roue, par échange de moment cinétique entre la roue et le satellite
Le champ de gravitation étant conservatif, n'a aucune chance de pouvoir être utilisé pour réduire des vitesses angulaires ou contrôler une attitude, tout au plus pourra-t-il participer à une stabilisation finale, grâce au couple du gradient de gravité présent pour les satellites à matrice d'inertie non sphérique.
1°) UTILISATION DU CHAMP MAGNETIQUE :
Il ne reste que le champ magnétique, utilisable via des bobines d'induction ( magnétocoupleurs ou magnéto torquers ), parcourues par des courants adéquats, créant un moment magnétique interne M qui interagit avec le champ magnétique externe pour créer un couple C, participant à la commande sur le satellite.
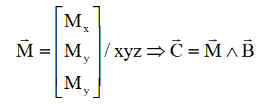
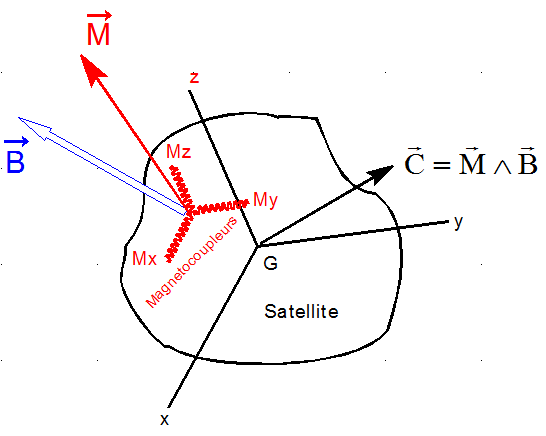
Limitation évidente : L'expression du couple magnétique montre qu'il est impossible de générer un couple dans la direction de B. Fort heureusement le champ est variable et ce qui ne peut être réalisé à un endroit peut l'être ailleurs.
2°) CONTRAINTES FONCTIONNELLES :
Les bobines sont limitées en moment magnétique. Le moment magnétique maximum est noté Mmax.
Une roue est limitée soit en vitesse de rotation maximale Wmax , soit en couple maximum Cmax.
Ces valeurs s'obtiennent sur les descriptifs techniques des matériels. Nous allons voir que ceci entraîne un mode de calcul optimisé et compatible avec les contraintes.
a) Optimisation du moment magnétique :
Lorsqu'un moment magnétique est calculé, seule la composante perpendiculaire à B est utile. Il n'est donc pas nécessaire de garder celle qui est portée par B. Nous prendrons donc toujours :
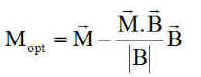
b) Respect des contraintes fonctionnelles :
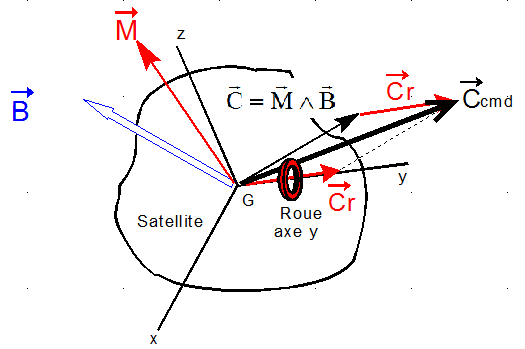
Le vecteur couple de commande de SCA, Ccmd a été élaboré avec les techniques mathématiques adaptées. Il est supposé connu. Il va donc falloir déterminer à la fois le moment magnétique à construire M ( avec les courants bien choisis ) et le couple roue Cr. La commande n'est acceptable que si
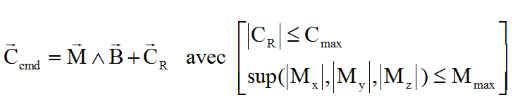
Lorsque les conditions ne sont pas remplies, il est impératif de garder la direction de la commande, on opère alors une réduction proportionnelle, comme ci-dessous:
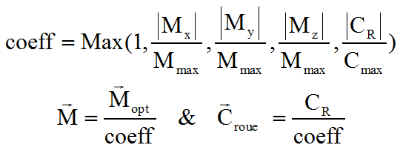
3°) COMMENT CONSTRUIRE UN COUPLE DONNE A L'AIDE DE MAGNETOCOULEURS AVEC OU SANS ROUE :
C'est tout l'enjeu d'une régulation de ce type, avec une technologie minimale.
a) Rappels : disons rapidement qu'en injectant des courants d'intensité Ix Iy Iz dans des magnétocoupleurs d'axe x y ou z liés au satellite, on peut créer tout moment magnétique M. Voir explications.
b) Limitation : Comme indiqué ci-dessus, on peut créer tout couple normal au champ magnétique, mais pas de couple sur l'axe du champ magnétique. C'est une contrainte sévère, fort heureusement adoucie par la variabilité du champ, le long de l'orbite.
c) Commande à 3 magnétocoupleurs: uniquement exploitable pour des couples de commande orthogonaux au champ B. Dans ces conditions
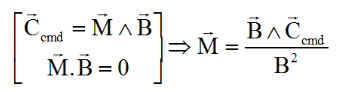
d) Commande à 2 magnétocoupleurs et une roue: Retrouver la théorie
RÈGLE IMPORTANTE
" En orbite non polaire, quel que soit le champ magnétique B, non perpendiculaire à l'axe tangage, et le couple C à réaliser
- 2 magnétocoupleurs de moments mx et mz d'axes x et z et une roue de réaction d'axe y
permettent toujours de générer ce couple C de telle manière que
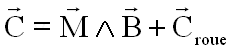
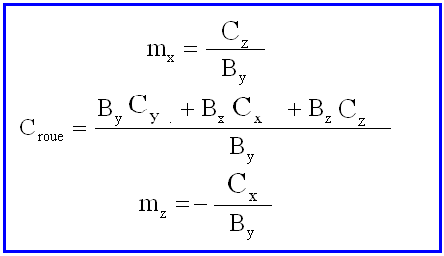
e) Désaturation ou inversion de vitesse d'une roue avec 2 magnétocoupleurs:
Une roue peut fonctionner suivant 2 modes :
- Cas 1 : A vitesse constante, seul son moment cinétique est utile pour stabiliser une direction ou donner le bon choix de l'équilibre, lors d'un pointage
- Cas 2 : Pour son couple réactif, comme actuateur, pour "contrer" des couples parasites.
Le cas 2 révèle alors que la vitesse de la roue ne peut qu'augmenter en moyenne sous l'effet moyen non nul des perturbations. Il s'ensuit que la roue pourrait sortir de la plage des vitesses limites imposées par la technologie. On parle de saturation de la roue.
Le cas 1 peut, par exemple pour un retournement nécessiter un changement de signe du moment cinétique, ce qui revient à inverser la rotation de la roue.
Dans les 2 cas l'opération ne doit pas déstabiliser le satellite et donc l'action nécessaire sur la roue, qui se répercute sur le satellite, doit s'accompagner de l'effet opposé sur le satellite généré par les magnétocoupleurs.
Dans tous les cas on passe d'une vitesse w0 à une vitesse -w0, w0 vitesse de croisière du cas 1, w0 vitesse maximum wmax ( > 0 ou < 0 ) du cas 2. Si la loi de couple ( - CR couple satellite sur roue ) est linéaire sur une durée Dt, le lecteur vérifiera, J désignant le moment d'inertie de la roue:
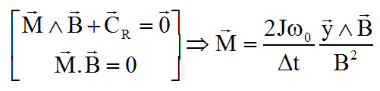
Moment magnétique toujours réalisable avec 2 magnétocoupleurs sur les axes x et z.
II TECHNIQUES DE RÉDUCTION DES VITESSES ANGULAIRES :
Lorsqu'un satellite est mis en orbite, la libération s'accompagne de vitesses angulaires importantes, pouvant atteindre quelques dizaines de degrés par seconde, dans le pire cas. Dans ce cas là, abandonné comme un caillou dans l'espace, incapable de communiquer à coup sûr avec le sol, la réduction des vitesses ne peut se faire que de manière autonome, en n'utilisant que les ressources interne en calcul et l'environnement spatial.
1°) Technique la plus simple dite en B-dot ou Bpoint à 3 magnétocoupleurs: Objet d'un brevet en 1994 déposé par M Damilano
But à atteindre : réduire les vitesses angulaires après la mise en orbite
Elle utilise la dérivée du champ magnétique B vu du satellite. Effectivement, la partie principale de cette dérivée est représentative des mouvements angulaires du satellite, car la dérivée due au mouvement orbital est faible.
|
. |
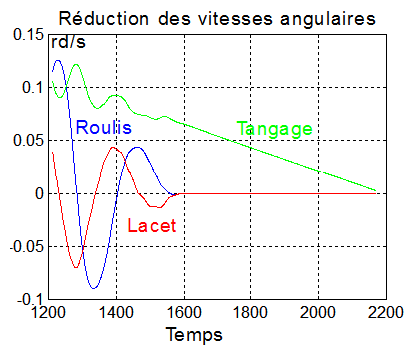
regderb1/regderb1.m
Commentaires :
Cette régulation est excellente pour dissiper l'énergie de rotation des vitesses initiales en "tumbling". Elle ne conduit bien sur pas à la stabilisation. Le lecteur intéressé pourra consulter l'optimisation de la méthode sur l'étude complète qui lui est consacrée sur ce site
Récupérer les fichiers de simulation
2°) Technique de STEYN à un seul magnétocoupleur sur le tangage y:
But à atteindre : réduire la rotation transverse à l'axe de tangage
La figure suivante montre qu'un excellent moyen de détecter la rotation transverse wT à l'axe y, est de suivre l'angle b.
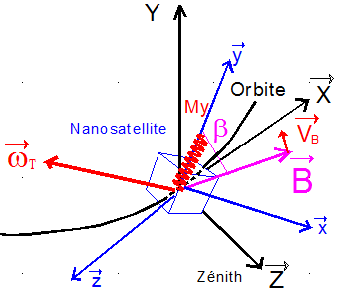
Steyn propose donc, une loi de commande avec un seul magnétocoupleur d'axe y : en effet
|
|
Liens utiles : Adresse 2 Adresse 3 Adresse 4. Récupérer les fichiers
Commentaires : Voir explications
- Régulation utilisable lorsqu'on souhaite conserver un spin autour de l'axe y, spin qui peut aider à une stabilisation avec y normal au plan orbital (Y-Thomson attitude )
- On peut montrer qu'elle dissipe l'énergie cinétique due à la rotation transverse. Elle est particulièrement utile en "détumbling" après l'injection donnant lieu à des vitesses angulaires importantes.
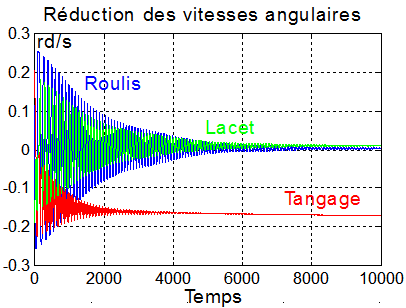
steyn_1/tumble_1.m
3°) Technique de base de LAURENS ( proportionnelle ) à 3 magnétocoupleurs:
But à atteindre : réduire les vitesses angulaires après la mise en orbite
Elle consiste à définir un repère de consigne Rc = ( Xc Yc Zc ) qui est la configuration finale à atteindre par le repère satellite xyz. Par exemple Rc est le repère orbital classique XYZ d'une orbite circulaire, avec X unitaire de la vitesse, Y unitaire du moment cinétique orbital et Z l'unitaire du rayon vecteur, donc vers le zénith.
Dans ce repère de consigne, le vecteur champ magnétique B a pour composantes ( Bc1 Bc2 Bc3 ).
L'idée de M LAURENS est de transposer ces composantes dans le repère satellite xyz, pour en faire un vecteur de consigne Bc ( champ magnétique de consigne )
Bc = ( Bcx Bcy Bcz ) = ( Bc1 Bc2 Bc3 )
qui sert de "boussole" pour la régulation, en ce sens que l'on doit aligner B vu du satellite sur Bc.
Le moment magnétique le plus simple, adopté est:
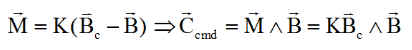
De toute évidence, la présence de B dans la première formulation est inutile avec le produit vectoriel qui l'élimine, ce qui conduit M Laurens à choisir, le plus simple soit :
|
3°) Technique de LAURENS améliorée ( Proportionnelle-dérivée ) à 3 magnétocoupleurs:
Elle reprend la régulation précédente et lui ajoute un terme proportionnel à la dérivée de l'écart de consigne. Monsieur Laurens normalise l'expression en divisant par la norme de B.
|
Commentaires : Si on imagine au mieux que la régulation conduit à un couple de commande quasi nul, alors on a, en appelant P la matrice de passage de Rc (consigne ) à R ( satellite ), et considérant que ni Bc ni B ne peuvent être nuls:
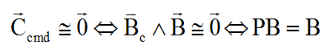
Le vecteur B est donc un invariant du changement d'axes qui ne peut donc être qu'une rotation autour de la direction de B, qui nous le savons est incontrôlable par magnétocoupleurs.
Il ne faut attendre de la régulation de Laurens que la réduction des vitesses mais absolument pas un pointage quelconque, que rien d'ailleurs ne définit dans la régulation. Le tangage est maîtrisé, seule peut subsister une rotation transverse de l'ordre maximum de 0.03 rd/s. La qualité du résultat dépend des conditions initiales, mais dans tous les cas la stabilisation n'est pas obtenue. Retrouver les fichiers
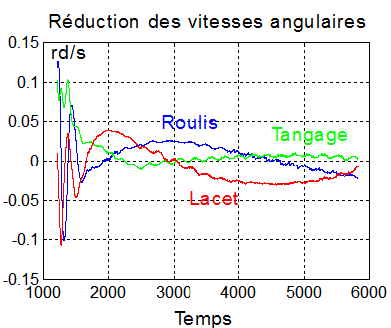
regbous0.m dans regbous0.zip |
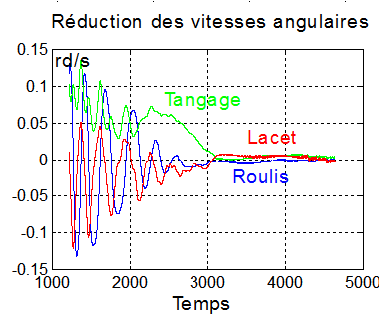
regbous1.m dans regbous0.zip |
Renseignements complémentaires sur la régulation "boussole" : Voir sur ce site Brevet de M Laurens Brevet équivalent
NB : La technique ci-dessus sera prolongée par le mode acquisition et régulation fine ( à voir plus loin )
III TECHNIQUES DE MISES EN SPIN :
La mise en spin choisie d'un satellite peut être nécessaire dans diverses configurations :
- Une phase intermédiaire de la stabilisation complète, le spin peut servir à garder momentanément une attitude stable, avant d'être réduit ou supprimé par une roue qui utilise ce spin pour atteindre sa vitesse de croisière, surtout quand elle doit travailler à vitesse constante.
- Un passage en mode survie, pour préserver la mission dans l'attente d'une réparation. L'axe de spin peut alors pointer le soleil, pour la réception maximale d'énergie. Le spin peut aussi servir à stabiliser le satellite, dans une configuration proche de celle de travail.
Nous retrouvons donc nos deux savants techniciens, STEYN et LAURENS
1°) Technique de M DAMILANO et DEFENDINI à 3 magnétocoupleurs: Voir le brevet voir Explications sur ce site
Elle conserve la régulation de réduction des vitesses utilisant la dérivée du champ magnétique en axes satellite et la complète par un terme de mise en spin.
w désigne la vitesse finale du spin et u sa direction unitaire
|
Exemple de mise en spin à 0.0088 rd/s, autour de y. regspin0.m à extraire de regspin0.zip
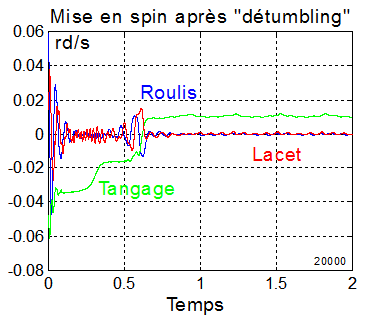
NB : Cette régulation annule les vitesses autres que le spin, mais ne stabilise pas les angles. Elle ne peut faire partie que d'une régulation initiale avant acquisition des angles et contrôle fin.
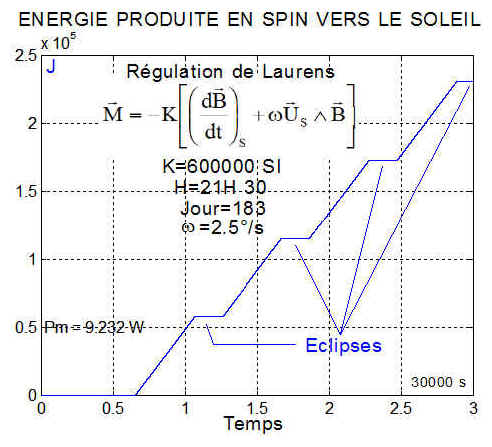
Autre exemple en survie, avec mise en spin vers le soleil de vecteur unitaire Us en axes satellite, simulation laurspin/SurvSpin.m initialisée par surv2dat.m: Explications détaillées Retrouver les fichiers
2°) Technique de M STEYN à 3 magnétocoupleurs: Brevet voir Explications détaillées sur ce site
La commande la plus générale donnée par WH Steyn, Y Hashida et V Lappas ( voir Adresse 4 ) utilise en parallèle 2 régulations :
- Les magnétocoupleurs sur les axes xe z pour la mise en spin à la vitesse angulaire de référence qref
- Le magnétocoupleur d'axe y en réduction de vitesses angulaires de type Bpoint, exposée plus haut
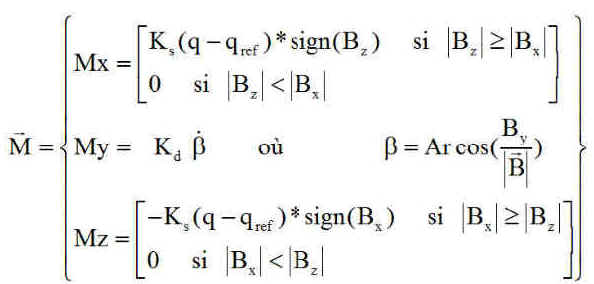
Cette action précède l'acquisition et la régulation fine en mode travail. Ci-dessous une mise en spin autour de y à -3.2°/s après "détumbling"
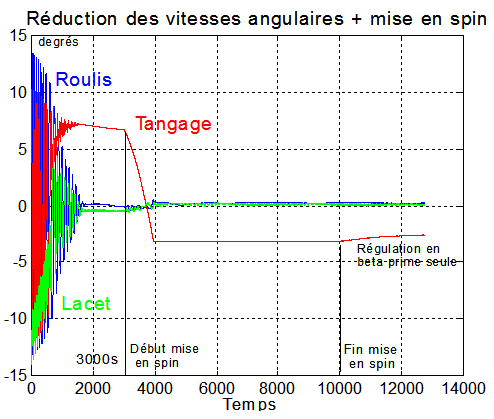
IV TECHNIQUES DE RETOURNEMENT :
La technique utilisée est celle de Philippe Laurens utilisant un repère Rc et un champ Bc de consigne. Les exemples concernent la situation de base avec le satellite stabilisé 3 axes xyz coïncident avec XYZ.
|
Retournement autour de X
Xc=X Yc=-Y Zc = -Z Bc/xyz = [BX - BY - BZ ] & wroue < 0 |
Retournement autour de Y
Xc=-X Yc=Y Zc = -Z Bc/xyz = [- BX BY - BZ ] & wroue > 0 |
Retournement autour de Z
Xc=-X Yc=-Y Zc = Z Bc/xyz = [-BX - BY BZ ]& wroue < 0 |
Les simulations sont nanolaur/Ret180_X.m, Ret180_Y.m, Ret180_Z.m initialisées par nanodat0, dans lesquelles il suffit de changer le vecteur de consigne Bc et de prendre une vitesse roue qui s'accorde avec le mouvement orbital.
Ci-dessous un retournement autour de l'axe Y, le quaternion Q=[1 0 0 0] devient Q=[0 0 1 0], montrant que l'axe de la rotation est Y et que l'angle est tel que sin(a/2)=1 donc de a = 180°. C'est bien un retournement complet. La précaution avait été prise de choisir une vitesse de roue < 0.
|
Quternion(2:4=) passe de [0 0 0] à [0 1 0] |
Quaternion(1) passe de 1 à 0 |
Retrouver les simulations Ret180_X.m, Ret180_Y.m, Ret180_Z.m dans nanoalaur.zip
Commentaires :Le résultat est remarquable et doit pouvoir être généralisé à tout retournement d'une situation stable dans un repère R1 à une autre dans R2 par rotation de 180° autour de l'un des axes de R1.
1°) Techniques de STEYN : Voir explications détaillées Voir le brevet
a) Réduction des vitesses et mise en spin: La commande totale commence par la régulation vue plus haut, avec "détumbling", spuis mise en spin ( choisi en fonction de la manœuvre de la roue ), suivie de la mise en route de la roue jusqu'à sa vitesse de croisière:
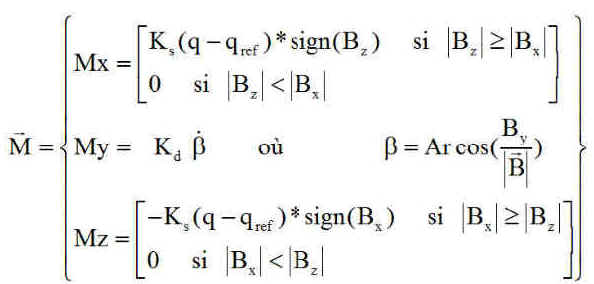
b) Annulation du spin par mise en route de la roue :
Les données de la roue permettent de calculer la vitesse angulaire de référence et donc le couple qui permet d'annuler cette vitesse, une fois le temps d'action DT fixé.
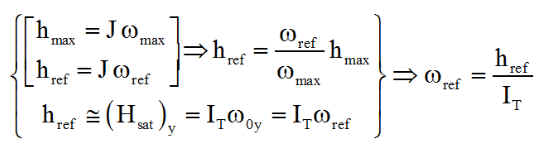
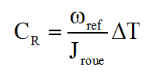
C'est l'objet de la première simulation TUMBLE00.M initialisée par STN5DAT.M qui stocke le vecteur d'état final dans InitFin.mat ( variable init_sca_fin ) qui initialisera la simulation fine de c). Voici une idée des séquences.
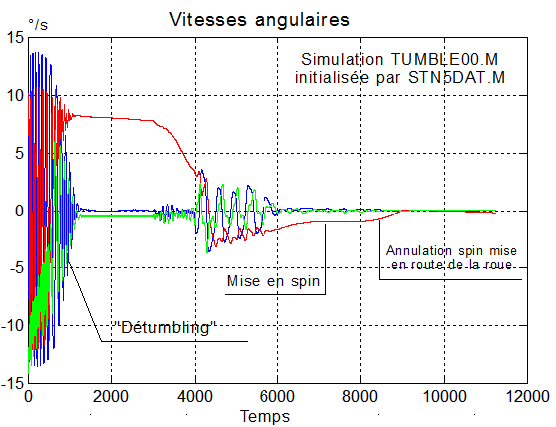
c) Une régulation fine : comme ci-dessous est mise en oeuvre, avec 2 buts:
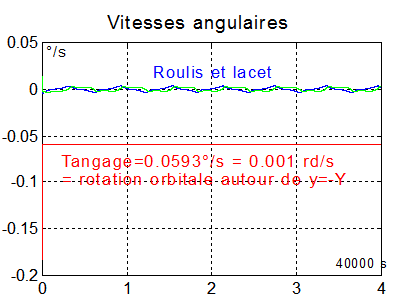
- Contrôler les rotations transverses ( wX et wZ )en axes orbitaux et simultanément maintenir le moment cinétique de la roue à son niveau de croisière initial
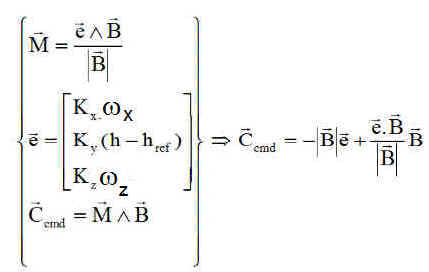
w0 est la mesure arithmétique de la vitesse de rotation orbitale ( 0.001 rd/s en valeur absolue )
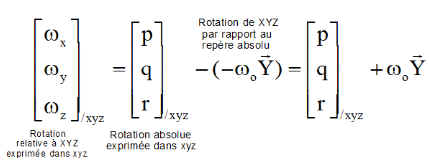
L'ensemble fait l'objet de la simulation SCA00FIN.M initialisée par STN00DAT.M ( Retrouver les fichiers sca_complet_steyn.zip)
 |
|
2°) Régulation complète mode Bpoint + commandes PID sur les 3 axes :
En 2 temps : simulation totale2.m retrouver les fichiers nanosat0.zip
1 - "Détumbling" en mode Bpoint sur 6000 s, jusqu'à un seuil de vitesse angulaire de 0.003 rd/s = 0.18°/s
2 - Acquisition puis mode fin, sur régulation PID des 3 angles par 2 magnétocoupleurs et une roue de réaction, durant 3000 s. Arrêt sur seuil angulaire de 1°. Les couples PID sont élaborés autour des axes de mesure des angles de Cardan, puis convertis en couples sur les axes satellite.
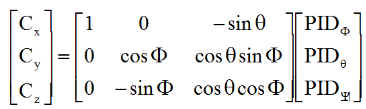 |
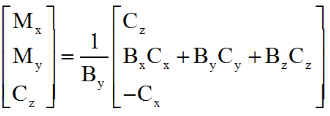 |
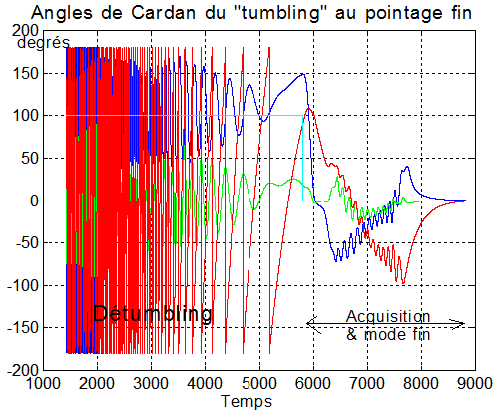
3°) Régulation complète mode Bpoint + commande PD sur l'axe du quaternion : strictement personnelle, jusqu'à nouvel ordre.
En deux temps successifs
1 - "Détumbling" en mode Bpoint sur 5000 s, jusqu'à un seuil de vitesse angulaire de 0.002 °/s, pour basculer en mode fin.
2 - Acquisition et mode fin, sur régulation PD de l'angle de rotation du quaternion ( 2 magnétocoupleurs et une roue de réaction ). Arrêt sur seuil angulaire de 5°
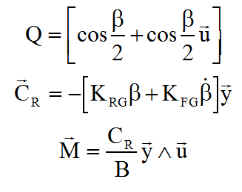
Régulations : regboux2.m suivie de regboux6.m, avec vue sur l'ensemble des résultats. Retrouver les fichiers avec nanosat8.zip
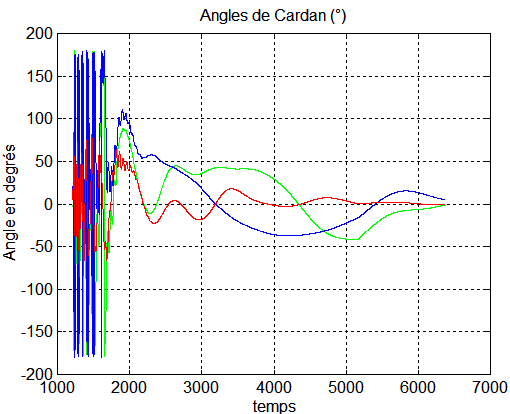
4°) Régulation complète mode Bpoint de Laurens + une roue à vitesse constante :
Théorie sur ce site Brevet de M Laurens Retrouver les fichiers dans nanolaur.zip ou laursurv.zip
But: aligner les axes satellites sur les axes du repère orbital avec y sur Y en pointage zénith ou -y sur Y en pointage nadir Choix du type de pointage par la constante zenith ( 1 pour le zenith et -1 pour le nadir ), dans nanodat0 |
nanolaur/nanosim0 ou laursurv/nanosim0
Voir la page spéciale et complète des résultats
La régulation utilise la technique de base de M Laurens avec un champ magnétique de consigne, correspondant au repère de consigne R00 = XYZ = repère orbital. En parallèle, une fois le tumbling bien réduit, l'acquisition des angles et le mode fin sont atteints.
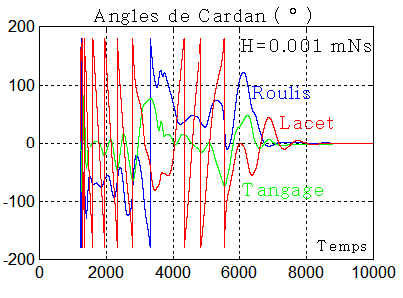
Cas d'un pointage ZENITH
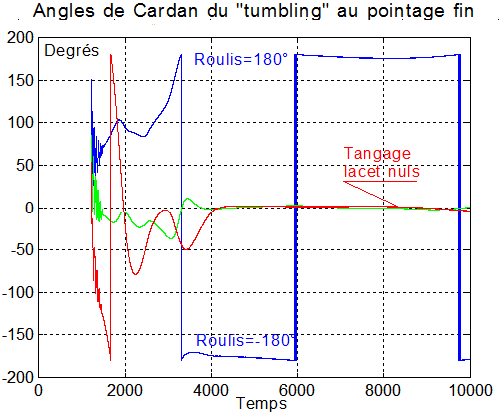
Cas d'un pointage NADIR
NB : Cette régulation est certainement la plus simple et pour moi la meilleure. La production énergétique correspond à une puissance moyenne/orbite de 8.3 W
Remarque : Le pointage zénith donne lieu à une meilleure précision angulaire que le pointage nadir. Vérification faite ce sont les produits d'inertie qui font la différence.
L'ensemble complet : "Détumbling" +Acquisition et pointage fin+satellite libre+Régulation fine+satellite libre +Régulation fine+..... +régulation fine et désaturation+satellite libre+....est en démonstration, dans le cas où au final, on travaille sur de petits angles.
Exécuter totale2.m puis reg_pert.m puis regdesat.m puis reg_pert.m ..etc..
NB : reg_pert est le comportement libre sous l'effet des perturbations seules
VII MODE SURVIE AVEC POURSUITE DU SOLEIL ( Technique STEYN ) :
Dans un mode survie, l'énergie reçue par période ou encore la puissance moyenne est le paramètre à privilégier, accompagné d'une consommation minimale d'énergie.
Deux modes ont été étudiés en relation avec les techniques de Steyn ou de Laurens.
1°) Mode de poursuite en précession vers le soleil ( type Steyn ):
C:/casasurv/surv_sim.m initialisée par surv_dat.m
Durant les périodes d'éclairement la face qui porte les panneaux doit être éclairée au maximum, choisissons la face +y. Steyn imagine de faire précessionner l'axe y vers le solail par la loi de moment magnétique M:
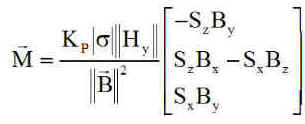
Cas des panneaux côté y+, sinon changer S en -S |
M :moment
magnétique à générer
Hy moment cinétique de la roue à vitesse constante s angle entre la direction y et la direction S du soleil Sx Sy Sz composantes de l'unitaire soleil dans les axes satellite Kp gain de la régulation |
Références : Théorie sur ce site Brevet de M Steyn PDF sur ce site Retrouver les fichiers
2°) Mode de mise en spin autour de la direction soleil ( type Laurens ): Rappelons ce qui a été vu plus haut:
C:/casasurv/laurspin/SurvSpin.m initialisée par surv2dat.m
Elle conserve la régulation de réduction des vitesses utilisant la dérivée du champ magnétique en axes satellite en parallèle avec un terme de mise en spin.
w désigne la vitesse finale du spin et S sa direction unitaire, celle du soleil,
si les panneaux sont côté y+, sinon S est changé en -S
|
Références : Voir la théorie sur ce site Retrouver les fichiers
VIII MODE SURVIE AVEC ATTITUDE INERTIELLE OPTIMALE POUR L'ENERGIE :
L'idée est de mettre le satellite dans une attitude simple, avec l'axe y+ de sens contraire à Y, la roue en spin négatif constant autour du tangage. Le satellite est inertiellement quasi fixe ( au détail près de la précession de la ligne des nœuds ) dans le plan orbital, de manière à verrouiller l'éclairement solaire tout au long de l'orbite et de l'année.
Le plan ( x,z ) du satellite doit rester confondu avec le plan orbital (X,Z), avec décalage angulaire fixe autour de Y bien étudié pour fournir une énergie optimale .
Le champ de consigne est :
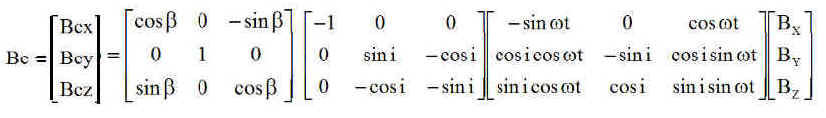
Avec i pour l'inclinaison, t le temps orbital mesuré depuis le survol de l'équateur, au nœud ascendant, w la vitesse angulaire orbitale, b l'angle d'orientation de l'axe z du satellite mesuré autour de y, à partir de Zn*
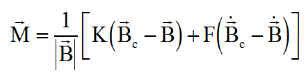
Simulation survfix1.m initialisée par beta_dat.m. L'angle b s'appelle beta_fix dans l'initialisation beta_dat.m où un programme intégré calcule directement b.
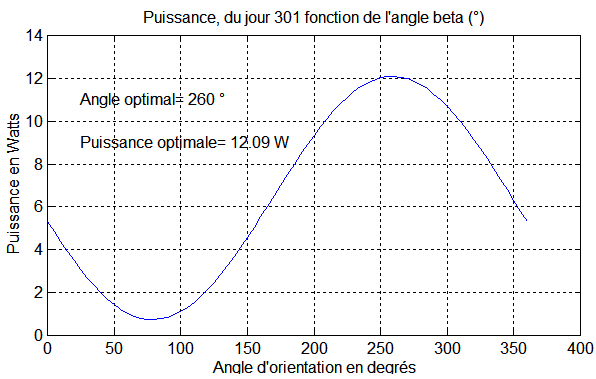
L'angle b peut se calculer séparément, par le programme balayage.m ( le retrouver ) qui fournit, pour un jour J donné, l'angle b optimal et la puissance optimale attendue.
La régulation est la plus simple qui soit, celle de Laurens, de type proportionnel dérivée sur la différence entre le champ de consigne Bc et le champ réel B.
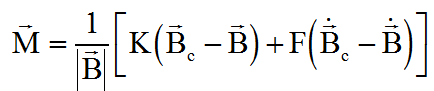
K = 1.6 e-5 SI F = 8.4 e-3 SI
Le lecteur pourra se convaincre du concept en lisant la théorie ( Voir la théorie ) puis en consultant la page détaillée et vérifiée des résultats de la simulation indiquée plus haut ( retrouver les fichiers )
********************* Fin **********************