|
PROPOSITIONS DE MODES DE SURVIE |
![]()
![]()
I PRÉLIMINAIRES
Normalement, dans toute mission spatiale, un mode de fonctionnement dit " MODE SURVIE " est prévu pour permettre la gestion d'un incident important demandant du temps de réflexion et des reconfigurations éventuelles des systèmes de commande ou de la mission elle-même.
Ce mode est activé en présence d'un problème grave. Le but est de mettre assez rapidement le satellite dans un configuration stable et prévue, dite de sécurité, permettant un contact radio avec le sol et une alimentation suffisante en énergie pour gérer les ressources vitales.
NOTES EXPLICATIVES FOURNIES POUR IMAGINER UN MODE SURVIE
On bascule toujours d'un mode à l'autre par un ordre du sol. Le détumbling n'est pas considéré comme un mode car transitoire. Le mode mission doit permettre de mener à bien la mission suivant une certaine stratégie, les mesures, les photos, le SCAO, les télécom ne doivent pas mettre à mal les batteries.
On ne programme les stratégies du mode mission en fonction du niveau des batteries. Le mode survie est un mode où le SCAO doit moins consommer (on arrête la roue, le satellite va se remettre à spiner autour de Ysat), pas de photo, télécom réduites à minima, mesures uniquement pour le SCAO et recharge des batteries.
Si dans ce mode on contrôle les vitesses angulaires (0 autour de Xsat et Zsat et OmegSpin=1°/s autour de Ysat) tout en maintenant Ysat perpendiculaire au plan orbital (-Y) on est dans le cas du contrôle détumbling, mais à la fin avec une puissance dépensée par les magnétocoupleurs faible et un calculateur qui fonctionne , la normale au panneaux va effectivement décrire un cône de demi angle au sommet de 35° à la vitesse angulaire proche de OmegaSpin car >>fréquence orbitale.
L'énergie récupérée doit être proche de celle récupérée en mode mission. En ce qui concerne les antennes il semble que celles que nous utiliserons ont équipé un satellite sans SCAO (mode caillou) et ont pu assurer la communication. On devrait avoir plus d'information, pour l'instant on nous a dit que les vitesses angulaires ne devaient être pas trop grandes pour assurer la communication...
En ce qui concerne l'héliosynchronisme, les paramètres orbitaux sont déterminés par un propagateur d'orbite embarqué et mis à jour régulièrement par une remontée des TLE. Nous devons étudier cette année la fréquence des remontées. L'intérêt d'avoir l'axe de spin qui angulairement parlant est plus proche du soleil est de charger plus rapidement les batteries, à condition que le contrôle ne soit pas trop coûteux en énergie.
Sur le choix des axes, en mode nominal le repère satellite xyz coïncide avec le repère orbital XYZ.
Si
le mode survie a une stratégie détumbling uniquement Y coïncide avec y, et on
devrait récupérer autour de 8,9W orbital dans le meilleur cas mais 7,4 W
orbital en pire cas (le cas dimensionnant) suivant la saison.
Si on adopte le suivi du soleil hors éclipse (et spin autour de y en éclipse) effectivement XYZ ne coïncide plus avec xyz les rotations autour de x et z semblent d'après tes calculs augmenter. Il faudrait toutefois pouvoir récupérer plus de 8W orbital! Si on reste dans ce mode au bout de combien d'orbites -y s'aligne sur le soleil ? car on devrait alors récupérer en puissance orbitale une valeur supérieure à 12*cos(35°)=9,8W quelle que soit la saison. A la limite l'idéal serait d'aligner la normale aux panneaux sur le soleil (donc -y au bon endroit ce qui est plus difficile à réaliser) pour récupérer dans l'absolu 12W orbital.
Après il faut en déterminer le coût car c'est le bilan énergétique qui sera
dimensionnant (mais d'après nos dernières informations sur les modèles de vol
comme la carte processeur les consommations sont supérieures à ce que l'on
avait prévu...). Sachant de plus qu'un suivi du soleil demande la mise en place
de senseurs solaires que l'on avait pas envisagé jusqu'à présent.
Limitons nous aux orbites héliosynchrones, donc quasiment polaires. La position du soleil ( importante sur le plan énergétique ) vue de l'orbite dépend de l'heure au nœud ascendant: Voici 2 cas plutôt simples:
H = 12 h ou 24 h : alors la direction du soleil, en période d'éclairement est proche du plan orbital. Dans ce cas là, si les panneaux sont dans un plan P, et si A ou B sont 2 axes orthogonaux dans P, la mise en "spin" autour de A ou B assurera un éclairement partiel des panneaux solaires. Ce mode est dit "MODE BARBECUE" car le système ressemble à une rôtissoire ( satellite ) avec le soleil la source de chaleur ( mieux lumière ).
H = 6 h ou 18 h : alors la direction du soleil, en période d'éclairement est proche de l'axe tangage du plan orbital. Dans ce cas là, si les panneaux sont dans un plan P, et si A est un axe orthogonal à P, la mise en "spin" autour de A assurera un éclairement satisfaisant des panneaux solaires, hors éclipse. Ce mode est dit "MODE MOULIN A VENT" car le système ressemble à une moulin ( le satellite ) avec le soleil ( la source de vent , mieux la lumière ).
Pour le satellite ( ci-dessous ) que nous étudions, l'heure au nœud ascendant est 21 h 30, exactement à mi-chemin des 2 cas précédents. Elle n'est pas optimale pour ces 2 modes!!! Mais elle est imposée par le lanceur sur lequel le satellite n'est qu'un passager secondaire.
DONNEES ORBITALES :
Orbite héliosynchrone, quasi polaire, circulaire Altitude : 817 km Inclinaison : 98,7
° Excentricité : 0,001165 Période orbitale ~ 104 minutes Heure locale au nœud ascendant : 21h30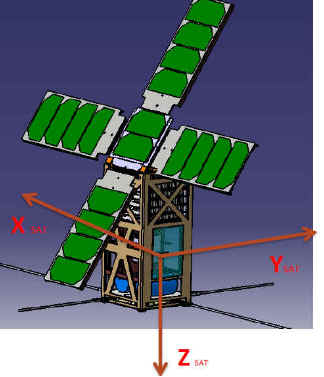
Arrivé à 55° d’inclinaison, le panneau solaire
est bloqué par les butées d’un côté et les ressorts de l’autre.
Nous savons, pour économiser la consommation du SCAO, que nous devrons éventuellement mettre le satellite en spin, pour assurer une stabilisation gyroscopique. Les antennes sont prévues, en fonctionnement nominal, avec leur plan constamment horizontal, lorsque le pointage est nadir ou zénith. Elles pourraient donc maintenant tourner !!! Ce qui pourrait poser problème.
Trois spins sont envisageables :
- Autour de X, qui ressemblerait à un mode ' barbecue ', avec le plan des antennes pratiquement jamais horizontal. Cependant l'antenne parallèle à X reste toujours horizontale, mais risque d'être momentanément masquée par le plan des panneaux , à chaque tour lorsque l'axe Z est orienté zénith. Reste à voir si la deuxième antenne qui est alors proche de l'horizontale est ou non dans l'ombre radio des panneaux? L'axe X présente l'inconvénient mécanique d'être l'axe d'inertie moyenne conduisant à un spin instable. A tester?
- Autour de Y, qui se rapprocherait plus d'un "mode moulin à vent", sauf que le vent n'est pas de face. Le choix de Y pourrait présenter l'inconvénient de rester fixe en repère inertiel, alors que le méridien du soleil dérive de presque 1°/ jour, on verra plus loin que ce n'est pas un souci!!!
Le problème du masque radio subsiste.
- Autour de Z, en mode barbecue. Les antennes sont très bien orientées, du moins au début, car Z pourrait rester inertiellement fixe. Le spin est à priori stable, car Z est l'axe d'inertie minimale. La matrice n'étant pas diagonale et les conditions de mise en survie non parfaites, une petite nutation parasite pourrait subsister. Reste à voir la production d'énergie. Sera-t-elle suffisante?
NB : Dans tous les cas de mise en spin, la normale décrira sensiblement un cône d'axe fixe Zo en repère inertiel. Zo est en l'absence de SCAO la direction de Z au moment de la mise en spin. Ceci a pour conséquence que Zo restant quasiment fixe en repère inertiel, les antennes ont un plan parallèle au sol, mais seulement à la latitude où se trouvait le satellite au moment de la mise en spin. Il faut donc soigneusement choisir
Comparaison des puissances :
Notations :
- J jour julien fractionnaire du passage au nœud ascendant. J conditionne la position du soleil en déclinaison, -23°.5 au solstice d'hiver et + 23°.5 à celui d'été.
- t temps orbital écoulé à partir de ce passage au nœud ascendant, la date julienne au moment du calcul est donc Date = J + t.
- Pmax puissance instantanée maximum du générateur, lorsque les rayons sont normaux au plan des panneaux. Pmax = 18 W
- P puissance à la Date correspondant au temps t. P = Pmax cos(a) où a(J,t) est l'incidence. Sur une période seule, on pourra admettre que l'angle ne dépend que du temps orbital et non du jour J ==> a = a(J,t) = a(t), ce qui revient à supposer que sur une période de 101 mn l'unitaire soleil ne change pas.
- TE1(J) = valeur de t lors de l'entrée en éclipse, TE2(J) valeur de t en sortie d'éclipse. Ces 2 temps sont fonctions de J.
I CALCUL DES PÉRIODES D'ÉCLIPSE :
1°) Mise en évidence d'une situation d'éclipse :
Un
satellite peut se
trouver en situation où la terre masque le soleil. Il existe alors des
périodes d'ÉCLIPSE DE SOLEIL. La production d'énergie est donc stoppée,
imposant un stockage de secours à l'aide de batteries pour une alimentation
minimale.
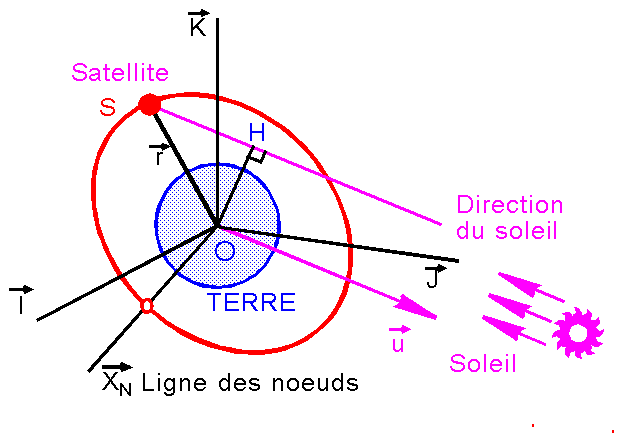
H désigne le point projection du
centre de la terre O sur la direction, d'unitaire u, partant du satellite vers
le Soleil.
Nous
dirons que le satellite S est en éclipse si la longueur TH est inférieure au
rayon terrestre
et si le satellite n'est pas devant la Terre.
Ceci se traduit très simplement,
le lecteur y réfléchira, à l'aide des 2 vecteurs ci-dessous aisément
calculables dans la base du repère IJK associé à J2000.
Unitaire de la direction du soleil,
le vecteur
![]()
Rayon vecteur du satellite, le
vecteur
![]()
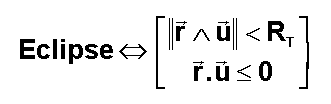
2°) Création d'une fonction eclipse.m sous Matlab : ( La retrouver )
Cette fonction dépend en plus des caractéristiques orbitales de:
- J date julienne au nœud ascendant
- t le temps orbital mesuré depuis le passage au nœud ascendant
- H heure locale au nœud ascendant ( forme décimale 21 h 30 mn => H = 21.5 )
Elle renvoie 0 ou 1 : => 0 en éclipse ou => 1 en visibilité.
Ceci nous permettra d'exprimer la puissance instantanée des panneaux solaires sous la forme
P (J,t) = Pmax*cos(a)*eclipse(J, H, t)
Voir en annexe la vérification de la fonction :
NB : En plus du problème d'éclipse, il faudra encore vérifier que hors éclipse, l'incidence des rayons solaires est inférieure à 90°.
cosa > 0
3°) Calcul de la fonction dans le cas restrictif d'une orbite héliosynchrone:
Il n'est question ici que de savoir si le satellite est ou n'est pas dans le cylindre d'ombre créé par la terre qui intercepte les rayons solaires.
a) Repérage du soleil et du satellite :
Une grande précision n'est pas nécessaire. Deux angles sont utiles :
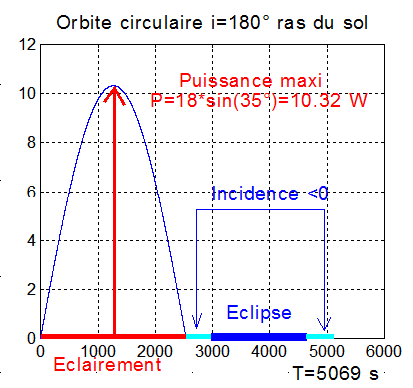
- q angle entre Xn et Xs, cet angle est donné par l'heure au nœud ascendant N. q = 90°+15°*( 12 - H ) = -142°.5, mesuré autour de Zn
- d la déclinaison, donnée par exemple par une formule approchée suffisante( formule de Fletcher ) où J est le numéro du jour de l'année. Il existe évidemment de nombreuses autres relations plus ou moins précises.
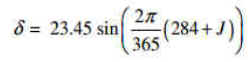
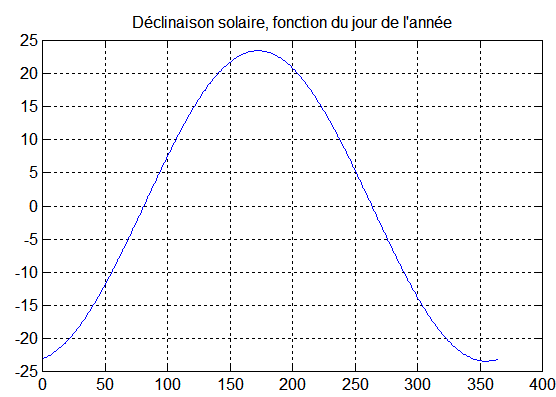
Pour le satellite en orbite circulaire seul l'angle polaire est utile ( avec la convention du temps 0 à l'équateur )
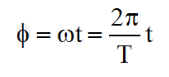
Ci-dessous, un exemple simple ( pour vérification ):
b) Calculs :
Les calculs se font dans le repère Xn Yn Zn, dans lequel soleil et orbite restent en configuration invariable, grâce à l'héliosynchronisme. Us est l'unitaire de la direction satellite-Soleil .
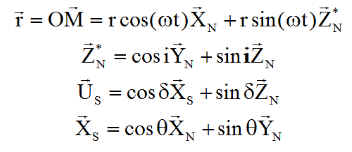
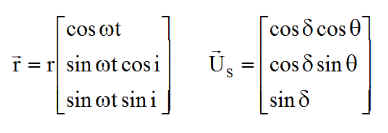
Ci-après la fonction eclipse.m que vaut 1 hors éclipse et 0 en éclipse.
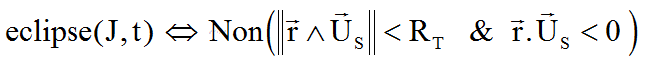
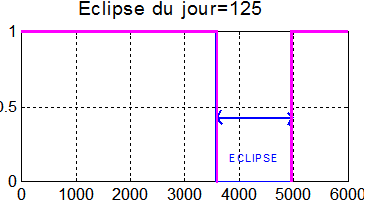
Exécution de eclipse.m pour le jour J=125 de l'année civile
orbite héliosynchrone 817 km, H=18 h
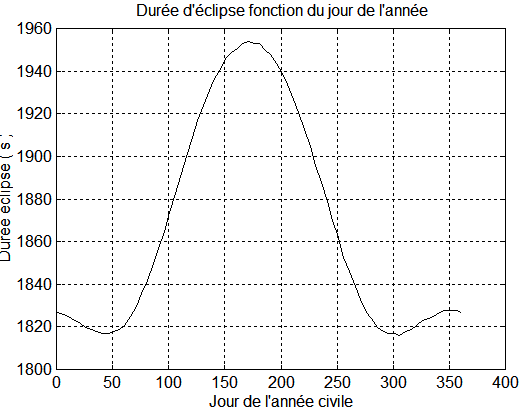
b) Calcul de la répartition des temps d'éclipse sur une année :
C'est l'objet du programme t_eclips.m initialisée par energdat.m ( Retrouver les deux )
Résultat donné ci-dessous. On constate que les temps d'éclipse oscillent entre 30 mn et 32-33 mn, par orbite de 6074 secondes, soit 101 mn. La moyenne est de l'ordre de 31,5 mn.
III MISE EN SPIN AUTOUR DE Y ( mode Moulin à vent ) :
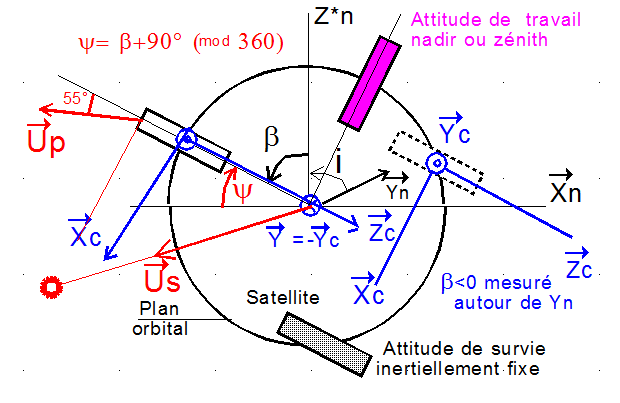
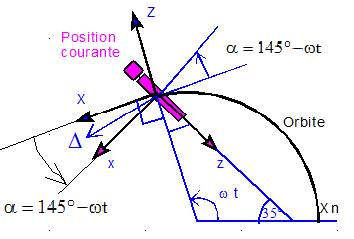
La figure ci-dessous est réalisée dans les conditions d'héliosynchronisme parfait, où les perturbations n'affectent pas la dérivée de la longitude vernale W du satellite. Donc, la configuration Soleil - Orbite est invariable dans le temps. XN YN ZN est le repère associé à l'orbite avec XN au nœud ascendant et ZN direction du nord.
S est la direction du soleil d'unitaire Us. Pour l'instant, il n'est pas question d'éclipse.
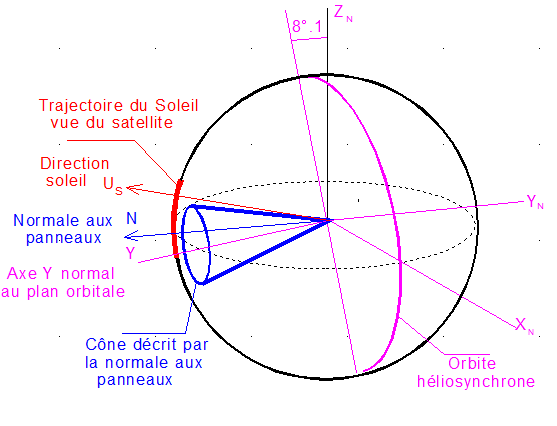
Le soleil parcourt donc un arc de cercle, fixe par rapport à la trajectoire, d'amplitude 23 ° 5 de part et d'autre de l'équateur. L'heure locale étant H = 21 h 30, l'angle de XN avec S est q = 15°*(12 - H ) = -142°.5
La normale N aux panneaux fait un angle de 35 ° avec l'axe Y normal au plan orbital, donc légèrement incliné de 8°.7 sous l'équateur. Le spin autour de l'axe Y fait décrire à N un cône d'axe Y et de demi ouverture 35°. Il est figuré en bleu sur le dessin.
Pour H=21 h 30, on notera que l'arc rouge et le cône bleu n'ont pas de partie commune, ce qui signifie que le soleil n'est jamais normal aux panneaux solaires et que donc la puissance maximum Pmax n'est jamais atteinte.
Que se passerait-il si le mode survie de spin autour de Y était activé?
Le satellite est mis en spin autour d'une direction Yo qui est la normale au plan orbital au moment de l'opération. En l'absence de contrôle SCAO, cet axe reste fixe (aux précessions près dues aux perturbations et au fait que l'axe d'inertie n'est pas exactement principal). Donc le cône bleu est quasiment figé.
Nous savons qu'avec l'héliosynchronisme, la dérive du plan orbital autour de ZN est identique au mouvement du plan méridien du soleil autour de ZN. Donc mouvement de l'arc rouge d'Ouest en Est dans le repère absolu. Le soleil ( arc rouge ) vient donc vers le cône (bleu), ce qui ne peut que faire croître la puissance reçue.
En somme, si lors de la première orbite, avec le satellite "spinné", l'énergie récupérée est acceptable, elle le sera de plus en plus même sur une durée de plus de 2 mois.
1°) L'éclairement est-il suffisant? Comment en juger?
On suppose pour l'agrément du calcul ( ce qui ne change rien au résultat ), que lorsque le satellite survole l'équateur à t = 0 s, la normale Np aux panneaux est en position normale ( notée Np0 ) et que le spin à vitesse Wspin, autour de Y, commence à cet instant.
La figure montre la normale N après rotation de l'angle a = Wspin*t autour de Y, rotation à la vitesse de spin Wspin. Elle est décomposée en OH et HN, avec OH porté par Y, HN porté par V décomposé sur Xn et Z*n.
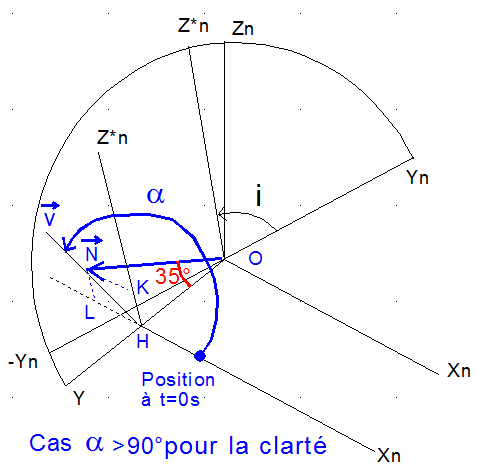
La normale des panneaux "spinnés" est, le lecteur se convaincra des calculs:
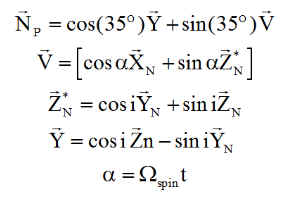
NB : La normale NP0 aux panneaux lors de l'orbite normale, s'obtient simplement en considérant qu'elle est "spinnée" autour de Y à la vitesse angulaire orbitale w0 On peut alors calculer les énergies reçues sur un tour d'orbite, soit en situation normale soit en survie. Dans les 2 cas il faut réunir des conditions d'éclairement correctes, à savoir, un satellite en visibilité du soleil et une incidence sur les panneaux entre 0 et 90°.
![]()
Nous traduisons ceci par deux constantes booléennes Kn et Ks pour le régime normal et le mode survie, prenant évidemment les valeurs 1 ou 0.
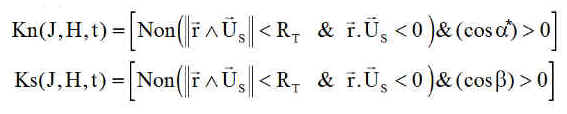
NB : on peut tester le signe de la puissance et la prendre nulle lorsqu'elle est négative.
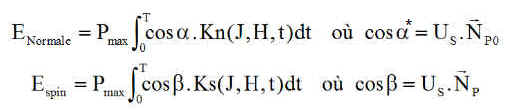
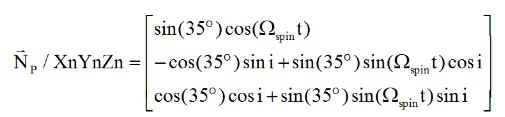
NB : On notera qu'il est aisé de passer de Np à Npo en changeant Wspin en wo, la rotation orbitale.
1 ) Energie produite au cours de l'année :
Le satellite est supposé être dans son mode nominal en pointage nadir stabilisé avec l'axe satellite de tangage - y = Ysat aligné sur Y et Zsat sur - Z.
Résultat du programme C:/CASASURV/energies/enerJour.m ( Le retrouver ) qui donne en sortie, pour H donnée et une puissance panneaux théorique de 18 Watts, l'énergie maximale récupérée dans le jour J de l'année civile. Par division avec la période orbitale de 6074 s, on obtient la puissance moyenne: correspondante.
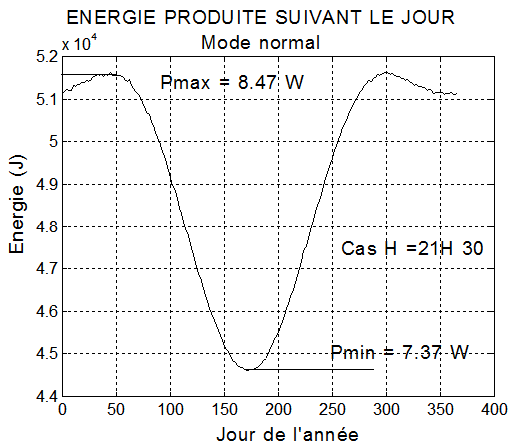
On constate, sous régulation fine de pointage nadir en continu, une production à puissance moyenne variant entre 7.4 et 8.5 W/jour.
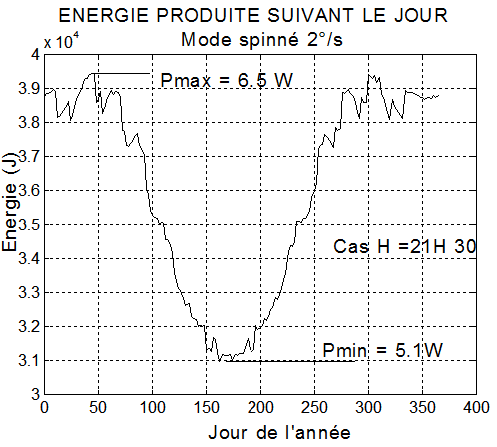
Pour le mode "spinné" la production d'énergie est inférieure à celle du mode normal, la puissance moyenne variant entre 5.1 et 6.5 W/jour.
Conclusion : ce mode ne semble pas adapté à une survie, car sa production énergétique est trop basse.
2 )Exemple aux environs du solstice d'été ( jour 183 ) :
Mise en spin, le 2 juillet, à t = 0 secondes, au dessus de l'équateur, au nœud ascendant, à la vitesse de 10°/s, autour de Y qui coïncide alors avec -Xn.
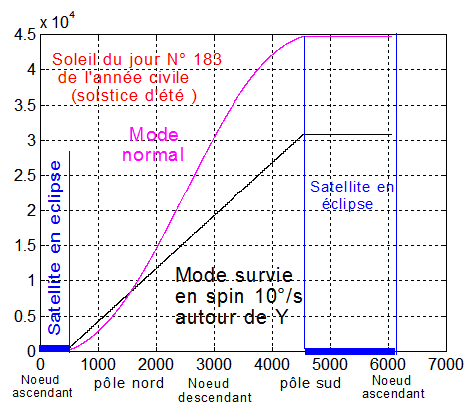
Sur une période près du solstice d'été:
- Les 2 modes sont en éclipse plus d'une demi heure.
- Les 2 modes génèrent une énergie de 45000 Joules et 30000 joules, sur une période de 6074 s, soit une puissance moyenne de 7.5 W en normal et 5 W en mode "spinné"
NB 1 : L'essai de plusieurs valeurs de la vitesse de spin montre qu'elle n'a pas d'influence notable sur l'éclairement et la production d'énergie. Ce qui parait logique compte tenu du fait que le spin, s'il est parfait, fait décrire à la normale aux panneaux, un cône d'axe Y toujours positionné de la même façon par rapport à la position du soleil, du moins pour une seule orbite et un jour donné. Donc, si le spin est doublé, les panneaux passent 2 fois plus vite sous les rayons du soleil, mais avec les 2 tours, le temps d'éclairement sera le même.
Cette réflexion va nous faciliter le travail de III
NB 1 : Cas où le mode survie devrait durer plus longtemps que prévu:
Plusieurs considérations s'imposent :
- Tout d'abord avec un spin idéal, si tant est que les perturbations ne le dérangent pas trop, l'axe de spin va rester fixe en repère inertiel. Notons le Y0, comme l'axe Y à l'instant de la mise en spin. Par contre le plan méridien du soleil, ne manquera pas de précessionner à 1°/jour, autour de l'axe des pôles, d'Ouest en Est.
Ce qui, pour l'heure H = 21 h 30, est favorable au rapprochement du plan méridien solaire et de l'axe du cône du mouvement de la normale aux panneaux. La puissance ne peut qu'augmenter. Ceci pendant près de 35 jours, pour ensemble retrouver le niveau initial en décroissant pendant 35 jours, puisque l'ouverture du cône est 70°.
- Pendant ce temps de 3 mois environ, la déclinaison du soleil va varier, avec des conséquences plus ou moins importantes suivant la date
- Si c'est début avril, le soleil monte au solstice d'été, puis redescend et retrouve sa position d'avril. La variation de déclinaison est faible.
- Si c'est une date anniversaire d'un solstice ou d'un équinoxe, la variation de déclinaison sera notable sur 3 mois.
REMARQUE SUR LE MODE "BARBECUE" :
On aurait pu imaginer une mise en spin autour de X, en mode dit barbecue. Mais alors, la puissance reçue est moins de 50% de puissance théorique maximale qui a été appréciée vers 12 W. Donc ce mode doit être abandonné.
CONFIRMATION DE LA PUISSANCE PAR LA RÉGULATION DE LAURENS :
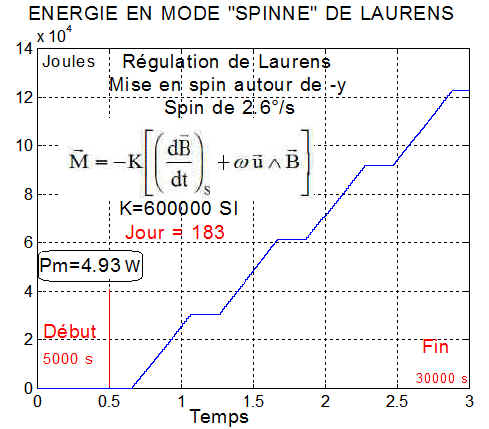
On retrouve la puissance en mode "spinné" calculée plus haut pour le jour 183, soit sensiblement Pm = 5 W, les parties horizontales correspondent aux éclipses au sens large ( éclipse ou éclairement de la face opposée aux panneaux )
IV MODE SURVIE PRIVILÉGIANT L'ÉNERGIE?
REMARQUE PRÉLIMINAIRE :
Une idée qui vient naturellement à l'esprit, pour optimiser la production d'énergie par les panneaux solaires, est d'essayer de "spinner" le satellite autour de la direction de la normale aux panneaux et de faire précessionner cette direction vers le soleil. Après maints essais, beaucoup de surprises et d'interrogations, cette solution n'a pas abouti, la situation est instable. Voir l'étude dédiée
LE CHOIX ACTUEL :
1°) LOI DE CONTRÔLE DU SPIN EN ÉCLIPSE :
Ce qui suit est simplement une mise en forme d'un contrôle déjà testé et présenté par M STEYN dans une publication en PDF . Restera à voir si l'attitude est compatible avec les télécommunications sol.
Le contrôle du satellite en détumbling est assuré par le moment magnétique My qui travaille à réduire l'angle b entre le vecteur champ magnétique B et l'axe y du satellite. L'étude a déjà été faite voir page dédiée.
Un mode survie est mis en place avec 2 lois distinctes utilisées séparément:
En éclipse, la loi ci-dessous assure le contrôle du spin autour de y
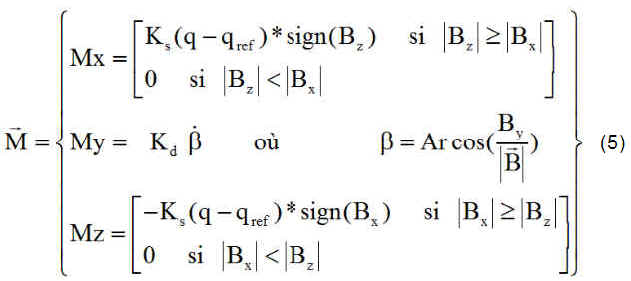
Hors éclipse, est privilégiée la production d'énergie par une mise en précession de l'axe de spin vers le soleil. C'est la régulation détaillée ci-dessous.
Notations :
S = [Sx Sy Sz]T = unitaire du soleil en axes satellite. On pourra le retrouver ailleurs comme Us
s = Angle entre l'unitaire du soleil et l'axe de tangage y du satellite
Hy = moment angulaire vectoriel du satellite autour de y, Hy=It*q_ref
Kp = gain du contrôle de la précession
2°) LOI DE CONTRÔLE DE LA PRÉCESSION VERS LE SOLEIL ( Logique de M STEYN ): Cas du microsatellite SumbandilaSAT, où les panneaux sont sur la face y+.
Pour lequel, on souhaite pour les périodes hors éclipse, augmenter la puissance du générateur.
Il faut donc rapprocher l'axe y ( normale au plan porteur des cellules solaires ) du plan méridien du soleil et mieux encore de la direction S du soleil. Le dessin est un schéma de principe pour SumbandilaSAT , notre satellite ayant lui une disposition différente des panneaux.
ATTENTION : Normalement, la manœuvre la plus efficace consisterait à rapprocher la normale aux panneaux N de la direction S du soleil, car pour notre satellite le plan des panneaux n'est pas orienté par y ou -y. Dans l'immédiat, on traite le cas des panneaux de SumbandilaSAT .
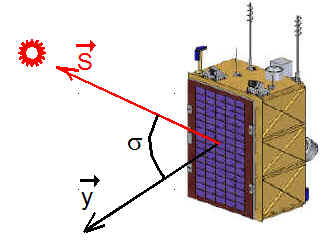
a) La précession W à créer doit donc être portée par le produit vectoriel de y et de S ( qui rapproche y de S ). De la forme
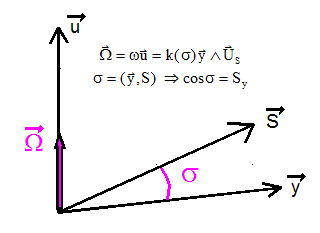
On peut par exemple choisir une rotation d'autant plus importante que l'angle s est grand. En somme une loi proportionnelle.:
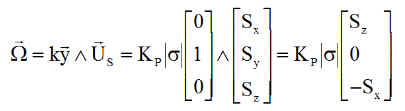
avec le décalage s calculé plutôt avec la tangente ( qui donne moins de souci à inverser que le cosinus )
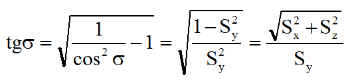
NB : en pratique la mesure de la précession peut être:
![]()
b) Calcul du moment magnétique de commande :
C est le couple de commande. La précession est supposée petite devant le spin. Le satellite est "spinné" autour de y et son moment cinétique a pour partie principale H=Hy sur y, constante, donc la dérivée du moment cinétique est quasiment nulle ce qui conduit à écrire:
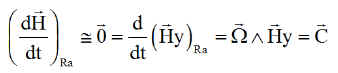
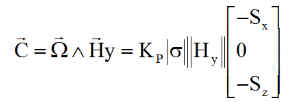
En gyroscopie, on dit que le couple gyroscopique "contre" le couple de commande, en créant une précession et donc un couple gyroscopique secondaire. C'est la précession espérée.
Si M est le moment magnétique requis pour créer C, alors
![]()
NB : il sera inutile ici d'optimiser le moment magnétique, puisqu'il et normal à B
Conclusion: le moment magnétique de commande est
|
|
REMARQUE IMPORTANTE : En pratique cette régulation fait précessionner l'axe de spin vers toute direction D liée ou non au soleil. Elle est donc utile pour une reconfiguration d'attitude, dans d'autres applications.
APPLICATION POUR NOUS: Pour notre nanosatellite, les panneaux sont du côté de la face y- donc la précession doit amener l'axe -y sur S ou mieux y vers la direction D = - S. Le moment magnétique M est l'opposé de celui écrit plus haut
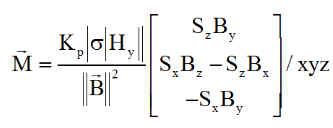
Calcul de l'unitaire soleil en axes orbitaux XYZ :
Cette connaissance est nécessaire pour le calcul M, avec s et Sx Sy Sz. Le calcul est un changement de base ( voir détails en annexe 2 )
Donnant les composantes de l'unitaire soleil dans XYZ
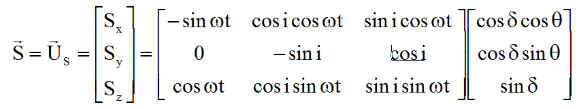
NB : Calculs testés par transformations directes et inverses, normes des vecteurs et déterminant de matrice fonction SunitXYZ.m ( La retrouver )
3°) RÉSULTATS DE LA COMMANDE MIXTE DE M STEYN :
Rappelons qu'il y a alternance de 2 régulations:
- à partir d'un temps à déterminer, pour moi 8000 secondes, le "tumbling" est terminé et la mise en spin est effectuée.
- alternent alors : la mise en précession vers le soleil hors éclipse et le retour à la mise en spin en éclipse.
A - PREMIERE SIMULATION: c:/casasurv/surv_sim.m initialisée par surv_dat.m ( Retrouver les fichiers )
Elle est totale, depuis l'injection à des vitesses angulaires de l'ordre de 15°/s. "Détumbling", puis mise en spin à w_spin = -3.2°/s à 1500 s. Mise en place des séquences alternées au temps 8000 secondes, jusqu'à la fin de la simulation à 20000 secondes; jour = 81 correspondant à l'équinoxe de printemps.
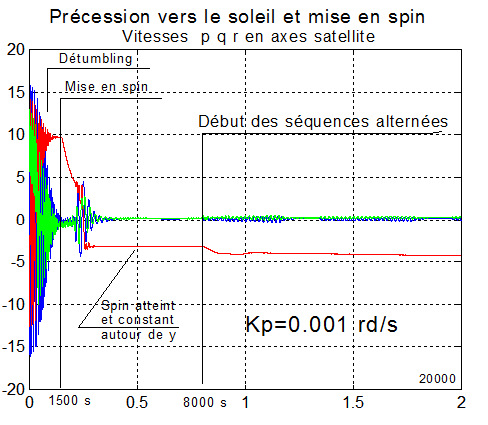
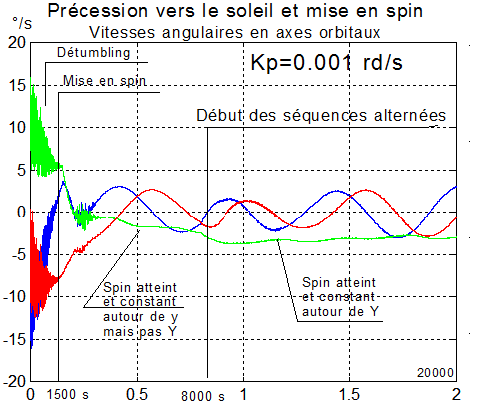
Commentaire : le spin est assez bien respecté, les vitesses angulaires transverses modérées.
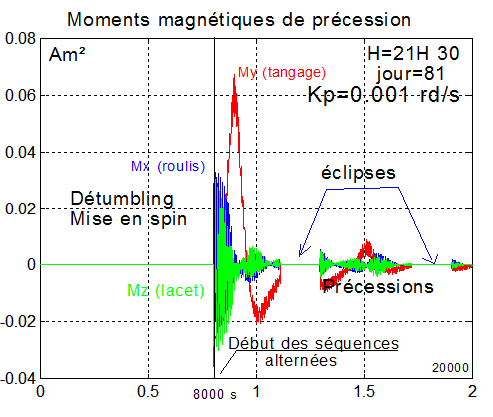
Commentaires :
- les moments magnétiques sur les 3 axes ne dépassent pas 0.06 Am², soit un fonctionnement à 30% des capacités maximales.
- les durées d'éclipse apparaissent clairement, de l'ordre de 1800 à 1950 secondes, conformes aux durées déjà calculées plus haut. De 8000 s à 20000 s, il s'écoule 2 orbites et donc 2 éclipses ( normal ).
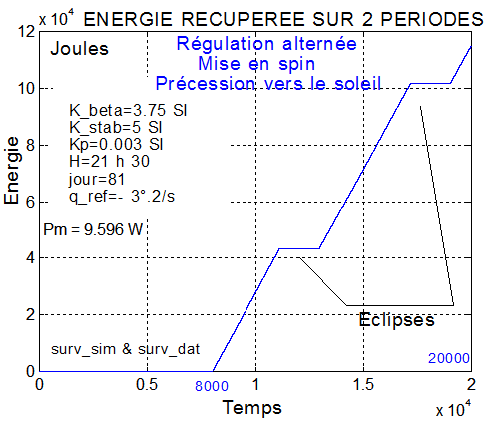
Commentaire : Les 2 courbes, l'une avec l'inversion de la tangente et l'autre du cosinus, montrent nettement une convergence de l'axe y vers la direction du soleil en 20000 s.
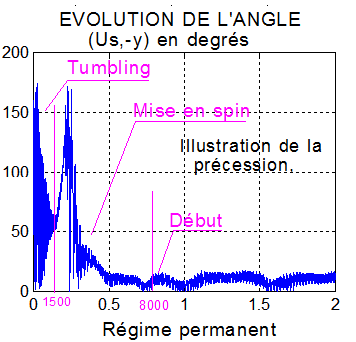
Alors faut-il s'approcher au maximum ou faire un compromis en diminuant le gain de la régulation précession au profit de celui du contrôle du spin?
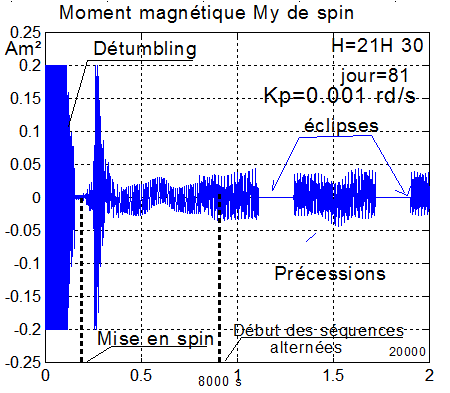
Commentaire : Ci-dessus le plus grand des moments magnétiques de la régulation de spin, soit My. Sa valeur ne dépasse pas 0.05 Am², donc le quart du maximum autorisé 0.2 Am².
On peut donc conclure que le SCAO ne demandera pas plus du tiers des performances des magnétocoupleurs.
B - AUTRES ESSAIS:
1 - Avec un spin choisi à -3.2°/s, Kp=0.0001 réduit d'un facteur 10 par au cas précédent. La précession permet de s'approcher jusqu'à 40° de l'axe du soleil, du moins sur 2000 s.
2 - Avec un spin choisi à -1°/s, Kp=0.0001. La précession est parfaitement efficace , les moments magnétiques sont de l'ordre de 0.001 Am².
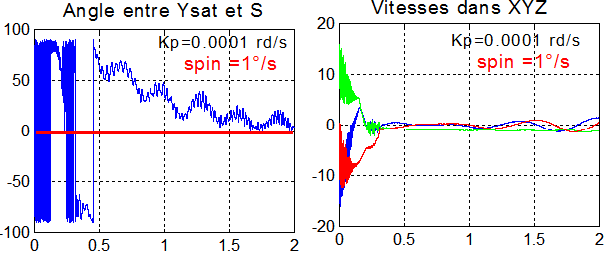
C - PRODUCTION D'ÉNERGIE EN RÉGIME MIXTE:
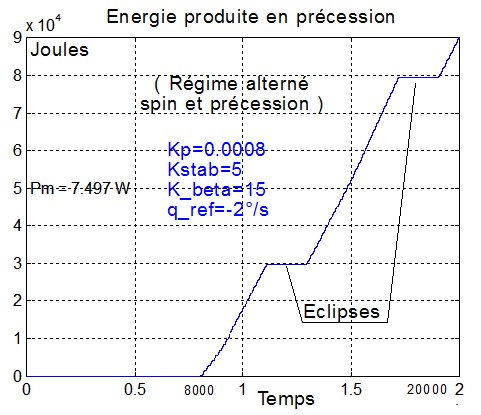
Energie 90000 W Kp=0.0008
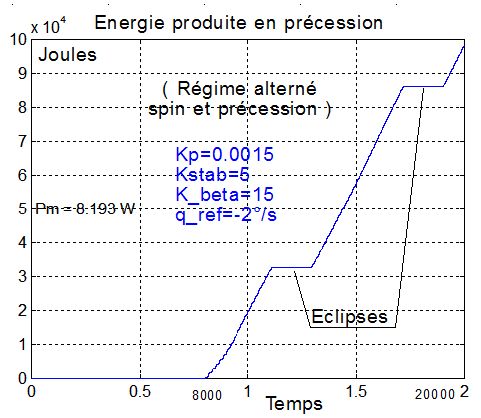
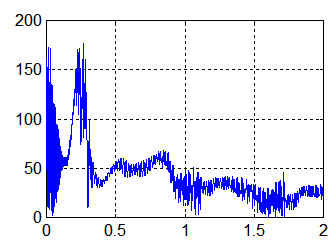
Angle entre -Us et y , Kp=0.0015
Commentaires : divers essais montrent que l'augmentation du gain Kp de précession s'accompagne de :
- Une augmentation de la puissance moyenne 7.5 w pour Kp=0.0008, 8.2 w pour Kp=0.0015 et 8.4 W pour Kp=0.002 etc...
- Une convergence plus nette de y vers -Us.
- Une augmentation des vitesses angulaires transverses au spin.
- Une augmentation en proportion des moments magnétiques nécessaires sans pour cela dépasser 0.04 Am².
Deux cas concernant la régulation mixte mise en spin en éclipse et précession vers le soleil hors éclipse.
|
CAS1 : sur 40000 secondes, q_ref = -2°/s K_beta = 3.75 K_stab = 5 Kp = 0.0028 |
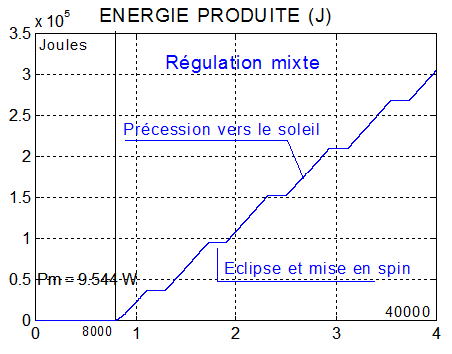
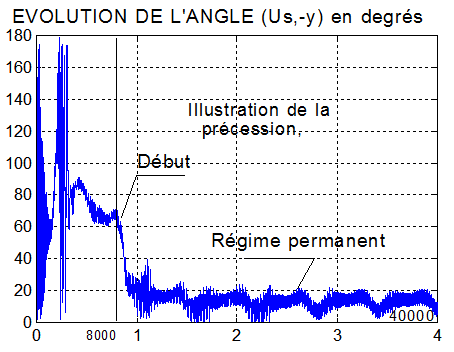
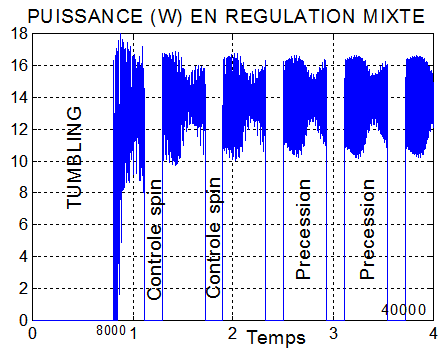
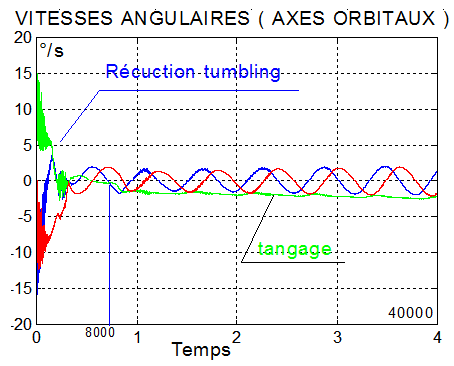
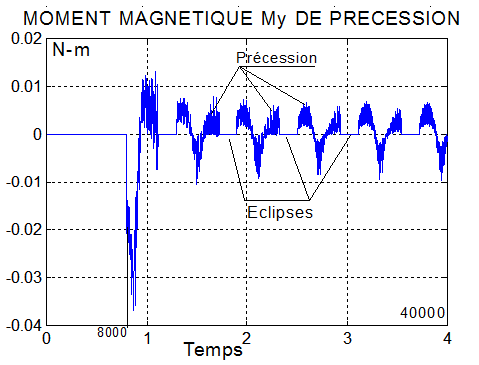
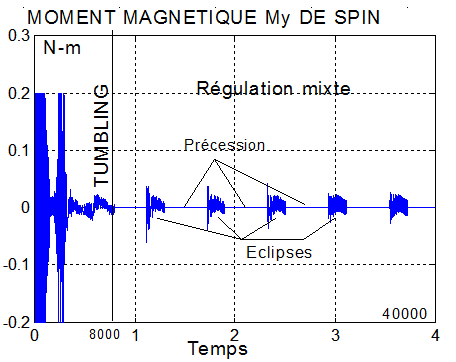
|
CAS1 : sur 40000 secondes, q_ref = -6°/s K_beta = 3.75 K_stab = 5 Kp = 0.0028 ( Avec les mêmes annotations qu'au dessus) |
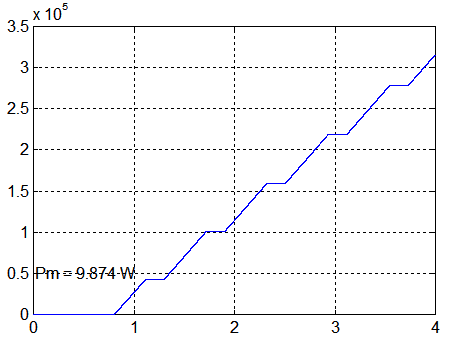
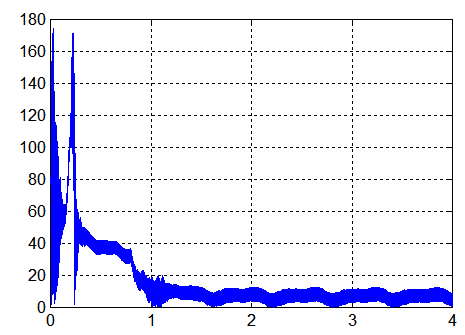
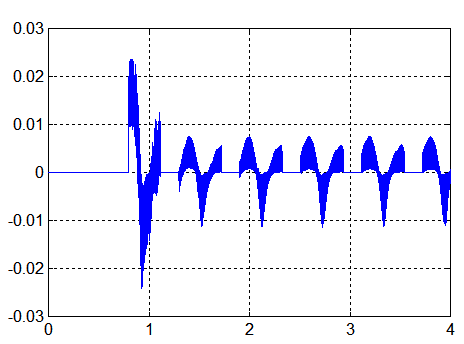
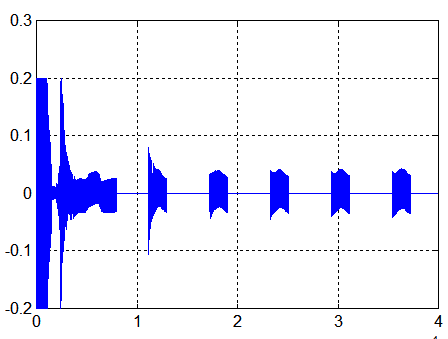
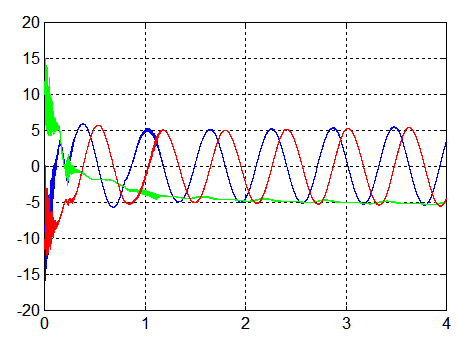
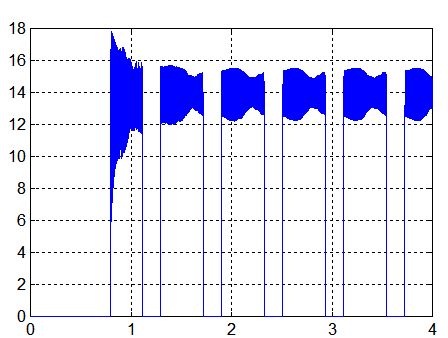
Commentaires :
- Le spin plus fort du deuxième cas améliore la performance énergétique, mais amène à des vitesses angulaires transversales plus grandes ( 5°/s )
- Une production continue à la puissance moyenne de 9.5 Watts devrait convenir pour un mode survie
- De plus, il se pourrait que les équipements embarqués( propagateur d'orbite sur TLE+magnétomètres+modèle IGRF de champ magnétique redondant en localisation) devraient permettre la régulation mixte sans recours à des senseurs solaires.
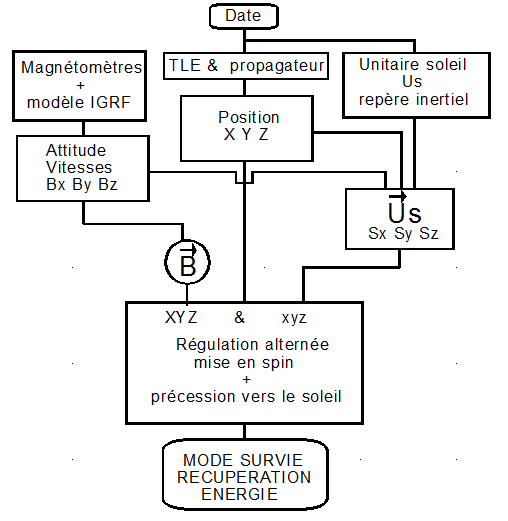
VI SURVIE ET POINTAGE DU SOLEIL ( Méthode de Laurens ) : Voir la théorie de Laurens
L'idée de base est de rapprocher l'axe y du satellite de la direction du soleil Us et si possible l'aligner sur lui.
Simulation C:/casasurv/laurspin/survlaur.m ( Retrouver les fichiers )
1°) Loi de commande :
Cette loi consiste à définir un repère de consigne, noté Rc = ( Xc Yc Zc , fixe ou mobile ) et une régulation amenant le repère satellite R = ( x y z ) en coïncidence avec Rc.
La méthode, inventée par Monsieur Laurens de chez Astrium, consiste à prendre pour vecteur champ magnétique de consigne le vecteur champ magnétique Bc calculé dans Rc et de le transposer dans R, en gardant les mêmes composantes dans xyz.
La régulation consiste alors à amener B sur Bc. Pour ce faire, avec des magnétocoupleurs sur chaque axe, l'idée géniale de Philippe LAURENS est de poser comme moment magnétique de la régulation :
![]()
Pour être plus clair, on aurait pu dire qu'il pose un moment magnétique proportionnel à la différence des champs et qu'au final, économe en calculs, il omet B qui disparaît dans le produit vectoriel:
![]()
Le couple magnétique tend à amener B sur Bc ou encore Bc sur B. C'est l'effet "boussole".
2°) Calcul de Bc/xyz :
La direction unitaire du soleil, à toute date , est supposée connue :
- Soit par des senseurs solaires à bord, dans ces conditions Us est connu dans le repère satellite R = xyz
- Soit par un propagateur de trajectoire embarqué et dans ce cas là, Us est connu dans le repère orbital Ro = XYZ
- Soit par une restitution d'attitude associée à un modèle IGRF de champ magnétique et à la date, dans ce cas là Us est connu dans R et Ro
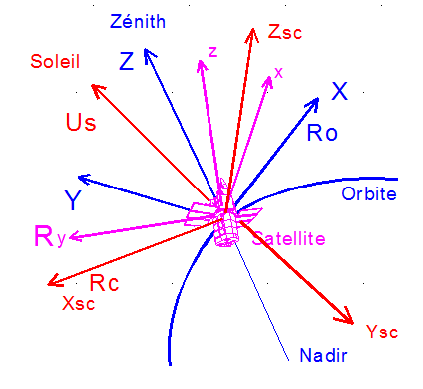
a) Matrice de passage de Rc à Ro :
On introduit un repère Rc dit de consigne Rc = Xsc Ysc Zsc , défini en liaison avec le soleil ( sauf cas particulier d'une orbite H = 18 h, l'axe Y ne pointe jamais le soleil ) :
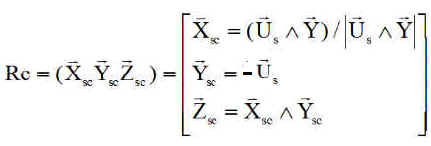
La connaissance conjointe de Us = (SX SY SZ ) dans XYZ permet le calcul de la matrice de passage P(Rc=>R0) de Rc à R0. Le lecteur démontrera que cette matrice vaut :
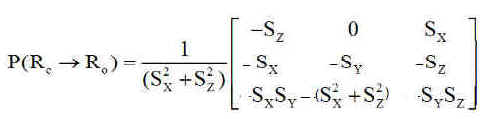
NB : On peut vérifier que son déterminant vaut 1
b) Matrice du vecteur Bc dans Rc :
Le vecteur champ magnétique B est connu en axes orbitaux, de matrice B = [ BX BY BZ]T , ce qui donne les composantes de B en repère de consigne Rc
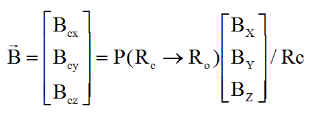
c) Matrice du vecteur Bc dans R :
L'invention de M Laurens est de garder les composantes calculées ci-dessus, dans le repère satellite, comme composantes de consigne pour B.

3°) Outils de la simulation ( écrits sous Matlab version 1990 ):
a) Fonctions :
- soleil.m : fonction du temps, retourne 0 ou 1 en éclipse ou hors éclipse. Paramètres H (heure solaire) jour ( N° du jour de l'année )
- SunitXYZ.m : fonction du temps, retourne L'unitaire du soleil, dans le repère orbital Ro = ( XYZ ). Paramètres H (heure solaire) jour ( N° du jour de l'année )
- unitSxyz.m : fonction du temps et qu quaternion d'attitude, retourne L'unitaire du soleil, dans le repère satellite R = ( xyz ). Paramètres H (heure solaire) jour ( N° du jour de l'année )
- Unit_Sat.m : retourne l'unitaire soleil dans le repère satellite, ceci pour les calculs d'énergie des panneaux solaires. Le vecteur d'entrée est :
u est le vecteur
d'entrée à 10 composantes:
u(1:3) = Us unitaire soleil en repère orbital R0
u(4:6) =Omega rotation absolue en axes satellite R
u(7;10) est le quaternion d'attitude du satellite xyz / XYZ repère
orbital
- P_Rc_2_R.m : retourne la matrice de passage du repère de consigne Rc au repère satellite R
La variable d'entrée est
composée de 8 termes:
u(1) le temps u de la simulation
u(2:4) =[p q r] le vecteur rotation instantanée du satellite par rapport au
repère orbital, exprimé en axes satellite.
u(5:8) le quaternion d'attitude de R satellite xyz / XYZ
- Bc_sur_R.m : retourne les composantes du vecteur de consigne Bc dans les axes satellite
La variable d'entrée est
composée de 4 termes:
u(1) le temps u de la simulation
u(2:4) le vecteur champ magnétique en repère orbital
- Mat_Rc2R.m : retourne la matrice de passage de Rc à R. Le vecteur d'entrée est :
La variable d'entrée est
composée de 8 termes:
u(1) le temps u de la simulation
u(2:4) =[p q r] le vecteur rotation instantanée du satellite par rapport au
repère orbital, exprimé en axes satellite.
u(5:8) le quaternion d'attitude de R satellite xyz / XYZ
- verifica.m : programme de vérifications, sur un instant quelconque de la simulation nanosim.m , de tout type de transformation matricielle ou vectorielle : OK
b) Simulation : C:/casasurv/laurspin/survlaur.m
VII TENTATIVE DE MISE EN SPIN AUTOUR DE LA NORMALE AUX PANNEAUX :
Celle avec la technique de Steyn a été un échec. Je la reprends donc avec la régulation de Laurens, qui réalisait le "détumbling" puis la mise en spin autour d'un axe choisi à une vitesse angulaire également choisie, pour comparer les résultats.
C:/casasurv/laurspin/survsiml.m initialisée par surv1dat.m ( Retrouver les fichiers )
Exemple de mise en spin ( méthode de Laurens ) autour d'un axe fixe par rapport au satellite ou encore xyz
On notera les régimes permanents affectés d'une petite oscillation, de période 3000 s moitié de la période orbitale 6000 s,
Ci-dessous le lacet, apparemment très stable ( axe_spin=[0 0 1] )
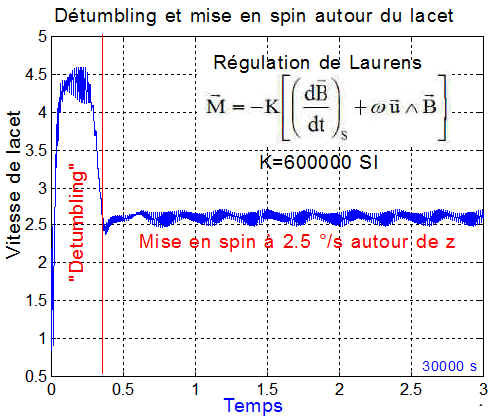
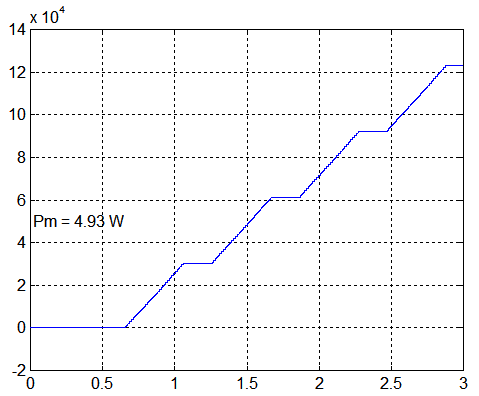
Energie produite ( J ) et puissance moyenne de 5 W
de même que le spin autour du tangage ( axe_spin=[0 1 0] )
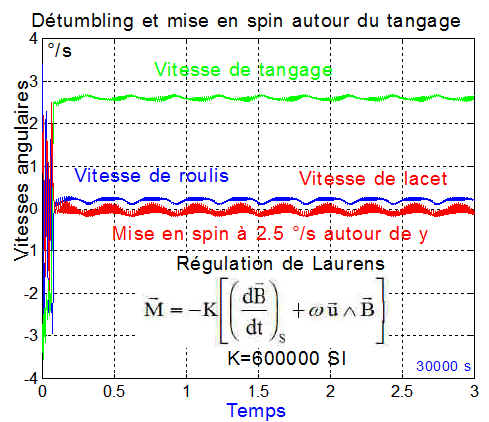
Le spin en roulis tente de s'établir mais est visiblement périodiquement instable ( axe_spin=[1 0 0] ), entraînant par couplage une instabilité sur tous les axes
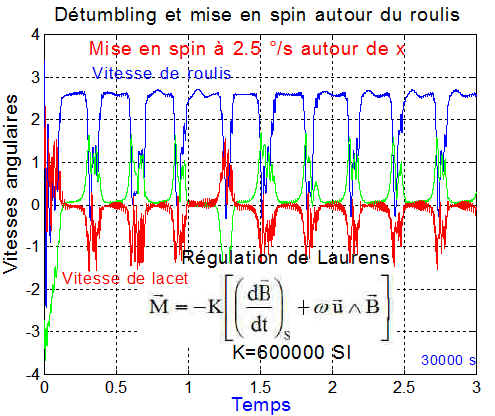
Pour finir et retrouver le problème déjà rencontré avec les techniques de Steyn, voici la mise en spin autour d'une direction parallèle à l'axe des panneaux ==> axe_spin=[0 -cos(35*pi/180) -sin(35*pi/180)];
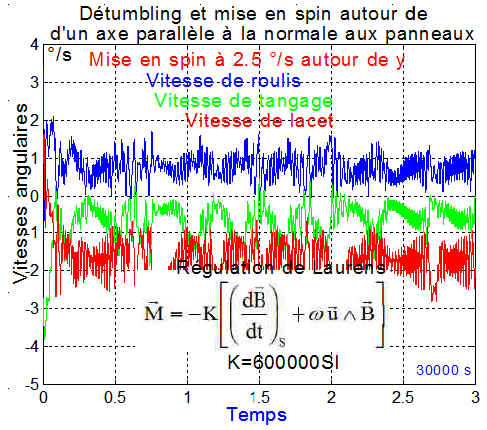
Les vitesses angulaires sont chaotiques
Le tracé de la vitesse angulaire de spin autour de la normale, donne avec la projection adéquate sur l'axe de spin choisi ==> plot(temps,(p*axe_spin(1)+q*axe_spin(2)+r*axe_spin(3))*180/pi)
Nous sommes loin d'un état stable!!!
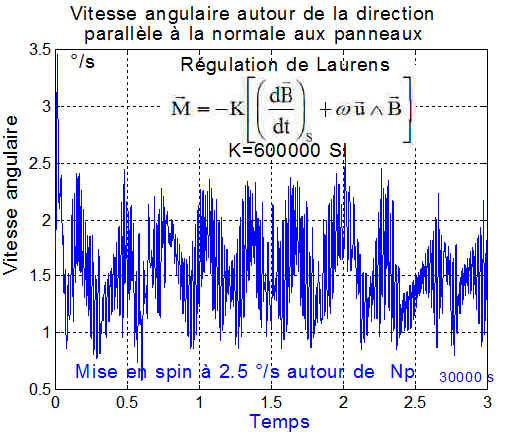
Conclusion : en cause probablement la position moyenne des inerties autour de x et de la parallèle à la normale. Affaire à confirmer!!!
Cette nouvelle simulation totalement indépendante de celle de Steyn, semble confirmer l'impossibilité de "spinner" le satellite autour d'un axe parallèle à la normale aux panneaux. Sauf, bien sûr à revoir la géométrie du satellite!!!
VIII MODE SURVIE PAR MISE EN SPIN AUTOUR DE LA DIRECTION DU SOLEIL :
La mise en spin autour de la normale aux panneaux semble pour moi un échec. Je reprends donc la régulation de Laurens, qui réalisait le "détumbling" puis la mise en spin autour d'un axe choisi à une vitesse angulaire également choisie, pour comparer les résultats. Cette fois, l'axe de spin est l'unitaire soleil. Bien évidemment l'axe de spin satellite est y ou -y suivant le signe du spin.
C:/casasurv/laurspin/SurvSpin.m initialisée par sur2dat.m
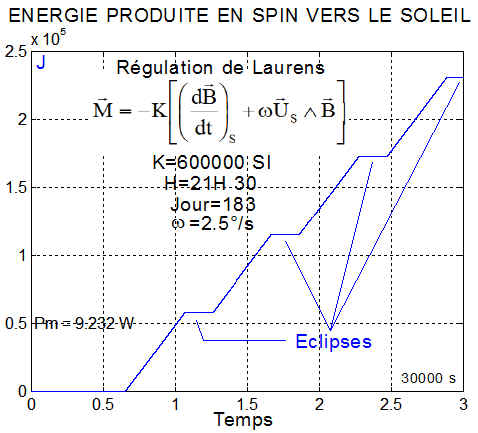
1°) La loi de commande en 2 temps : H=21 h 30, pas de roue, jour=183
a) Premier temps : de 0 à 1500 s, la plus simple des régulations en B-dot, avec K=600000SI
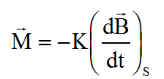
a) Deuxième temps : de 1500 s à 30000 s ( 5 orbites ), la régulation en B-dot complétée par la mise en spin autour de la direction pointant le soleil, avec toujours K=600000SI. La vitesse angulaire de l'exemple est de 2.5 °/s.
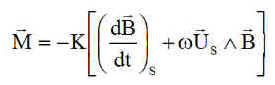
La simulation commence à mesurer l'énergie produite, à parti de 5000 secondes, de manière à avoir un régime stabilisé et une excellente idée de la puissance moyenne.
2°) Les vitesses angulaires :
Une fois amorti le "tumbling" initial ( faible sur l'exemple ), la stabilisation est parfaite. La vitesse de tangage est celle du spin à 2.5°/s en résonance classique avec le champ magnétique terrestre à une période d'environ 3000 secondes, moitié de la période orbitale ( 6074 s ). On note une très petite nutation transversale.
Énergie produite :
Pour le jour 183, la durée des éclipses est de 1955 s par période de 6074 secondes. Rappelons que la normale aux panneaux est inclinée de 35° sur l'axe - y.
Le graphe de l'angle entre l'axe - y et Us direction unitaire du soleil, donne un angle d'environ 6°.
La puissance minimale moyenne sur une orbite, est donc sensiblement
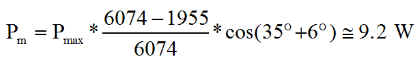
C'est bien la valeur enregistrée après 5000 secondes. Ce niveau d'énergie est tout à fait acceptable.
IX MODE SURVIE PAR STABILISATION QUASI INERTIELLE :
L'idée est de garder le satellite avec l'axe y+ de sens contraire à Y, la roue en spin négatif constant autour du tangage et le satellite inertiellement quasi fixe ( au détail près de la précession de la ligne des nœuds ) dans le plan orbital, de manière à verrouiller l'éclairement solaire tout au long de l'orbite et de l'année. La figure qui suit montre une position simple par rapport aux axes XnYnZn liés à la ligne des nœuds à mi chemin de l'équateur et du pôle Nord. Le plan (x z) du satellite doit rester confondu avec le plan orbital, seul un décalage angulaire fixe et bien étudié va résoudre très simplement le problème de la survie.
1°) Champ de consigne non optimisé pour une survie printemps-été :
C'est, pour commencer et mettre en place une régulation de Laurens, une première approche non optimisée. En effet, comme l'heure locale au nœud ascendant n'est pas 18 h, les unitaires du soleil et de la normale aux panneaux ne sont pas dans le même plan méridien.
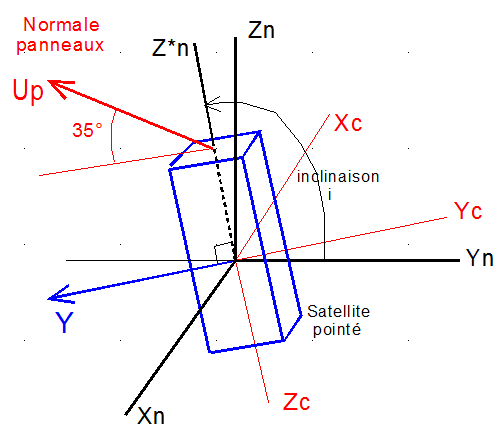
La matrice de passage du repère de consigne XcYcZc au repère nodal XnYnZn est donc:
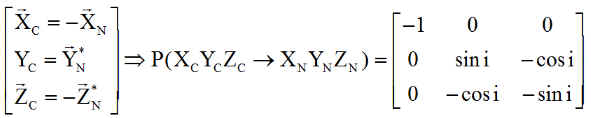
La matrice de changement de base de XYZ à XnYnZn est ( voir en annexes )
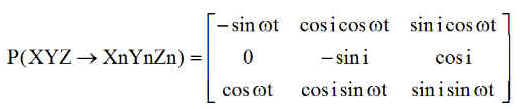
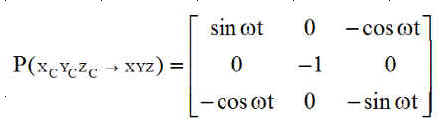
Le champ magnétique en axes orbitaux XYZ est connu ( BX BY BZ ), donc le champ de consigne est
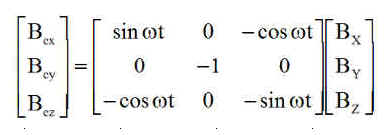
C'est l'objet de la fonction BCXnYnZn.m les composantes seront reportées dans le repère satellite pour constituer la consigne Bc dans xyz.
COMMENTAIRES : Une simulation avec calcul de l'énergie donne, pour le jour 181 de l'année, au solstice d'été, une puissance moyenne de 8.2 W constants avec une excellente stabilité acquise à partir de la position de travail en 6000 secondes. Simulation survfix0.m initialisée par nanodat1.m. On sent cependant bien que l'on peut réduire l'angle des unitaires soleil et panneau, par exemple en rapprochant l'axe z- de la ligne des nœuds. ( Retrouver les fichiers )
2°) Recherche du champ de consigne optimisé pour une survie à l'équinoxe de printemps ou d'automne :
Par rapport au cas précédent, on rajoute un paramètre angulaire, noté b, qui est l'angle de rotation autour de Y*= Yc, faisant passer du repère précédent X* Y* Z* de 1°) au repère de consigne actuel Xc Yc Zc
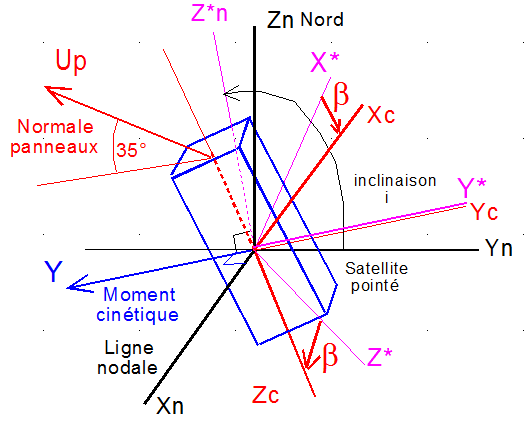
Il suffit de prendre en compte la matrice de passage de XcYcZc à X*Y*Z*
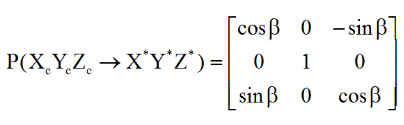
Finalement le champ de consigne est :
|
|
Simulation survfix1.m initialisée par nanodat1.m. L'angle b s'appelle beta_fix dans l'initialisation nanodat1. ( Retrouver les fichiers )
Premier résultat encourageant: Le cas le plus simple pour vérifier la simulation, est de se placer le jour du printemps ( jour=81 ). Ce jour là le soleil est dans le plan équatorial et pour une heure locale de 21H .30, l'angle avec -Yn est de 3.5*15 = 52°.5 ( car l'heure locale est 21 H 30 ).
Le cas optimal pour la normale aux panneaux est pratiquement d'être elle aussi dans le plan équatorial. La configuration exacte qui assure un bon éclairement des panneaux s'obtient pour b = - 90° ( le satellite est alors couché sur la ligne des nœuds avec la face Z+ orientée vers le nœud ascendant :
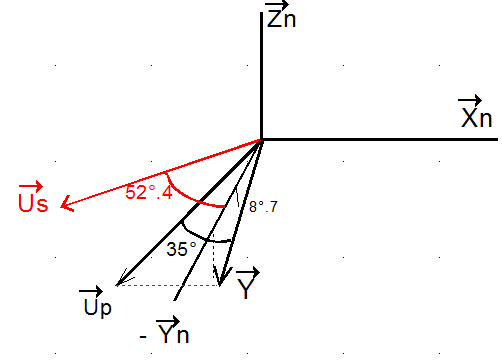
Le produit scalaire de Us et Up ( cosinus de l'incidence ) est
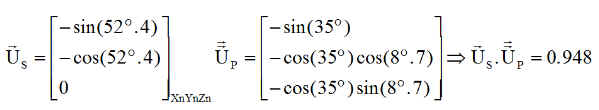
La puissance espérée optimale, compte tenu :
- Qu'elle est constante
- Que le temps d'éclipse est de 1840 s sur une période de 6074 s
- La puissance maximum est de Pmax = 18 W
P = 18*(6074-1840)/6074*0.948 = 11.9 Watts
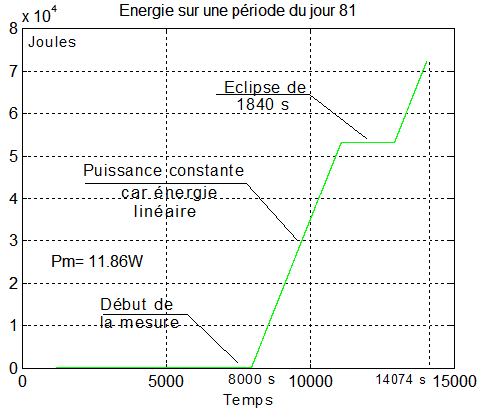
Conclusions :
La confirmation du résultat est irréfutable, démontrant notamment la validité du concept, la précision de la simulation et surtout la validité des calculs matriciels sur lesquels s'appuie une régulation de Laurens vraiment étonnante d'efficacité.
La vitesse de tangage est au final de 1.3 e-5 rd/s assurant une stabilité de 5°/ orbite.
La composante N°3 du quaternion d'attitude de xyz par rapport à XYZ orbital est q3 = 8 e-4, assurant un dépointage de y par rapport à Y de 179°.4, donc à 0.6° du pointage idéal.
La régulation ne demande qu'une roue à vitesse constante, qui peut être lancée en rotation dès la mise en orbite ( Ce sera la cas dans la simulation synthesT.m ) En pratique toute roue de moment cinétique 0.0032 Nms, peut être utilisée. Le choix est donc large.
Le module du moment magnétique, en régime de croisière, ne dépasse pas 0.002 A-m², donc très économique en énergie consommée.
Nul besoin de senseur solaire.
L'attitude de survie est très proche de celle de croisière, une seule rotation autour du tangage suffit pour passer de l'une à l'autre.
Le mode de survie peut être activé à tout moment et n'a pas besoin d'une position particulière sur orbite, pour être mis en oeuvre.
De plus, le retour au mode pointage nadir est très simple ( changement de consigne ), rapide, et surtout ne demande pas de modification de la vitesse de la roue, qui est et este donc utile à vitesse constante, dans tous les modes. Voir un essai de basculement d'un mode dans l'autre. En pratique, la loi de Laurens s'applique pour tous les modes, assurant, le détumbling, puis l'acquisition et le mode fin, puis éventuellement le mode survie, par simple changement de consigne.
Nul besoin de la mesure des vitesses angulaires. Seule une connaissance approximative de la position sur l'orbite est nécessaire, puisque c'est elle qui va permettre le calcul de la consigne.
Nul besoin de "désaturer" la roue. Elle est mise en rotation une seule fois, pour toute la mission.
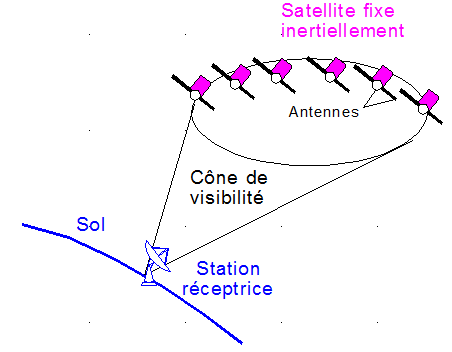
Sur le plan des télécommunications, il semble qu'avec des antennes longues qui dépassent largement la partie cylindrique du satellite, il ne devrait pas y avoir de souci. Une des deux antennes restera toujours horizontale, parallèle au sol. De plus l'antenne sera inertiellement fixe, l'autre d'ailleurs aussi. Une étude complémentaire est cependant nécessaire. Voir plus loin une amorce d'étude
En pratique, une seule loi de régulation permettra de réaliser tous les modes de fonctionnement ( "Détumbling", acquisition et mode fin de pointage nadir, mise en survie, retour de la survie vers le mode fin ) ( Voir les dernières simulations synthese.m est synthesT.m )
A Propos de la roue : les simulations ont parfaitement fonctionné avec une vitesse roue de -100 rd/s ( environ 15 tours/s ). Le moment d'inertie de la roue est J=3.2 e-5 m²-kg, celui du satellite autour de y est Iy =36 e-3. Disons que le rapport est de 100. Donc, un transfert de moment cinétique du satellite vers la roue va imposer au satellite de prendre 1 rd/s de vitesse angulaire. C'est beaucoup d'un seul coup, mais si pendant le détumbling, où les vitesses peuvent être de 15°/s ou 0.24 rd/s, il suffit de monter en vitesse par 100 impulsions de 0.01 rd/s ( 0.57 °/s ), sur 3000s pendant le détumbling. La roue va se mettre à son allure de croisière, sans que le satellite en soit affecté juste après l'injection. C'est la régulation qui amortit l'effet.
NB : Le problème sera résolu en lançant dès l'injection, la roue sous un couple de 1 e-6 Nm durant 2000 s ) Voir plus loin
3°) Optimisation approximative :
L'idée la plus simple pourrait consister pour rapprocher la normale panneau de la direction soleil, dans un premier temps, de faire "tandem" avec le soleil, donc de prendre b = -90°+d où d et la déclinaison solaire du jour J.
4°) Optimisation complète : Comment choisir le bon repère de consigne :
Simulation survfix1.m initialisée par beta_dat.m ( retrouver les fichiers ==>survfix1.zip )
Le cas de l'équinoxe de printemps est un cas d'école où sans calculs on aurait pu anticiper le résultat énergétique. Pour une application réelle on ne connaît pas d'avance le jour où des problèmes peuvent se poser. C'est ce jour là qu'il faudra choisir le bon angle b pour optimiser l'énergie. Nous convenons de mesurer positivement autour de Yc.
Ce problème peut être traité indépendamment de la simulation qui le validera. Il faut:
1 - Se donner le jour J, calculer l'unitaire soleil Us(J) dans XnYnZn, calculs aisés, réalisés plus haut
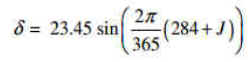 |
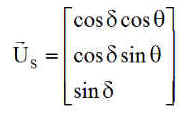 |
q
angle entre Xn et Us, fixé par l'heure H au nœud ascendant N, mesuré
autour de Zn
q = 90°+ 15°*( 12 - H ) = -142°.5, |
2 - Calculer Up(b) l'unitaire de la normale aux panneaux, dans XnYnZn
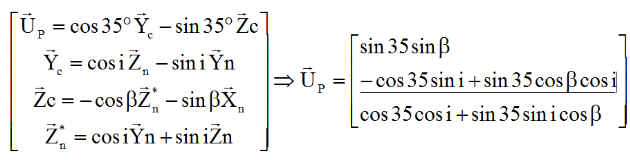
3 - Calculer la durée D de l'éclipse du jour J, sur la période T, opération effectuée par la fonction Teclipse.m par exemple Teclipse(181) = 1953 s
4 - Former la fonction
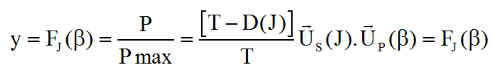
5 - Calculer la valeur de b donnant le maximum de la fonction, consigner ces résultats soigneusement et les mettre en mémoire à bord du satellite.
Pour ne pas "plomber" mes simulations, le calcul de l'angle optimal b qui est long, lorsque J = jour est donné, est exécuté directement dans le fichier d'initialisation qui ne fonctionne donc qu'une seule fois par simulation.
Exemple de résultat : pour le jour 181, au solstice d'été, la puissance recueillie pour une orientation b=303° ou Y=35° est de 11.03 Watts. Le premier graphe a été calculé avec le programme balayage.m. Le second reprends la valeur optimale de b calculée par ce programme et l'injecte dans la simulation qui valide la puissance moyenne de 11 Watts, pour le jour 181. On ne pouvait pas espérer mieux
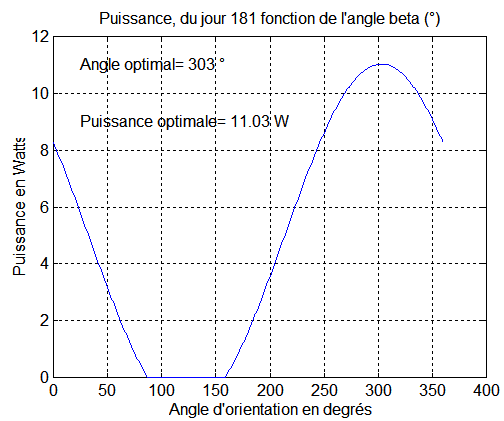
6 - Cette valeur déterminera le repère de consigne optimisé XcYcZc, pour le jour J de la mise en survie. La simulation donne
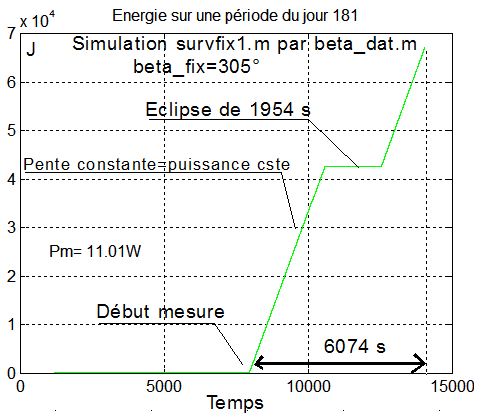
Confirmation indéniable par la simulation
5°) Optimisation complète ( suite ):
Il est intéressant de connaître la puissance espérée tout au long de l'année. Autant dire qu'il faut calculer la puissance maximale et l'angle d'orientation pour tous les jours de l'année. Le calcul fournit le graphe suivant donné par la fonction PbetaOpt.m initialisée par beta_dat.m ( La retrouver )
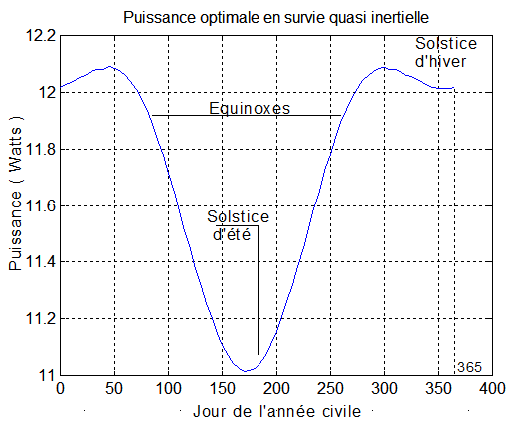
où l'on constate qu'on est capable de réaliser une survie avec au moins 11 Watts de puissance moyenne, ce qui est remarquable. La survie la plus défavorable est aux environs du solstice d'été.
Voyons maintenant, l'angle d'inclinaison à choisir : par exemple les jours 75 ou 275 ( au voisinage des équinoxes ), l'angle valant 270°, le satellite doit être couché parallèlement à la ligne des nœuds ou encore le plan ( x y ) parallèle au plan équatorial, avec l'axe Z+ vers le nœud ascendant.
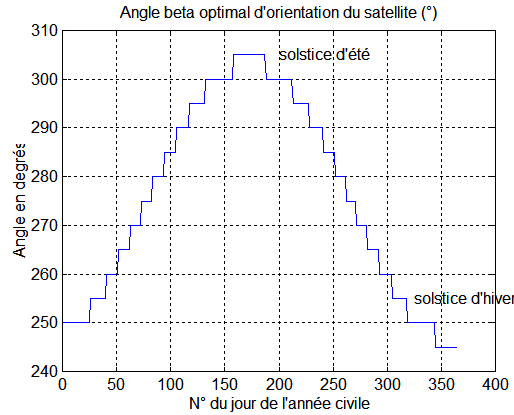
Ressources du calcul : Retrouver ces fichiers ==> surv_fix.zip
nanodat1.m : fichier d'initialisation et fourniture des données
eclipse.m : fonction y=eclipse(t) donne 1 ou 0 suivant qu'au temps t les panneaux sont éclirés ou pas
Beta_opt.m : fonction qui calcule la puissance pour un angle b donné, optimal ou pas
Teclipse.m : fonction qui retourne la durée de l'éclipse du jour choisi, l'initialisation par nanodat1 est nécessaire
balayage.m : programme de calcul ponctuel de l'angle beta_fix, optimal, et de la puissance optimale P_opt_fix pour un jour est donné. Une courbe de puissance est donnée fonction de l'angle b, pour confirmer l'extremum. Par exemple si jour=181 est donné dans nanodat1 balayage retourne beta optimal=303° et puissance moyenne optimale=11.03 W
BalayOpt.m : programme identique au précédent, sans courbe, mais transmettant beta_fix et P_opt_fix pour l'initialisation dans beta_dat.m
Pbetaopt : programme avec une boucle sur le jour, permettant le calcul de la puissance optimale et de l'angle beta_fix, pour tous les jours de l'année. Les résultats sont stockés dans un fichier Matlab --> PUIS_FIX.mat contenant les variables jour_beta de 1 à 365, la puissance optimale P_beta_opt et l'angle b optimal beta_optimal
6°) Expression calculée du quaternion d'attitude enfin de simulation:
Le calcul a été fait dans la page des résultats ( La voir ), la concordance des courbes des composantes du quaternion calculées et simulées est exceptionnellement précise ( voir les courbes ), ce qui valide le concept. Un calcul d'angles donne :
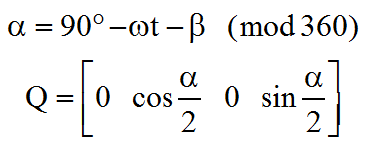
On découvre aussi qu'en fin de régulation l'axe de la rotation du quaternion est toujours la bissectrice intérieure de l'angle des vecteurs x et X. Pour le jour 181, b = 305°.
7°) Influence d'un retard introduit par le propagateur d'orbite:
C'est l'objet de survfix2.m où l'on peut choisir son retard DT qui décale le calcul du champ magnétique de DT. ( Retrouver les fichiers )
Par avance, on peut conclure qu'un retard du propagateur sur la position, n'aura pas grande influence sur la puissance vue la courbe donnant l'angle optimum ( position autour d'un extremum, bien plat )
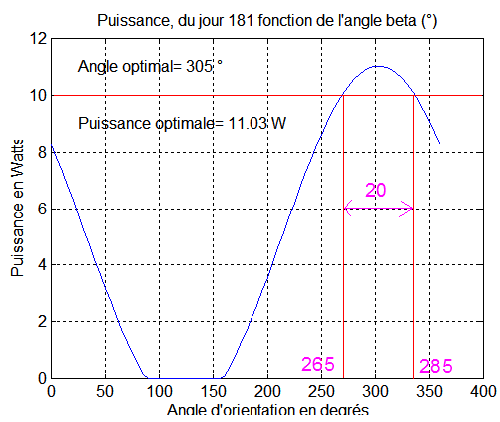
Pour descendre en dessous de 10 Watts, l'erreur sur l'angle b devrait dépasser 10° de part et d'autre de l'optimum 305°. Comme le champ magnétique est la boussole, qui grosso modo tourne de 180° sur une demi période de 6074 secondes, on peut apprécier le temps d'erreur de l'ordre de.
Dt = 3000/180*10 = 167 secondes
sur la trajectoire, l'écart en degrés est le même soit 10° environ. Voir les résultats concernant le décalage
8°) La mise en route de la roue:
Jusqu'à présent, la roue était supposée être à la vitesse angulaire qui donne un moment cinétique H = 0.0032 Nms. Pour celle que nous avons gardée, le moment d'inertie vaut JROUE = 3.2 e-5 m²kg, elle tourne donc à 100 rd/s ou 955 tours/mn.
Mais comment la mettre en régime de croisière? Pour ne pas déstabiliser le mode de travail en pointage fin nadir, il ne reste que la mise en rotation pendant le détumbling.
Solution : Dès l'injection du satellite, exercer un couple Cr constant, sur la roue durant un temps Dt, tel que:
1 - La roue atteigne son régime nominal à Wo =100 rd/s ( 955 tours/mn ), avant la fin du détumbling, vers 4000 s
2 - Que le couple ne dépasse pas le couple maximum admissible pour la roue, soit 4 e-6 Nm
3 - Que la vitesse angulaire du satellite en tangage ne soit pas supérieure aux vitesses extrêmes rencontrées en début d'injection, soit 15°/s
L'application exacte en (1) et approximative en (2) du théorème du moment cinétique à la roue et au satellite donne :
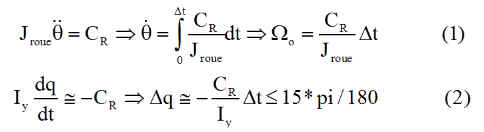
La relation (2) donne
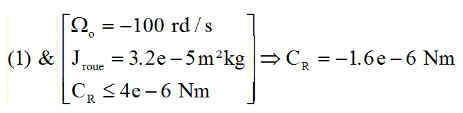
Résultat très largement compatible avec la relation (1) qui donne
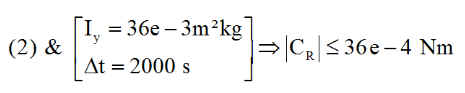
Ceci signifie que la mise en route de la roue au cours du détumbling est tout à fait transparente pour lui. Un couple constant, à 40% du couple maximum, appliqué pendant 2000 s conduira tranquillement la roue à sa vitesse de croisière qu'elle ne quittera plus jamais.
La vérification fait l'objet de synthesT.m ( Retrouver les fichiers ) où l'on constate que survie et mode fin ne sont pas du tout affectés par le lancement de la roue au cours de la phase de réduction des vitesses.(Voir les résultats ) La mise en route est visible sur le graphe qui suit:
|
Dt=2000 s |
************************************************ Fin provisoire **************************************************
8°) Que dire des télécommunications en mode survie?:
L'étude de l'angle b, en fonction du jour a fourni 245° < b < 305°, comme le montre le dessin suivant.
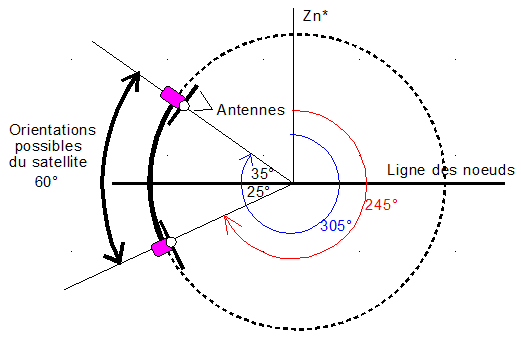
Il reste à traduire mathématiquement, comment on peut apprécier une communication correcte, suivant les coordonnées de la station sol et l'attitude du satellite et des antennes qui lui sont liées. Le problème est à priori, plutôt complexe.
X MISE EN MODE SURVIE QUASI INERTIELLE PAR LA ROUE PUIS RÉGULATION DE LAURENS :
Point de départ : le satellite est en mode normal fin, en pointage nadir, avec l'axe de tangage de sens contraire au moment cinétique orbital. Donc quasiment y=-Y et une vitesse de tangage opposé à la vitesse orbitale == > q = - wo = - 0.001 rd/s
Idée : Peut-être utiliser quelques tours de la roue pour passer du pointage nadir au pointage inertiel. En espérant un gain de temps et d'énergie!!!!
Pour l'instant hypothèse non testée. Plus tard si nécessaire!!!.
Je conserve quelques idées comme elles viennent :
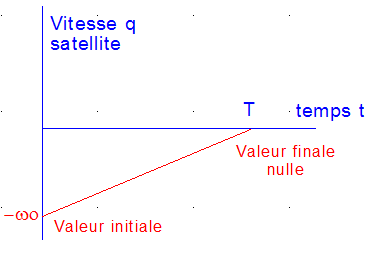
Imaginons que l'on veuille annuler la rotation satellite en pointage nadir pour le placer en pointage inertiel, tout en voulant le faire pivoter d'un angle Dq. Alors, si C est le couple, I le moment d'inertie, on a :
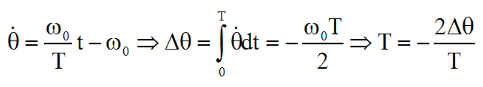
On peut déduire le couple roue nécessaire :
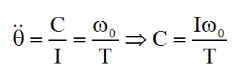
*****************************************************************************************************************
************************************ ANNEXES ******************************
1 - Vérifications de la fonction éclipse
a) H = 18 h et inclinaison 90°, delta=0° :
Pour cette orbite polaire et le soleil dans le plan normal à l'orbite et sur l'équateur, il n'y a pas d'éclipse et comme Y coïncide avec la direction du soleil, la normale décrit un cône qui fait toujours l'angle de 35° avec le soleil au rythme orbital. La puissance normale et la puissance "spinnée" doivent donc être toujours constantes et égale à Pmax*cos(35°) = 14.75 Watts, pour une énergie de 90000 joules/période ( OK )
b) H = 18 h et inclinaison 0°, delta=0° altitude nulle ( cas théorique ) :
Pour cette orbite équatoriale qui tourne d'Ouest en Est, le temps d'éclipse et celui d'éclairement sont égaux. La période tombe à 5069 secondes et effectivement les temps d'éclipse et d'éclairement sont égaux. D'abord éclipse puis éclairement.
Remarque : si l'inclinaison est prise 180°, alors les périodes sont inversées.
c) H = 18 h et inclinaison 180°, delta=0° :
Pour cette orbite équatoriale qui tourne d'Est en Ouest, après le nœud ascendant, le satellite est éclairé durant une demi période. La puissance est vérifiée au premier quart de la période. On observe que la non production d'énergie provient soit de l'éclipse soit d'une incidence négative hors éclipse.

d) H = 18 h et inclinaison 180°, delta=0° rayon_orbital = 2R :
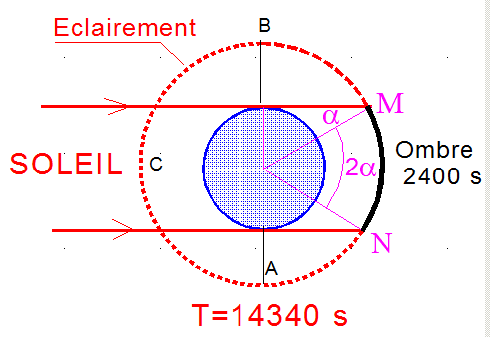
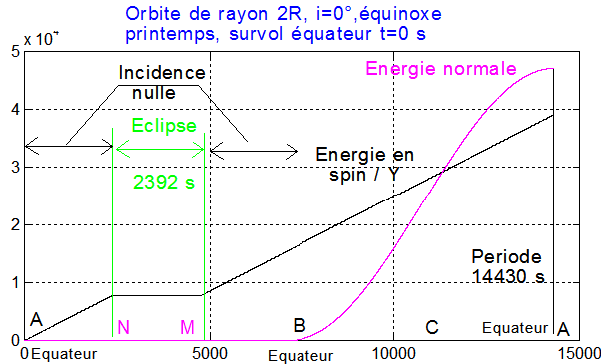
La période d'ombre est la partie MN sa durée est
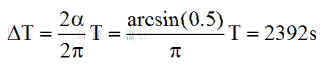
Ce que confirme une simulation Matlab de la fonction eclipse.m qui doit être initialisée par energdat.m
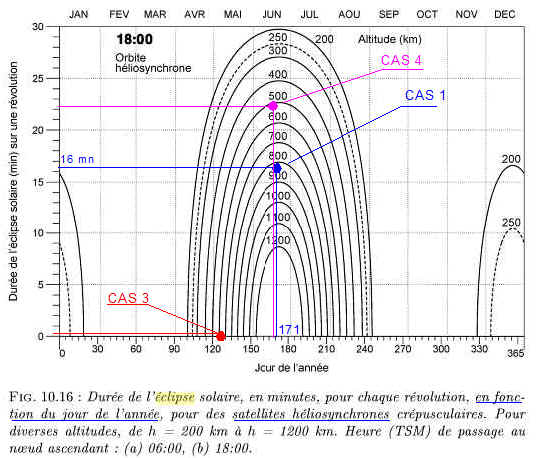
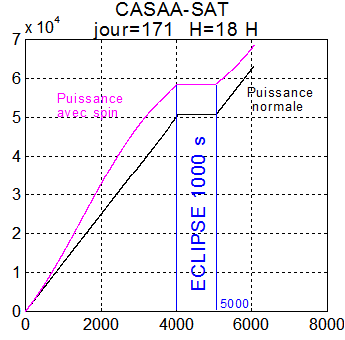
CAS 1 : Pour jour = 171 et 817 km et H=18h la simulation donne une éclipse de 1000 secondes environ, ce qui correspond à 16 mn du graphique. OK
Voir le point sur la figure plus haut
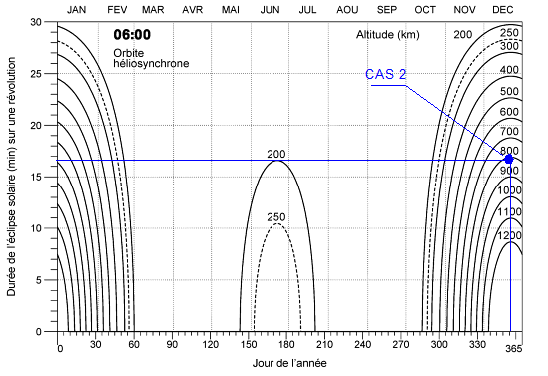
CAS 2 : Pour jour = 360 et 817 km et H = 6Hl, a simulation donne une éclipse de 1020 secondes environ, ce qui correspond à 17 mn du graphique.
Cependant aucune énergie n'est produite dans aucun des 2 modes "spinné" ou pas. La raison en est l'orientation des panneaux qui ne permet pas une incidence > 0. Vérification avec le point CAS 2 du graphique correspondant à H=6H ). OK
CAS 3 : Autour de J=125 et H=18 et 817 km l'éclipse est inexistante. L'énergie en mode normal varie entre 9 et 17.6 Watts. Le point remarquable qui a été analysé plus haut est la quasi égalité entre les énergies produites par les 2 modes. 81290 Watts en mode normal et 81320 Watts en mode survie spinné.
NB : Il pourrait être intéressant de montrer qu'en l'absence d'éclipse les énergies dans le mode normal et le mode "spinné" sont identiques. En présence d'éclipse l'énergie du mode normal est toujours plus grande que celle du mode "spinné".
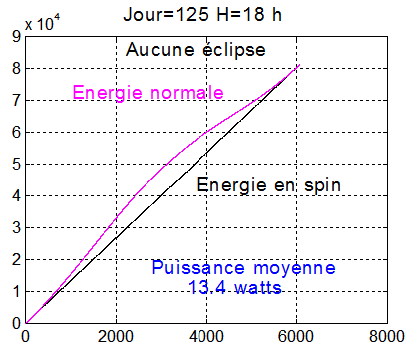
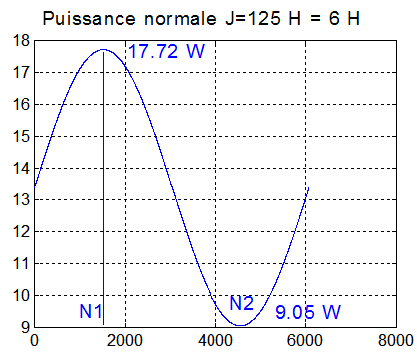
La courbe de la puissance normale est intéressante et permet de vérifier , à l'aide des 2 configurations extrêmes de la normale N aux panneaux
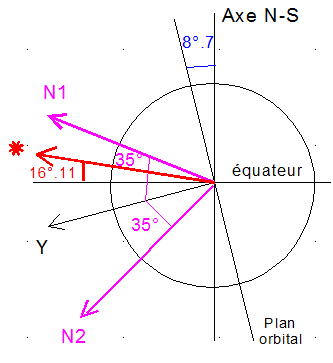 :
:
- Déclinaison = delta 23.45*cos(2*pi*(284+125)/365) = 16°.11
- Pmin =18 * cos(35°+16°.11+8°.7) = 9.05 Watts avec la normale N2
-Pmax= 18 * cos(35°-16°.11-8°.7) = 17.72 Watts avec la normale N1
CAS 4 : Pour jour=170, H=18 H altitude 500 km et inclinaison adaptée 97°.5, le calcul donne environ 1450 secondes correspondant à 24 mn environ, ce qui est indiqué sur le diagramme vu plus haut.
CONCLUSION : les tests semblent prouver l'exactitude de la fonction eclipse.m et des simulations qui l'utilisent!!!
2 - Vérifications des calculs de l'unitaire soleil en axes satellite
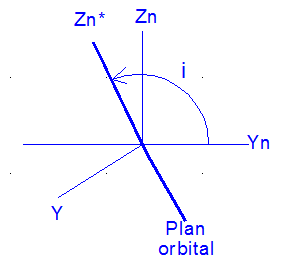
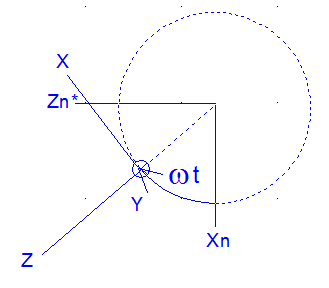
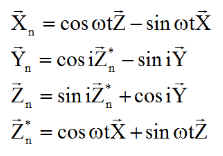
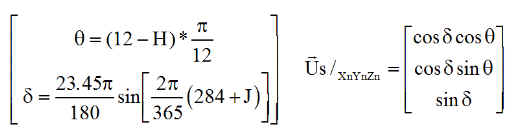
La matrice de changement de base de XYZ à XnYnZn est
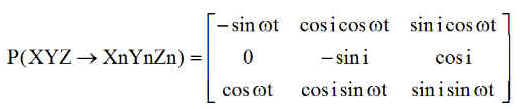
4 - Vérifications de la fonction puissanc.m
On prend le cas simple où le soleil se trouve exactement dans l'axe de l'orbite héliocentrique. Donc le soleil est sur l'axe Y
Le calcul donne le jour J=58.9201 ==> delta=23.45*sin(2*pi/365(284+103.08)) = -8°.7
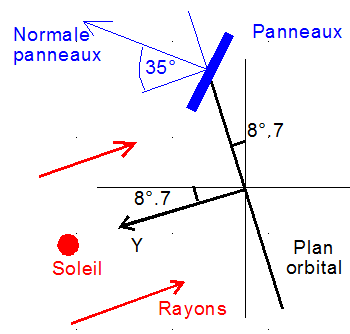
Figure au temps t=T/4 =6074/4=1518.75 s
Dans ces conditions, la puissance est constante tout au long de l'orbite et vaut P=18*cos(35°)=14.745 W et l'énergie produite sur une orbite E=6074*P=89560 J
Us=[0 -0.9885 -0.1513] Np=[0 -0.8965 0.4431] ou encore [0 - cos(35-8.7) sin(35-8.7)]
La fonction puissanc.m donne puissanc(58.9201)=14.7447 W On retrouve donc le bon résultat
La simulation energies.m donne bien une puissance constante de 14.745 W et une énergie produite de 90000 Joules
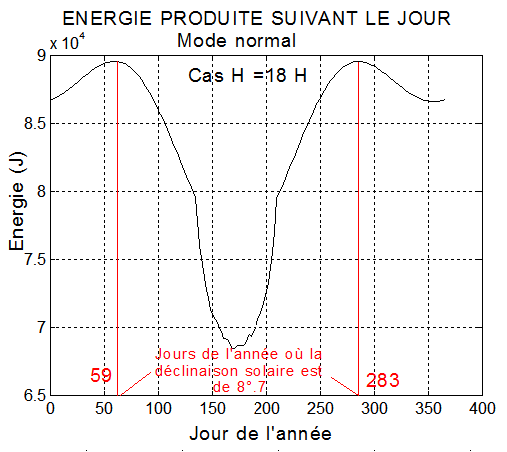
L'exécution du programme enerJour.m permet de donner l'énergie produite tout au long de l'année, ci-dessous pour H=18H et 817 km d'altitude.
************ FIN ***********
Robert Guiziou Janvier-février 2016