![]()
MISE EN SPIN D'UN SATELLITE PAR
MAGNÉTOCOUPLEURS SANS ROUE DE RÉACTION
![]()
![]()
Les notions présentées dans cette page, ont pour origine, un dépôt de brevet européen référencé ainsi que ses auteurs par :
Date de publication et mention de la délivrance du brevet EP1312997B1
08.03.2006 Bulletin 2006/10
Date de publication de la demande:
21.05.2003 Bulletin 2003/21? (73) Titulaire: EADS ASTRIUM SAS? 31402 Toulouse Cedex 4 (FR)
Inventeurs: • Defendini, Ange, 31070 Toulouse Cedex (FR) et • Lagadec, Kristen, 31070 Toulouse Cedex (FR)
Ma seule contribution consistera en une mise en forme, que j'espère aussi synthétique que possible, pour une utilisation pédagogique. Dans ce site dédié à l'espace, et une rubrique spécialement consacrée au SCAO de nanosatellites, simple et à bas coût, l'utilisation des magnétocoupleurs y trouve toute sa place.
BREVET EUROPEEN EP 1 312 997 B1
I CONDITIONS DE MISE EN OEUVRE DE L'INVENTION :
Elle consiste en la commande d'un SCA de satellite en orbite basse, utilisant exclusivement le champ magnétique terrestre, sans autre actuateur.
La vitesse angulaire orbitale est notée wo.
1°) Rappels :
On trouvera sur ce site 2 types de commande basées sur une mesure du champ magnétique B, toutes deux ayant fait l'objet d'un dépôt de brevet.
1 - La régulation en Bpoint ( dérivée de B ) de M DAMILANO. Procédé qui réduit les vitesses angulaires aléatoires après l'injection, mais qui ne conduit pas à une stabilisation complète. Le satellite garde une rotation angulaire égale à 2 fois la vitesse angulaire orbitale.
2 - La régulation boussole avec un champ magnétique de consigne et une roue de réaction, de M LAURENS.
2°) But à atteindre :
Réaliser un couple de mise en rotation du satellite à une vitesse angulaire w > 2 wo autour d’un axe de spin choisi par l'utilisateur, axe à priori quelconque du satellite.
3°)Moyens embarqués :
Un magnétomètre 3 axes fournissant, en axes satellite :
1 - Une mesure des composantes du champ magnétique local B, notée Bm
2 - Une mesure calculée de la variation de B en fonction du temps, donc des composantes de la dérivée de B
Trois magnétocoupleurs pour générer le couple de commande C, par interaction avec le champ magnétique local.
Une électronique de calcul du moment magnétique M à créer pour obtenir le couple de commande à l'aide de courants dont l'intensité est calculée pour chaque bobine réalisant une des composantes de M.
![]()
II MOMENT MAGNÉTIQUE A CALCULER ET ASPECT ÉNERGÉTIQUE :
1°) Rappel :
Le procédé dérive de celui de M Damilano, qui utilise la loi Bpoint ( pour dire "dérivée de B" ) par le moment magnétique ci-dessous
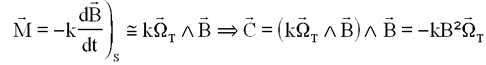
qui donne un couple de commande amortissant la rotation transversale WT.
2°) Adaptation du procédé :
Il est fait le choix d'un axe de spin u lié au satellite et d'une vitesse angulaire w.
![]()
Les auteurs imaginent une " attitude de consigne", qui est l'attitude souhaitée en fin de régulation ( ou en régulation permanente ). C'est celle d'un satellite "spinné" autour d'un axe de spin u choisi en fonction de la mission ou d'une opération particulière, avec une vitesse de spin w également choisie :
- suffisamment grande pour générer un moment cinétique capable d'amener, par effet d'alignement gyroscopique, l'axe de spin normal au plan orbital.
- mais pas trop grande pour éviter une raideur gyroscopique gênante et les réactions de nutation.
Ainsi, dans cette configuration, la vitesse de l'extrémité de B, vue du satellite, en attitude idéale de rotation est choisie comme " vitesse de consigne ", en effet en repère absolu B apparaît presque fixe, comparé à son évolution vue du satellite, donc :
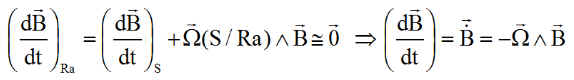
Donc pour une rotation quelconque W et avec une excellente approximation, vue du satellite la dérivée de B vaut sensiblement :
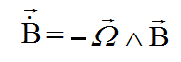
Elle est donc un excellent indicateur de la rotation transversale au champ magnétique.
a) Vitesse de consigne :
Dans le brevet, j'ai interprété sa définition comme étant la vitesse idéale que devrait avoir l'extrémité de B, vue du satellite, s'il était en spin parfait autour de u à la vitesse w:
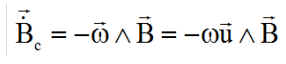
b) Moment magnétique :
C'est une adaptation ou un compromis entre la méthode en Bpoint de M Damilano et celle, avec une consigne sur B, de M Laurens, le moment magnétique est proportionnel à l'écart entre la consigne et la valeur actuelle, avec un gain K>0 à choisir en fonction des inerties et de la stabilité à obtenir ( pas si simple !!!) :
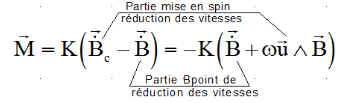 |
Pour le meilleur choix du gain K consulter la page dédiée et la prise en compte des inerties.
c) Moment de commande généré :
C'est classiquement, pour un magnétocoupleur :
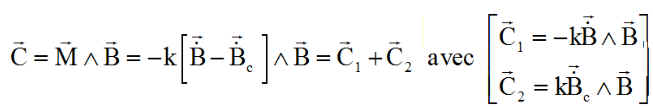
Le calcul explicité de C2 fournit explicitement:
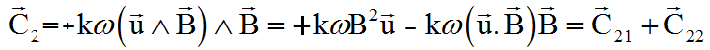
Le couple C1 est typiquement celui de la régulation Bpoint dont on montre ( voir l'aspect énergétique ) qu'il participe à la réduction des vitesses
La partie C21 est un couple de mise en rotation du satellite autour de l'axe choisi u, c'est la MISE EN SPIN autour de l'axe u à vitesse w.
La partie C22 apparaît comme un couple parasite de mise en rotation autour de l'axe du champ B, fort heureusement variable et qui donc sera plus ou moins amorti par le couple C1 en mode Bpoint qui dégrade l'énergie de rotation due à la rotation transverse au champ magnétique.
NB1 : Il est à prévoir que ce deuxième couple génèrera de la nutation par couplage avec le spin.
NB2 : La partie C22 contenant le produit scalaire u.B aura tendance à disparaître si l'axe u s'aligne sur la normale au plan orbital, du moins pour les orbites quasi polaires, ce qui est le cas des orbites héliosynchrones.
d) Aspect énergétique :
Calculons la puissance du couple C. Pour la partie C1 type Bpoint, le calcul a déjà été fait et donne, en fonction de la rotation transverse au champ magnétique B:
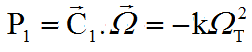
NB : on ne peut pas en déduire que l'énergie cinétique tend vers 0, car si le satellite est calé sur le vecteur B, il reste la rotation axiale autour de B, qui n'est pas traitée.
Le bilan général de la régulation montre une puissance négative, assurant dans tous les cas une réduction de la vitesse angulaire transversale au champ magnétique terrestre, comme dans le mode Bpoint de M Damilano. Il reste donc à montrer que cette nouvelle régulation apporte un plus, et plus précisément une convergence de l'attitude vers une stabilisation, précisée par les auteurs avec l'axe u normal au plan orbital, avec un spin de vitesse angulaire w. Ce spin aurait donc un effet stabilisant par effet d'alignement gyroscopique, avec un seul alignement stable celui où la vitesse angulaire de spin est parallèle à celle de la rotation orbitale.
d) Considération particulière :
Il est indéniable que les vitesses angulaires du satellite sont réduites, grâce à la partie Bpoint. Cependant, si la dérivée de B est nulle en axes satellite, cela montre que le satellite se cale sur le champ magnétique, avec un mouvement de tangage à une pulsation double de la pulsation orbitale donc à 2 wo . Cette vitesse angulaire très faible n'offre pas assez de raideur gyroscopique pour garantir la stabilité.
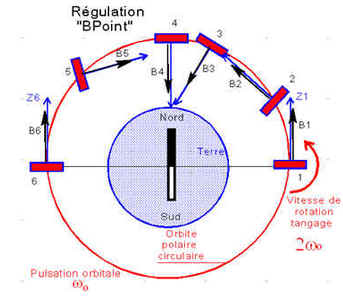
e) Conclusions :
Nous savons que la régulation en Bpoint fonctionne infailliblement, dans toutes les conditions, pour réduire les vitesses angulaires résultant du transfert de moment cinétique entre le lanceur et la charge utile, au moment de l'impulsion qui largue le satellite, mais sans stabiliser complètement le satellite qui se cale sur les lignes de champ magnétiques. On peut encore dire que ce dernier "voit" B comme quasiment fixe. Avec la remarque de d) le satellite est animé en moyenne d'une vitesse angulaire 2wo autour de Y.
Si donc le satellite acquiert une rotation de spin wU, la vitesse de B vue du satellite ne peut être due qu'à ce spin. Quand le satellite aura rejoint sa position définitive, avec le spin pratiquement normal au plan orbital, sa vitesse angulaire orbitale sera soit 2wo + w soit 2wo - w. La propriété d'alignement des axes de rotation va donc privilégier la première valeur pour un état stable, sans danger de retournement.
La mise en spin s’effectue en parallèle dès la fin de réduction des vitesses. La vitesse angulaire atteinte correspond à la somme w + 2wo de la vitesse de consigne de rotation en axes satellite et de la rotation des lignes de champ magnétique le long de l’orbite.
III LOIS ET SIMULATIONS PRÉCONISÉES ET ESSAYÉES :
1°) MISE EN SPIN A VITESSE ET AXE CHOISIS :
SIMULATION DE BASE ( regspin0.m Initialisation par spin0dat.m ) : Récupérable regspin0.zip
NB : Pour que la mise en spin conduise à un spin > 0 autour de l'axe y, il faut un couple C21 > 0 sur y, donc w > 0 et U= y.
a) Loi adoptée :
La plus simple consiste à commencer la régulation dès le lancement, avec la loi ci dessous. Les simulations montrent que même en mouvement très turbulent, après l'injection, la mise en spin fonctionne correctement et s'obtient en moins de 3 orbites. Cependant, l'alignement sur l'axe orbital de tangage n'est pas aussi parfait que l'indique le brevet. Mes simulations peuvent laisser un "mésalignement" maximum de 20°. Peut-être n'ai-je pas toutes les subtilités en main??
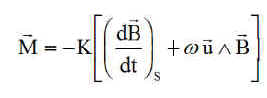
b) Variante à la régulation :
SIMULATION DE BASE ( regspin0.m Initialisation par spin0dat.m ) : Récupérable regspin0.zip
Pour éviter d'exercer le couple de mise en spin alors que le satellite est toujours turbulent après l'injection, j'essaye de procéder en 2 temps:
1 - Ne connaissant pas les vitesses au départ, je traite d'abord la réduction des vitesses en module, jusqu'à un seuil plancher de 2*w.
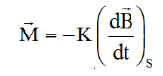
2 - Ensuite au franchissement en décroissance de ce seuil, j'autorise la régulation complète de mise en spin avec:
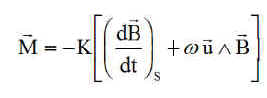
NB : rien n'oblige à utiliser le même gain K pour les 2 lois. Cette simulation peut être testée avec 3 niveaux de vitesses initiales turbulentes ( normales, moyennes et fortes )
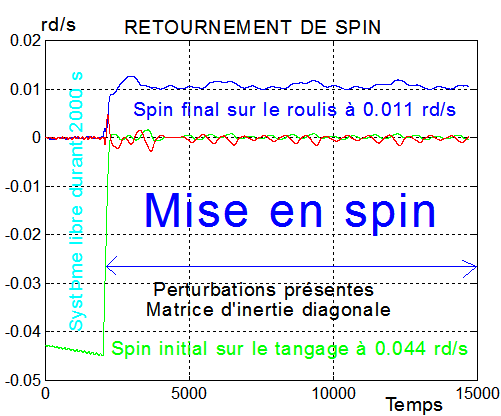
RÉSULTATS : pour w = 0.00875 rd/s K=600000 SI
Le brevet prévoit une mise en spin à W = w +2*w0 soit 0.0875 + 0.002 = 0.01075 rd/s, pratiquement 0.011 rd/s. La simulation donne une moyenne de 0.011 rd/s. Le brevet précise que que la mise en spin est durable H = Iy * q = 36e-3*0.011 mNs = 0.000396 mNs, la simulation donne une moyenne à 0.0004 mNs ( Résultats excellents )
Matrice d'inertie diagonale Ir=32e-3;It=36e-3;Il=22e-3;Irt=0;Irl=0;Itl=0;
|
Vitesses angulaires: on constate la réduction du lacet et du roulis et une mise en spin tangage q à vitesse angulaire 0.01 rd/s soit effectivement W = w +2*w0 |
L'axe y se rapproche en moyenne de 15° de la normale Y au plan orbital, le satellite est ainsi stabilisé, en spin quasiment normal au plan orbital |
|
Le moment cinétique se stabilise |
L'énergie de rotation décroît durant le mode Bpoint et se stabilise avec le spin autour de y à une valeur 1.8 e-7 Joules due au spin en grande partie.
|
Ci-dessous un cas d'école d'un satellite de révolution sans perturbations
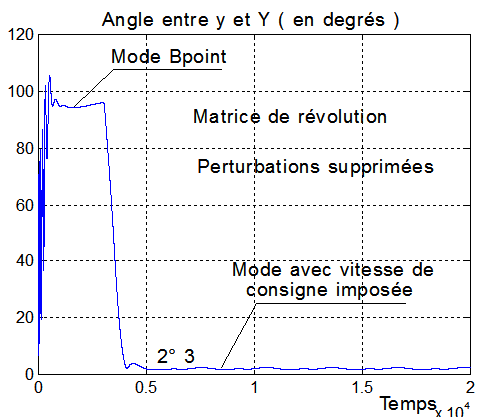
NB : Avec une matrice d'inertie non diagonale et les perturbations, la convergence vers un spin normal au plan orbital est moins nette
2°) EXEMPLE DE RETOURNEMENT DE -Y à +Y :
SIMULATION DE BASE ( regspin1.m Initialisation par spin1dat.m ) : Récupérable regspin1.zip
Voir aussi une version modifiée regspinx.m initialisée par spinxdat.m Récupérable regspin1.zip
Le satellite est supposé initialement avec une rotation pratiquement sur l'axe tangage ( w = - 0.05 rd/s axe_spin = [0 1 0] ), avec des angles pratiquement nuls. Donc xyz presque confondus avec XYZ, mais avec une rotation de - 0.05 rd/s
| % Initialisation en vitesses (rd/s) v_roulis0=0.001; v_tangage0=-0.05; v_lacet0=0.002; % Initialisation en position (rd) roulis0=0.02; tangage0=-0.01; lacet0=0.03; |
Loi
avec w = 0.00875 rd/s K=300000 SI axe_spin = [0 1 0] |
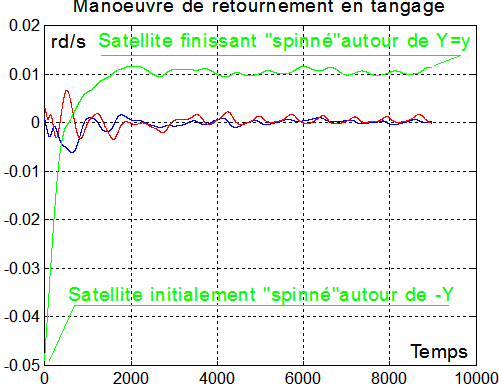
Le retournement "spinné" se produit en 2000 secondes.
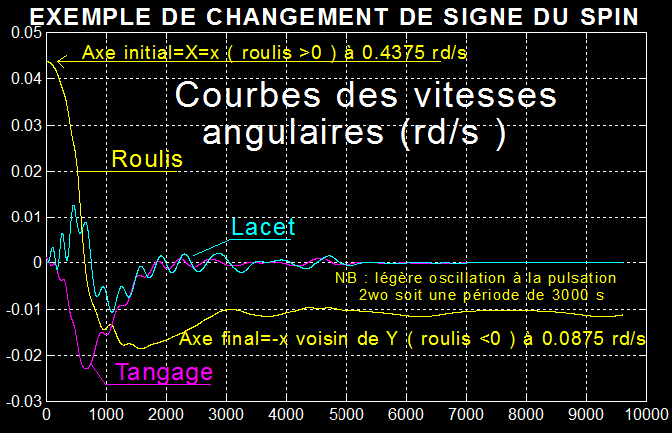
Exemple de retournement avec changement de vitesse
de spin et changement de direction de spin
Ci-dessous la même manœuvre de changement de spin ( signe et niveau ) autour de l'axe roulis x, en 3000 secondes, les perturbations ont été annulées. On observera la fameuse oscillation parasite à la pulsation double de la pulsation orbitale, soit 2wo avec une période de 3000 s moitié de celle du satellite ( 6000 secondes ).
Attention à ne pas confondre ceci avec un retournement de l'axe en repère orbital. Les axes de spin restent liés au satellite, mais si au départ le spin est sur X, à l'arrivée ce ne sera pas le cas, par contre l'axe final vient se caler sur la normale au plan orbital.
3°) MODE SURVIE :
Normalement, dans toute mission spatiale, un mode de fonctionnement dit " MODE SURVIE " est prévu pour permettre la gestion d'un incident important demandant du temps de réflexion et des reconfigurations éventuelles des systèmes de commande ou de la mission elle-même.
Ce mode est activé en présence d'un problème grave. Le but est de mettre assez rapidement le satellite dans un configuration stable, connue dite de sécurité, permettant un contact radio avec le sol et une alimentation suffisante en énergie pour gérer les ressources vitales.
Limitons nous aux orbites héliosynchrones, donc quasiment polaires. La position du soleil vue de l'orbite dépend de l'heure au nœud ascendant:
12 h ou 24 h : alors la direction du soleil, en période d'éclairement est proche du plan orbital. Dans ce cas là, si les panneaux sont dans un plan P, et si A ou B sont 2 axes orthogonaux dans P, la mise en "spin" autour de A ou B assurera un éclairement partiel des panneaux solaires. Ce mode est dit "MODE BARBECUE" car le système ressemble à une rôtissoire ( satellite ) avec le soleil la source de chaleur ( mieux lumière ).
6 h ou 18 h : alors la direction du soleil, en période d'éclairement est proche de l'axe tangage du plan orbital. Dans ce cas là, si les panneaux sont dans un plan P, et si A est un axe orthogonal à P, la mise en "spin" autour de A assurera un éclairement satisfaisant des panneaux solaires, hors éclipse. Ce mode est dit "MODE MOULIN A VENT" car le système ressemble à une moulin ( le satellite ) avec le soleil ( la source de vent , mieux la lumière ).
Le mode survie demandant une certaine stabilité devra donc utiliser une mise en spin. L'idéal serait un spin vers le soleil, autour d'une direction parallèle à la normale aux panneaux. Les simulations suivantes vont permettre les choix.
a) Exemple de mise en spin autour d'un axe fixe par rapport au satellite ou encore xyz
Ci-dessous le lacet, apparemment très stable ( axe_spin=[0 0 1] )
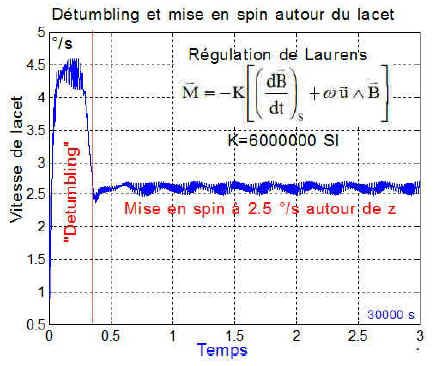
de même que le spin autour du tangage ( axe_spin=[0 1 0] )
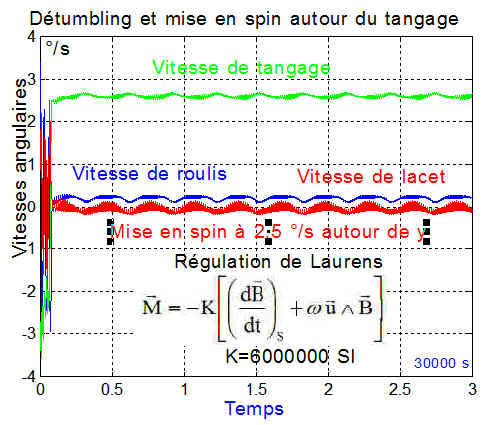
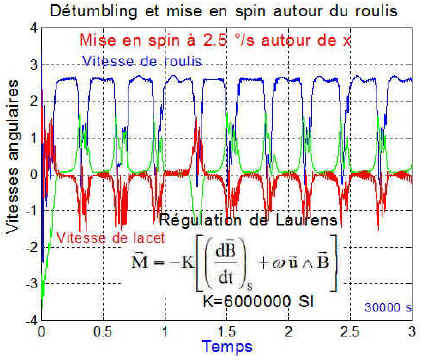
Le spin en roulis tente de s'établir mais est visiblement périodiquement instable ( axe_spin=[1 0 0] ), entraînant par couplage une instabilité sur tous les axes
Pour finir, voici la mise en spin autour d'une direction parallèle à l'axe des panneaux ==> axe_spin=[0 -cos(35*pi/180) -sin(35*pi/180)];
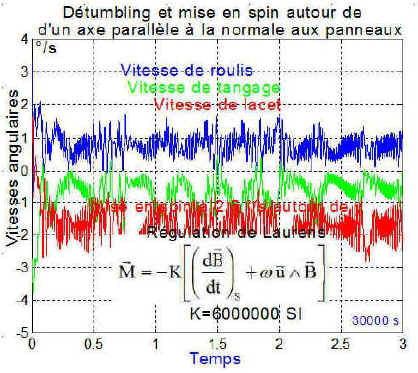
Les vitesses angulaires sont chaotiques
Le tracé de la vitesse angulaire de spin autour de la normale, donne avec la projection adéquate sur l'axe de spin choisi ==> plot(temps,(p*axe_spin(1)+q*axe_spin(2)+r*axe_spin(3))*180/pi)
Nous sommes loin d'un état stable!!!
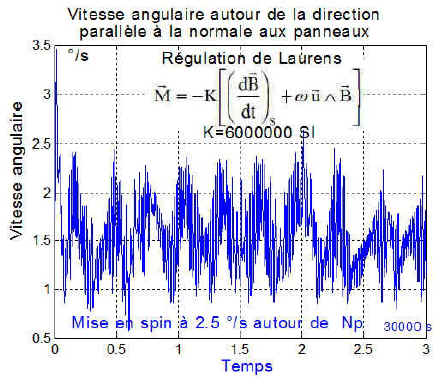
b) Conclusion : en cause probablement la position moyenne des inerties autour de x et de la parallèle à la normale.
Cette nouvelle simulation totalement indépendante de celle de Steyn, semble confirmer l'impossibilité de "spinner" le satellite autour d'un axe parallèle à la normale aux panneaux. Sauf, bien sûr à revoir la géométrie du satellite!!!
******************************** Fin de page, septembre 2015 **********************************