|
PHASE DE RÉDUCTION DES VITESSES ACQUISITION D'ATTITUDE ( DÉTUMBLING ) UTILISATION D'UNE LOI "Bpoint" SANS ROUE |
![]()
|
|
I Technologies disponible dans le nanosatellite II Théorie |
Rédigé janvier 2014, revu juin 2014
![]()
Lors de la mise en orbite, c'est la phase cruciale, juste après l'injection en orbite, phase où les vitesses angulaires peuvent être très importantes et l'attitude aléatoirement éloignée de l'attitude de travail. En anglais on dit que c'est la période de "Tumbling".
Cette phase d'acquisition se décompose en 2 :
1 - Phase de réduction des vitesses angulaires "Detumbling": Avec l'utilisation du champ magnétique B, on sait que le contrôle autour de B est impossible, donc les angles ne sont pas contrôlés et le hasard pourrait très bien conduire à un satellite à l'envers de son attitude de travail ou en position quelconque.
2 - Phase de pointage ou d'acquisition d'attitude de travail. Quelquefois la phase 2 est traitée en même temps que la phase 1
Cette phase est critique, car les panneaux solaires ne sont pas encore pleinement fonctionnels, les communications avec le sol quasi impossibles. Le satellite doit donc se gérer en automatique, avec une dépense minimale d'énergie. Cette configuration n'est pas loin du mode survie mis en oeuvre lors d'incidents sérieux de fonctionnement pour des satellites plus importants.
I LES TECHNOLOGIES DISPONIBLES POUR UN NANOSATELLITE :
Sans faire le tour de toutes les technologies possibles, indiquons que notre satellite est muni , outre l'électronique et l'informatique ) de capteurs et d'actuateurs suivants, en attendant le choix définitif:
- Capteurs de position et d'attitude
- Capteurs de vitesses angulaires
- Magnétomètres restituant
Le champ magnétique en axes satellite, éventuellement complété par un champ magnétique embarqué très précis ( par exemple IGRF )
La dérivée de ce champ magnétique, vue par le satellite, soit si S est le satellite (ou repère qui lui est lié ) et B le champ magnétique de composantes ( Bx, By, Bz ) dans S
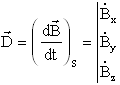
- Trois magnétocoupleurs, pouvant interagir avec le champ magnétique pour générer un couple sur le satellite
- Une roue de réaction disposée sur l'axe de tangage, pouvant générer un couple sur l' axe tangage ( non utilisée pour cette phase initiale ).
- Pourquoi pas un senseur solaire venant à l'appui d'un magnétomètre 3 axes pour permettre la restitution d'attitude.
NB 1 : le choix se fera sur une technologie minimale permettant la mission à moindre coût.
NB 2 : dans la suite, nos simulations utiliseront un champ magnétique approché et simplifié, analytique largement suffisant pour valider la méthode.
Gardons à l'esprit, que l'essentiel dans la première phase, est de dissiper l'énergie de rotation, pour réduire les vitesses angulaires. La logique indique que tout amortissement s'exerce sur les vitesses, donc on s'intéresse aux dérivées des angles ( vitesse de rotation ) et du champ magnétique terrestre.
Ro est le repère inertiel et S = ( x y z ) un repère lié au satellite S. Entre les deux, le repère orbital est R ( X Y Z ).
La génération de couples par des magnétocoupleurs, se heurte à l'impossibilité de générer un couple suivant l'axe du champ B. On peut en déduire que le champ B ne sera pas utile pour réduire d'une manière ou d'une autre une composante de rotation dans le sens de B.
NB : Fort heureusement le champ magnétique varie en direction tout au long de l'orbite, ce qui minimise cette servitude.
Seule la composante transversale de la rotation peut donc faire l'objet d'un traitement.
Ainsi on est amené à décomposer la rotation absolue du satellite en 2 termes, un transverse à B l'autre sur l'axe de B
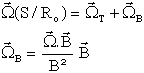
La dérivée de B se calcule classiquement par :
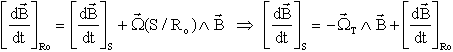
Dans la dérivée satellite du champ, il apparaît 2 termes, le premier qui ne dépend que du mouvement de rotation du satellite, le deuxième uniquement du mouvement orbital.
Faisons une figure, suffisamment explicite:
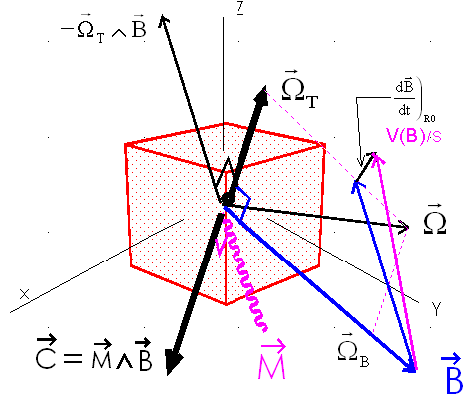
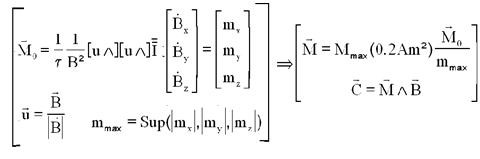
Pour "contrer" la rotation transversale en utilisant une bobine programmée de moment magnétique M, donnant un couple opposé à la rotation transversale, et efficace, on peut choisir M comme suit
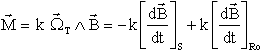
D'où le choix, connaissant la dérivée satellite de B, de prendre pour M le premier terme et considérer le second comme perturbateur ( espéré faible il sera sensiblement évalué plus loin ). k est un gain scalaire.
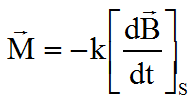
En résumé, on admet que la part essentielle de la dérivée de B ( vue du satellite ) provient des vitesses angulaires du satellite. Ainsi, le couple magnétique généré, s'oppose, en partie, à la rotation transversale, comme le montre le calcul simple qui suit,.
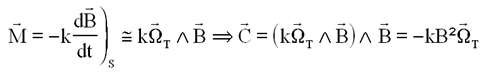
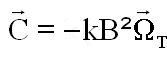
d'où de toute évidence l'effet amortisseur efficace à coup sûr.
REMARQUE TRÈS IMPORTANTE :
Le fait d'avoir négligé la dérivée absolue de B dans Ro est strictement équivalent à dire que, vues du repère absolu, les variations dues aux coordonnées géographiques de B sont petites devant celles dues à la rotation satellite, du moins dans la première phase de détumbling, qu'on peut considérer B fixe dans le repère absolu. Nous reprendrons plus loin cette idée.
Cependant cette hypothèse impose de cesser la régulation lorsque la dérivée satellite est, en norme inférieure à 1/5 de la norme de la vitesse absolue de B.
Une simulation rapide (Enregistrer et exécuter derivb00.m) donne les composantes de la dérivée absolue.
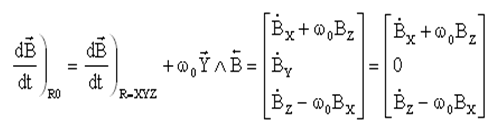
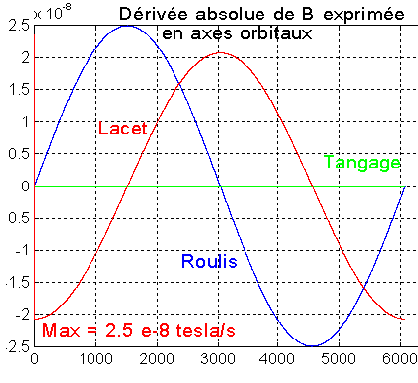
Donc avec un maximum de 2.5 e-8 tesla/s. Comme la dérivée conservée est au maximum WT Bmax, avec Bmax de l'ordre de 5 e-5, pour que l'approximation reste valide il faut que le terme négligé soit au moins 4 ou 5 fois plus petit que celui conservé ce qui donne
![]()
effectivement en dessous de cette valeur, le satellite sera mis en contrôle fin.
Le calcul de la puissance de ce couple est simple
![]()
Remarque : On pourrait dès lors s'inquiéter de ce que la composante de la rotation portée par B n'est pas réduite. C'est vrai, sauf que la grande variabilité du champ magnétique le long d'une orbite presque polaire est grande. L'effet amortisseur agira donc ailleurs sur cette composante qui n'apparaîtra pas toujours colinéaire à B, en d'autres points de l'orbite.
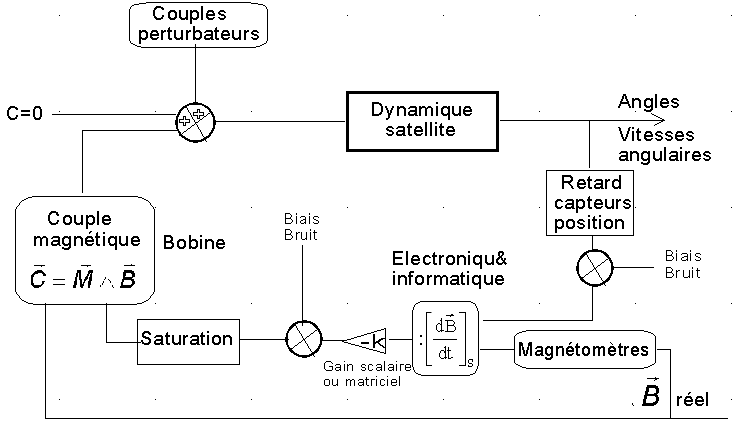
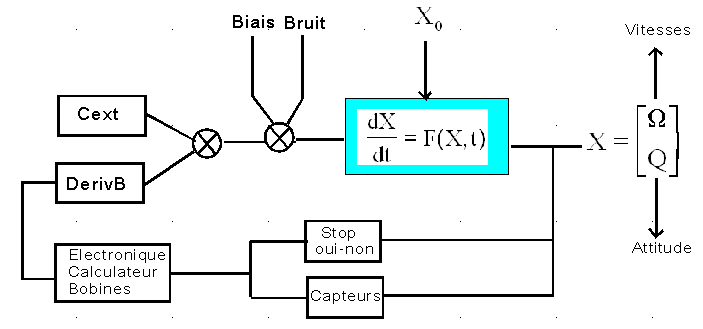
Le schéma bloc du SCA d'acquisition pourrait sensiblement se résumer à ceci ( je ne suis pas un spécialiste des chaînes fonctionnelles )
3°) Étude mathématiques plus fine et exacte de cette régulation :
Je reprends quelques idées déjà présentées dans mon site en 1994 qui m'avaient été suggérées par M Damilano ( brevet déposé par lui ).
Partant de
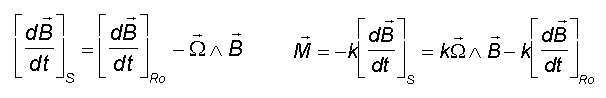
on obtient
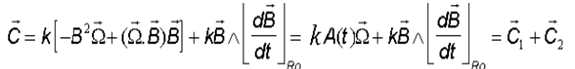
Le couple contient deux termes de natures très différentes, le premier C1 qui dépend linéairement du vecteur W fait apparaître une matrice A(t) de cette relation linéaire, dépendant du temps (sur une orbite circulaire le champ ne dépend que de l'angle de rotation j(t) = wo t pour nous t = 0 est un passage équateur ) et le deuxième terme C2 ne dépend que du temps et donc de la position sur l'orbite. Il pourrait d'ailleurs s'évaluer analytiquement avec une bonne précision..
a) Couple C1 et matrice A(t) :
Le lecteur se convaincra que dans la base du satellite on a : C1 = A(t) W
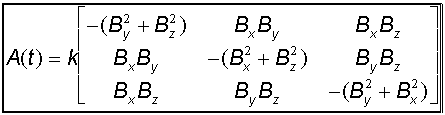
Le polynôme caractéristique de A(t) est :
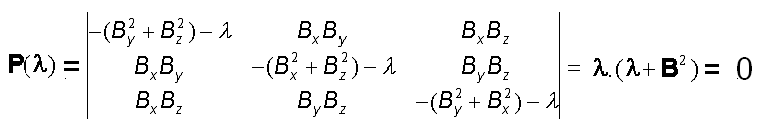
Cette matrice symétrique, possède une valeur propre l = 0 associée à un vecteur propre colinéaire à B et une valeur propre double négative. l = - B² associée au sous espace propre de dimension 2 orthogonal à B? Ce qui confirme des remarques déjà faites sur l'impossibilité de contrôler une rotation parallèle à B et l'effet amortisseur ( grâce au signe moins ) sur la composante transversale de la rotation.
2° ) Réflexions sur le couple C2
Ce couple ne dépend que du temps et varie de manière périodique.
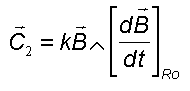
Vérification par une simulation Matlab : derivb00.m, en utilisant la dérivation intermédiaire dans le repère orbital R
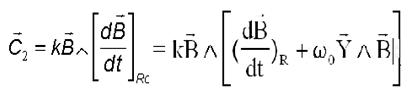
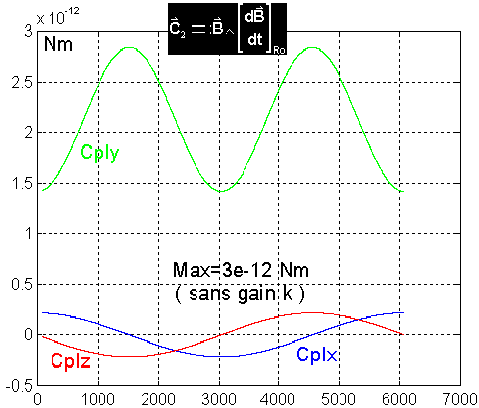
La simulation fournit un maximum de 3 e-12 Nm sur l'axe Y normal au plan orbital et un couple d'environ 3 e-13 Nm sur les axes X et Z du repère orbital. Ces valeurs sont très faibles devant celles des perturbations.
Conséquences : il apparaîtra comme un couple perturbateur jouant le même rôle que le couple aérodynamique sur l'axe de tangage. Son effet serait donc un dépointage statique par rapport à la géocentrique, en l'absence de régulation. Sur les autres axes l'influence est anecdotique.
III AMÉLIORATION DE LA RÉGULATION :
La première fois que j'ai abordé l'utilisation de la dérivée de B, j'ai eu, dans les années 1990,un contact fructueux avec un ingénieur M DAMILANO, de chez MATRA( à l'époque ), spécialiste du SCAO. La chance a voulu qu'à l'occasion de recherches sur Internet, je le retrouve comme inventeur de nombreux brevets concernant notamment l'acquisition d'attitude par l'utilisation de la loi qu'il nomme en ' Loi en Bpoint'.
Je donne donc en annexe et en le citant une petite partie de ses idées et remarques, qui me semblent vraiment utiles à notre projet
Voir ANNEXES Il me faisait remarquer que le gain scalaire k choisi pour amplifier la dérivée de B, ne tenait pas du tout compte des inerties du satellite. Or mécaniquement, l'inertie, comme son nom l'indique, va peser plus ou moins sur la rapidité de la réponse et donc chaque axe a sa constante de temps. Certains axes seront plus difficiles à contrôler que d'autres. C'est souvent le lacet qui est difficile à maîtriser, d'autant plus qu'il n'y a pas de gradient de gravité sur cet axe pour des satellites de révolution inertielle autour de z.
Je traduis donc ses conseils très précis par les considérations qui suivent,
1° ) Notations
|
|
2° ) Prise en compte des inerties
Le principe de base consiste toujours à utiliser la dérivée du champ magnétique terrestre, mais en adoptant un gain K matriciel prenant en compte les inerties satellite. Le moment magnétique est toujours choisi comme précédemment, mais avec une matrice de gains K dont l'expression s'imposera en temps voulu.
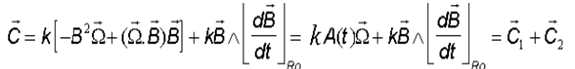
Posons A(t) = B².P où P est la matrice
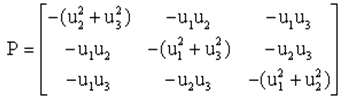
Plus haut, nous avons montré que A(t) est diagonalisable dans un repère X Y u où E = ( X Y ) est l'espace vectoriel orthogonal à u . Les valeurs propres de P sont -1, -1, 0, donc P(t) s'écrit très simplement dans cette base
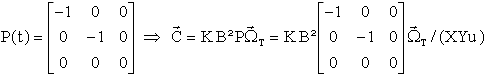
Rappel : Le fait d'avoir supposé que la dérivée absolue de B, ne dépendait que de la rotation de S, revient pratiquement à considérer le vecteur B comme quasi fixe dans le repère absolu.
Continuant sur cette idée, un repère R* = X Y u associé à B peut donc être considéré comme quasiment fixe et pris comme un repère absolu Ra, le TMC donne dans ce repère.
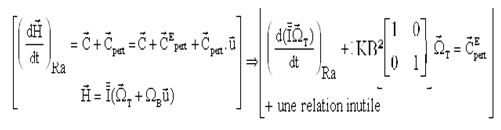
Nous limitant au plan E orthogonal à u, il vient
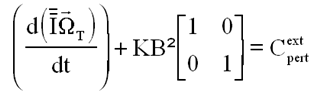
Venons en donc à l'idée du spécialiste de MATRA qui explique, pouvoir faire en sorte, que toutes les composantes de la rotation transversale soient régulées avec la même constante de temps. C'est à dire avec une équation de la forme générale (1) ci-dessous, ce qui amène à avoir pour WT une équation du type (2), montrant que les composantes transversales sont traitées à hauteur de l'inertie qui les concerne ( en clair éviter un petit couple sur une grosse inertie )
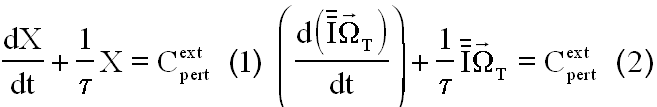
Ce qui est réalisable avec la matrice K ci-dessous( ce que le lecteur vérifiera ):
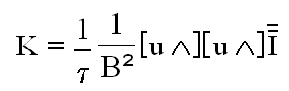
fournissant un moment magnétique M par la relation matricielle:
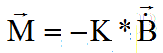
3° ) Vérification
Avec l'expression de K, le couple C s'écrit , compte tenu de la relation
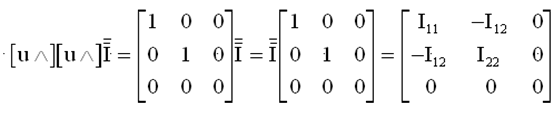
donnant
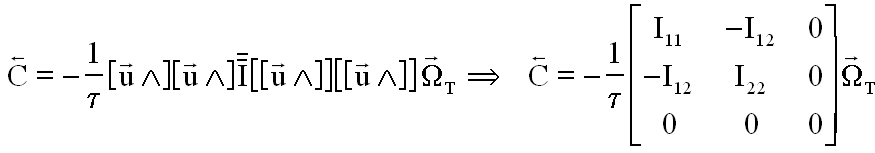
montrant que le couple C s'oppose à la rotation transversale et que les inerties sont prises en compte dans le gain sur chaque axe ( forte inertie sur un axe entraîne un couple en proportion de cette inertie sur l'axe).
On constatera aussi que la puissance dissipée (sous l'hypothèse du seul mouvement autour du centre d'inertie) est
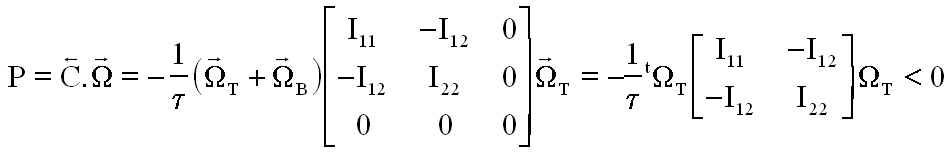
3° ) ESTIMATIONS LIÉES A LA COMMANDE
Le moment magnétique maximum M d'une bobine est de 0.2 Am2, on travaillera donc à 50% de cette valeur, soit 0.1 Am².
Le champ magnétique moyen B est de l'ordre de 2 à 4 e-5 Teslas. Choisissons la moyenne 3 e-5 teslas
Donc le couple moyen peut être au maximum M*B de l'ordre de 3 e-6 Nm, ce qui permet de largement dépasser le niveau des couples perturbateurs.
En adoptant pour I le moment d'inertie maximum du satellite, soit celui en tangage de 36 e-3 kgm², il apparaît que la vitesse angulaire transversale w et la constante de temps t, satisfont sensiblement )à la relation
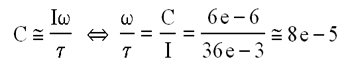
Autant dire et c'est très logique, plus les vitesses angulaires sont grandes, plus la constante de temps est grande et l'opération de réduction des vitesses longue.
NB : Se pose donc la question de la faisabilité? A-t-on assez de temps et d'énergie, après l'injection, pour réduire totalement les vitesses absolues?
En ce qui me concerne, je choisis une constante de temps de 1 h, ce qui devrait conduire à un bon amortissement en 3 à 5 heures( 20000 s environ ). La vitesse angulaire maximale supportée est donc de l'ordre de 0.3 rd/s. C'est déjà beaucoup
IV LA SIMULATION DU "DETUMBLING" :
Nous sommes plutôt dans le vague car :
- Ne possédant pas d'estimation des valeurs maximales des vitesse angulaires
- Les angles pouvant être quelconques, les angles d'Euler ou de Cardan risquent de poser des problèmes de singularités
Donc, il va falloir s'adresser aux quaternions, ce qui, au départ n'est pas une mince affaire
- L'énergie disponible n'est pas encore bien connue
- Ni le temps maximal de l'opération
- Au final, si le nanosatellite est à l'envers, quelle sera la procédure pour le retourner?
Nous commençons par l'aspect mathématique, qui une fois au point nous permettra de réfléchir avec plus de sérénité.
A - LES PARAMÈTRES ET LES ÉQUATIONS:
Dans le cas d'un mouvement inconnu, c'est le cas après l'injection, l'utilisation d'un paramétrage angulaire ( Angles Cardan ou d'Euler ) peut conduire à des singularités et des "divisions par 0" ce que les calculateurs n'aiment pas.
Une solution, pour l'attitude est de représenter l'attitude par un quaternion, qui lui est défini en toute circonstance. Les vitesses seront données par le vecteur rotation.
On introduit donc un vecteur d'état à 7 composantes, comprenant la rotation inertielle W et le quaternion d'attitude Q du satellite par rapport au repère orbital relatif X Y Z
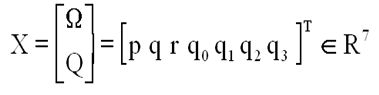
Vous trouverez ( adresse ), les équations matricielles de comportement du quaternion Q ( pour ce cas particulier où Q représente l'attitude relative dans le repère orbital R = XYZ) et de W avec le TMC.
wo est la vitesse orbitale
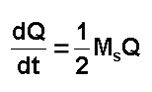
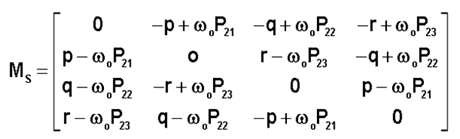
Le second membre devra contenir tous les couples en jeu, y compris celui de la commande avec la dérivée de B.
Les équations utilisent 2 matrices, Ms et la matrice d'inertie I
B - LE SYSTÈME DIFFÉRENTIEL SOUS FORME CANONIQUE:
Le TMC donne avec des notations évidentes
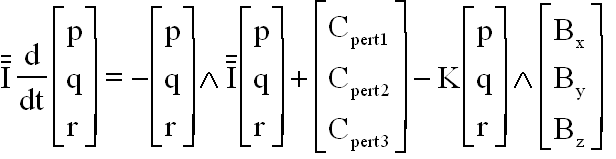
Ainsi le vecteur d'état X vérifie une équation de forme classique pour l'intégration:
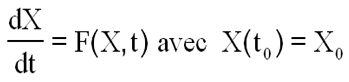
F comporte 7 lignes, les 3 premières déduites du TMC et les 4 dernières du comportement de Q
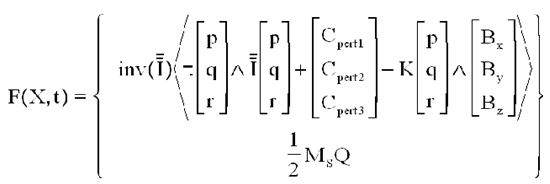
Le schéma bloc de la simulation pourrait ressembler à :
La récupération des angles pourrait s'opérer par les relations suivantes où la difficulté d'une division par 0 est maîtrisée par arctang2:
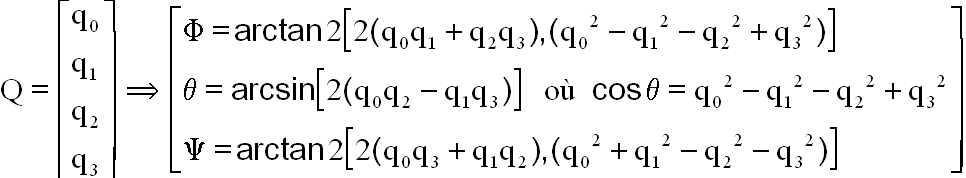
Obtention de ces relations en utilisant la matrice de passage exprimée avec les angles et celle exprimée avec le quaternion.
REMARQUE ESSENTIELLE :
Quand l'amortissement sera mis en place, il ne faudra pas oublier que ce sont les composantes de la rotation absolue qui sont réduites voire annulées. Ce qui signifie que notre nanosatellite sera fixe ou quasi fixe en repère inertiel. Il sera pointé inertiel. Il restera donc une rotation de tangage à annuler, si on veut respecter la consigne d'alignement sur le repère orbital XYZ.
Or l'application de ce satellite nécessite qu'il soit pointé Terre, ce qui demandera de le faire tourner autour du tangage pour aligner ses axes sur ceux du repère orbital. C'est donc une phase à anticiper et résoudre!!
D - LES VÉRIFICATIONS POSSIBLES AVANT INTRODUCTION DES COUPLES EXTERNES:
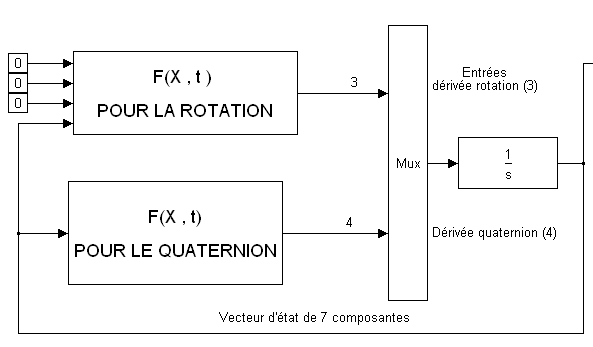
S'agissant d'un seul solide, dans le champ de gravitation, si on oublie le gradient de gravité, on est devant un problème classique dit de Poinsot :
VERIFICATION DES EQUATIONS DU TMC : Ces équations sont indépendantes de celles du quaternion, donc peuvent se vérifier directement en ne regardant que les composantes p q r.
1 - Avec une matrice d'inertie quelconque et sans couples externes, gradient éliminé, l'énergie doit se conserver OK Simulation réussie
2 - Avec une matrice d'inertie de révolution autour de z, donc avec D = Irl = 0, et des vitesses angulaires nulles, on doit retrouver le pointage inertiel parfait, qui doit se traduire par un quaternion Q constant en repère inertiel et donc avec une composante sur Y constante et des composantes sinusoïdales sur X et Y, à la période orbitale. OK Simulation réussie
3 - Avec une matrice d'inertie de révolution autour de z, donc avec D =0, une rotation axiale ( lacet ro ) et une rotation transversale ( par exemple de roulis w ), on doit retrouver les résultats classiques du mouvement de Poinsot, à savoir:
- Le moment cinétique est constant de 2 manières Vérification réussie
- En module et alors A²p²+B²q+c²r²=H² = cste & p²+q²+r² = cste et dans le repère inertiel, il faut alors imposer à H un changement d'axes faisant passer du repère XYZ à un repère inertiel, celui de XYZ au passage équateur. OK simulation réussie
- Un mouvement de l'axe z, conique avec un cône centré sur une direction inertielle fixe, une ouverture a du cône donnée par
tg(a)=I22 w / I33 ro
VÉRIFICATION DES ÉQUATIONS DU QUATERNION :
Le second module, intègre le quaternion, avec la connaissance de p q r. On peut vérifier qu'il fonctionne correctement, en essayant de retrouver la ROTATION SATELLITE PAR RAPPORT AU REPERE ORBITAL grâce à la relation ( voir cours 1 ou cours 2), exprimée en repère satellite.
![]()
étant entendu que la multiplication est celle de l'espace des quaternions. Je crée une fonction produit de 2 quaternions p et q, nommée prodquat(p,q). Rappelons le mode de calcul utilisant l'écriture avec partie réelle et partie vectorielle
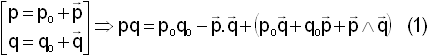
Quelques remarques ou résultats:
1 - La normalisation du quaternion fonctionne parfaitement bien, avec un écart entre le max de la norme et le min de l'ordre de 4 10-15
2 - Le calcul du vecteur rotation absolue du satellite par les quaternions et par le TMC donne le même résultat
3 - Le calcul de l'énergie donne un résultat identique par toutes les méthodes
CONCLUSION -> INTEGRATEUR AU POINT
4 -On passe à la mise en place des perturbations:
a) Le gradient de gravité seul, qui devrait conduire à une oscillation stable en roulis et tangage, avec un lacet divergent, car le gradient ne joue pas sur le lacet.
NB :Pour une plus grande efficacité du gradient, je redescends le satellite à 300 km du sol
5 - On peut tester l'amortissement sur le cas simple suivant:
- Matrice inertie cylindrique
- Seul mouvement de lacet
- Orbite strictement polaire
- Champ magnétique dipolaire n'ayant donc que 2 composantes BX et BY dans le plan orbital
Le moment créé, en prenant un gain à une dimension, est alors strictement porté par l'axe de tangage, sans termes parasites.
5 - On peut aussi avec le seul gradient de gravité en jeu, tester avec une matrice d'inertie toujours diagonale, mais avec axes diversifiés, les oscillations stables en roulis tangage, avec un lacet qui s'échappe.
E - LES PERTURBATIONS:
Commençons par la plus connue, celle due au gradient de gravité.
1- Gradient de gravité : voir page dédiée
Puisque Z est la géocentrique pointée zénith, l'expression bien connue est donnée par:
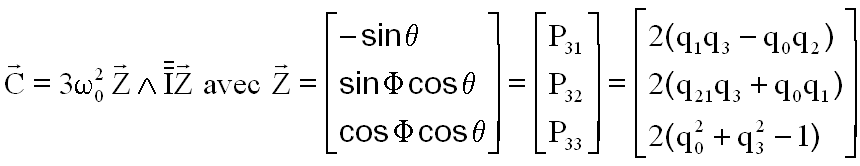
On reconnaît la matrice d'inertie I, les éléments de la matrice de passage de R = XYZ à S = xyz et la pulsation orbitale wo. La programmation ne posera pas de problème, avec le vecteur d'état qui contient le quaternion d'attitude Q
Avec les 3 inerties principales distinctes, dans le bon ordre, un semblant de stabilisation devrait apparaître sur les 3 axes, seul le produit d'inertie I23 pourrait réserver une surprise.
NB : Cependant dans la réduction des vitesses angulaires, le gradient sera simplement anecdotique.
2 - AUTRES PERTURBATIONS:
Identiques à celles du pointage fin.
F : LA REGULATION PAR LA DERIVEE DU CHAMP MAGNETIQUE:
NB : Dans les conditions réelles, la dérivée du champ est fournie par le boîtier des magnétomètres, en parallèle avec le champ magnétique B, connu à bord, dans les axes satellite.
MON CHOIX: J'ai un champ B analytique, connu en axes orbitaux XYZ. Je le transforme en axes satellite xyz et je l'utilise tel quel ainsi que sa dérivée, calculée avec l'opérateur Matlab. En pratique la dérivée est fournie par l'électronique.
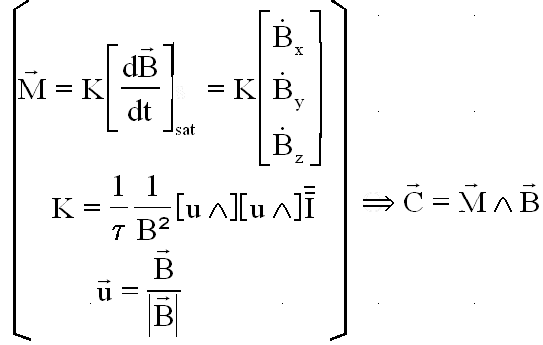
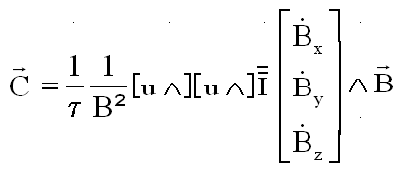
Voir plus loin, la commande optimale permettant de réduire au maximum le temps de "DETUMBLING" tout en travaillant à la limite des possibilité des magnétocoupleurs.
NOTE PARTICULIÈRE DE PROGRAMMATION :
Le cahier des charges impose un moment magnétique maximum pour les bobines, de valeur 0.2 Am². Il est strictement impossible de prévoir ce que seront les valeurs des moments magnétiques programmés. Donc, il faut limiter ces moments magnétiques. Deux moyens se présentent
1- Des blocs limiteurs d'amplitude en saturation?
Cette méthode a l'inconvénient de ne pas maintenir le moment magnétique en proportion, le couple ensuite calculé, ne sera pas opposé à la rotation transversale. Je m'explique si la rotation est [4 6 -8] que le moment est M=[-0.04 -0.06 +0.08], on le garde ( il est proportionnel à la rotation) mais s'il vaut [0.2 -0.3 +0.4] on le tronque à [0.2 -0.2 +0.2] et il n'est plus proportionnel à la rotation, son effet pourrait être délétère.
2- Limiter le niveau des moments magnétiques directement dans la fonction qui les génère. Le calcul ci-dessous préservera la proportionnalité tout en limitant la valeur à 0.2 Am²
mt_mgn=K_mat*B_prime';
% Moment magnétique
calculé
maxi=[abs(mt_mgn(1)),abs(mt_mgn(2)),abs(mt_mgn(3))];
% Test du maximum
test=max(maxi);
if
test>=0.2
y=0.2*mt_mgn/test;
% Moment limité proportionnellement
end
if
test<0.2
y=mt_mgn; % Moment conservé proportionnellement
end
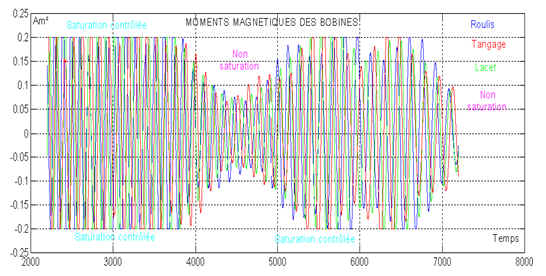
3- Commande optimale : Solution adoptée :
a) Limiter à chaque instant le niveau de la bobine la plus sollicitée, tout en gardant la proportionnalité.
b) En fin de régulation, la vitesse angulaire transversale diminue et donc les bobines ne sont plus utilisées à leur potentiel maximum. Or cette phase de réduction des vitesses doit être la plus rapide possible. Donc il faut relever le moment magnétique de celle qui est le plus sollicitée à 0.2 Am², tout en gardant la proportionnalité. On aura ainsi minimisé la durée de la phase de réduction. ce qui m'a conduit à cette programmation que l'on retrouvera dans la fonction saturmom.m, récupérable en format txt
if
test>=0.2
y=0.2*mt_mgn/test;
end
if
test<0.2
y=mt_mgn;
y=0.2*mt_mgn/test;
end
CONCLUSION SUR LA COMMANDE OPTIMALE
( Si nécessaire pour écourter l'acquisition, mais prudence !! ):
NB : Dans ces conditions, le choix d'un gain t n'est plus vraiment nécessaire. En somme le gain évolue en continu pour optimiser le temps de réduction des vitesses.
G : LES SIMULATIONS : Récupérer les fichiers de simulation
NB : Je profite de mes travaux en 1994, où j'avais déjà programmé un amortissement avec la dérivée de B.
Quelques résultats avec la programmation optimale, (satellite de révolution, orbite normale )
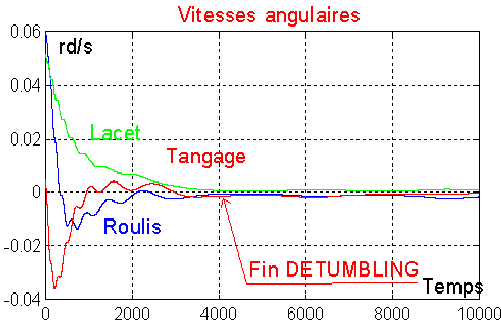
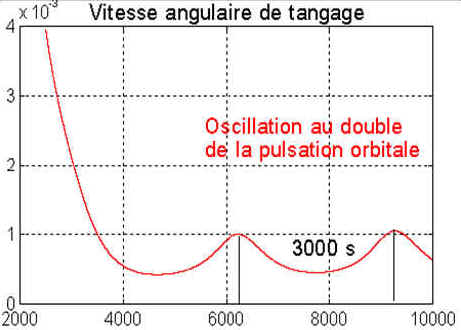
La rotation tangage tend vers une oscillation à une période moitié
de la période orbitale, soit environ 3000 secondes
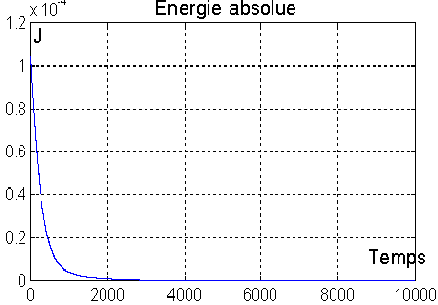
L'énergie est bien dissipée en continu. Le detumbling est terminé en
une heure environ.
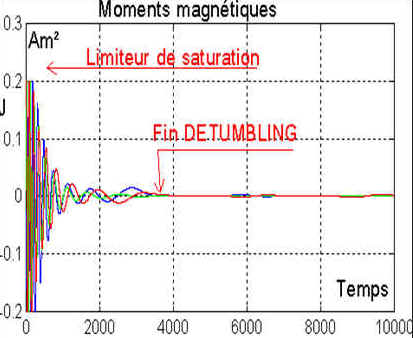
|
ENSEIGNEMENT A TIRER : Bien que la simulation soit convaincante, en ce qui concerne la dissipation d'énergie, qui ne fait aucun doute, elle ne suffira pas à obtenir l'acquisition d'une attitude correcte, car les angles ne sont pas ramenés près de 0. Récupérer les fichiers de simulation simulation ( regderb.m ) Comme le préconise M DAMILANO, il faut utiliser la roue pour "forcer" au moins le tangage à stabiliser son axe perpendiculairement au plan orbital. |
*************************************************************************
Guiziou Robert janvier 2013, revu juin 2014, revu février 2016
http://tel.archives-ouvertes.fr/docs/00/58/55/25/PDF/NGUYEN_Hoang_Van_2011_archivage.pdf
http://michel.llibre.pagesperso-orange.fr/docs/quaternions.pdf
LES IDEES DE M DAMILANO:
NB : Les parties rouges retiennent particulièrement mon attention
Récupérées à http://www.google.com/patents/EP0778201B1?cl=fr
Description
[0001]
La présente invention concerne les procédés de contrôle de l'attitude d'un satellite placé sur une orbite suffisamment basse pour que l'intensité du champ magnétique terrestre autorise une mesure d'attitude à l'aide d'un magnétomètre à trois axes et une commande de modification d'attitude par interaction de magnéto coupleurs portés par le satellite avec le champ magnétique terrestre.
[0002]
Pratiquement cette condition est remplie lorsque le satellite est, sur au moins une partie de son orbite, à une altitude inférieure à 2000 kilomètres.
[0003]
On connaît déjà un procédé de commande d'attitude permettant de réduire les vitesses de rotation du satellite lorsqu'il est largué par son lanceur et d'orienter un axe lié au satellite normalement au plan de l'orbite. Suivant ce procédé, utilisant une loi dite "en B point" pour indiquer qu'elle fait intervenir la dérivée du champ magnétique terrestre B, on mesure le champ magnétique terrestre suivant les trois axes d'un repère de référence liée au satellite, on dérive les mesures par rapport au temps, on multiplie les dérivées par un gain et on fait passer un courant représentatif du résultat dans des magnéto-coupleurs pour créer des moments magnétiques qui tendent à garder le satellite fixe par rapport aux lignes de force du champ magnétique terrestre.
[0004]
Ce procédé est simple. Il n'utilise que des capteurs fiables et peu coûteux et les actionneurs qui sont normalement employés sur tout satellite en orbite basse, c'est-à-dire des magnéto-coupleurs, en plus des roues ou volants d'inertie prévus dans tous les cas pour créer un moment cinétique interne au satellite. Il évite l'utilisation de tuyères de propulsion qui consomment des ergols et perturbent l'orbite ou de gyroscopes qui sont peu fiables. Il dissipe de l'énergie proportionnellement à la vitesse de rotation du satellite, de sorte que la convergence est assurée dans tous les cas et que le satellite se stabilise.
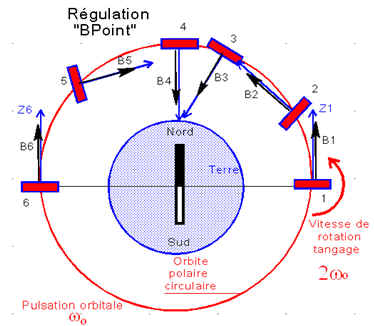
Les lignes de force du champ magnétique de la terre T ont, dans un plan passant par les pôles, l'allure générale montrée en figure 1. Un satellite placé sur une orbite polaire basse 10 croise ces lignes de force suivant un angle important, sauf à proximité de l'équateur, ce qui permet, connaissant la configuration du champ magnétique et la position du satellite sur son orbite, de calculer son attitude à partir des mesures fournies par un magnétomètre trois axes et de créer des couples de rotation à l'aide de magnéto-coupleurs. Au surplus, l'utilisation de la loi en B point permet de dissiper l'énergie de rotation que présente le satellite après séparation du lanceur, ou en cas d'incident, jusqu'à ce que le satellite soit fixe par rapport aux lignes de force du champ magnétique terrestre, ce qui provoque une rotation du satellite, à deux fois la pulsation orbitale ω0, autour de la normale au plan de l'orbite.
Explications personnelles: Dans une régulation idéale en "BPoint", la dérivée du champ magnétique en axes satellite est nulle si le champ garde une direction constante dans le satellite. Le croquis montre bien, par exemple que si Z reste aligné avec ce champ , c'est le cas du croquis, alors quand le satellite parcourt une demi-orbite, il effectue un tour complet autour de l'axe de tangage.
Conclusion: La régulation en BPoint conduit, si elle se prolonge, à un tangage établi à 2 fois la pulsation orbitale.
[0005]
En contrepartie, la loi en B point provoque finalement la rotation du satellite à une vitesse égale à deux fois la pulsation orbitale (c'est-à-dire à raison de deux tours sur lui-même par orbite) autour d'un axe normal au plan de l'orbite, c'est-à-dire autour de l'axe de tangage
.Pour différentes missions, cette rotation a des inconvénients. En particulier, elle réduit considérablement l'ensoleillement moyen de générateurs solaires portés par le satellite, lorsque ces générateurs ne sont pas orientables, sur des orbites ayant une faible inclinaison i sur l'équateur ou sur des orbites d'inclinaison moyenne lorsque le nœud ascendant est proche de 12 heures ou 24 heures en heure locale.
[0006]
La présente invention vise à fournir un procédé permettant de réduire les inconvénients essentiels de la loi B point, en effectuant une acquisition solaire sans pour autant exiger la mise en oeuvre de gyroscopes et/ou de tuyères.
[0007]
Dans ce but, l'invention propose un procédé suivant la revendication 1.
[0008]
Bien que la commande en tangage puisse être réalisée à l'aide des magnéto-coupleurs, il est plus avantageux de le faire en modifiant la vitesse des volants d'inertie autour d'une valeur de consigne, et annulant alors les commandes des magnéto-coupleurs dont l'axe est suivant les directions de roulis et de lacet.
Les commandes de roue en tangage sont simplement ajoutées à celles de la loi en B point, avec des gains de contrôle optimisés pour assurer une convergence rapide de l'acquisition..
[0038]
Quelle que soit la position du satellite, la rotation à deux fois la pulsation orbitale ω0 induite par la loi en B point garantit que le capteur solaire (non représenté) voit le soleil dans son champ de vue en moins d'une demi-orbite. La première acquisition solaire peut donc toujours être réalisée sur la partie éclairée de l'orbite.
Cette rotation à deux fois la pulsation orbitale s'établit autour de l'axe lié au satellite pour lequel le moment cinétique interne du satellite est aligné avec la vitesse de rotation, donc perpendiculaire au plan de l'orbite. Par un choix approprié de la vitesse de rotation des volants d'inertie et/ou roues de réaction classiquement prévus à bord des satellites, il est possible de choisir la direction du satellite qui reste orientée selon la normale au plan de l'orbite, et cela en ne mettant en oeuvre que le magnétomètre trois axes et les magnéto-coupleurs. Les volants d'inertie sont maintenus ensuite à vitesse constante, pour que l'orientation du moment cinétique interne reste selon l'axe de tangage.
[0017]
Pour éviter les interactions entre les magnéto-coupleurs et le magnétomètre, les mesures et les mises en oeuvre des magnéto-coupleurs sont effectuées par exemple de façon alternée. Puisque la loi en B point utilise une commande fondée sur la dérivée du champ magnétique, les moments magnétiques rémanents constants du satellite ne perturbent pas la mesure.
************************************ Fin de page *******************************