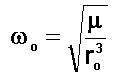|
QUATERNION ET GRADIENT DE GRAVITE SUR UN SATELLITE |
![]()
|
CONTENU : Mis à jour novembre 2002, revu
sept 2011, juin 2013 Cours de mathématiques appliquées à la mécanique |
|
Voir aussi les compléments sur les
quaternions et séquences de rotation
La
gravité, à ne pas confondre avec la pesanteur au sens terrestre du terme, ne
s'applique pas, en général, au centre d'inertie d'un satellite, contrairement à
ce que l'on pense. La ligne d'action est certes décalée d'une quantité infime
par rapport à ce point privilégié, mais cela suffit à crée sur tout corps non
inertiellement sphérique, un couple appelé COUPLE
DU GRADIENT DE GRAVITE. Le
propos n'est pas de démontrer ici son mode de calcul, que vous trouverez sur ce
site ou ailleurs dans de nombreux ouvrages spécialisés.
La
simulation et l'étude du mouvement ne sont pas faciles avec le quaternion
d'attitude. Pour l'interprétation, il faut donc revenir à la représentation
initiale avec les angles classiques, via la matrice de passage P ou son inverse
A.
NB:
il faudra également probablement exprimer certaines composantes de forces à
l'aide du quaternion d'attitude. Un exemple est donné ci dessous.
C'est
le prix à payer pour avoir une intégration numérique paraît-il très stable.
1°) Repères - Notations - Angles
de Cardan:
Nous
intéressons par exemple, au problème de la stabilisation d'un satellite
d'imagerie spatiale, qui doit rester dans une position invariable par rapport
au sol survolé.
O
Xa Ya Za est un repère galiléen, qu'il n'est pas utile de préciser outre
mesure.
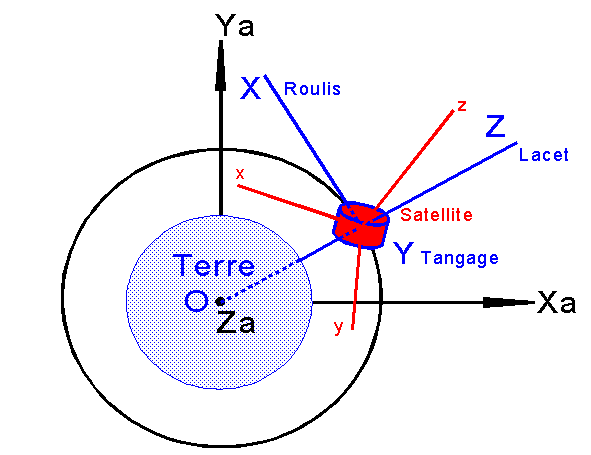
Le
satellite S est en orbite, supposée circulaire, de rayon ro. On
appelle REPERE ORBITAL Ro le repère
d'origine S et d'axes X Y Z, avec :
- X axe
dit de roulis, unitaire de la vitesse orbitale, tangent à
l'orbite.
- Y axe
de tangage, unitaire du moment cinétique, normal à la trajectoire.
- Z axe
de lacet, suivant la géocentrique.
On
désigne par S x y z le repère R, principal d'inertie pour le satellite, avec IR, IT, IL les moments
principaux d'inertie.
Comme
un satellite d'imagerie doit garder ses axes fixes par rapport à ce repère
orbital Ro, nous sommes amenés à définir des angles particuliers, qui pour le
cas d'espèce resteront voisins de 0, tout au long de la vie du satellite, tant
que l'asservissement de stabilisation fonctionne.
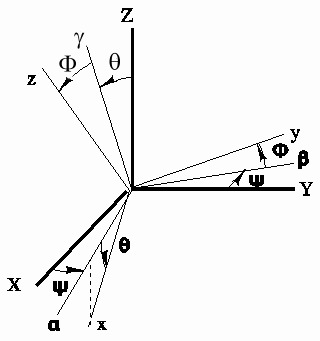
Les
repères sont définis comme suit, après avoir indiqué que l'axe a est la projection sur le plan horizontal X, Y de
l'axe x. La succession de repères est :
XYZ --- Y --> abZ -- q ---> xbg --- F --> xyz
Nous avons ainsi défini les angles
conventionnels, également appelés ANGLES DE CARDAN :
- Lacet y mesuré autour de Z
- Tangage q mesuré autour de b ( voisin de Y lorsque les
angles sont petits)
- Roulis f mesuré autour de x (
voisin de X lorsque les angles sont petits)
La
matrice P de passage de XYZ à xyz s'explicite classiquement :
à
comparer à son expression déduite du quaternion Q=(q0 q1
q2 q3) qui représente la rotation globale composée des 3
rotations élémentaires définies plus haut:
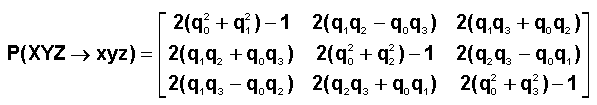
ce
qui permet d'une certaine façon d'exploiter les résultats pour évaluer les
conditions initiales ou les angles en fonction du quaternion.
Exprimé
dans les axes satellites le vecteur rotation instantanée absolue
a pour composantes :
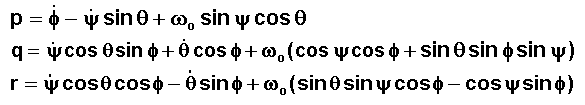
|
où |
|
est la vitesse angulaire orbitale |
Vous
noterez qu'il s'agit de la rotation galiléenne mais que la rotation à annuler
quand on souhaite obtenir un pointage Terre parfait est la rotation relative au
repère orbital de composantes en roulis, tangage et lacet.
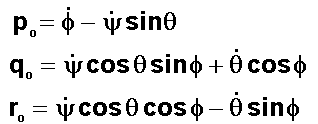
C'est
d'ailleurs cette rotation qu'il faut utiliser dans l'équation différentielle
donnant le quaternion Q de l'attitude dans X Y Z.
2°) Expression du quaternion en
fonction des angles de Cardan :
Un
calcul long, dont j'assume la responsabilité ( car je ne l'ai pas retrouvé
ailleurs pour l'instant) donne un résultat d'une étonnante symétrie, pour
l'expression du quaternion à l'aide des angles de Cardan.
Les
quaternions associés aux rotations élémentaires et à la rotation résultante
sont :
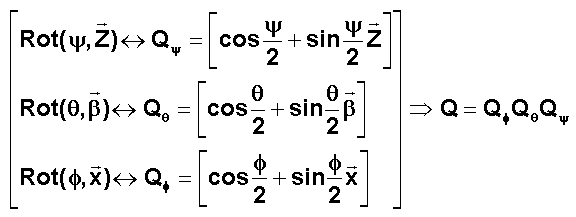
Tous
calculs ( ce serait un excellent entraînement pour le lecteur), effectués dans
le repère fixe de référence ( il faut revenir aux axes X Y Z ), on obtient les
relations remarquables suivantes:
NB
: Certains lecteurs du site me font remarquer qu'on peut aller plus vite, en
conservant les quaternions dans leur repère d'origine. Il faut alors multiplier
ces quaternions en conservant l'ordre des rotations soit calculer Q =Qy.Qq.Qj
Voir un cours spécial dédié à
ce problème du produit ( l'ordre dépendant des repères utilisés)
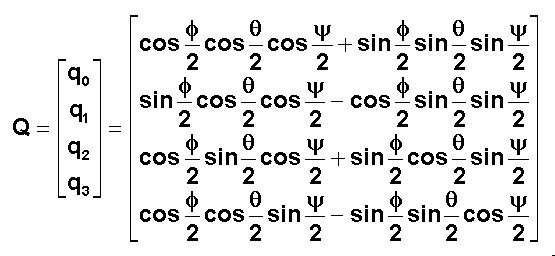
Ce résultat permet une
initialisation ( en position ) sans problème du quaternion Q.
3°) Calcul du gradient de gravité en termes de quaternions :
On
vérifie que le gradient de gravité s'exprime à l'aide du quaternion d'attitude
sous la forme, avec roulis F, tangage q, lacet Y.
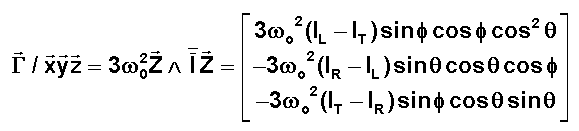
Comme
nous savons calculer les matrices de passage P ( XYZ --> xyz ) et P-1=
tP nous sommes en mesure d'écrire, la dernière ligne de P-1
donne:

et
donc l'expression du couple exact dû au gradient de gravité :
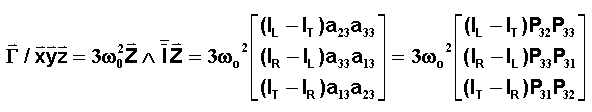
|
On note |
|
Le couple de commande éventuel appliqué en contrôle d'attitude |
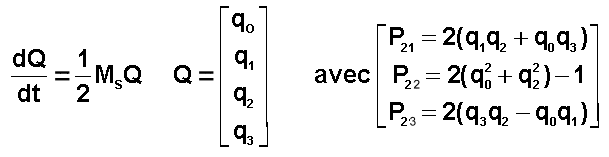
Avec
les notations présentées plus haut, on obtient les équations du théorème du
moment cinétique.
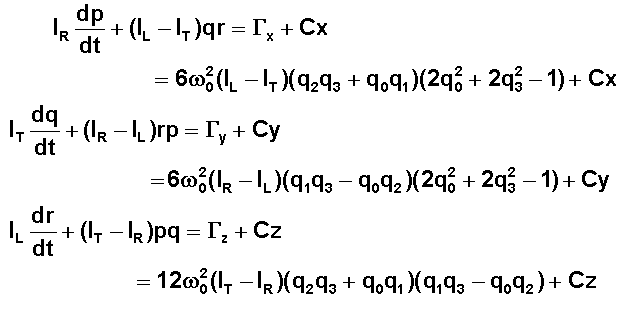
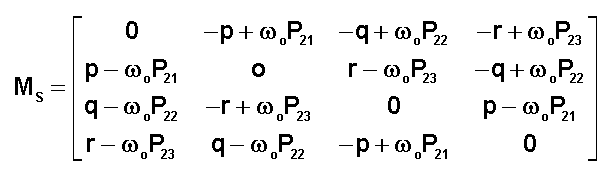
+ CALCULS
D'INITIALISATION ( voir
cours précédent)
III FORMALISATION DU PROBLEME :
On
propose :
·
De
prendre comme variable un vecteur d'état X à 7 coordonnées X = [ p q r qo
q1 q2 q3]
·
D'écrire
le système différentiel sous une forme canonique où F fonction vectorielle ne
dépend que des inerties, de la pulsation orbitale et du vecteur d'état X, ce
qui rendra l'adaptation plus facile pour d'autres applications:
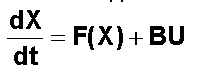
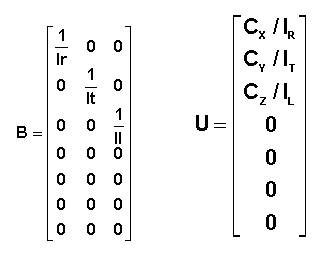
·
B ne
dépend que des inerties et U est le vecteur d'entrée du système, dont les trois
premières composantes sont les couples normalisés en axes satellite.
Le
diagramme fonctionnel pourrait donc être le suivant et constituer un bloc
unique avec une entrée U et une sortie X.
![]()
Guiziou Robert 1994 / révision février 1999 et novembre
2002, sept 2011, juin 2013