REGULATION PAR "EFFET BOUSSOLE"

Rédigé janvier 2014, revu juin 2014

Cette page repose sur un concept technique génial de M Philippe LAURENS, de chez Astrium, qui a déposé un brevet européen:

Date de publication:07.05.2003 Bulletin 2003/19, Numéro de dépôt: 01402710.6,  Date de dépôt: 19.10.2001

Je signale donc, par respect pour l'inventeur, que ma seule contribution à cette page est un essai de mise en forme pédagogique du concept.

NB : Cette page rassemble tous les essais plus ou moins concluants pour arriver à stabiliser le satellite en une seule régulation.

I EXPLICATION DU CONCEPT :

1°) NOTATIONS :

Donnons d'abord une figure pour éclairer la compréhension.

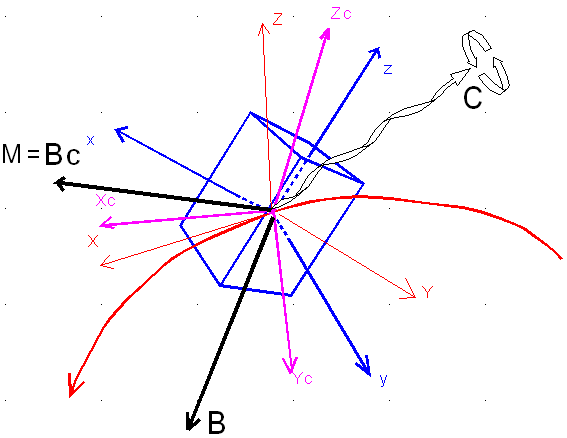
Ro est le repère orbital XYZ

R est le repère satellite x y z

Rc est le repère de consigne, à savoir que le pointage est parfait si R et Rc sont confondus

B est le vecteur champ magnétique existant à l'instant t à la position du satellite

On introduit :

- la matrice de passage P du repère Rc à R, matrice qui se calcule avec le quaternion d'attitude Q représentant une des 2 rotations permettant de passer de Rc à R.

- le vecteur Bc (champ magnétique de consigne ) transformé de B par cette rotation. En clair, à chaque instant, Bc vaut Bc = P. B

2°) LA REGULATION "BOUSSOLE":

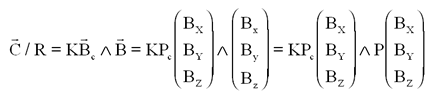
Là est l'idée géniale de Philippe LAURENS est de poser comme moment magnétique de la régulation M = K Bc.

NB : Pour être plus clair, on aurait pu dire qu'il pose un moment magnétique proportionnel à la différence des champs

et qu'au final, économe en calculs,  il omet B qui disparaît dans le produit vectoriel

Que peut-on en déduire? Un résultat très simple, le couple magnétique C à tendance à rapprocher la consigne magnétique Bc du vecteur B réel.

Donc Bc ---> B, examinons mathématiquement comment le traduire ( quand Bc est colinéaire ou opposé à B ). Avec les matrices des composantes on a après passage à la limite :

Ce qui permet d'affirmer que P est une matrice de passage correspondant à une rotation qui conserve B, donc d'axe B, ou que B est une direction propre de P ou encore que le quaternion associé peut s'écrire ( utilisant un angle a indéterminé )

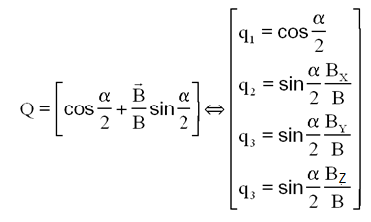
NB : Pour a = 0 ou a = 2p, on peut donc avoir tout à fait par hasard, le satellite bien pointé Terre ou à l'envers pointé zénith. Dans ce cas là et seulement dans ce cas on a :

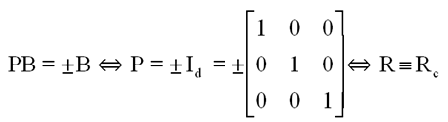
Physiquement le repère satellite R coïnciderait avec celui de consigne Rc ou lui serait symétrique, dans une symétrie de centre 0, et donc la régulation serait parfaite ( à une symétrie près ). Le problème à résoudre sera celui de la maîtrise de la rotation autour de B

REMARQUE : Le résultat fait clairement apparaître avec le signe + ou - que le pointage peut s'achever en bon alignement ou à " l'envers" avec tous les axes à 180° du pointage souhaité.

Donc, avec 3 magnétocoupleurs, sans roue, ce risque subsiste, alors qu'avec 2 magnétocoupleurs et une roue, l'effet d'alignement gyroscopique devrait supprimer ce risque.

Le nom d'"EFFET BOUSSOLE" vient du fait que le champ magnétique sert de repère pour aligner Bc sur lui, comme quand on utilise une boussole. 

" Exactement comme un marcheur ( le satellite ) qui s'oriente en tenant  à la main devant lui une carte sur laquelle il est indiqué la direction du nord ( consigne Bc ), la boussole qu'il tient à la main  lui donne B ( champ existant ). Que fait-il alors? Il tourne, de telle manière que l'aiguille de la  boussole vienne s'aligner sur le nord de la carte." Donc il amène Bc sur B.

Un dessin illustre le commentaire

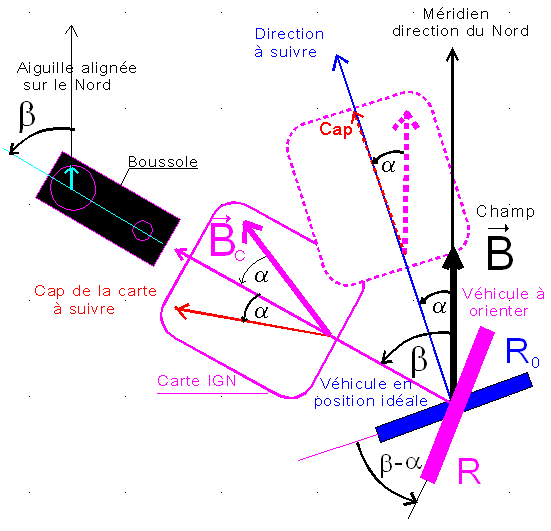
Mon point de vue : Le raisonnement est volontairement simplifié avec ( pour un marcheur ) un mouvement et un guidage plan. Le satellite est R comprenant la carte IGN et le corps de la boussole qui lui sont liés. La configuration idéale du satellite ( bon cap ) est en bleu c'est R0. 

La direction de consigne est Bc qui se déduit de B par la rotation d'angle b-a

M. LAURENS indique que la direction de consigne en axes satellite est la direction du champ magnétique ( rose en pointillés) lorsque le mobile rose ( R ) vient se superposer au mobile bleu, en position idéale. Cette position est donc mémorisée, affichée dans le satellite rose, pour donner le vecteur de consigne Bc ( bien évidemment cette consigne varie, puisque le satellite est en rotation ).

En effet, en cherchant à aligner Bc sur B, donc en tournant de l'angle b-a, on amène le mobile R en configuration idéale.

On peut en déduire que Bc est l'image de B par la rotation qui amène R0 sur R, la matrice de passage est P. 

DETAILS DE CALCULS : 

On notera donc que Bc exprimé dans le repère R a donc les mêmes composantes que B exprimé dans R0. Ou encore avec les notations maintenant classiques XYZ pour le repère R0 et xyz pour le repère satellite, on a:

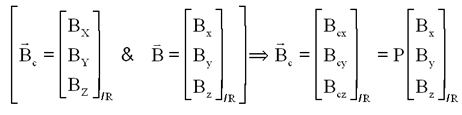
En clair, le couple de commande, sans considération de saturation des bobines, s'écrit, au choix:

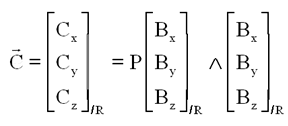ou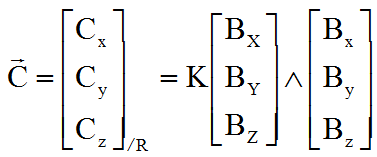

Remarque importante :

Il est évident que le mot " consigne " suppose que la quantité qui la représente est connue ou estimée au mieux à chaque instant. Dans notre cas c'est le champ magnétique local.

Donc 2 façons de calculer Bc :

1 - Connaître à bord le champ en axes satellite et connaître son attitude, de manière à avoir P et B donc Bc = P*B'. Sont donc nécessaires comme équipements, un magnétomètres 3 axes et une restitution d'attitude.

2 - Emporter un modèle de champ magnétique analytique ou tabulé, genre modèle IGRF, ce qui suppose qu'une restitution d'orbite assez précise est possible à bord de manière à fournir une estimation de position au modèle IGRF. Voir page dédiée.

Dans ce cas là Bc a pour composantes dans Rc ( B_X B_Y B_Z ) donc celles de B dans le repère orbital R0.

II EXPLOITATION DU PROCEDE :

1°) NOTION DE REPERE DE CONSIGNE :

Dans le cas qui nous intéresse, le satellite est idéalement orienté si le repère orbital R0 et le repère satellite R sont confondus.

Le repère à asservir est R, le repère à rejoindre est R0, d'où son nom de repère de consigne, plus généralement noté Rc.

Dans notre cas la consigne étant R0, elle se traduit dans le cas d'une régulation idéale, par la convergence B --> Bc 

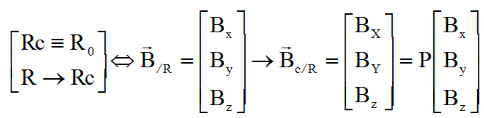
GENERALISATION :

Pour des applications spécifiques, on peut avoir besoin de pointer un axe particulier du satellite dans une direction bien précise. Le repère de consigne Rc est alors différent de R0. On note les matrices de passage, Pc de R0 (repère orbital ) vers Rc (repère de consigne ), P de R0 vers R ( repère satellite ) :

Pour les simulations, les calculs de couples se font en repère satellite R. Rappelons les conventions d'écriture des composantes du champ B ou de la consigne Bc (Le champ magnétique de consigne est Bc dont les composantes en axes satellite sont les mêmes que celles de B dans Rc ) 

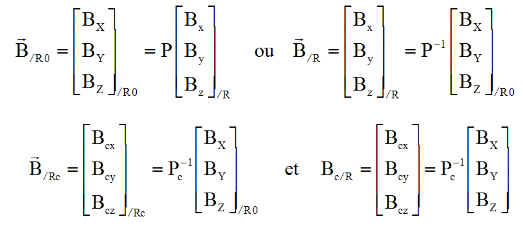
Le couple de commande se calcule alors  en axes satellite par :

2°) ACTIONS POSSIBLES DU CONTRÔLE :

M LAURENS souligne les avantages du concept :

- Il permet la réduction des vitesses

- L'acquisition d'un pointage Terre

- La conservation de cette attitude à quelques degrés près

Il insiste sur la grande souplesse laissée par le choix du repère de consigne, choix qui permet ( je ne l'ai pas encore vérifié ou simulé ):

- De choisir tout pointage prédéterminé, Terre Soleil ...

- D'opérer des basculements notamment en tangage.

a) Exemple 1: pointage zénith

On souhaite que le repère satellite xyz coïncide avec le repère orbital XYZ. Le repère de consigne est XYZ ==> Bc=[BX BY BZ ]^T

b) Exemple 2: pointage nadir ou retournement autour de X

On souhaite que le repère satellite x y z coïncide avec le repère ( Xc=X, Yc=-Y, Zc= -Z ). Le repère de consigne est XcYcZc ==> Bc=[BX -BY -BZ ]^T

c) Exemple 3: retournement autour de Z

Le repère satellite x y z doit coïncider avec Xc = -X  Yc=-Y  Zc=-Z   Le repère de consigne est XcYcZc ==> Bc=[-BX -BY BZ ]^T

d) Exemple 4: retournement autour de Y

Le repère satellite x y z doit coïncider avec Xc = -X  Yc=Y  Zc=-Z   Le repère de consigne est XcYcZc ==> Bc=[-BX BY -BZ ]^T

d) Exemple 5: attitude fixe quasi inertielle

Le satellite doit rester d'orientation fixe dans le plan orbital. Voir survie quasi inertielle

e) Exemple 6: alignement d'une normale aux panneaux disposés sur une des faces satellite, sur l'unitaire du soleil.

Pour un mode survie, le satellite doit voir le soleil normalement aux panneaux. Il faut définir un repère, par exemple avec y vers le soleil d'unitaire Us. Le repère de consigne est à choisir, Xc? Yc=Us, Zc? Bc=[B.Xc, B.Us B.Zc]^T

etc....

f) Pour information : Accompagné d'un terme supplémentaire, la régulation de Laurens peut mettre en spin à une vitesse donnée, autour d'un axe donné quelconque. Voir étude pour l'optimisation de l'énergie.

3°) TECHNOLOGIES NÉCESSAIRES :

Je cite M LAURENS :

[0008] Une caractéristique remarquable du procédé de contrôle d'attitude suivant l'invention, qu'on peut qualifier de pilotage en « mode boussole », est l'utilisation d'un  actionnement magnétique semi-passif, nécessitant uniquement des magnéto-coupleurs permettant une action suivant 3 axes, un magnétomètre également 3 axes, un modèle magnétique disponible à bord et une estimation initiale de la position du satellite dans un repère terrestre. 

- 3 magnétocoupleurs ou ( pour nous peut-être, 2 magnétocoupleurs et une roue )

- Un magnétomètre 3 axes, dont M LAURENS précise, je le cite :

[0001] La présente invention concerne les procédés de contrôle de l'attitude d'un satellite placé sur une orbite suffisamment basse pour que l'intensité du champ magnétique terrestre autorise une mesure d'attitude à l'aide d'un magnétomètre trois axes (c'est à dire fournissant une mesure de module et d'orientation dans un référentiel lié au satellite) et permette une commande de modification d'attitude par interaction de magnéto-coupleurs portés par le satellite avec le champ magnétique terrestre.

- Un modèle magnétique, encore faut-il préciser, en ce qui me concerne, ce qu'il est nécessaire de connaître et ce qu'il met à disposition  

- Une estimation initiale de la position du satellite en repère terrestre, je suppose pour générer la première consigne, le calculateur se chargeant ensuite d'estimer l'attitude et la position future, du moins dans la première phase.

4°) AMELIORATIONS PREVUES PAR M LAURENS :

C'est en somme comme pour une régulation PD ( Proportionnelle - Dérivée ), au terme dit de rappel élastique, on peut ajouter une dissipation d'énergie qui comme toutes les dissipations nécessite un terme complémentaire proportionnel à la dérivée. Il propose ainsi une loi normalisée avec le module de B

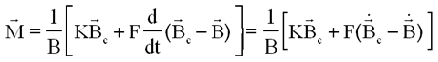
5°) AUTRE FINESSE DANS LE CALCUL DU MOMENT MAGNETIQUE :

Bien évidemment la création d'un moment magnétique demande de l'énergie, donc il ne faut générer que le moment magnétique nécessaire. Or la formule ci-dessus contient vraisemblablement un terme colinéaire à B et ce terme est strictement inutile dans la fabrication du couple, donc M LAURENS élimine cette composante, ce qui donne pour le calcul définitif du moment magnétique:

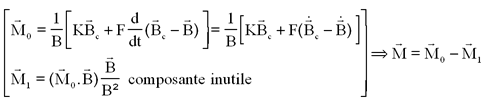
Finalement, pour les programmations futures on utilisera les relations suivantes pour le moment magnétique et le couple généré

LIMITATION PROPORTIONNELLE  DES BOBINES, DANS LE CAS D'UNE RÉGULATION SANS ROUE :

On va donc calculer le moment magnétique M dans les axes x y z et obtenir ainsi mx, my, mz. Comme le préconise M LAURENS, ce que nous avions déjà découvert aussi, il faut respecter la spécification de maximum de puissance des bobines.

Pour l'instant les nôtres sont limitées à 0.2 Am², que nous appelons Mmax, ce qui conduit au choix proportionnel suivant :

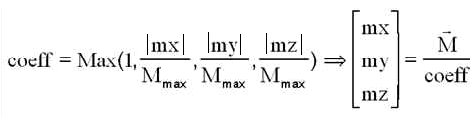
Ainsi si l' une des bobines dépasse le seuil maximum, l'écrêtage se fait proportionnellement et si toutes sont en dessous, on garde les valeurs.

NB : La présence du 1 dans le calcul du maximum indique que les bobines ne sont pas forcées ( du moins une au plus à chaque instant ) à travailler à leur limite. 

LIMITATION PROPORTIONNELLE  DES BOBINES, DANS LE CAS D'UNE RÉGULATION AVEC ROUE :

Lorsque le couple de commande est calculé avec à la fois des magnétocoupleurs et une roue, le contrôle de saturation porte donc simultanément suir les magnétocoupleurs et la roue.

Une réduction proportionnelle est donc envisagée en cas de dépassement:

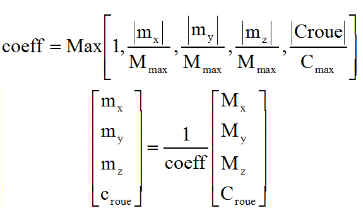
III CHOIX ET TEST DES SIMULATIONS  :

1°) PREMIÈRE OPTION A 3 MAGNETOCOUPLEURS, ROUE ARRÊTÉE ( ou sans roue ):

C'est la régulation de base de M Philippe LAURENS

NB 2: Cette option fait l'objet de la  simulation regbous1  avec champ mesuré pulsé, le calcul des moments magnétiques éventuellement plafonnés est réalisé par la fonction laurens0.m    tout est dans /../ regbous0.

Retrouver les fichiers

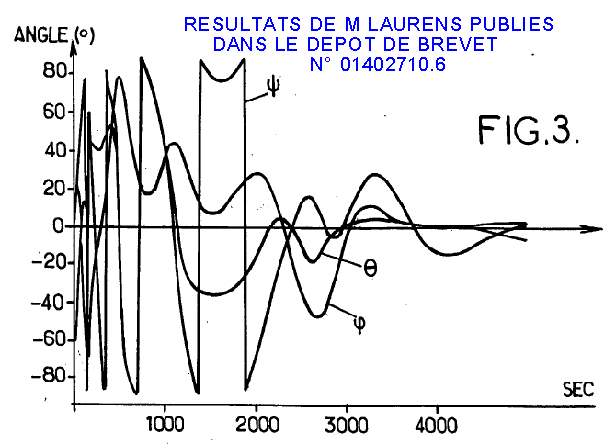
Les vitesses sont bien réduites mais, le tangage reste rebelle et les angles ne sont pas stabilisés. Le résultat angulaire est aléatoire. On pouvait s'y attendre, car la rotation autour de B ne peut être contrée, en effet aucun couple d'axe B ne peut être généré magnétiquement.

M LAURENS présente une courbe montrant qu'en utilisant une roue de réaction, il arrive à stabiliser à 5° près les 3 angles. Je le cite, en recopiant fidèlement ce qu'il écrit :

Comme la mise en oeuvre de la roue en [0027 ] n'est pas précisée, j'essaye plusieurs solutions. Cependant en [0028 ] il semble que la roue soit sur l'axe de tangage, sans que son mode d'utilisation soit net ( comme réaction à vitesse commandée ou à vitesse constante, mais alors laquelle? )

 IV LA SOLUTION :

**************************  Fin de page ***************************