CHAMP MAGNÉTIQUE : MODÈLE IGRF
ÉQUIPEMENTS ASSOCIES AU CHAMP
![]()
|
II RÉCUPÉRATION DES COEFFICIENTS DU MODÈLE IV ANNEXES DES FONCTIONS ADAPTÉES
|
|
Rédigé mai 2014
![]()
L'auteur de cette page n'est pas du tout un spécialiste du champ magnétique et ne propose les informations qui suivent, comme synthèse de ce qu'il a lu pour donner à un satellite les moyens d'utiliser au mieux des magnétocoupleurs utilisés en contrôle d'attitude ( SCA ). Dans le cas présent, ce sera pour un nanosatellite.
Les simulations du SCA ont été réalisées avec un champ analytique simple, pour étudier la faisabilité d'un contrôle avec une roue et 3 magnétocoupleurs au plus. Le vol réel devrait, le choix reste à faire, emporter un modèle de champ magnétique ne nécessitant qu'une estimation de la position du satellite par rapport à la Terre.
Un modèle IGRF ( International Geomagnetic Reference Field ) stocké à bord, est pressenti.
La précision dépend du nombre de termes retenus dans un développement en série de fonctions harmoniques du potentiel associé au champ magnétique, duquel on déduit le champ B par un gradient négatif. Il est important de retenir que les dérivées vont donner les composantes sur les axes unitaires associés à chaque paramètre:
- r rayon vecteur est associé à la verticale orientée zénith, F longitude est associée à l'unitaire tangent à un parallèle de la terre, donc vers l'Est , q la colatitude est associée à la tangente au méridien, mais orientée vers le Sud, avec la latitude, c'aurait été le Nord géographique.
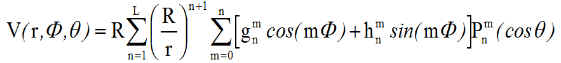
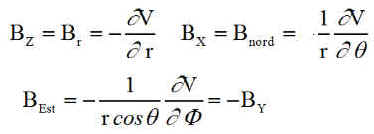
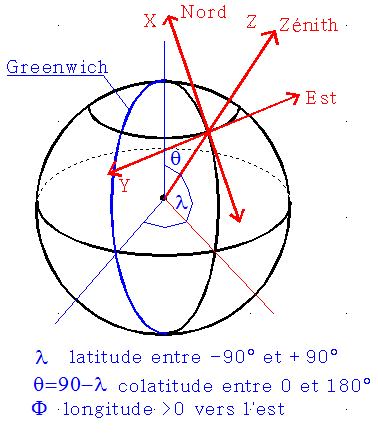
- R est le rayon terrestre, adopté à 6371.2 km
- F est la longitude de 0° à + 360° mesurée positivement vers l'Est depuis Greenwich
- q est la 'colatitude géocentrique' ( q = 90 - l ) mesurée depuis le pôle nord de 0° à 180° q = 90 - l
- r est le rayon vecteur de la position satellite
- Pnm est le polynôme de Schmidt normalisé associé au polynôme de Legendre de degré n et d'ordre m. N'étant pas un spécialiste de ces polynômes, je n'en dirai pas plus, vous laissant le choix des sites à consulter. Pour moi, l'essentiel est d'arriver à programmer le champ magnétique IGRF.
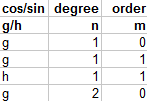
- Les coefficients gnm et hnm avec m<=n sont donnés par des tables revues régulièrement avec une validité de 5 ans et une correction linéaire par des termes séculaires ( notés SV ).
1°) COMMENTAIRES SUR LA TABLE :
On trouvera un fichier texte des coefficients --> http://www.ngdc.noaa.gov/IAGA/vmod/igrf.html
Ou une feuille Excel de ces mêmes coefficients -- > http://www.ngdc.noaa.gov/IAGA/vmod/igrf11coeffs.xls
Exemple de table sur Excel. Une fois le tableau Excel sous les yeux, on peut y voir les colonnes de coefficients, de 5 ans en 5 ans depuis 1900 jusqu'à 2010. La dernière colonne notée SV donne la variation séculaire moyenne à prévoir sur les 5 dernières années à venir. Elle permet d'anticiper sur les valeurs futures des coefficients. Donnons un exemple :
| # 11th Generation International Geomagnetic Reference Field Schmidt semi-normalised spherical harmonic coefficients, degree n=1,13 | ||||||||||||||||||
| # in units nanoTesla for IGRF and definitive DGRF main-field models (degree n=1,8 nanoTesla/year for secular variation (SV)) | ||||||||||||||||||
 |
.........
......... ......... |
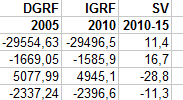 |
SV est la variation annuelle sur le coefficient précédent : g1,0(2010) = -29496.5 --> g1,0(juin 2014) = g1,0(2010)+4.5*11.4= -29445,2
NB : Apparemment SV n'est valable que pour la période à venir, on peut le constater en passant de 2005 à 2010, si on utilise SV, il y a une petit écart par rapport au calcul d'interpolation. De même, la colonne de l'année est le résultat le plus sûr connu et établi par une équipe de scientifiques spécialement chargée de la tenue de la table.
ÉLABORATION D'UNE LOGIQUE PROGRAMMEE :
Ne pouvant directement utiliser les nombreuses sources de logiciels avec une version trop ancienne de Matlab, je me suis attaqué à l'adaptation des routines que j'ai téléchargées.
Après une série de manipulations des fichiers de données, j'ai pu construire une logique qui fonctionne:
a) igrfnum1.xls est le tableau de 26 colonnes sur 196 lignes avec :
Ligne 1: n m puis les dates se terminant par 2010-15 pour les SV
Colonnes 1 et 2 : les valeurs de n et m
b) igrfnum2.m qui fournit à l'espace Matlab le tableau des coefficients sous la forme de la matrice M_igrf11 ( 196 lignes, 26 colonnes )
c) function [gh,xdate]=GH_coeff(M_igrf11) lit la matrice M_igrf11 et stocke les coefficients gh dans un fichier coeff_GH.mat.
Au total ( 195 x 23 ), soit 3485 coefficients maximum, en fait le programme n'en retient que 3255.
d) function [B]=igrf11(fyears,alt,nlat,elong) fournit en Teslas les composantes du champ avec :
fyears la date en année décimale
alt l'altitude sol en km
nlat la latitude en degrés > vers le Nord
elong la longitude en degrés > vers l'Est
En sortie B = [B_North; B_East; B_up] (Teslas) , attention, c'est dans le repère terrestre N(Nord), E(Est), Z (Zénith), il faudra pour les applications ramener ces composantes en repère orbital, puis éventuellement en repère satellite.
II RÉCUPÉRATION DES COEFFICIENTS DU MODÈLE :
Ne sachant pas qu'elle sera la date d'utilisation du modèle IGRF, j'ai choisi de créer pour mon usage personnel le modèle de l'année 2010.
1°) RÉCUPÉRATION DE LA TABLE EXCEL complète : Elle se présente ainsi, je ne donne que les 4 premières lignes, par exemple année 1900 :
|
g/h |
n |
m |
1900 |
|
g |
1 |
0 |
-31543 |
|
g |
1 |
1 |
-2298 |
|
h |
1 |
1 |
5922 |
|
g |
2 |
0 |
-677 |
Il faut comprendre :
- g est le coefficient gnm avec g10= -31543 nT, g11= -2298 nT, g20= -677 nT
- h est le coefficient hnm avec h11= 5922 nT etc...
Il y a comme ceci 195 lignes et 4 colonnes et ceci pour toutes les années jusqu'à 2010, par pas de 5 années.
2°) MANIPULATION DE LA TABLE ET EXTRACTION DE L'ANNÉE 2010 PAR EXEMPLE :
A = xlsread('filename')
returns numeric data in array A from the first sheet in Microsoft
Excel spreadsheet file named filename. xlsread ignores
leading rows or columns of text. However, if a cell not in a leading row or
column is empty or contains text, xlsread puts a NaN
in its place in A.
Grâce à EXCEL, j'ai pu par quelques manipulations simples sur les chaînes de caractères, garder l'année 2010, avec ses 195 lignes et 4 colonnes, le tout stocké dans un fichier de données Matlab IGRF2010.MAT où la variable est une matrice M
|
1 |
1 |
0 |
-29496 |
|
1 |
1 |
1 |
-1585 |
|
0 |
1 |
1 |
4945 |
|
1 |
2 |
0 |
-2396 |
|
1 |
2 |
1 |
3026 |
|
0 |
2 |
1 |
-2707 |
|
,,,,,,, |
,,,,, |
,,,,, |
|
|
1 |
13 |
12 |
0 |
|
0 |
13 |
12 |
0 |
|
1 |
13 |
13 |
0 |
|
0 |
13 |
13 |
0] |
NB1 : Dans la première colonne j'ai choisi le code 1 pour le 'g' et le code 0 pour le 'h'. Ce sera donc facile à repérer.
NB2 : Le fichier IGRF2010.MAT se présente sous la forme d'une matrice de 195x4
3°) EXÉCUTION DU PROGRAMME GENERAL :
Après une série de manipulations des fichiers de données, j'ai pu construire une logique, que je n'ai pas inventée, mais récupérée sur Internet et adaptée à mon logiciel Matlab ancien , à partir des sources IGRF-11 coefficients (text file, excel spreadsheet)
et essentiellement aussi sur http://www.mathworks.com/matlabcentral/fileexchange/28874-igrf-magnetic-fiel site sur lequel vous pouvez télécharger les routines.
Pour ce qui est des miennes, les voici:
a) igrfnum1.xls est le tableau de 26 colonnes sur 196 lignes avec :
Ligne 1: n m puis les dates se terminant par 2010-15 pour les SV
Colonnes 1 et 2 : les valeurs de n et m
b) igrfnum2.m qui fournit à l'espace Matlab le tableau des coefficients sous la forme de la matrice M_igrf11 ( 196 lignes, 26 colonnes )
c) function [gh,xdate]=GH_coeff(M_igrf11) lit la matrice M_igrf11 et stocke les coefficients gh dans un fichier coeff_GH.mat.
Au total ( 195 x 23 ), soit 3485 coefficients maximum, en fait le programme n'en retient que 3255 utiles, pour une question de précision ( soit avec 13 coefficients, soit avec 10 ).
d) function [B]=igrf11(fyears,alt,nlat,elong) fournit en Teslas les composantes du champ avec :
fyears la date en année décimale
alt l'altitude sol en km
nlat la latitude en degrés > 0 vers le Nord
elong la longitude en degrés > 0 vers l'Est
En sortie B = [B_North; B_East; B_up] ( Teslas) , attention, c'est dans le repère terrestre N, E, Z (zénith) il faudra plus tard, pour les applications, ramener ces composantes en repère orbital, puis en repère satellite.
NB 1 : On retiendra que ce modèle suppose connue la position du satellite ( altitude, latitude et longitude ) ou du moins une bonne estimation de sa position.
NB 2 : Le jour où on connaîtra les coefficients pour 2015 et les SV pour les 5 années suivantes, il faudra encore adapter les programmes.
On n'est jamais assez prudent, donc je vérifie que mes routines donnent bien le même résultat que celles que j'ai téléchargées avant de les adapter.
Ce site http://omniweb.gsfc.nasa.gov/vitmo/igrf_vitmo.html propose un calcul ponctuel
Essayons de comparer les valeurs du champ sur un méridien, avec mes fonctions, ceci en a) et b) puis avec des routines dédiées sur Internet en c) et d)
a) Avec notre modèle simplifié : la longitude n'y jouant aucun rôle, avec un champ invariant par rotation autour de l'axe des pôles l est la latitude Nord.
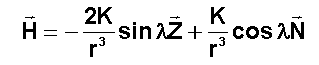
![]()
K= 6.413 1021 A-m2
b) Avec le modèle IGRF11 : Prenons 5 points sur le méridien de Greenwich, r = 6378+817 = 7295 km, calculs en 2010, longitude 0°. Résultats en Teslas.
| MODELES\LATITUDE | -90° | - 45° | 0° | 45° | 90° |
| ANALYTIQUE
Adopté dans les simulations |
BX=0
BY=0 BZ= 4.1517 e-5 |
BX=1.4678 e-5
BY=0 BZ=2.9356 e-5 |
BX=2.0758 e-5
BY=0 BZ=0 |
BX=1.4678 e-5
BY=0 BZ=-2.9356 e-5 |
BX=0 BY= 0 BZ= - 4.1517 e-5 |
| IGRF Modèle adapté par mes soins, B=igrf11(2010,817,nlat,0) utilise coeff_GH.mat | BX=0.842 e-5 BY=-0.55 e-5 BZ=-3.675 e-5 |
BX=0.861 e-5 BY=-0.343 e-5 BZ=-1.764 e-5 |
BX=1.879 e-5 BY=-0.222 e-5 BZ=-0.826 e-5 |
BX= 1.621 e-5 BY=0.068 e-5 BZ=2.798 e-5 |
BX=0.086 e-5 BY= -0.07 e-5 BZ= 4.071 e-5 |
|
Vérifications avec le site |
BX=0.84213 e-5 BY=-0.56654 e-5 BZ=-3.67457 e-5 |
BX=0.8606 e-5 BY=-0.343 e-5 BZ=-1.76419 e-5 |
BX=1.87857 e-5 BY=-0.22187 e-5 BZ=-0.82644 e-5 |
BX= 1.62115 e-5 BY=0.0683 e-5 BZ=2.79846 e-5 |
BX=0.08614 e-5 BY= -0.06922 e-5 BZ= 4.0706 e-5 |
Commentaires : La vérification du modèle IGRF est excellente et prouve que l'adaptation des routines fonctionne à 100%. Pour ce qui est du modèle analytique simple, l'erreur sur les composantes les plus grandes à environ 10 à 20 % en moyenne. Pour une latitude de - 45° le modèle analytique est assez loin du modèle IGRF.
NB : Il me semble qu'il y a une erreur et que dans la fonction B_up doit être changé en B_down. La preuve est donnée par B_up <0, au pôle Nord ce qui signifie que le champ serait vertical ascendant, alors qu'il rentre vers la terre. D'ailleurs le site
http://omniweb.gsfc.nasa.gov/vitmo/igrf_vitmo.html
Donne bien une composante B_down
Téléchargement de mes routines
1°) MAGNETOMETRE :
- Un magnétomètre uniaxe est un équipement qui donne la composante du champ magnétique local, au voisinage du véhicule spatial, sur l'axe de mesure de l'appareil.
- Un magnétomètre 3 axes fournit à bord d'un engin spatial, le vecteur champ magnétique local, dans les axes privilégiés du véhicule.
Remarque : si un modèle de champ magnétique est embarqué, et si la position du satellite est précise, il est clair que le module du champ magnétique est connu. Donc, on pourrait se contenter de 2 magnétomètres pour connaître les 3 composantes. En pratique, la troisième mesure est redondante mais utile en cas de panne d'un des 3 appareils.
Conditions de fonctionnement :
À l'aide de la carte du champ magnétique terrestre et de 3 magnétomètres (en théorie, 2 suffisent, si on connaît précisément le module du champ magnétique terrestre au point et à l'instant considéré), et connaissant la position sur orbite, on peut obtenir une information (incomplète à une rotation près autour du vecteur champ magnétique, en effet si le repère d'expression des composantes tourne autour de B, les composantes restent inchangées ) sur l'attitude du véhicule spatial. Ces instruments sont sensibles aux perturbations électromagnétiques générées par les équipements des véhicules spatiaux (en particulier les actuateurs à couple magnétique) et ils sont donc souvent éloignés des dispositifs perturbateurs (par exemple en les plaçant à l'extrémité d'une perche fixée au corps du vaisseau spatial). Les magnétomètres dans les SCAO peuvent aussi être utilisés pour déterminer précisément le champ magnétique terrestre afin de calculer la commande sur des actuateurs à couple magnétique (magnétocoupleurs). L'intensité du champ magnétique décroissant rapidement avec l'altitude, l'usage de magnétomètres pour la détermination de l'attitude est réservé aux satellites en orbite basse.
- Adresse pour un calcul ponctuel de composantes du champ magnétique --> http://wdc.kugi.kyoto-u.ac.jp/igrf/point/index.html
- Chez Matlab, l'ensemble des routines pour calculer le champ : http://www.mathworks.com/matlabcentral/fileexchange/34388-international-geomagnetic-reference-field--igrf--model/content/igrf.m
- D'autres modèles concurrents http://www.ngdc.noaa.gov/IAGA/vmod/candidatemodels.html
V ANNEXES DES FONCTIONS ADAPTEES :
function [B]=igrf11syn(fyears,alt,nlat,elong)
%****************************************************
% Direct conversion of igrf11_f to MATLAB
% USAGE: [B]=igrf11syn(fyears,alt,nlat,elong)
%
% INPUT: fyears = date in fractional years e.g. 1909.5
% alt = altitude in (km)
% nlat = latiude positive north (deg)
% elong = longitude positive east (deg)
% OUTPUT:
% B = [B_North; B_East; B_up] (nano Teslas)
%
% Conversion written by
% Charles L. Rino
% Rino Consulting
% September 27 2010/October 3 2010
% crino@mindspring.com
%
% CHANGES
% date replaced by fyears
% colat replaced by nlat
% isv and itype preset to 0 and 1, respectively
% output changed from [x,y,z,f] to non-redundant vector B=[x; y; z];
%The following text is from the fortran comment lines:
%
% This is a program for synthesising geomagnetic field values from the
% International Geomagnetic Reference Field series of models as agreed
% in December 2009 by IAGA Working Group V-MOD.
% It is the 11th generation IGRF, ie the 10th revision.
% The main-field models for 1900.0, 1905.0,..1940.0 and 2010.0 are
% non-definitive, those for 1945.0, 1950.0,...2005.0 are definitive and
% the secular-variation model for 2010.0 to 2015.0 is non-definitive.
%
% Main-field models are to degree and order 10 (ie 120 coefficients)
% for 1900.0-1995.0 and to 13 (ie 195 coefficients) for 2000.0 onwards.
% The predictive secular-variation model is to degree and order 8 (ie 80
% coefficients).
%
% Options include values at different locations at different
% times (spot), values at same location at one year intervals
% (time series), grid of values at one time (grid); geodetic or
% geocentric coordinates, latitude & longitude entered as decimal
% degrees or degrees & minutes (not in grid), choice of main field
% or secular variation or both (grid only).
% Recent history of code:
% Aug 2003:
% Adapted from 8th generation version to include new maximum degree for
% main-field models for 2000.0 and onwards and use WGS84 spheroid instead
% of International Astronomical Union 1966 spheroid as recommended by IAGA
% in July 2003. Reference radius remains as 6371.2 km - it is NOT the mean
% radius (= 6371.0 km) but 6371.2 km is what is used in determining the
% coefficients.
% Dec 2004:
% Adapted for 10th generation
% Jul 2005:
% 1995.0 coefficients as published in igrf9coeffs.xls and igrf10coeffs.xls
% now used in code - (Kimmo Korhonen spotted 1 nT difference in 11 coefficients)
% Dec 2009:
% Adapted for 11th generation
%
% INPUT
% isv = 0 if main-field values are required
% isv = 1 if secular variation values are required
% date = year A.D. Must be greater than or equal to 1900.0 and
% less than or equal to 2015.0. Warning message is given
% for dates greater than 2010.0. Must be double precision.
% itype = 1 if geodetic (spheroid)
% itype = 2 if geocentric (sphere)
% alt = height in km above sea level if itype = 1
% = distance from centre of Earth in km if itype = 2 (>3485 km)
% colat = colatitude (0-180)
% elong = east-longitude (0-360)
% alt, colat and elong must be double precision.
% OUTPUT
% x = north component (nT) if isv = 0, nT/year if isv = 1
% y = east component (nT) if isv = 0, nT/year if isv = 1
% z = vertical component (nT) if isv = 0, nT/year if isv = 1
% f = total intensity (nT) if isv = 0, rubbish if isv = 1
% B = [x; y; z]
%
% To get the other geomagnetic elements (D, I, H and secular
% variations dD, dH, dI and dF) use routines ptoc and ptocsv.
%
% Adapted from 8th generation version to include new maximum degree for
% main-field models for 2000.0 and onwards and use WGS84 spheroid instead
% of International Astronomical Union 1966 spheroid as recommended by IAGA
% in July 2003. Reference radius remains as 6371.2 km - it is NOT the mean
% radius (= 6371.0 km) but 6371.2 km is what is used in determining the
% coefficients. Adaptation by Susan Macmillan, August 2003 (for
% 9th generation) and December 2004.
% 1995.0 coefficients as published in igrf9coeffs.xls and igrf10coeffs.xls
% used - (Kimmo Korhonen spotted 1 nT difference in 11 coefficients)
% Susan Macmillan July 2005
%************************************************************************************
global gh
%%%%%%%%%%%Variable Changes:
isv=0;
itype=1;
colat=90-nlat;
%****************************************************
cl=NaN*ones(1,13);
sl=NaN*ones(1,13);
x = 0;
y = 0;
z = 0;
if fyears < 1900 || fyears > 2020
error('Date >=1900 & <=2020')
end
if fyears > 2015
warning('on',' This version of IGRF intended for use to only to 2015 \n')
end
if fyears <2010
t = 0.2*(fyears - 1900.0);
ll = floor(t);
one = ll;
t = t - one;
if fyears<1995.0
nmx = 10;
nc = nmx*(nmx+2);
ll = nc*ll;
kmx = (nmx+1)*(nmx+2)/2;
else %1995<=fyears<2010
nmx = 13;
nc = nmx*(nmx+2);
ll = floor(0.2*(fyears - 1995));
ll = 120*19 + nc*ll;
kmx = (nmx+1)*(nmx+2)/2;
end
tc = 1-t;
if isv==1
tc = -0.2;
t = 0.2;
end
else %>= 2010
t=fyears-2010;
tc =1;
if isv==1
t=1;
tc=0;
end
ll = 2865;
nmx = 13;
nc = nmx*(nmx+2);
kmx = (nmx+1)*(nmx+2)/2;
end
r = alt;
one = colat*0.017453292;
ct = cos(one);
st = sin(one);
one = elong*0.017453292;
cl(1) = cos(one);
sl(1) = sin(one);
cd = 1.0;
sd = 0.0;
l = 1;
m = 1;
n = 0;
if itype==1 %Skip if itype==2
% Conversion from geodetic to geocentric coordinates (using the WGS84 spheroid)
a2 = 40680631.6;
b2 = 40408296.0;
one = a2*st*st;
two = b2*ct*ct;
three = one + two;
rho = sqrt(three);
r = sqrt(alt*(alt + 2.0*rho) + (a2*one + b2*two)/three);
cd = (alt + rho)/r;
sd = (a2 - b2)/rho*ct*st/r;
one = ct;
ct = ct*cd - st*sd;
st = st*cd + one*sd;
end
ratio = 6371.2/r;
rr = ratio*ratio;
p=NaN*ones(1,kmx);
q=NaN*ones(1,kmx);
% computation of Schmidt quasi-normal coefficients p and x(=q)
p(1) = 1.0;
p(3) = st;
q(1) = 0.0;
q(3) = ct;
for k=2:kmx
if n<m
m = 0;
n = n + 1;
rr = rr*ratio;
fn = n;
gn = n - 1;
end
fm = m;
if m==n && k~=3
one = sqrt(1.0 - 0.5/fm);
j = k - n - 1;
p(k) = one*st*p(j);
q(k) = one*(st*q(j) + ct*p(j));
cl(m) = cl(m-1)*cl(1) - sl(m-1)*sl(1);
sl(m) = sl(m-1)*cl(1) + cl(m-1)*sl(1);
end
if m~=n && k~=3
gmm = m*m;
one = sqrt(fn*fn - gmm);
two = sqrt(gn*gn - gmm)/one;
three = (fn + gn)/one;
i = k - n;
j = i - n + 1;
p(k) = three*ct*p(i) - two*p(j);
q(k) = three*(ct*q(i) - st*p(i)) - two*q(j);
end
%Synthesis of x, y, and z
lm = ll + l;
one = (tc*gh(lm) + t*gh(lm+nc))*rr;
%DEBUG
%[nyear,ncoef]=decode_coeff_pointer(lm);
%fprintf('nyear %6i %5i %5i \n',lm,nyear,ncoef);
if m~=0
two = (tc*gh(lm+1) + t*gh(lm+nc+1))*rr;
three = one*cl(m) + two*sl(m);
x = x + three*q(k);
z = z - (fn + 1.0)*three*p(k);
if st~=0
y = y + (one*sl(m) - two*cl(m))*fm*p(k)/st;
else
y = y + (one*sl(m) - two*cl(m))*q(k)*ct;
end
l = l + 2;
else
x = x + one*q(k);
z = z - (fn + 1.0)*one*p(k);
l = l + 1;
end
m = m + 1;
end %k loop
% conversion to coordinate system specified by itype
one = x;
x = x*cd + z*sd;
z = z*cd - one*sd;
B =[x; y; z];
%f = sqrt(x*x + y*y + z*z);
return
**********************************************************
function [gh,date]=GetIGRF11_Coefficients(varargin)
%Get IGRF11 Coefficients from Excel file
OutputMATfile=[];
if ~isempty(varargin)
OutputMATfile=varargin{1};
end
ff='igrf11coeffs.xls';
if exist(ff,'file')~=2
ff=pickfile('*.xls','Get igrf11 coefficients');
end
num = xlsread(ff);
num=num';
dd=num(3:end,1);
ndate=length(dd);
date=cell(1,ndate);
for n=1:ndate-1
date{n}=num2str(dd(n));
end
date{ndate}='2010-15';
num=num(3:end,2:end);
gh = NaN(1,3255);
for n=1:19
n1=(n-1)*120+1; n2=n*120;
gh(n1:n2)=num(n,1:120);
end
for n=20:24
n11=n2+(n-20)*195+1; n22=n2+(n-19)*195;
gh(n11:n22)=num(n,1:195);
end
if ~isempty(OutputMATfile)
save GHcoefficients gh
end
return
***************** Fin de la page *****************
Achevé juin 2014