EVOLUTION 

DES PARAMETRES ORBITAUX

Cette page est consacrée aux effets des perturbations sur les paramètres orbitaux et la position d'un nanosatellite expérimental. 

Rappelons la dénomination des paramètres orbitaux : a demi-grand axe, e excentricité, i inclinaison orbitale, W longitude du nœud ascendant, w argument nodal du périgée, to instant d'injection par exemple. Nous ne conservons que les effets séculaires ( long terme moyenné ) et laissons le soin au lecteur de retrouver les résultats.

I DONNEES SATELLITE :

Orbite initiale:  quasi circulaire, héliosynchrone à 817 km ( a=7195 km ),excentricité e=0.001165, inclinaison initiale i=98°.702, argument nodal du périgée w=90°, anomalie moyenne=270°.133336, longitude du nœud ascendant W = 62°.4731 +0.98564735*N où Nest le nombre de jours juliens depuis le 1 janvier 2000, Heure locale au nœud ascendant H = 21 h 30

Remarque : Pour une excentricité de 1.165 10^-3 on considère l'orbite comme circulaire. ( la différence a-b = 5 m !!! )

La masse est prévue de l'ordre de 3 kg maximum, la surface frontale S= 2 dm²

II PERTURBATIONS EN JEU :

Rappelons les succinctement en comparant l'accélération a en m/s²:

- Gravitationnelles et conservatives ( pas de pertes d'énergie ) :

-  de la Terre J2  ( a = 10^-2 m/s² )    J4 ( a = 10^-5 m/s² )  J6 ( a = 10^-6 m/s² ). Essentiellement J2 agit sur W et w mais pas sur a, e, i.

-  Lune et soleil   ( a = 10^-6 m/s², 10^-8 m/s² ), les ouvrages spécialisés indiquent qu'il n'y a pas d'effet séculaire notable sur les paramètres orbitaux, seules des variations à longue période peuvent apparaître. Pour notre cas, nous oublions ces perturbations.

- Planètes   ( a = 10^-10 m/s² ) que nous oublierons bien évidemment

- Le frottement atmosphérique ( a = 10^-7 à  10^-8  m/s² ), force dissipative, son effet est négligeable sur i et porte essentiellement sur a et e. Comme le frottement a tendance à circulariser l'orbite et que e est voisine de 0 au départ, nous ne garderons que l'effet principal sur la vitesse et donc a. Par contre si a varie, il y a un effet secondaire sur W et w.

- La pression de radiation, constante en repère inertiel ( a = 10^-7 m/s² ), si le satellite " voit " le Soleil sinon nulle, force dissipative ou pas.

- Les marées ( a = 10^-6 à  10^-7  m/s² ) 

- L'albédo terrestre  ( a = 10^-8 m/s² )

 - Les effets relativistes que nous négligerons, mais pris en compte pour d'autres applications comme le GPS. Ils provoquent une dérive du périhélie de quelques minutes d'arc par an. Sans importance pour nous.

III EVOLUTION DU GRAND AXE :

1°) Effet de la traînée :

La traînée par kg en orbite se calcule par 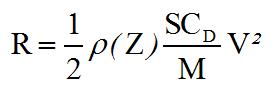Le coefficient de forme est SCd/M

Nous sommes sur une orbite héliosynchrone, très proche de celle de Spot, or Spot avait une masse M=2800 kg, une surface S=12 m² et un coefficient' aérodynamique Cd = 2,7.

Si on garde le même Cd, on a pour Spot S/M = 12/2800 = 0,0043 et pour le nanosatellite S/M = 0,02/3=0,00666, le rapport nano /Spot est de 1,55. Donc R_nano = 1,55 R_spot

Partons de l'équation de l'énergie et du théorème de l'EC

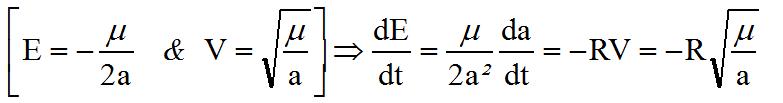
Donnant littéralement puis numériquement :

Or, il était bien connu ( source CNES ) que SPOT descendait de 2,5 m/jour, donc avec le facteur proportionnel 1,55 on a, pour notre nanosatellite une descente de 4 m/jour ou 1,46 km/an

Quelle conséquence sur la position ?

En restant sur le cercle et en oubliant les autres paramètres orbitaux, la vitesse évolue comme ci-dessous :

Ne soyons pas surpris, ce n'est qu'un paradoxe apparent, la traînée fait croître la vitesse, car simultanément elle freine, permettant au satellite de descendre donc de récupérer de l'énergie sur le potentiel. Au final le bilan est positif. Nous savons fort bien que plus un satellite est bas, plus il tourne vite.

Le décalage de la position sur l'orbite évolue donc de manière parabolique à partir du lancement :

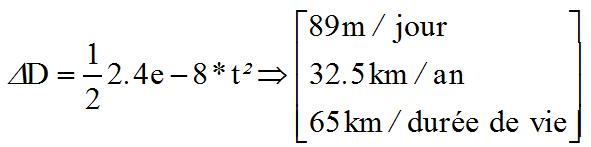
A 7,4 km/s, 65 km de distance donnent un écart de 8 à 9 secondes sur la position, ou encore un écart angulaire de 1°.5. Peut-être est-ce supportable si la régulation travaille à 3° près?.

Ceci fait l'objet d'une simulation, où on calcule le champ de consigne avec 9 s d'erreur, tout en gardant pour le calcul du couple magnétique la valeur du champ réel pulsé, compte tenu de la mesure. En pratique, le calculateur pourrait prendre en compte ce décalage et utiliser le modèle de champ magnétique pour estimer la " bonne valeur du champ ".

La simulation NANOLAUR/NANOSIM2.M permet de choisir avec dans l'ordre les données --> clic1 lance nanodat0.m + clic2 --> valeur de H + --> clic 3 valeur du retard deltaT. En sortie les courbes sont visualisées et le résumé peut-être obtenu dans l'espace Matlab

On trouve le tout dans NANOLAUR.ZIP

IV EFFETS SECULAIRES DES AUTRES PERTURBATIONS

Les perturbations d'origine gravitationnelles dérivent d'un potentiel, donnant lieu à des forces conservatives qui ne jouent en moyenne que sur W et w et n'affectent pas a et e.

1°) Effet de J2 :

- Aplatissement terrestre ( terme J2) qui ne joue pas sur a, e, i mais uniquement sur W et w.

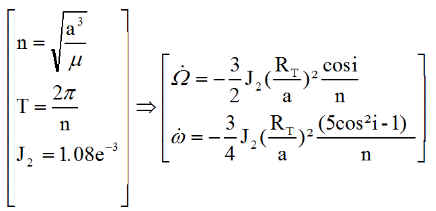
Avec donc comme valeurs initiales :

Bien évidemment, la première valeur correspond à une orbite héliosynchrone. La deuxième valeur affecte la position sur l'orbite.

2°) Attractions de la Lune et du Soleil :

Elles n'affectent pas a et e en variations séculaires:

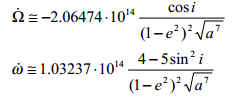
3°) Effet de la pression de radiation :

Cet effet est beaucoup plus difficile à évaluer et encore plus à calculer, car dépendant de l'activité solaire. 

Les radiations émises par le Soleil exercent sur les surfaces éclairées, une pression résultante estimée à p = 4.51 e-6 N/m². En pratique, suivant la nature de la surface éclairée ( miroir ...corps noir ) il faut affecter un coefficient de réflectivité ( 0 à 2 ) pour obtenir la force qui donne une accélération dans la direction du Soleil pour le coefficient 1 de:

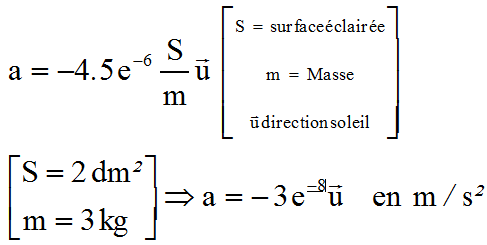
NB : Au-dessus de 800 km, cette force rivalise puis l'altitude augmentant, prend le dessus sur le frottement atmosphérique.  

Mais si l'on part de l'idée que l'ordre de grandeur est presque le même que celui du freinage atmosphérique et surtout que sa direction, contrairement à la traînée, est presque constante sur une orbite constamment éclairée, on peut espérer qu'en moyenne l'effet sera moindre du moins sur la position angulaire. Par contre le plan orbital y sera plus sensible.

VI RESULTATS DES SIMULATIONS nanosim2.m:

Le retard peut être choisi, 0, 5 , 10, 100 secondes. Pour 5 s les angles ne sont que peu affectés, pour 100 ils le sont beaucoup.

Roulis=0°,12366 tangage=4°,999 lacet = -2°,3276 durée=3131 s

au lieu de

Roulis=0°,957 tangage=4°,999 lacet = -2°,16366 durée=3167 s

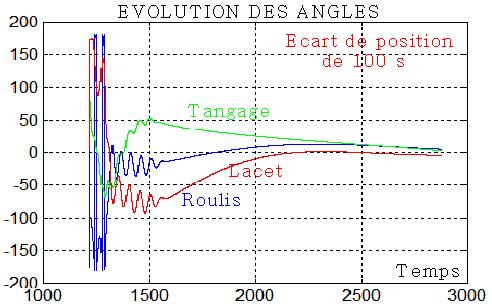
Roulis=4°,994 tangage=2°,618 lacet = -4°,0823 durée=2881 s

au lieu de

Roulis=0°,957 tangage=4°,999 lacet = -2°,16366 durée=3167 s

NB : Cette simulation m'amène à penser au test d'arrêt qui porte sur les angles et les vitesses angulaires, ce qui laisse supposer que je sais les mesurer. Mais est-ce le cas avec la régulation de Laurens utilisant un minimum de technologie?

 Donc, si je reste dans l'esprit de Philippe Laurens, la seule mesure que je sais faire c'est celle de Bc-B ou de sa dérivée. En effet B est mesuré à bord avec un magnétomètre 3 axes et Bc est donné par l'estimation de position permettant le calcul du champ IGRF du lieu.

 En pratique, il faut surveiller les deux. Pourquoi? Simplement parce que le hasard peut donner Bc-B nul alors que cette quantité évolue peut-être à grande vitesse, notamment durant le tumbling. Donc, il faut aussi surveiller la dérivée, ce qui revient à surveiller le couple de commande exercé sur le satellite.

Je vais donc essayer de cerner une borne supérieure au couple de commande. La simulation parfaite donne une valeur finale de 8 e-7 mN qui paraît acceptable, vue qu'elle est supérieure aux perturbations.

EXEMPLE DE RESUME DE NANOLAUR/NANOSIM2 ( H=0.0032 mNs et deltaT=100 )

*************** PRINCIPALES DONNEES DE LA SIMULATION ***************
Nanosatellite nanolaur/nanosim2.m initialisée par nanodat0.m
------------------------------------
***********************************************************************

Latitude d'injection = 70 °
Heure d'injection = 1213 s Avec rappel convention --> Heure =0 s au survol équateur
Heure de fin de Tumbling = 1248 s, soit 34.84 s, après l'injection

--------------------- RESPECT DES SPECIFICATIONS ------------------------
Moment magnétique maximum bobine = 0.2 Am²
Vitesse angulaire de coupure en fin d'acquisition detumbling = 0.002 rd/s
Ecart maximum de pointage en acquisition fine = 5 ° 
Ecart angulaire maximum toléré sur le quaternion = 10 ° 
Couple maximum sur la roue = 4e-006 Nm
Nombre minimum de points stockés pour les courbes = 4e+004

Consigne de tangage = 0 rd
Consigne de roulis = 0 rd
Consigne de lacet = 0 rd

Simulation avec champ pulsé

Période des mesures = 5 s
Durée de la mesure = 0.1 s
Retard orbital deltaT = 100 s 

--------------------- COEFFICIENTS DE LA REGULATION ------------------------
La simulation comporte 2 couples en parallèle, avant calcul des moments magnétiques
Action 1 : régulation de type PD de Laurens avec champ magnétique de consigne
KPD_laurens= 0.000016 SI, pour le rappel proportionnel
FPD_laurens= 0.0084 SI, pour l'amortissement sur la dérivée

Action 2 :régulation de type PD sur l'angle de rotation du quaternion
KRG= 0.24 SI, pour le rappel proportionnel à l'angle de rotation
KFG= 0.14 SI, pour l'amortissement sur la dérivée de l'angle de rotation
gain_pour_essai= pour les essais

NB : Les coefficients peuvent etre modifiés dans le module dédié de la simulation
ou directement dans l'espace Matlab

--------------------- VALEURS INITIALES ------------------------
Angle de roulis = 1.3 rd Vitesse de roulis = 0.06 rd/s
Angle de tangage = 1.4 rd Vitesse de tangage = 0.05 rd/s
Angle de lacet = 0.05 rd Vitesse de lacet = 0.01 rd/s

--------------------- FONCTIONNEMENT DE LA ROUE ------------------------
Inertie de la roue J_ROUE= 0.000032 m²kg 
Vitesse initiale = 100 rd/s ou 954.9 tours/s
Vitesse finale = 100 rd/s ou 954.9 tours/mn
Rotation maximale = 360 rd/s ou 954.9 tours/s
Moment cinétique H = 0.0032 mN/s 
--------------------- RAPPEL DES CONDITIONS INITIALES ------------------------
Vecteur à 7 composantes initialisant l'intégration par le quaternion d'attitude en repère orbital

etat_init = [0.06986 0.01534 -0.04871 0.6184 0.4499 0.5243 -0.3745]

Rotation absolue initiale en repère satellite: p=u(1) q=u(2) r=u(3)
Quaternion d'attitude initiale par rapport au repère orbital:Q =[u(4) u(5) u(6) u(7)]

********************************* FIN DES SORTIES ***********************************
Le Stop de la simulation est commandé par 3 conditions simultanées ( fonction AND ) :
1 - Racine carrée de la somme des carrés des angles < à un minimum fixé plus haut
2 - Angle de rotation du quaternion < à une valeur précisée plus haut
3 - Vitesses angulaires inférieures à un seuil prédéterminé

**************     Ces seuils peuvent être supprimés ou adaptés suivant la mission       ****************

****************************** Fin de page ********************************