EXEMPLE DE RESTITUTION D'ATTITUDE
SUR UN NANOSATELLITE
I QU'EST-CE QUE LA RESTITUTION D'ATTITUDE D'UN SATELLITE ?
La restitution d'attitude consiste à l'aide de capteurs à calculer à chaque instant, au plus juste, l'orientation de 3 axes privilégiés du satellite, dans un repère de référence connu, qui peut être inertiel ou lié au mouvement orbital.
Cette restitution doit permettre, dans notre cas, de calculer, indifféremment :
- La matrice de passage de Ro à R
- Les angles d'orientation ( Euler ou Cardan ) du repère R par rapport à Ro
- Le quaternion d'attitude Q qui caractérise la rotation faisant passer de Ro à R
Vous trouverez sur Internet une multitude d'articles consacrés à cette question et une grande variété de réponses dépendant du satellite, de sa mission, circumterrestre ou interplanétaire, des équipements emportés :
II CAS D'UN NANOSATELLITE
En ce qui me concerne, je résume le problème, très simplement pour le cas d'un nanosatellite à bas coût, disposant d'un équipement minimal au départ. Le repère de référence est le repère orbital classique noté Ro ( X Y Z ), le repère satellite est R ( x y z ).
Comme le SCAO repose essentiellement sur l'utilisation du champ magnétique terrestre, de 3 magnétocoupleurs et d'une roue, nous restons dans cette optique et commençons par envisager d'emporter à bord:
- un magnétomètre 3 axes, fournissant les composantes du champ magnétique local dans les axes satellite, repère R = ( x y z ) donc ( Bx By Bz ) est la mesure du champ.
- un modèle de champ magnétique ( par exemple IGRF ) permettant de connaître le champ magnétique local, dans Ro ( X Y Z ) , les compoqantes sont BX BY BZ, avec comme seule contrainte de connaître la position orbitale ou une estimée de la position avec la date et une position antérieure correcte ou les paramètres orbitaux.
NB : Pour un équipement minimum, il suffit d'emporter 2 magnétomètres et le modèle de champ magnétique. En effet, avec 2 composantes et le module du champ donné par donné par le modèle, on en tire la troisième composante au signe près. En pratique, le magnétomètre supplémentaire assure la la sécurité du système.
1°) PEUT-ON RETROUVER L'ATTITUDE D'UN SATELLITE AVEC UNE MESURE MAGNETOMETRIQUE?
En clair, peut-on retrouver la matrice de passage P d'un repère Ro à un repère R, avec la seule connaissance des composantes d'un vecteur Vo et de son image V, dans chacun de ces repères. Pour nous le vecteur V sera associé au champ magnétique terrestre.
La réponse est non, bien que l'on soit très près de la solution. En effet :
Soit P la matrice cherchée, qui est dans tous les cas une matrice de rotation ( rotation d'axe u et angle q ) alors si Q est la matrice d'une rotation ( axe unitaire de B, angle d ), faisant passer de R à R1, les composantes de B dans R et R1 restent les mêmes.
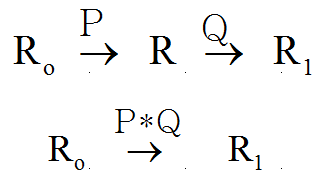
Ce qui signifie que
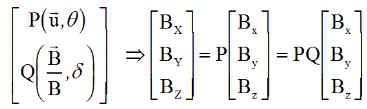
Pour conclure, l'attitude ne peut être connue qu'à une rotation près quelconque autour de l'axe de la direction de B. Autant dire qu'il n'y a plus qu'une seule inconnue, l'angle d de la rotation.
2°) QUE FAUT-IL RAJOUTER?
Pour lever l'ambiguïté, il suffit d'avoir une autre référence de direction, par exemple la direction Terre-Soleil, par exemple grâce à un senseur solaire. On pourra donc calculer d et donc complètement préciser la matrice P et l'attitude du satellite.
NB : la référence supplémentaire peut provenir de tout type de capteur.
III CHAÎNE DES CALCULS :
N'ayant pu trouver sur Internet aucun article à ce sujet ( Si vous en trouvez donnez-moi les adresses ), je me suis lancé dans une logique toute personnelle.
1°) Préparation des calculs :
On connaît à bord :
a) Le vecteur champ magnétique B terrestre local, exprimé en repère satellite. On note b son unitaire, ce qui nous débarrasse de la norme.
b) Une direction Satellite - Soleil ( ou autre ) notée S, dont s est l'unitaire.
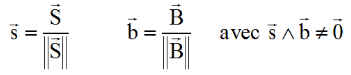
J'introduis un repère intermédiaire qui semble adapté au problème. Appelé R1, il comprend dans l'ordre s, t, w 3 vecteurs unitaires intimement associés au problème. Le second t est aussi le produit vectoriel de w par s.
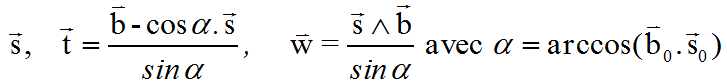
a ( de 0° à 180° ) est l'angle de repérage de b, dans le plan ( s , t )
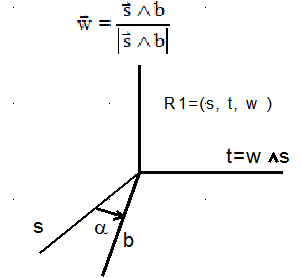
2°) Données connues du calculateur :
Dans la suite, on introduit avec l'indice 0, les vecteurs Bo, So, bo, so considérés comme connus dans Ro, mais entachés d'erreurs
| Repère orbital R0 XYZ | Repère satellite R xyz | Repère R1 s t w | |
| Champ magnétique local
B et son unitaire b |

(Modèle IGRF par exmple ) |
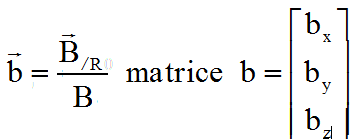
( Résulte de la mesure des magnétomètres ) |
 |
| Unitaire de la direction
S Terre soleil |
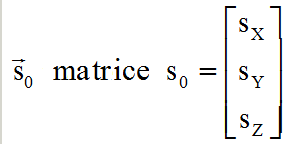
( Nécessite la connaissance de la position orbitale ) |

( Résulte de la mesure du senseur solaire ) |
 |
NB : On retiendra que la logique qui suit, suppose :
- Un modèle embarqué de champ magnétique terrestre
- La connaissance la plus précise possible de la position et de l'orbite du satellite et naturellement de la date
a) pour le champ magnétique IGRF et le repère Ro ( calcul de Bo )
b) Pour le repère Ro dans lequel, la donnée de la date permet de retrouver l'unitaire Terre-Soleil ( So )
Matrice W=PQ de passage R0 à R1 :
Cette matrice est facilement calculable puisque s et b connus dans R0, permettent le calcul de s t w, W est constituée, en colonnes, des 3 vecteurs qu'il suffit d'exprimer dans la base de Ro
Matrice de passage Q de R à R1 :
Aussi facilement calculable puisque b et s connus dans R permettent le calcul de s t w dans R donc la matrice Q est constituée, en colonnes, des 3 vecteurs s t w qu'il suffit d'exprimer dans la base de R
Matrice de passage P de Ro à R :
Avec les matrices W = PQ et Q, nous en tirons très aisément P, puisque Q-1 = Transposé(Q)
![]()
Nb : Les calculs sont relativement simples et faciles vérifier sur Matlab, spécialiste du calcul matriciel.
Précision de la restitution :
Il est clair qu'elle dépend :
- De la précision des magnétomètres
- De la précision du senseur solaire
- Mais surtout de la localisation du satellite et de la connaissance de ses paramètres orbitaux.
Remarque : a priori, les erreurs du senseur solaire ne sont dues qu'au dispositif et pas à l'imprécision de la localisation satellite. Par exemple une erreur de 1500 km sur le satellite, ne donnera qu'une erreur de 10-5 radian sur la direction de S, vue la distance Terre-Soleil = 150 106 km.
Le diagramme de fonctionnement pourrait ressembler à ceci :
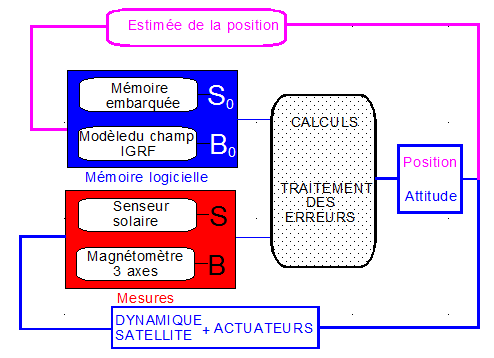
IV PROTOCOLE DE VERIFICATION SOUS MATLAB :
a) Calcul exact :
Je me donne les angles de Cardan roulis = F =30°, tangage = q = -50°, lacet = y = 120°, je calcule P:
- les 2 directions unitaires bo de B et so de S, dans Ro
- Une matrice P de passage, au hasard
- Je calcule b et s transformés de bo et so, par s = inv(P)*so' et b = inv(P)*b0'
Avec ces 4 données b, s bo, so je dois retrouver la matrice P et les angles de Cardan. Dans ce cas là ce sera parfait, puisqu'il n'y a pas d'erreurs introduites au départ.
Fonction Matlab utilisée --> Pcalcul = restitut(b0,s0,b,s); retrouver le programme
b) Détail des calculs :
- Calcul de la matrice de passage P :
u=[30 120 -50]*pi/180;P=P_card(u)

u=[30 -50 120]*pi/180; P=P_card(u) avec une fonction adaptée.
P =[-0.3214 -0.5585 0.7647
0.5567 -0.7647 -0.3245
0.7660 0.3214 0.5567]
- Calcul de b avecb0 donné :
b0 = [0.7803 0.0390 0.6242]; b = inv(P)*b0 = [ 0.2491 -0.2650 0.9315]'
- Calcul de s avec s0 donné aléatoirement
s0 = [ 0.7803 0.6242 0.0390 ];
s = inv(P)* [0.7803 0.6242 0.0390 ]' = [0.1266 -0.9006 0.4158]'
L'exécution dans Matlab de Pcalcul = restitut(b0,s0,b,s) redonne exactement la matrice P de départ ( Voir annexes )
NB : L'introduction d'une erreur de 5% sur les composantes de B et de S donne une erreur de moins de 2° sur les angles de Cardan
( programme testrest.m voir en annexe )
Retrouver tous les programmes utiles à cette page
************************************** FIN DE THEORIE ********************************
Magnétomètre 3 axes HM6352 https://www.sparkfun.com/datasheets/Sensors/MicroMag3%20Data%20Sheet.pdf
ANNEXES :
Pcalcul=restitut(b0,s0,b,s)
b0 =0.7803
0.0390
0.6242
s0 =0.7803
0.6242
0.0390
b =0.2491
-0.2650
0.9315
s =0.1266
-0.9006
0.4158
___________________________________________________
Pcalcul = -0.3214 -0.5585 0.7647
0.5567 -0.7647 -0.3245
0.7660 0.3214 0.5567
C'est bien la matrice de départ
********************** Programme 1 *******************
function Pcalcul=restitut(b0,s0,b,s);
b0,s0,b,s,
% b0 est l'unitaire du champ magnétique du modèle IGRF, calculé pour la position estimée, dans les axes XYZ de R0, le repère orbital
% b est l'unitaire du champ magnétique mesuré dans R = xyz de R, chmp manétique local réel
% s0 est l'unitaire dans les axes XYZ de R0, le repère orbital, de la direction Terre-Soleil estimée pour la date actuelle et la position estimée
% b est l'unitaire mesuré dans R = xyz le repère satellite, de la direction Terre-Soleil réelle
% Calcul de la matrice W de passage R0 à R1
W(1:3,1)=s0; % Vecteur colonne ou colonne 1 de s sur XYZ
u(1:3)=s0;
u(4:6)=b0;
unit_W=prodvect(u)/norm(prodvect(u)); % Produit vectoriel s0, b0 normalisé donnant w, vecteur colonne
W(1:3,3)=unit_W; % Colonne 3 w unitaire du produit vectoriel s0 par b0
u(1:3)=unit_W;
u(4:6)=s0;
W(1:3,2)=prodvect(u); % Colonne 2 t produit vectoriel w,s0 normalisé donnant w
% Calcul de la matrice X de passage R à R1
X(1:3,1)=s; % Colonne 1 de la matrice X
u(1:3)=s;
u(4:6)=b;
unit_WW=prodvect(u)/norm(prodvect(u)); % Vecteur w du repère stw
X(1:3,3)=unit_WW; % Colonne 3 de la matrice X
u(1:3)=unit_WW;
u(4:6)=s;
X(1:3,2)=prodvect(u); % Colonne 2 Produit vectoriel w, s normalisé donnant w
% Calcul de la matrice P de passage R0 à R
Pcalcul=W*inv(X);
end
********************** Programme 2 *******************
programme
testrest.m
clear
u=[30 -50 120]*pi/180;
disp(' Angles en degrés au départ, donc à retrouver ');
phi_deb=30,
teta_deb=-50,
psi_deb=120,
P=P_card(u);
disp(' Matrice P au départ, donc à retrouver ');P,
%P = [ -0.3214 -0.5585 0.7647
% 0.5567 -0.7647 -0.3245
% 0.7660 0.3214 0.5567)
% Introduction des erreurs
% Données de b0 et s0 estimées à 5% près
b0 = [0.7803*1.05 0.0390*0.95 0.6242]';
b0=b0/norm(b0); % A 5% près
% b=inv(P)*b0;
b =[ 0.2491*1.01 -0.2650*1.1 0.9315*0.99]'; % A 1% près
s0 = [ 0.7803*1.05 0.6242 0.0390*0.95 ]';
s0=s0/norm(s0);
s=inv(P)* [0.7803 0.6242 0.0390 ]'; % s= [0.1266 -0.9006 0.4158]'
% b0 est l'unitaire du champ magnétique du modèle IGRF, calculé pour la position estimée, dans les axes XYZ de R0, le repère orbital
% b est l'unitaire du champ magnétique mesuré dans R = xyz de R, chmp manétique local réel
% s0 est l'unitaire dans les axes XYZ de R0, le repère orbital, de la direction Terre-Soleil estimée pour la date actuelle et la position estimée
% b est l'unitaire mesuré dans R = xyz le repère satellite, de la direction Terre-Soleil réelle
% Récupération des entrées
% Calcul de la matrice W de passage R0 à R1
W(1:3,1)=s0; % Vecteur colonne ou colonne 1 de s sur XYZ
u(1:3)=s0;
u(4:6)=b0;
unit_W=prodvect(u)/norm(prodvect(u)); % Produit vectoriel s0, b0 normalisé donnant w, vecteur colonne
W(1:3,3)=unit_W; % Colonne 3 w unitaire du produit vectoriel s0 par b0
u(1:3)=unit_W;
u(4:6)=s0;
W(1:3,2)=prodvect(u); % Colonne 2 t produit vectoriel w,s0 normalisé donnant w
% Calcul de la matrice X de passage R à R1
X(1:3,1)=s; % Colonne 1 de la matrice X
u(1:3)=s;
u(4:6)=b;
unit_WW=prodvect(u)/norm(prodvect(u)); % Vecteur w du repère stw
X(1:3,3)=unit_WW; % Colonne 3 de la matrice X
u(1:3)=unit_WW;
u(4:6)=s;
X(1:3,2)=prodvect(u); % Colonne 2 Produit vectoriel w, s normalisé donnant w
% Calcul de la matrice P de passage R0 à R
% Matrice P recalculée
disp(' Matrice P en restitutiont,à comparer à P ');
Pcalcul=W*inv(X),
disp(' Angles en degrés en restitution, donc à retrouver ');
psi_fin=atan2(Pcalcul(2,1),Pcalcul(1,1))*180/pi,
phi_fin=atan2(Pcalcul(3,2),Pcalcul(3,3))*180/pi,
teta_fin=asin(Pcalcul(3,1))*180/pi,
y=W*inv(X);
end
______________________________ Fin de page ____________________________________