|
REDUCTION DU "TUMBLING" INITIAL D'UN SATELLITE PAR LA COMMANDE DE STEYN |
![]()
|
Retour index général |
Rédigé novembre 2015 Optimisation de l'énergie avec les magnétocoupleurs Saturation des magnétocoupleurs III STABILISATION ET MISE EN SPIN Moments de commande Stabilisation Y-Thomson V UTILISATION DE LA ROUE : Premiers choix non retenus VI SIMULATION COMPLETE AVANT REGULATION FINE : Résultats Lois de la commande fine Résultats sur 40000 secondes ANNEXES A -- Données de la mission
|
|
Contacts |
|
|
index nanosatellite |
![]()
On trouvera en annexe A les caractéristiques de la mission du nanosatellite étudié.
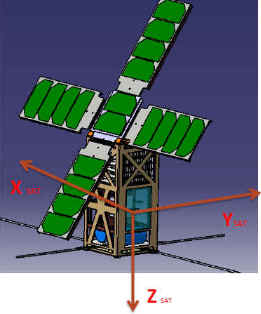
M'intéressant à la stabilisation et au pointage nadir d'un nanosatellite, il m'a été donné l'occasion de lire des publications au format pdf, de WH Steyn, Y Hashida et V Lappas concernant le contrôle d'attitude des nanosatellites SNAP-1 et ZA-AeroSat que le lecteur pourra retrouver en de nombreuses publications dont Adresse 1 Adresse 2 Adresse 3 Adresse 4.
Mon but est ici simplement d'essayer de comprendre cette commande, de transmettre éventuellement ma compréhension et les explications qui en découlent, à un lecteur intéressé et de vérifier par des simulations qu'effectivement cette commande est intéressante, ce qui ne fait bien sûr aucun doute.
Le SCAO d'un nanosatellite satellite doit être réalisé par le plus simple des systèmes : une roue située sur l'axe tangage et trois magnétocoupleurs. Pour l'instant, on ne s'occupe pas de l'électronique de traitement de l'information et des mesures dont les résultats alimentent la commande SCAO.
1°) Optimisation de la consommation électrique, valable pour toutes les simulations, avec magnétocoupleurs
Un magnétocoupleur fournit un couple grâce à son moment magnétique M, généré par un courant adéquat circulant dans la bobine. Il donne un couple de commande C.
![]()
Comme seule la composante du moment magnétique orthogonale au champ magnétique est efficace, nous optimisons la valeur de M en ne gardant que la composante Mopt normale au champ B
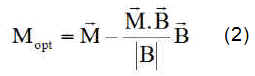
2°) Saturation des magnétocoupleurs
De plus, une spécification technique impose que la saturation des magnétocoupleurs doit être respectée, le maximum toléré ( pour l'exemple qui sera traité ) est Mmax = 0.2 Am² :
Ainsi, si 2 ou 3 magnétocoupleurs fonctionnent en parallèle, avec dépendance des uns par rapport aux autres, c'est le cas quand il n'y a qu'une seule loi de commande affectant les 3 axes, pour produire un moment dont la direction particulière est importante. On remplace alors le moment magnétique M par un autre réduit mais colinéaire Ms, ce qui conserve la direction.
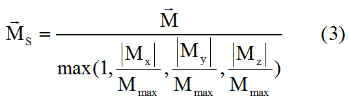
Soit individuellement, quand les commandes sur les axes sont indépendantes, à ce moment là, il suffit de brider le moment à 0.2 Am².
En simulation, la fonction magn_sat.m assure ce traitement.
II REDUCTION DES VITESSES ANGULAIRES ( DETUMBLING) :
1°) Qu'est-ce que le "tumbling"?
Lorsqu'un nanosatellite est lancé en orbite, l'éjection mécanique n'est jamais parfaite et le satellite part dans une rotation plus ou moins importante et surtout totalement aléatoire. Ce qui signifie que son vecteur rotation instantanée est strictement inconnu.
Comme la communication de Steyn le dit, une rotation de 5°/s est un ordre de grandeur classique, mais il arrive que 30°/s soient atteints juste après la mise en orbite.
2°) Ce qui est attendu d'un contrôle d'attitude ( S C A = Système de Contrôle d'Attitude )
Le nanosatellite étudié est placé en orbite héliosynchrone ( donc quasi orbite polaire ), la première étape après injection consiste en une stabilisation de l'attitude, avec l'axe de tangage normal au plan orbital avec une rotation autour de cet axe à une valeur prédéterminée qui le stabilise gyroscopiquement , de manière à pouvoir le reprendre dans une configuration connue.
Voir en annexe B les axes et les repérages angulaires
Une première étape est donc que l'axe satellite y reste aligné avec l'axe Y du repère orbital. C'est ce qui est appelé une "Y-Thomson attitude". Auquel cas, la seule rotation possible reste une rotation autour de y. La stabilisation complète n'est possible que si la rotation satellite est identique à la rotation orbitale wo ( pour nous 0.001 rd/s )
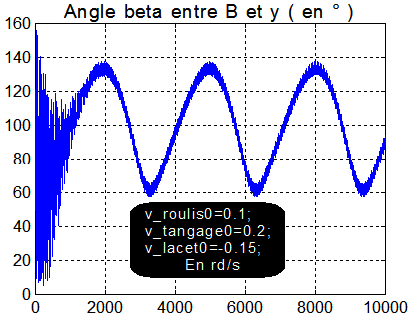
Comme la variation orbitale du champ magnétique est lente, la vitesse de l'extrémité du vecteur champ magnétique vue dans le repère satellite, révèle la rotation satellite parasite, autre que la rotation orbitale autour de Y ( très faible ). Le vecteur champ magnétique est quasiment dans le plan orbital, pour une orbite héliosynchrone, l'angle b est différent de 90° lorsque y et Y ne sont pas en quasi coïncidence. La rotation axiale autour de y ne modifie pas b, par contre une composante de la rotation transversale ( wT sur la figure ) normale à B et y fait varier b par l'intermédiaire de la vitesse VB de l'extrémité de B.
La figure suivante montre qu'un excellent moyen de détecter une rotation transverse est de suivre l'angle b.
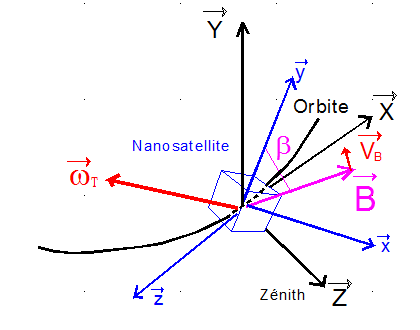
Steyn propose donc, une loi de commande avec un seul magnétocoupleur d'axe y : en effet
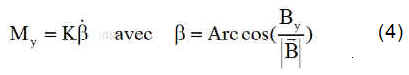
NB : Cette loi où l'on met en évidence la vitesse de l'extrémité du vecteur B fait partie de ce que l'on appelle les lois en "B-dot". Voir une autre loi en "B-point"
Vérification d'une puissance négative :
En effet, on a un couple de commande C qui vaut :
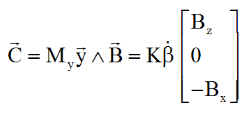
NB : En pratique, le champ magnétique évolue tout au long de l'orbite, mais le couple est toujours actif, soit au passage équateur avec la composante Bx maximale, soit au passage pôle avec Bz où cette composante est aussi maximale..
Sa puissance est :
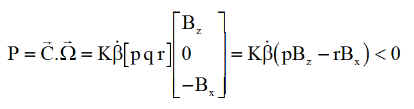
toujours négative comme le prouve le développement qui suit.
La dérivée d'un scalaire ne dépend pas du repère choisi pour exprimer les vecteurs. Donc prenons le repère satellite.
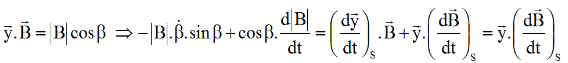
Or, la dérivée absolue du champ magnétique est très petite, tout comme la dérivée du module de B, ce qui entraîne, avec une excellente approximation ( celle adoptée dans toutes les régulations dites en Bdot )
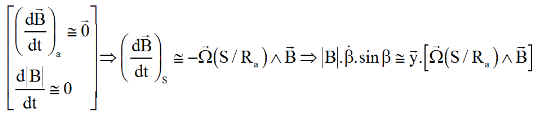
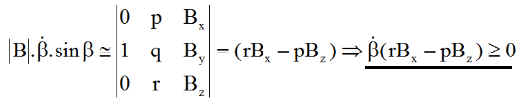
Montrant que la puissance du couple de commande est donc toujours négative et dissipative, ce qui est parfait en toutes circonstances pour réduire les vitesses angulaires transversales, comme toutes les commandes de type Bdot fondée sur la dérivée du champ magnétique.
Pour conclure, nous choisirons, la formule générale valable pour toutes les configurations, où K est un gain à choisir :
|
Avantages de cette commande: elle ne nécessite pas de connaître l'attitude du satellite par rapport aux axes orbitaux. Seuls les magnétomètres sont nécessaires
pour donner le champ magnétique B en axes satellites (Bx By Bz ).
EXEMPLE : Avec des données différentes de celles de CASAA-SAT, SIMULATION 1: ( simulation C:/steyn_1/tumble_1.m initialisée par stn_dat1.m)
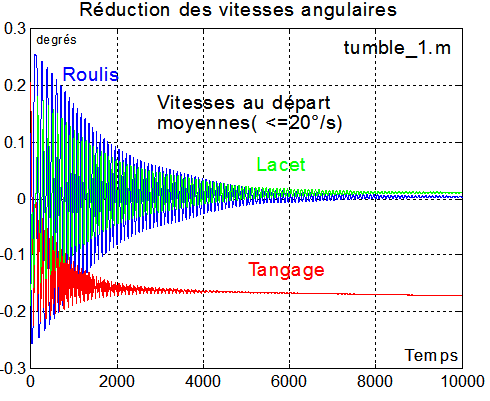
Les vitesses angulaires autres que le tangage sont réduites de manière très efficace et très élégante.
III REDUCTION DU DETUMBLING ET STABILISATION DE L'AXE y ( en parallèle ):

1°) Moments magnétiques de commande :
On adopte la commande la plus générale donnée par WH Steyn, Y Hashida et V Lappas ( voir Adresse 4 )
b) Commande de mise en spin autour de y:
On adopte la formulation de Steyn ....

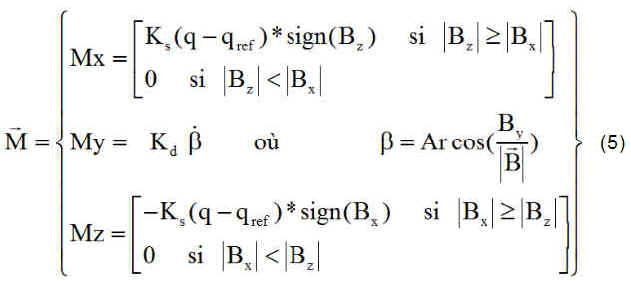
Calculons le couple magnétique C de composantes C1 C2 C3 et regardons de plus près ces composantes.
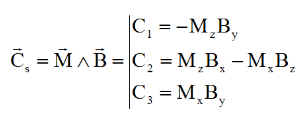
Le but à atteindre est de d'asservir la rotation de spin q à une valeur de référence qref. Il faut donc vérifier que sur l'axe y, la composante C2 est bien un rappel élastique, de signe contraire à l'écart q-qref . Le calcul qui suit montre qu'il en est bien ainsi, car la fonction y = x*signe(x) est toujours positive
| | Bz | > | Bx | | | Bx | < | Bz | | |
| Mx | Ks (q-qref)signe(Bz) | 0 |
| Mz | 0 | -Ks (q-qref)signe(Bx) |
| C2 = MzBx-MxBz | -Ks (q-qref)*Bz*signe(Bz) | -Ks (q-qref) *Bx*signe(Bx) |
|
Conclusion ( tous cas ) |
C2 = - Ks (q - qref) |
|
Voici 2 exemples avec C:/steyn_3/tumble_3.m initialisée par stn_dat3.m, de 2 mises en spin soit à à 5°/s après un "detumbling" sévère, soit à -3.2°/s suite à un "detumbling" à vitesses moyennes
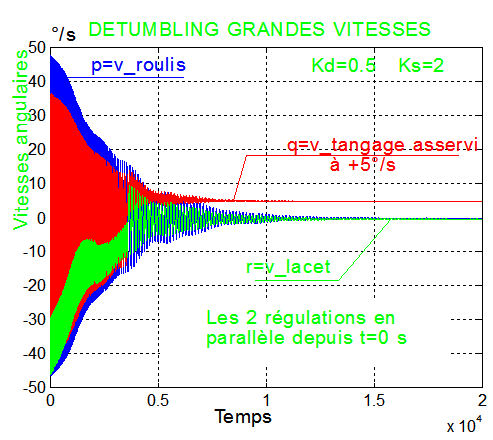
"Detumbling" sévère avec les 3 magnétocoupleurs en saturation durant 4000 secondes
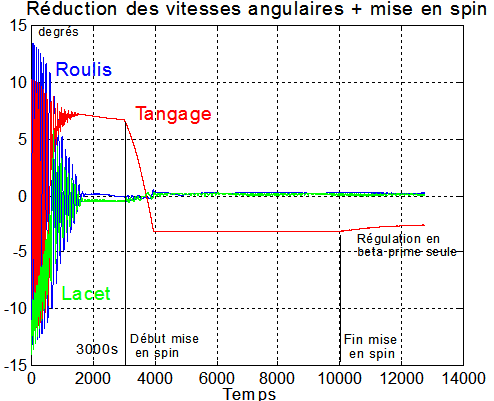
Exemple de mise en spin à -3.2°/s, début 3000 s arrêt 8000 s ( Kd=15 , Ks=5 SI )
c) Le mode de stabilisation Y_Thomson stabilisation :
C'est une stabilisation du satellite "spinné" autour de l'axe y, lui-même en quasi coïncidence avec la normale Y au plan orbital.
Il faut donc suivre l'angle ( noté angle_Y_y ) entre les unitaires y du satellite et Y du repère orbital. Si la matrice de changement de base est P, alors, moyennant l'argument compris entre -1 et 1: la fonction Ang_Y_y.m réalise ce calcul avec les précautions d'usage pour l'inversion des lignes trigonométriques.
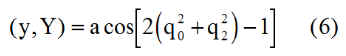
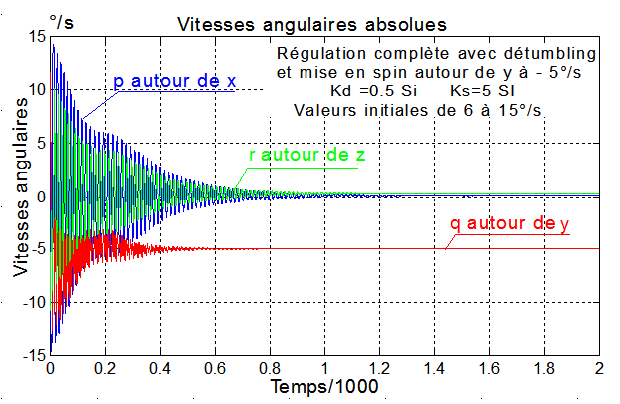
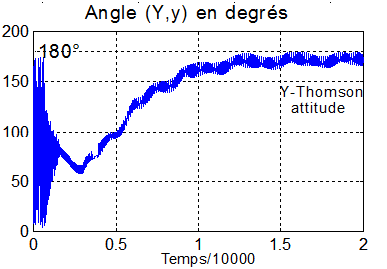
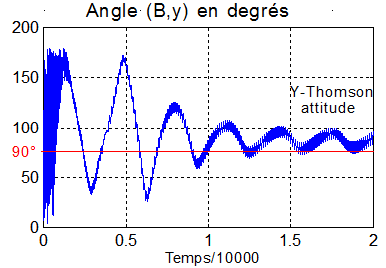
Deux courbes qui confirment l'alignement de l'axe de spin ( tangage y ) sur la normale Y au plan orbital
Mécaniquement parlant, le spin satellite s'aligne, par effet gyroscopique sur la rotation orbitale. Comme le spin est négatif, l'angle entre Y et y tend vers 180°, confirmé par l'angle entre B et y qui tend vers 90°( puisque B est pratiquement dans le plan orbital ).
IV ANNULATION DU SPIN SATELLITE ET STABILISATION DE L'AXE y:

Objet de la simulation C:/steyn_5/tumble_5.m initialisée par stn5dat.m
Physiquement, si on transfère intégralement le moment cinétique du satellite (qui servait, par effet gyroscopique, à aligner l'axe y sur la normale à l'orbite Y ), sur la roue, celle-ci va jouer le même rôle.
Comme la roue est à vitesse constante, les perturbations vont peu à peu dégrader la situation. En clair il va falloir aider la roue!!!
1°) Réduction et annulation de la vitesse angulaire q de tangage :
Cette commande d'après les indications des auteurs est réalisée par une roue, au départ au repos, puis mise en rotation autour de y, de manière à absorber la rotation q et à donner à la roue sa vitesse de travail autour de 600 tours/mn ( par exemple, c'était la proposition initiale ). Elle commence lorsque la configuration Y-Thomson est bien assurée.
Comme la manœuvre opère sur un satellite qui n'est pas de révolution, avec en plus les perturbations en action, une nutation peut apparaître que la régulation initiale avec un magnétocoupleur d'axe y, peut amortir.
J'ai fait le choix d'un couple progressif linéaire, donnant une évolution parabolique de la vitesse de la roue ( entre 0 et -600 tours/mn valeur de référence )
La commande complète est donc :
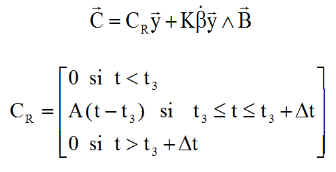
La constante A se calcule avec les conditions sur la vitesse de la roue ( Dt = 1000 s wref et Jroue= 2.2037e-5 m²kg ) ==> A = - 2.77e-9 Nm/s
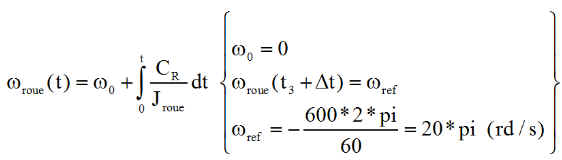
2°) Réflexions mécaniques :
Le moment cinétique principal ( sur y ) est totalement absorbé par la roue. Le satellite devrait ( sans les nutations parasites ) être fixe en pointage nadir. La roue joue le rôle de spin stabilisateur. C'est la configuration finale espérée
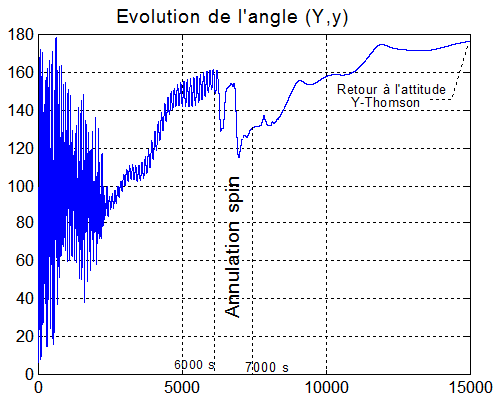
En pratique, les nutations en partie amorties par le magnétocoupleurs, vont peu à peu disparaître et le spin roue, par alignement sur la rotation orbitale ( 0.001 rd/s ), placera le satellite à nouveau en pointage nadir sans vitesses appréciables.
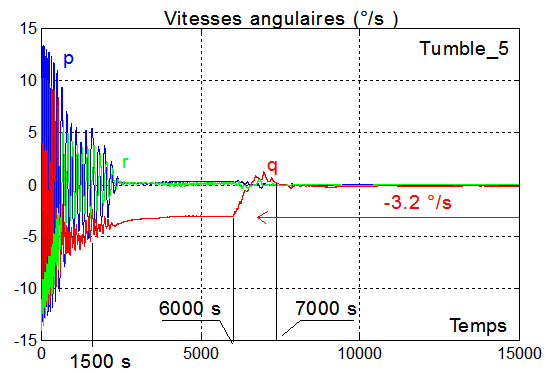
"Detumbling" de 0 à 15000 s+Mise en spin ( -3.2 °/s ) de 1500 à 6000 s+"despin" de 6000 à 7000 s
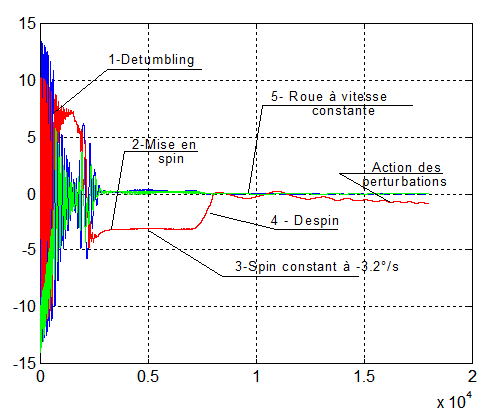
Le système différentiel reliant p q r et le quaternion d'attitude Q aux actions extérieures ou aux commandes, doit être adapté, en présence d'une roue, par la dérivée absolue du moment cinétique de la roue, au premier membre des équations donnant p q r :
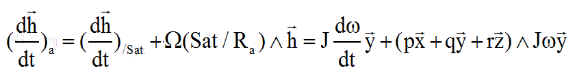
Ce qui donne avec l'opposé au second membre 2 termes de nature très différente (w est la vitesse angulaire de la roue et J son inertie axiale ):
- L'opposé du moment cinétique dérivé de la roue qui apparaît comme couple réactif de commande. Ou encore l'opposé du couple Cr agissant sur la roue
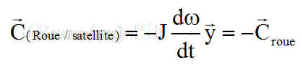
- Un couple perturbateur de couplage satellite/roue, créant une nutation parasite, mais sans consommation d'énergie, autant dire le couple n'amortit pas mais ne déstabilise pas non plus, il ne fait que partiellement contrarier la régulation, par le couplage.
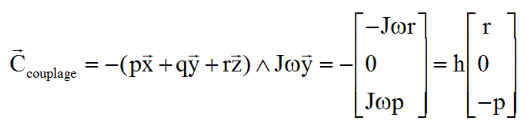
NB : On rappelle que comme tout couple de couplage gyroscopique, sa puissance est nulle, son effet n'est ni stabilisant ni déstabilisant mais consiste en un échange, à bilan constant, d'énergie entre les axes portant la nutation x ou z.
1°) PREMIERS CHOIX qui n'ont pas été retenus, mais instructifs :
La roue est caractérisée dans l'exemple choisi ( roue BCT )par :
- Un moment cinétique maximum hmax = 15 10-3 Nms
- Un couple maximum Cmax = 6 10-3 Nm
- Une vitesse de rotation maximale wmax = 6500 tours/mn
- Un moment d'inertie J = 2.2037 10-5 kg-m² autour de l'axe y
- Une vitesse de rotation choisie quasi constante autour de wref = -600 tours/mn
Il conduisaient à un choix de spin à -3.2°/s pour une roue à 600 tours/mn. En effet la roue doit "absorber " le moment cinétique du satellite créé après sa mise en spin à la vitesse qref.
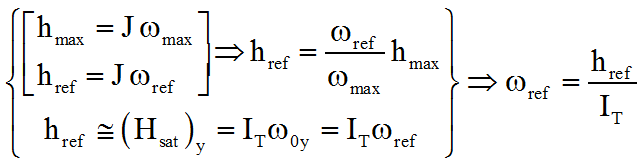
Le calcul donne pour la roue ci-dessus href = -1.38 10-3 Nms et qref = - 3.2 °/s .
2°) UTILISATION DE LA ROUE :
Une fois le "détumbling" et la mise en spin achevée, le satellite est normalement stabilisé en rotation à qref = - 3.2 °/s autour de l'axe y, normal au plan orbital, donc très proche de l'axe Y.
a) Réduction et annulation de la vitesse angulaire qref.
La roue est utilisée en boucle ouverte, signifiant que le moteur est commandé suivant une loi à choisir, sans rétroaction. En parallèle fonctionne le contrôle de b. Lorsque la vitesse angulaire qref est annulée, la roue doit être sensiblement à sa vitesse de travail, prévue à wref = - 600 tours/mn. En particulier, la loi du couple peut être constante ( cas plutôt théorique ) ou linéaire ce qui est plus naturel, ce qui devrait éviter un choc au lancement.
VI SIMULATION COMPLÈTE AVANT RÉGULATION FINE:
Cette simulation rassemble les 3 phases de régulation, avant la régulation du mode fin, assurant le pointage correct durant toute la mission.
C:/CASAA/TUMBLE00.M initialisée par STN5DAT.M
A partir de ce stade, nous adoptons les caractéristiques nouvelles de la roue adoptée définitivement : Jroue = 2.029210-6 kg m², qref = - 1 °/s wref = 2000 tours/mn
1°) Avec un tumbling initial à des vitesses angulaires moyennes après mise en orbite : Vitesses maximum de l'ordre de 15°/s.
Détumbling assuré par K_beta=15;K_stab=3; temps_phase1=25000;temps_phase2=3000;temps_phase3=8000;temps_stop=1000;
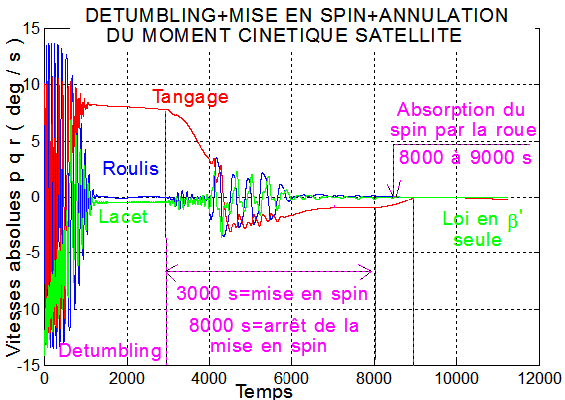
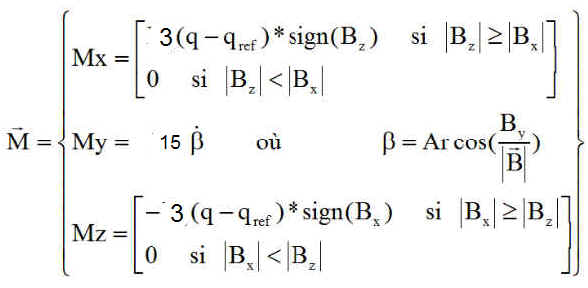
| wx | < 0.025°/s, | wy | < 0.3°/s, | wz | < 0.06 °/s
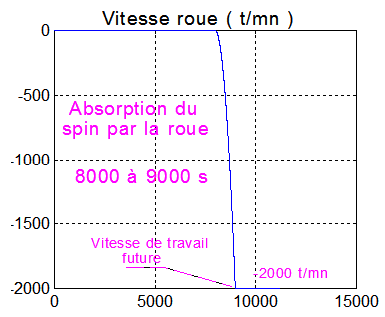
Vitesse roue amenée à -2000 tours/mn
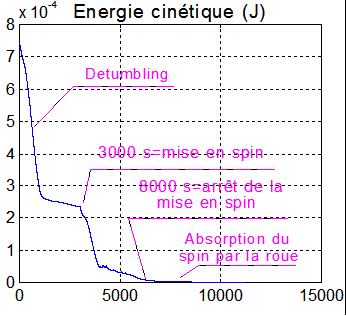
energie_zero=0.5*[vp0 vq0 vr0]*Asat*[vp0 vq0 vr0]'=7.43 10-4 J
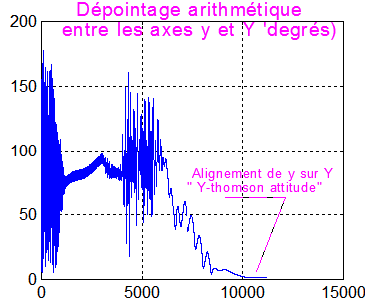
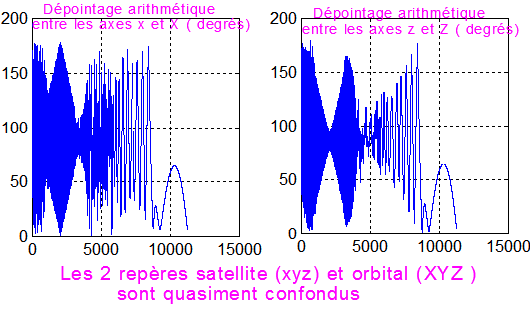
La mission se présente bien, il suffit maintenant de pérenniser la situation
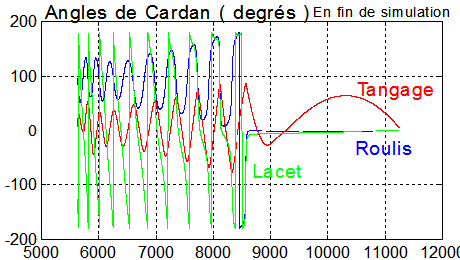
Confirmation de l'alignement (xyz) sur(XYZ). Le vecteur d'état est init_sca_fin = [0.0000 -0.0032 0.0000 -0.9990 0.0021 -0.0430 -0.0158], ce qui conforte les résultats car:
- Les 3 premières composantes sont les vitesses angulaires absolues, en rd/s, la plus forte est celle de tangage, sensiblement 0.0032 rd/s = 0.183 °/s, donc très faible.
- Les 4 dernières donnent le quaternion d'attitude, q1 = - 0.9999, sensiblement -1, confirme que le demi angle de rotation du quaternion est quasiment 180 ° et donc son double 360° ce qui donne xyz confondus pratiquement avec XYZ.
VII REGULATION FINE EN CONTRÔLE 3 AXES: analogue à celle de "SNAP-1 Nanosatellite"
C:/CASAA/SCA00FIN.M initialisée par STN00DAT.M
Elle reprend le vecteur d'état de la simulation précédente. Ce vecteur d'état final a été stocké dans InitFin.mat ( variable init_sca_fin )
Le satellite est maintenant quasiment sans vitesses angulaires, et donc assez près de son attitude de travail qu'il va falloir préciser puis maintenir par le contrôle 3 axes utilisant simultanément une roue et 3 magnétocoupleurs.
On appelle qref la valeur de consigne éventuelle de l'angle de tangage. Cet angle peut ne pas être nul, mais pour notre application, avec un pointage Nadir, il le sera. Simultanément, on souhaite garder la vitesse de la roue pratiquement constante ( moment cinétique h quasi constant et égal à href ).
Cette rotation, par le jeu du couplage gyroscopique, va générer une nutation parasite ( rotation transverse ), donc des vitesses angulaires parasites en roulis et tangage. Pour y parer les magnétocoupleurs sont sollicités avec un moment magnétique total M dont le calcul repose sur un double produit vectoriel, à partir du vecteur e, qui se calcule avec les vitesses angulaires wX et wY du satellite par rapport au repère orbital et non le repère absolu ni le satellite.
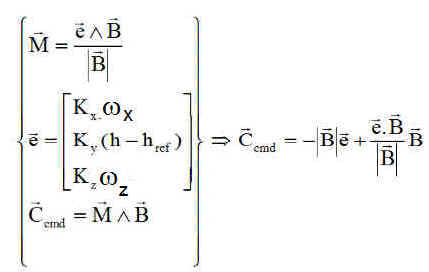
NB : On voit bien apparaître, sur les composantes 1 et 3, un rappel amortisseur des nutations transverses wx et wy, un couple de rappel sur l'axe y du satellite, grâce au coefficient |B|, induisant de manière indirecte un contrôle de la roue qui travaille donc à vitesse quasi constante.
Le fonctionnement de la roue à vitesse constante est en fait une désaturation de la roue en continu, évitant de programmer cette opération à intervalles réguliers.
NB : Dans un souci d'optimisation de la consommation électrique, il n'est pas nécessaire de supprimer comme à l'habitude ( voir ci-dessous ) la composante de M portée par B, car e est normal à B.
Calcul des vitesses angulaires par rapport au repère orbital XYZ
w0 est la mesure arithmétique de la vitesse de rotation orbitale ( 0.001 rd/s en valeur absolue)
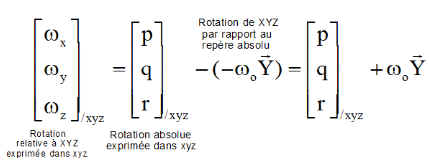
Ou encore, en utilisant le quaternion d'attitude Q ( de xyz / XYZ ) et la matrice de passage associée qui donne les composantes de Y ( P21 P22 P23 )sur xyz, on a :
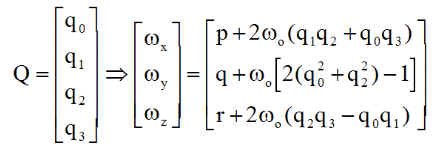
b) Résultats sur 40000 s : avec comme données de la régulation ( on notera que le couple de la roue sur le satellite est l'opposé du couple roue programmé )
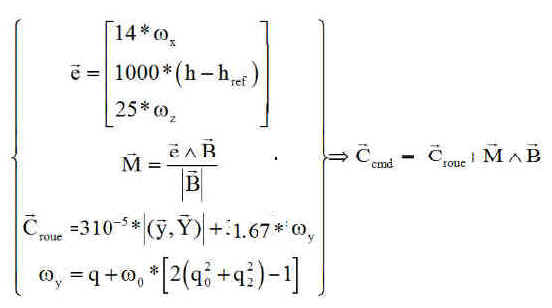
Remarque : le comportement de la roue est très sensible au gain du tangage sur le vecteur e, comme le montrent les 2 graphes sur la roue. Par contre les autres paramètres n'en sont pratiquement pas affectés.
Pour la roue, le couple de commande de la roue est C, la vitesse angulaire w. La logique de Steyn utilise l'angle q* entre z et Z, autant dire le dépointage de l'axe satellite par rapport au Nadir
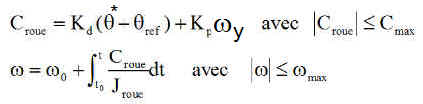
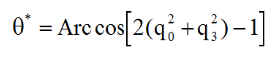
* Kx Ky Kz Kp Kd sont des gains constants, Jroue le moment d'inertie de la roue, wmax et Cmax vitesse et couple maximum admissibles pour la roue
* h = Jw est le moment cinétique instantané de la roue, w sa vitesse angulaire, wx et wy les vitesses angulaires relatives au repère orbital, de roulis et lacet
* h_ref est le moment cinétique de consigne de la roue ( censée travailler autour de sa vitesse de consigne de -2000 tours/mn ).
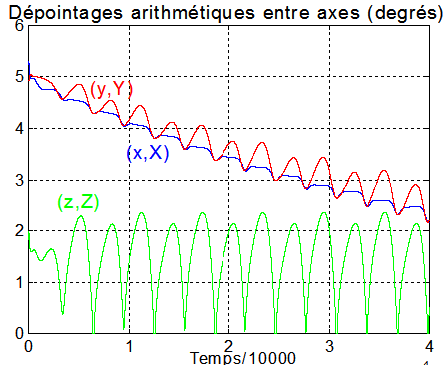
La spécification de pointage Nadir est largement satisfaite
Remarque : les résultats sont affectés d'une oscillation qui est bien connue pour toutes les régulations utilisant le champ magnétique terrestre? En effet la période est d'environ 3000 s soit la moitié de la période orbitale. Ceci, à cause du champ magnétique qui oscille, sur l'orbite de pulsation w0 à la pulsation 2w0.
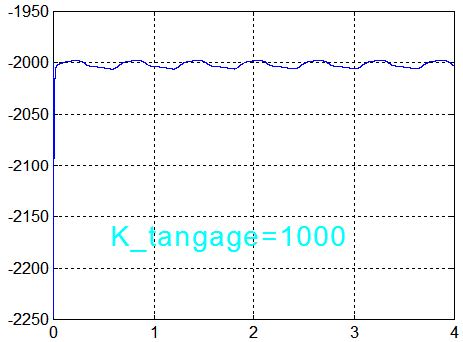
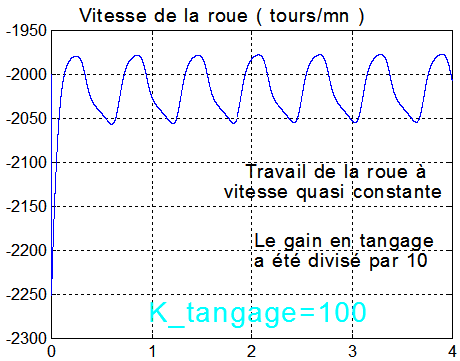
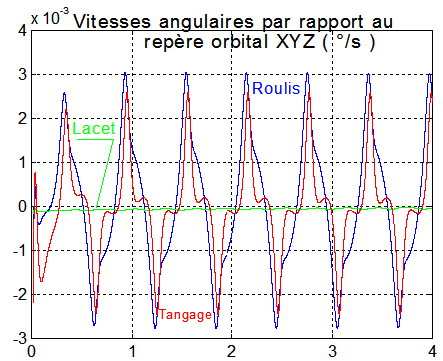
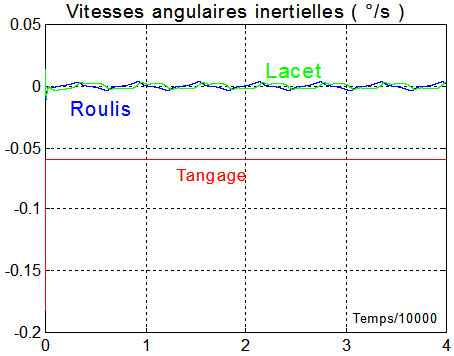
NB : la constance du tangage absolu à q(length(q)) = - 0.0593 °/s nous convient parfaitement, car elle confirme bien 2 points rassurants :
1- Que l'axe y est bien de sens contraire à la rotation orbitale, donc coïncide avec Y du repère orbital
2 - Que nous retrouvons la vitesse orbitale w0 = 0.0593*pi/180 =0.001 rd/s
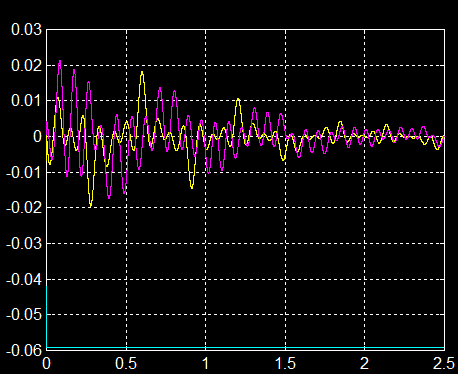
Dépointage spécial de z par rapport au Nadir Z ( spécification respectée )
Vitesses angulaires absolues( en °/s ) avec notamment q =- 0.06 °/s soit - 0.001 rd/s
NB : nous retrouvons la stabilisation parfaite en attitude Y-Thomson idéale
On voit bien apparaître, sur les composantes 1 et 3, un rappel amortisseur des nutations transverses wx et wy, un couple de rappel sur l'axe y du satellite, grâce au coefficient |B|, induisant de manière indirecte un contrôle de la roue qui travaille donc à vitesse quasi constante.
Logique de la composante 2 : Si h > href, la roue tourne trop vite, le couple de commande satellite sur l'axe y est donc < 0. Ce couple a tendance à diminuer la vitesse angulaire satellite q, la roue va donc, par réaction, compenser pour "contrer" et donc exercer un couple pour augmenter q, donc la roue reçoit du satellite un couple opposé c'est à dire < 0, qui fait donc diminuer h. C'est une bonne logique !!!
En clair ce fonctionnement de la roue à vitesse constante est une désaturation de la roue en continu, évitant de programmer cette opération à intervalles réguliers.
Dans un souci d'optimisation de la consommation électrique, il n'est pas nécessaire de supprimer comme à l'habitude ( voir ci-dessous ) la composante de M portée par B, car e est normal à B
Pour la roue, le couple de commande de la roue est C, la vitesse angulaire w. La logique de Steyn utilise l'angle q* entre z et Z, autant dire le dépointage de l'axe satellite par rapport au Nadir
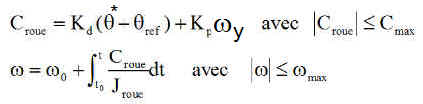
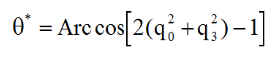
* Kx Ky Kz Kp Kd sont des gains constants, Jroue le moment d'inertie de la roue, wmax et Cmax vitesse et couple maximum admissibles pour la roue
* h= Jw est le moment cinétique instantané de la roue, w sa vitesse angulaire, wx et wy les vitesses angulaires relatives satellite de roulis et lacet
* h_ref est le moment cinétique de consigne de la roue ( censée travailler autour de sa vitesse de consigne de -600 tours/mn ).
1°) MISSION :
Le nanosatellite est chargé d'une mission de prise de vues, avec une caméra supportant un dépointage de 5° maximum.
Son orbite est choisie, juste au lancement (en passager secondaire) héliosynchrone:
- Altitude circulaire de 817 km
- Inclinaison de 98°.7
- Excentricité 0.0017
- Heure locale au nœud ascendant 21 h 30
Aucun contrôle d'orbite, n'est prévu
Pour le respect de l'environnement, une désorbitation est obligatoire après 25 années de service???
2°) CONSIGNE D'ATTITUDE :
Le nanosatellite est prévu pointé zénith avec, nous l'avons dit, un dépointage toléré inférieur à 5°.
L'axe de plus grande inertie y aligné sur l'axe Y du repère orbital, celui qui porte la rotation orbitale. Donc x sur l'axe roulis X et z sur celui du tangage Z.
3°) EQUIPEMENTS POUR REALISER LE SCA :
On trouvera à bord:
- Une roue à inertie ci dessous une roue avec inertie estimée
|
Vitesse maximum |
6000 tours/mn |
|
Couple maximum |
4 10-6 Nm |
|
Moment d'inertie axial, première estimartion grossière |
3.2 10-5 kgm² |
On a un choix sur 3 roues
|
|
Type 1 |
Type 2 |
Type 3 |
|
Vitesse max ( tr/mn ) |
6000 |
16000 |
16000 |
|
Couple max (Nm ) |
6 e-4 |
23e-6 |
4e-6 |
|
Inertie axiale |
2.86 e-5 |
7e-7 |
1.2e-7 |
- Trois "magnétocoupleurs"
|
Puissance |
0.2 Am² |
|
Couple magnétique maximum |
3.3 10-7 Nm |
Voir aussi sur ce site
Informations disponibles à bord, en automatique, grâce aux magnétomètres et senseurs dédiés, ces équipements ne seront pas forcément présents, tout dépendra de la stratégie SCAO choisie avec le minimum de moyens :
|
Champ magnétique |
Composantes en repère satellite Dérivée en repère satellite |
|
Attitude |
Angles de position par rapport au repère orbital Vitesses angulaires par rapport au repère orbital |
- Un modèle de champ magnétique embarqué est possible. Il existe un modèle appelé IGRF ( International Geomagnetic Reference Field ) qui fournit les composantes, Est, Nord, Zénith du champ magnétique moyennant la connaissance de la date, et de la position géocentrique ( altitude, longitude et latitude )
Voir lien 1 lien 2 ( pour un calcul ponctuel ) lien 3 ( ponctuel ) lien 4 ( routines Matlab )
- Moyens de calcul classiques avec informatique et électronique dédiées ( numérique + analogique )
4°) DONNEES INERTIELLES ET MASSIQUE :
La matrice d'inertie du satellite, roue supposée bloquée sur le satellite S a pour coefficients ( version septembre 2015 )
Ir=22e-3;It=25e-3;Il=10e-3;Irt=5.344e-5;Irl=-1.998e-4;Itl=9.839e-4;
Elle est susceptible de modifications mineures, au cours de l'avancement du projet.
La masse du satellite est approximée autour de 3 kg, peut-être moins.
5°) ESTIMATIONS DES PERTURBATIONS :
Le lecteur se documentera sur les origines diverses des perturbations. Nous ne donnons qu'une valeur approximative pour chaque type. Divers projets réalisés par des étudiants permettront d'affiner le calcul des perturbations.
|
Couple aérodynamique |
< 4 10-8 Nm |
|
Gradient ( voir page dédiée ) |
A calculer |
|
Couple radiation solaire |
< 5 10-8 Nm |
|
Couple magnétique résiduel, très difficile à cerner |
< 5 10-7 Nm |
Surface à prendre en compte pour la traînée ou la pression de radiation solaire S = 2 dm².
Angles de Cardan
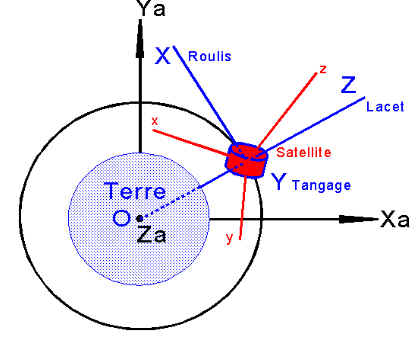
Xa Ya Za un repère absolu ou inertiel.
XYZ est le repère de consigne, pour nous ce sera le repère orbital : X suivant la vitesse, Y suivant le moment cinétique orbital, Z le zénith.
xyz est un repère lié au satellite, adapté à sa géométrie. Ci-dessous le repérage par angles de Cardan.
|
|
X Y Z repère orbital x y z repère lié au satellite
|
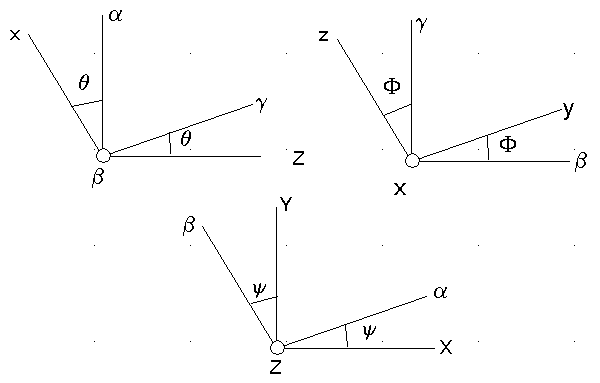
NB: Les festons sont dus aux produits d'inertie


Deux courbes qui confirment l'alignement de l'axe de soin ( tangage y ) sur la normale Y au plan orbital
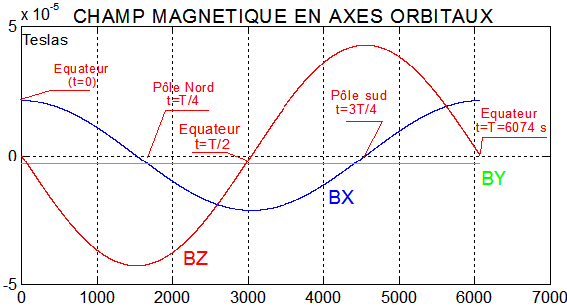
Le modèle de champ magnétique orbital est correct
A : EXACTITUDE DE L'INTÉGRATION ET ERREURS D'ARRONDIS :
K_perturbation=0;
% 0 sans perturbation 1 avec perturbation
K_commande=0;
% 0 sans commande 1 avec commande
K_inertie=1;
% 0 pour une matrice d'inertie quelconque 1 avec matrice réelle
K_revolution=0
;
% 0 pour une matrice d'inertie quelconque 1 pour une matrice de révolution autour de y
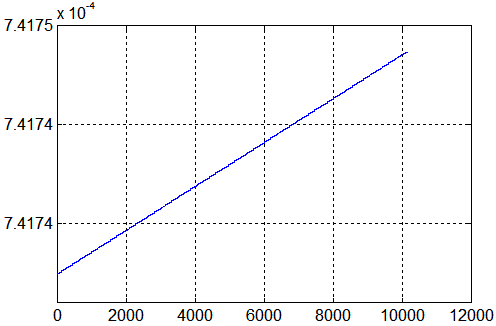
L'énergie cinétique (J) se conserve à une précision relative de 1.4 e-5
ou absolue de 1 e-8 joule pas de 0.2 à 1 s max
B : EXACTITUDE DU MOUVEMENT DE POINSOT AVEC MATRICE D'INERTIE DE REVOLUTION :
K_perturbation=0; % 0 sans perturbation 1 avec perturbation
K_commande=0; % 0 sans commande 1 avec commande
K_inertie=0; % 0 diagonale 1 avec matrice réelle
K_revolution=1; % 0 pour une matrice d'inertie quelconque 1 pour une matrice de révolution autour de y
On retrouve bien que la rotation transversale (p²+r²)^0.5 se conserve et que la rotation axiale q se conserve q=q0
C : EXACTITUDE DU REPOS COMPLET ET DE LA FORMULE DONNANT L'ANGLE (Y,y) :
K_perturbation=0; % 0 sans perturbation 1 avec perturbation
K_commande=0; % 0 sans commande 1 avec commande
K_inertie=0; % 0 diagonale 1 avec matrice réelle
K_revolution=1; % 0 pour une matrice d'inertie quelconque 1 pour une matrice de révolution autour de y
K_repos=1; % 0 pour le cas général et 1 pour le repos total
Le repos reste parfait sur un essai de 5000 secondes. L'angle (Y,y) reste nul sur ce même temps
D : EXACTITUDE DU MOUVEMENT CONIQUE DE POINSOT ET DE LA FORMULE DONNANT L'ANGLE (Y,y) :
Matrice de révolution --> Ir=16e-3;It=25e-3;Il=16e-3;Irt=0;Irl=0;Itl=0;
Position initiale de pointage parfait avec y sur Y --> roulis0=0;tangage0=0;lacet0=0;
Petit roulis et spin en tangage --> v_roulis0=0.00524;v_tangage0=0.1;v_lacet0=0;
L'axe doit décrire un cône qui repasse régulièrement toutes les périodes de Poinsot, par le pointage idéal, avec une ouverture de
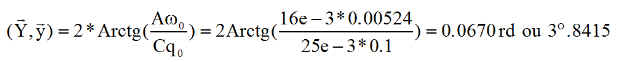
La période est de
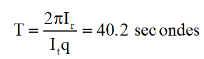
ce que confirme le graphe suivant
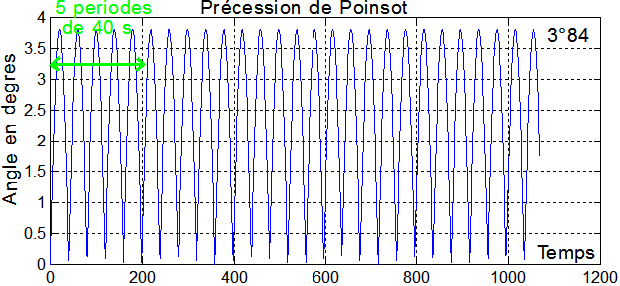
E : MOUVEMENT SOUS L'ACTION DES SEULES PERTURBATIONS :
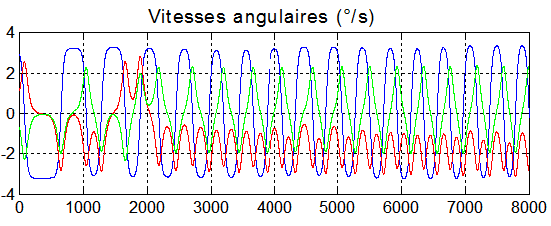
Il n'y a pas de divergence notable.

