Remarque initiale : J'ai essayé dans mes premières simulations de traiter  le pointage fin avec un contrôle des axes presque séparément, à savoir une bobine de tangage pour roulis et lacet ensemble lors des passages équateur ( pour le lacet ) et pôles ( pour le roulis ), et le tangage traité isolément avec une roue.

Les simulations ont toutes bien fonctionné au départ au dessus de l'équateur et les angles se sont mis à diverger au dessus des pôles en particulier.

J'ai fini ( je crois ) par comprendre que les couplages entre composantes du champ magnétique, sur les axes secondaires non traités par la régulation, ne permettaient pas le contrôle global. Une autre approche où les axes sont traités simultanément, est nécessaire

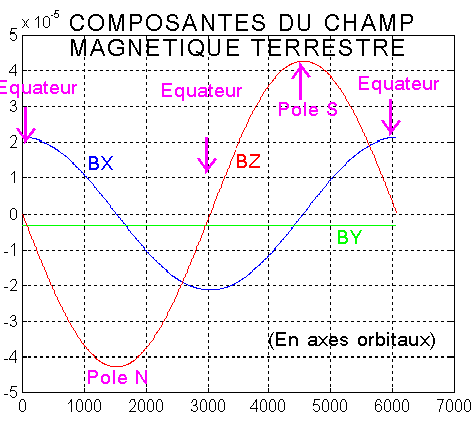
. Seul outil externe utilisable : le champ magnétique terrestre. Ci dessous une représentation approchée analytique, sur une période de 6074 secondes ( celle du nanosatellite, du moins pour l'orbite initiale ).

I CONTROLE A 3 MAGNETOCOUPLEURS :

Partons de l'équation d'état du satellite :

U est la matrice colonne des couples externes, comprenant les couples perturbateurs Cpert et le couple de commande Ccom.

1°) Principe de la commande :

Les 3 angles d'attitude roulis F, tangage q, lacet Y, sont contrôlés classiquement par un rappel proportionnel, dérivé, intégral  ( noté PID ou PD suivant le cas )

Remarque : Comme les angles sont petits, le contrôle sur les axes x y z coïncide bien avec celui sur les axes de masure des angles )

Le schéma bloc est ainsi choisi, ci-dessous en PD pour le roulis, en entrée l'écart à la consigne, en sortie la génération électronique du PID affectée ou non de retard ou d'un filtre et d'un gain. Beaucoup de paramètres à régler.

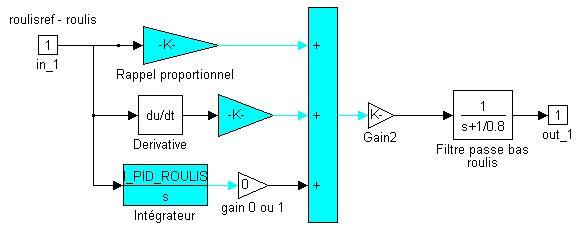
Nous noterons par exemple pour le tangage q , le couple généré sur l'axe tangage ( le signe - est inclus dans le PID ) pour obtenir des équations du style simplifié

Ainsi le vecteur U se présente sous la forme :

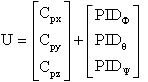
2°) Mise en forme mathématique de la commande.

Moyens utilisés : 3 magnétocoupleurs, disposés suivant les 3 axes x y z du satellite,  de moments magnétiques respectifs: mx, my, mz, qu'il faudra programmer ( capteurs + électronique + informatique en temps réel ) à l'aide des informations disponibles à bord:

- De capteurs de position ( éventuellement de vitesse )

- De la connaissance du champ magnétique dans le repère orbital, qui permettra donc le calcul du champ en repère satellite, ( éventuellement de sa dérivée du champ en axes satellite)

- D'une source d'énergie ( panneaux solaires + batterie ) pour alimenter les 3 bobines

- D'une électronique + informatique, pour l'alimentation et la surveillance de la saturation des bobines ( limitation des courants ou de la puissance )

Nous partons du calcul du moment crée par un magnétocoupleur placé dans un champ magnétique de valeur locale B

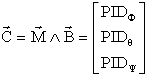
Cette écriture ne permet pas facilement de déduire les moments magnétiques respectifs de chaque bobine. Mettons la relation sous forme matricielle ( avec la représentation classique de l'opérateur calcul vectoriel ):

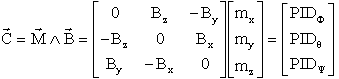
ATTENTION:

Premier écueil: :Il est clair que le couple C ne pourra jamais être colinéaire au champ B. Ce qui signifie qu'on ne peut pas appliquer de couple parallèle au champ magnétique, on est face à une singularité .

Deuxième écueil  : la matrice du champ a un déterminant nul, et n'est donc pas inversible. Le système ne peut avoir de solution que si C est orthogonal à B ( évidence au départ ), par contre cette écriture permet d'avancer pour la solution que nous cherchons.

II COMMANDE A 2 MAGNETOCOUPLEURS ( axe roulis & lacet ) + 1 ROUE SUR L'AXE TANGAGE  

C'est la proposition retenue pour le nanosatellite. On libère un axe, pour nous celui du tangage, sur lequel on place une roue, commandée à part et pilotant le tangage, pour l'essentiel.

Pourquoi le tangage, plutôt qu'un autre axe? Tout simplement parce que la mission demande soit un pointage zénith soit un pointage nadir. Avec la roue sur un axe normal au plan orbital, on pourra plus facilement utiliser son moment cinétique qui devrait s'aligner sur la normale orbitale et stabiliser l'attitude.

1° La théorie :

On souhaite commander chacun des 3 axes avec une loi de commande spécifique, dont le type peut être quelconque ( PID ou PD ou certains PID et d'autres PD etc...). Choisissons par exemple le type PID comme défini plus haut. 

Donc, on utilise un couple de roue de réaction  ( sur le tangage ) avec un couple magnétique sur les autres axes. Les bobines disposées sur les axes x et z donneront toujours un couple car le champ magnétique reste pratiquement dans le plan orbital, oscillant de l'axe Z vers l'axe X, tout au long de l'orbite

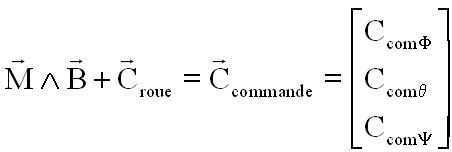
a) Une roue tangage + 2 bobines roulis lacet:

Ainsi avec la roue sur le tangage et les bobines sur les autres axes de moments magnétiques mx et mz à déterminer, on a :

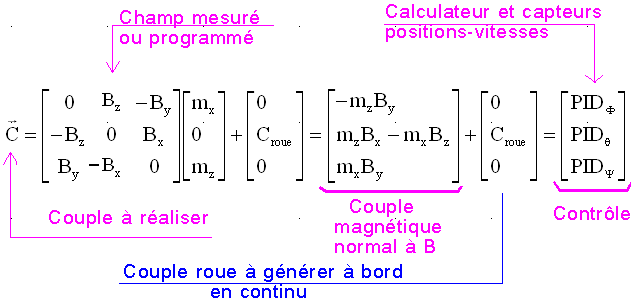
On peut écrire une relation  équivalente :

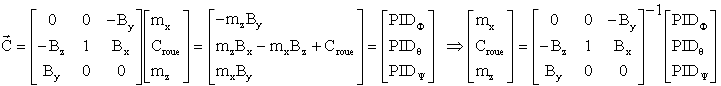
Maintenant, la matrice associée au champ est inversible ( déterminant = (B_y )²    ( carré de la composante sur l'axe tangage ) qui n'est jamais nul sur notre orbite, en mode petits angles et même pratiquement constant avec notre représentation analytique du champ )

La résolution directe donne des relations particulièrement simples:

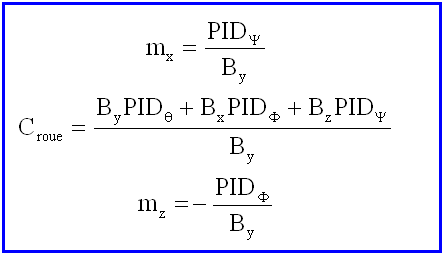
Vérifications :

1 La relation  vue plus haut scalairement multipliée par B donne

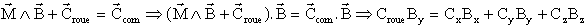
qui vérifie bien la valeur de Croue

Ces formules ne semblent plus poser de singularités, le long de l'orbite. Cette manière d'utiliser le champ ne fera plus apparaître de composantes parasites sur les axes annexes à celui qui est contrôlé en principal.

NB1 : Tout à fait normalement, c'est mx avec Bz ou mz avec Bx qui contrôleront le tangage lors du survol du pôle ( resp  le survol de l'équateur )

NB2 : On notera l'amplification des PID ( 1/By = 300000, Bx/By = 11, Bz/By  = 22 

NB : L'essai de cette formulation sera testé dans la simulation ==> regdesat.m, vue des résultats par visusim2.m (angles et vitesses ) ou directement dans la simulation.

REMARQUE A POSTERIORI :

C'est en relisant ce qui vient d'être écrit, que j'ai réalisé que l'on pouvait s'affranchir de la division par la composante By, qui n'apparaît que comme l'inverse d'un gain pour les 3 PID. On pourrait donc choisir sans dommage les moments magnétiques suivants:

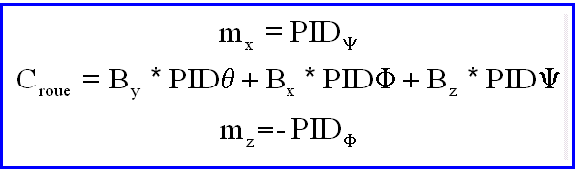
Cependant pour une orbite polaire, By est pratiquement nulle ou nulle suivant le modèle et donc il y aurait lieu d'étudier plus en détail la régulation. Comme ce n'est pas notre cas, je repousse à plus tard cette étude.

b) Une roue tangage + 2 bobines roulis tangage:

Une étude analogue donnerait

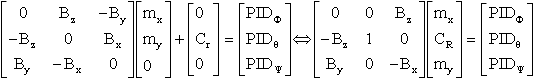
Là encore la matrice associée à B est inversible presque partout, car de déterminant By Bz, mais une singularité apparaît 2 fois par orbite, lors du survol de l'équateur.

Donnons quand même les formules des moments et couple roue à commander

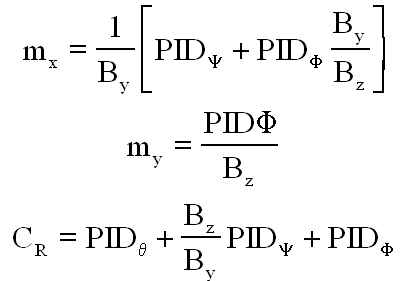
b) Une roue tangage + 2 bobines lacet  tangage:

Donnons le résultat, avec toujours une singularité au survol des pôles

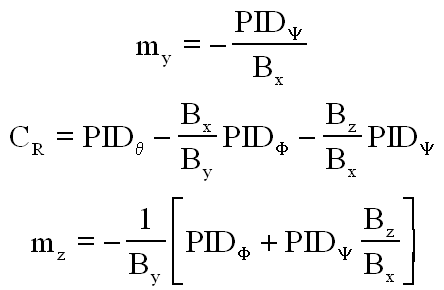
CONCLUSION :  Pour éviter tout souci, c'est la première option que je conserve, une roue sur le tangage et 2 bobines roulis lacet

REMARQUE SUR LA SATURATION :

Les technologies des bobines ou de la roue, limitent les conditions d'utilisation de ces actuateurs/

- Roue : Couple maximum de 4e-6 Nn  donc | Cr  | < 4e-6

- Magnétocoupleurs de moment magnétique  < 0.2 Am²  donc Sup( | mx |, |mz |) < 0.2

On ne peut se contenter de mettre un seuil de saturation sur chaque actuateur, car on comprend bien que si mx et mz dépassent le seuil admissible, on ne peut pas imposer mx = mz = 0.2 Am². On n'aurait plus une solution admissible.

Par contre on peut travailler en respectant les proportions, c'est à dire qu'une fois le calcul de mx, mz, Cr effectué à chaque pas de la simulation, on peut ramener l'ensemble des actuateurs dans leur plage de fonctionnement acceptable, ceci par une correction proportionnelle, avec la fonction  y=saturmmc.m et des notations suffisamment explicites:

maxi=[abs(mx/moment_max_bobine),abs(mz/moment_max_bobine),abs(Croue/couple_max_roue)];

coeff_max=max(maxi);

if coeff_max>=1

mz=mz/coeff_max;
mx=mx/coeff_max;
Cr=Croue/coeff_max;

end

Si toutes les valeurs sont dans la bonne plage, on les garde. Retrouver la fonction

2°) Premiers résultats :

Avec la simulation on obtient les premières courbes ( valables sur plusieurs périodes ) des angles

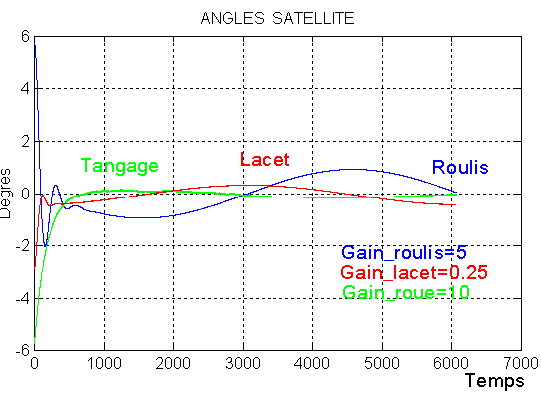
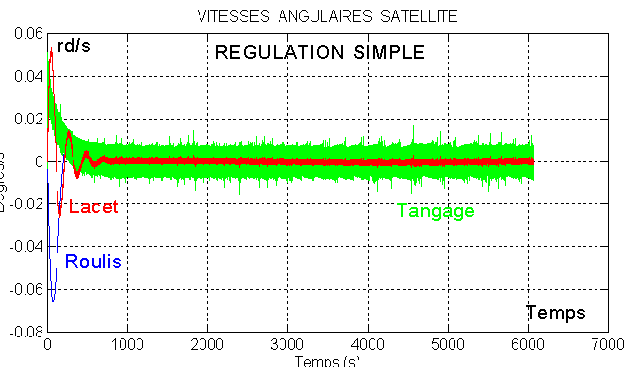
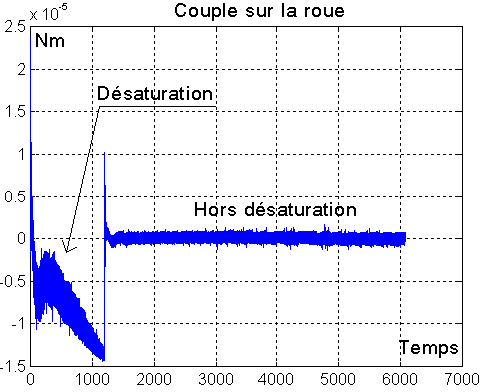
Valeurs acceptables, hors saturation

NB faudra prévoir une baisse du gain en désaturation, d'un facteur 10?

III MISE EN PLACE DE LA DÉSATURATION DE LA ROUE : 

1°) Origine du problème :

Un satellite en orbite est soumis à la gravité, qui détermine sa trajectoire et à des forces annexes, petites qu'on appelle des perturbations d'origines diverses

    - Aérodynamiques

    - Rayonnement et vent solaire

    - Champ magnétique terrestre interagissant avec les courants circulant dans le satellite

    - Gradient de gravité, dépendant de la géométrie inertielle du satellite

Ces actions n'ont pas un effet moyen nul et donc il reste sur certains axes des composantes permanentes qui ont pour effet de faire dériver les paramètres toujours dans le même sens en moyenne. C'est souvent le cas de la perturbation aérodynamique qui agit sur le tangage. Comme la roue "contre" ce couple pour maintenir une consigne fixée de tangage, sa vitesse angulaire va augmenter ou diminuer toujours dans le même sens.

Quand cette vitesse angulaire atteint une valeur maximale, fixée par la technologie de la roue, on dit que la roue est "saturée".

Il faut alors la "désaturer" en ramenant sa vitesse à l'opposé de la valeur maximale atteinte. Fort heureusement cette opération de désaturation n'est pas effectuée encontinu, mais seulement quand la vitesse devient trop importante.

2°) Premier essai :

Nous restons dans l'esprit de la régulation précédente qui fonctionne parfaitement. 

a) Le moyen :

Donc, nous demandons aux magnétocoupleurs d'assurer en plus du contrôle de l'attitude, la désaturation de la roue, en ajoutant un couple à exercer sur la roue pour la "désenrouler" d'une vitesse basse vers une vitesse haute. Le couple est donc > 0, les bobines se chargeant d'exercer le couple opposé sur le satellite.

b) Calculs d'estimation:

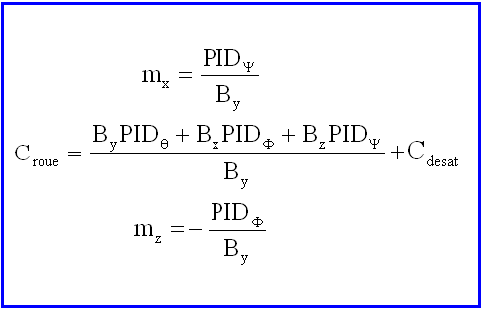
La roue est donnée pour une vitesse maximale de 6000 tours/mn, soit 100 t/s ou encore 630 rd/s.

Le couple maximum admissible est de 4e-5 Nm, nous pouvons raisonnablement en garder 50% pour la désaturation, laissant l'autre 50% pour le contrôle fin.

Donc nous disposons d'un couple Cdesat de 2 e-6 Nm

Calculons la durée D de l'opération 

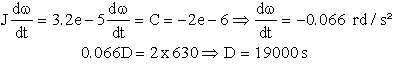
La désaturation demandera en continu 3 périodes,  soit grosso modo 5 à 6 heures.

Cette durée est un minimum, car le contrôle doit rester correct, nous autorisons un dépointage angulaire de 0.07 rd, environ 4°.

Les bobines profitent au maximum du champ magnétique lors du survol de l'équateur ( composante Bx ) et du pôle ( composante Bz ). Comme Bz est 2 fois plus grande que Bx, si on veut " lisser" la contribution ( par leur moment magnétique ) des bobines, on diminue le couple de celle qui travaille avec Bx par rapport à celle qui travaille avec Bz, ce qui leur demande sensiblement le même moment magnétique.

J'ai choisi la formule suivante moyennant la convention t=0 à l'équateur.

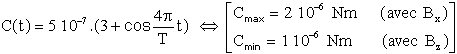
Ma première simulation a été" catastrophique, car au moment du déclenchement de la désaturation, le couple démarre brutalement, conduisant les PID à prendre des valeurs énormes à cause d'une dérivée presque infinie.

L'ayant compris, j'ai choisi de lisser la montée en régime ( un automaticien averti fera mieux que moi !!) en utilisant une montée accompagnée d'une exponentielle partant de 0 et convergeant vers 1. Le succès a été frappant!!

Voici la fonction utilisée :

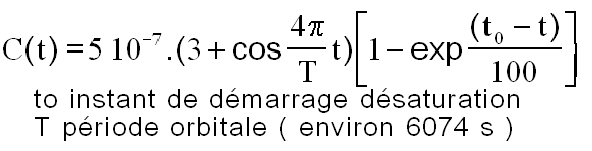
NB : J'espère que quelqu'un m'apportera une solution plus pertinente. Effectivement, une solution m'a été suggérée qui pourrait consister à utiliser des séries de Fourier qui, avec un nombre fini de termes, qui  permettent une dérivation correcte

c) La simulation sur 3500 secondes : Valeur choisie, car la simulation se met à diverger à l'approche du survol du pôle sud. Pourquoi? A trouver encore?:

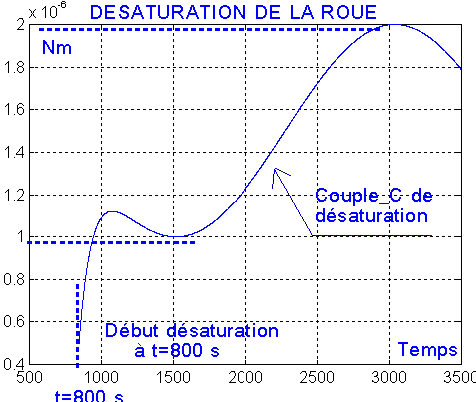
NB : la simulation montre qu'effectivement ce couple oscille entre 1 et 2 e-6 Nm, ce qui avait été prévu. Seul le départ est bosselé" ( exponentielle non complètement étalée )

d) Le contrôle des paramètres:

Simulation complète regdesat.m paramétrée par scadesat.m  Télécharger les programmes Matlab

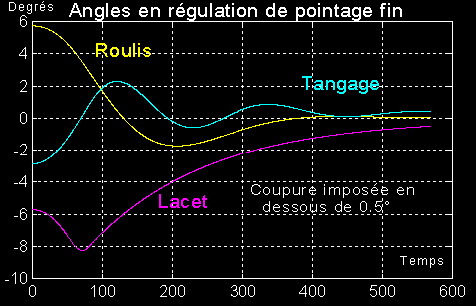
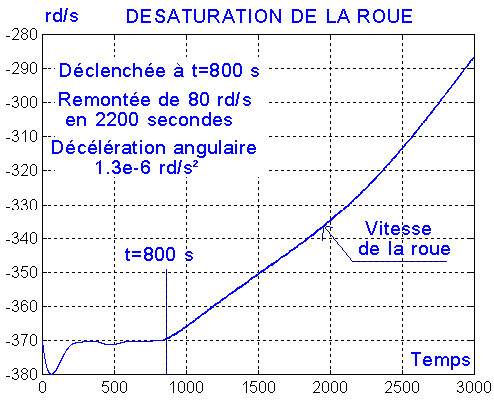
Le contrôle est resté excellent durant 20000 secondes en désaturation. Les angles sont restés confinés dans une bande de 1°.6 autour de 0.

La désaturation que j'ai débuté à -360 rd/s ( 57 tours/s ou 3440 tours/mn ) a remonté la vitesse de la roue jusqu'à 40 rd/s soit 380 tours/mn en 17000 secondes soit 3 périodes.

 e) Vérifications des spécifications:

Ce travail devra méticuleusement être réalisé, pour garantir la bonne marche du système. Je le commence en partie.

1 - Le niveau du couples de commande de la roue :

 Approche 1 :Estimation par le calcul en fin de séquence désaturation

TMC de la roue 

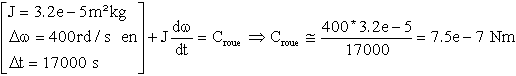
Le résultat n'est que de 20% du couple autorisé. On peut après confirmation le vérifier sur toute la désaturation

Étonnant, : le graphe ci-après donne le couple " imposé" au satellite, pour obliger la roue à travailler, et ce couple qui varie de 1 à 2 e-6 Nm est plus grand que celui commandé à la roue.

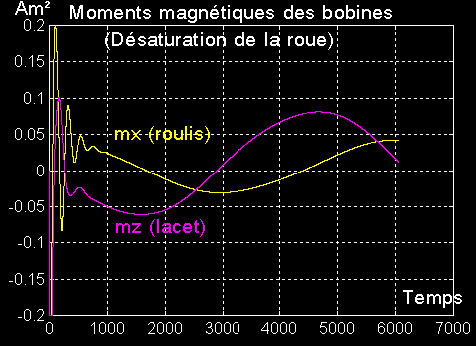
2 - Le niveau des moments magnétiques des bobines  en désaturation :

Les courbes montrent, qu'à part le départ de la régulation, les magnétocouplleurs travaillent à 50% de leur potentiel.

On voit très bien que le niveau de travail des 2 bobines est analogue, ce qui prouve le bien fondé du choix de la fonction couple C(t) 

On constate aussi que les bobines étalent leur travail en alternance pôle - équateur

ANNEXES ( Sources - calculs détaillés - programmes)

LISTE DES VARIABLES DE L'ESPACE PMATLAB

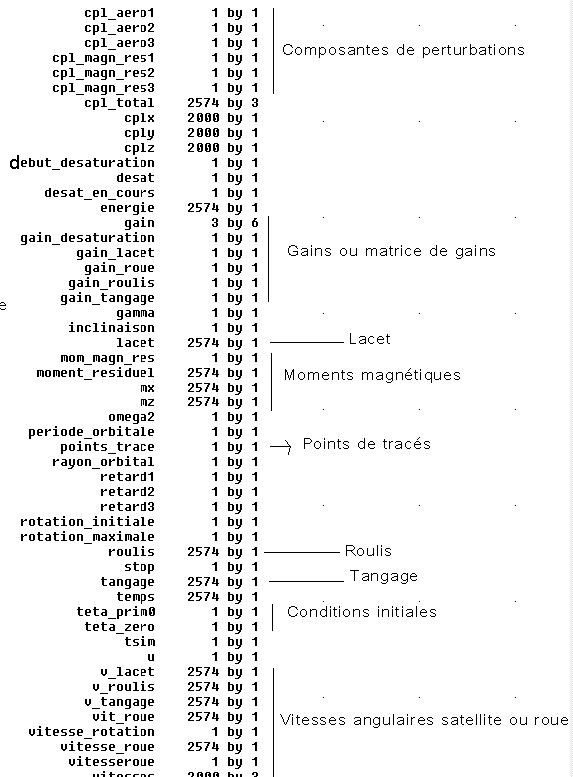
ANNEXES :

Fonctions utilisées:

1--->   liss_cpl.m

function y=liss_cpl(u,debut_desaturation,periode_orbitale);

% Cette fonction est destinée à éviter le front raide de début de couple
% pour ne pas avoir de dérivée infinie dans le PID

y=5e-7*(3+cos(4*pi/periode_orbitale*u))*(1-exp((debut_desaturation-u)/100));

end

Guiziou Robert décembre 2013