SIMULATIONS AVEC MATRICE D'INERTIE NON DIAGONALE
APPLICATION DU TMC ( CAS PETITS ANGLES )
![]()
|
Janvier 2013 III CONSEQUENCES DE LA PRESENCE DE LA ROUE
|
|
![]()
A - DONNÉES NÉCESSAIRES AUX SIMULATIONS :
|
|
Données
nanosatellite |
|
|
Asat |
|
Matrice
d'inertie du satellite ( 3x3 ) |
|
Altitude_orbite |
817 |
Altitude
sol en km |
|
rayon_orbital |
(6378+altitude_orbite)*1000 |
Rayon
orbital en m |
|
vitesse_rotation |
sqrt(39.86e13/rayon_orbital^3) |
Vitesse
angulaire ( rd/s) |
|
inclinaison |
98.7*pi/180 |
Inclinaison
en rd |
|
|
Cham magnétique |
|
|
BX BY BZ |
Données analytiques |
Composantes
calculées |
|
|
Paramètres simulation |
|
|
tsim |
Saisie dans fichier initialisation |
Durée
simulation ( s ) |
|
Points_trace |
Saisie dans fichier initialisation |
Nombre
de points du tracé |
|
|
Données
roue |
|
|
J |
3.2
e-5 |
Inertie
axiale de la roue ( à vérifier car estimée
) en kg-m² |
NB : Avant tout calcul,
vérifions que Asat est bien une
matrice d'inertie possible, c.à.d qu'elle a des valeurs propres >
0 , on peut
alors avoir:
Les
valeurs propres à inerties
principales
Les
vecteurs propres à axes
principaux d'inertie. Dans Matlab ( ce que j'utilise )
[V,D]=eig(Asat)
V =
[ axes principaux ] à très proches
des axes x y z actuels
-0.9993 -0.0263
0.0248
-0.0318 0.9661
-0.2564
0.0173 0.2570
0.9663
D =
[ moments principaux ]
0.0320 0
0
0 0.0371
0
0 0
0.0209
B - LES BASES DES CALCULS MATLAB, EN MODE POINTAGE FIN
( angles et vitesses petits ), application du TMC:
Comme les magnétocoupleurs sont disposés en alignement avec
les axes satellite, le calcul des couples magnétiques demande les composantes
du champ magnétique ( noté B ) en axes satellite.
Le champ magnétique est connu
à
dans la réalité par des magnétomètres à bord et donc directement en axes
satellite
à
dans la simulation par un modèle analytique en axes orbitaux ( dont il faudra
valider la qualité )
J'ai construis, pour l'orbite donnée, les composantes du champ magnétique terrestre, fonction du temps, donc de la position, à l'aide d'une fonction du temps, délivrant sous Matlab, les 3 composantes dans le repère orbital. C'est y=champmgn.m. La récupérer
Pour une simulation plus précise, un modèle de champ embarqué est possible ( voir modèle IGRF )
Pour les angles nous adoptons l'ordre 1 - 2 - 3 pour F
- q - Y ou encore Roulis
- Tangage - Lacet
|
|
X Y Z repère orbital x y z repère lié au satellite Avec l'hypothèse petits angles on a
|
Le bloc de simulation du comportement en attitude est champsat.m
a) Moment cinétique ( mode pointage fin = petits angles et petites vitesses )
On se place dans le cas le plus complet, satellite + roue
d'inertie ( Moment inertiel = J, vitesse notée w
) sur l'axe tangage
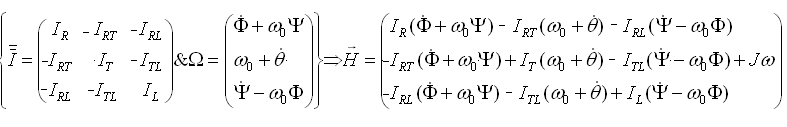
b)
Théorème du
moment cinétique :
Dérivation absolue, traduite en repère inertiel.
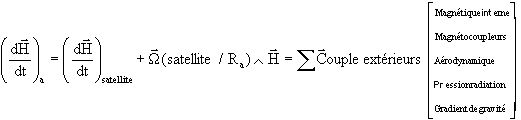
c)
Traduction en
3 équations scalaires :
Calculs plutôt lourds, dans lesquels on néglige les
produits de vitesses et d'angles, du second ordre par rapport aux termes linéaires
conservés.
Rappelons ce que vaut le couple du gradient de gravité.
Voir explications
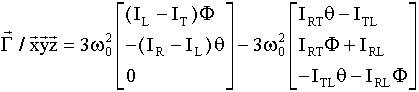
Pour des angles
inférieurs à 0.1 rd, le premier couple a des composantes maximum de l'ordre de
8 e-9 Nm, le deuxième 2 e-9, donc pour l'ensemble un maximum de 10-8
Nm
3 - MISE SOUS FORME CANONIQUE :
a)
Pour mettre en œuvre une simulation Matlab, une façon de fonctionner est de mettre le
système général sous la forme matricielle suivante :
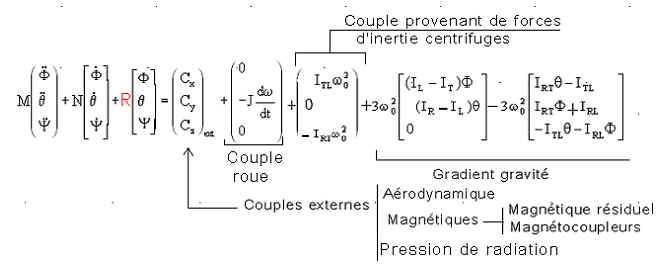
|
Dans
la partie de l'équation ci-dessus, ce terme
pourrait
être négligé devant le couple résiduel magnétique, de maximum est
annoncé 4.5 e-7 Nm Rappel
: ( Période
T = 6073 s ) |
Le
couple ci-dessous est le couple réactif de la roue sur l'axe
tangage du satellite
|
La
partie gradient de gravité est de l'ordre de 10-8 à 10-9
Nm, pour des écarts angulaires maximum de 0.1 rd
|
devenant,
après intégration, au premier membre, du terme prépondérant du gradient :
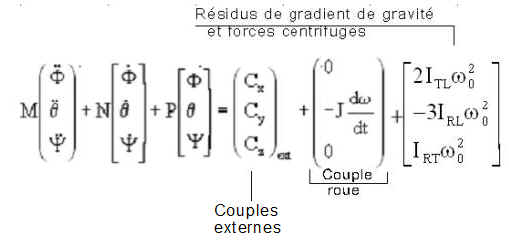
|
|
N est antisymétrique. Comme le système libre ne comporte pas d'amortissement ni interne ni externe, les termes avec les dérivées proviennent de couplages gyroscopiques ne dépensant pas d'énergie. |
|
|
|
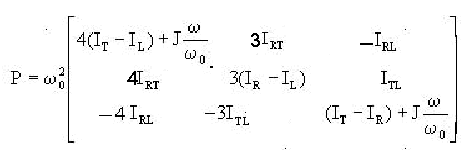
Dans les simulations on calculera w = vitesseroue, qui sera injectée dans le calcul des matrices :
M
= Asat N=K_SAT+vitesseroue*H_SAT
P= L_SAT+vitesseroue*Q_SAT
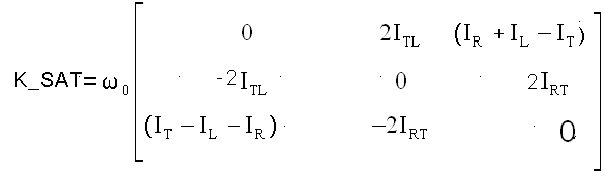
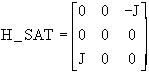
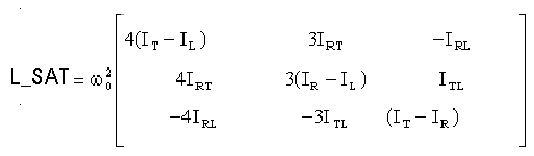
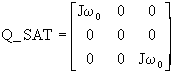
Le lecteur se convaincra qu'en passant au vecteur d'état
X ( à 6 composantes ), on obtient :
X est le vecteur d'état
Y le vecteur de sortie
avec
|
|
|
|
|
|
|
Matrice 6X3 |
des
couples actifs perturbations |
La simulation la plus complète a pour nom regdesat.m initialisée par scadesat.m, que vous pouvez retrouver dans le pack de fichiers regdesat.zip à télécharger et à exécuter dans le répertoire de décompression
POSITION
D'EQUILIBRE EN REPERE ORBITAL :
La
présence de termes constants au second membre, indique qu'une position d'équilibre
où les angles sont nuls, est impossible. Ceci à cause des produits d'inertie.
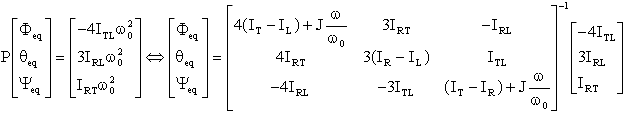
C:
ETUDE DES CONSEQUENCES POSSIBLESDE LA PRESENCE DE LA ROUE SUR L'AXE TANGAGE :
En
régime libre, le système aux petits angles est
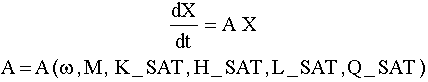
où
w
est la vitesse de la roue.
Le
calcul des valeurs propres ( 6 en tout, 2 à 2 conjuguées) peut donner des
renseignements utiles sur les pulsations propres du système.
[V,D]=eig(A)
avec V = [ axes principaux ]
et D = [matrice aux valeurs propres ]
J'ai
programmé la fonction y= pulsat(vit_roue,vitesse_rotation,Asat) avec
à vit_roue
est
la vitesse angulaire de la roue en rd/s
à vitesse_rotation, la pulsation orbitale en rd/s, donnée par l'initialisation
à Asat, la matrice d'inertie du satellite également donnée par l'initialisation
Par
exemple :
-
avec
une roue arrêtée, on trouve 3 périodes propres: T = 3925 s,
1570 s 6280 s ( proche de la
période orbitale)
-
avec
une roue à 6000 tours/mn dans un sens ou l'autre, on trouve T=6980 s, 6280 s et
8.2 s ( net raidissement )
Le système présente des valeurs propres à parties réelles nulles, montrant que les oscillations libres sont stables, quelle que soit la vitesse de la roue non surveillée.
SAUF GROSSE SURPRISE A VERIFIER : pour -1.81 < w < 0.129 rd/s, on trouve 2 valeurs propres conjuguées certes, mais réelles, donc conduisant à une instabilité ( pour la positive ), dont il faudra étudier l'importance. Voir ailleurs une formulation équivalente du problème
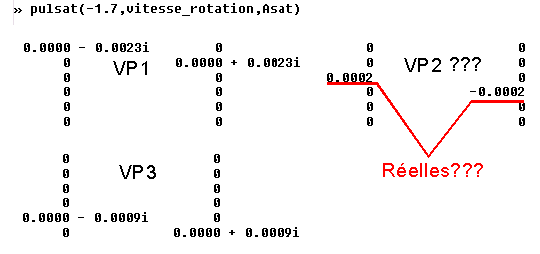 .
.
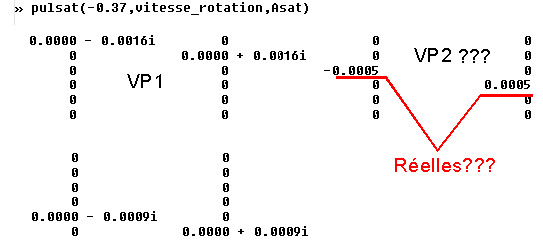
Etonnant à - 2 rd/s l'instabilité disparaît
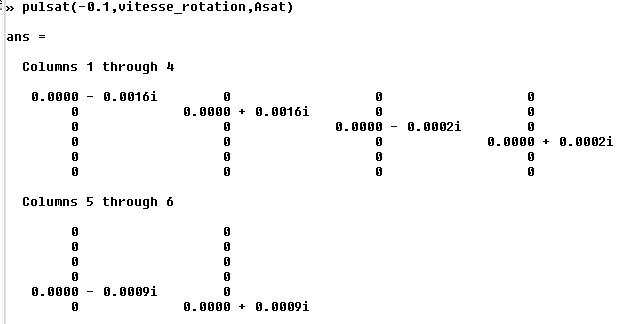
Ainsi qu'à - 0.1 rd/s

a)
Quelques
remarques toujours à propos de la roue:
1-
Dans la matrice N des dérivées, les termes N(1,3) et N(3,1) sont opposés,
traduisant des couplages gyroscopiques sans perte d'énergie, entre les
rotations roulis et tangage entre elles ainsi qu' entre la roue et les angles
roulis tangage.
2-
La stabilité libre du tangage est assurée par Ir > Il
3-
En l'absence de roue, le
rappel nécessite sur les angles roulis et lacet, It > Il et It > Ir.
Finalement on est assuré de la
stabilité des oscillations libres par
![]()
b)
Réflexion
sur le couplage gyroscopique roue-orbite :
Prenons l'équation en lacet et
supposons le satellite simplement dépointé en lacet de l'angle y ,. Comme le montre la figure 1.
|
|
|
Rappelons un principe de gyroscopie: quand un corps tournant
( la roue = gyro ), est monté dans un carter ( le nanosatellite ) lui même en
rotation, on peut supposer la roue bloquée sur son carter à condition de rajouter
aux couples extérieurs en jeu, un couple dit gyroscopique, qui tend à
aligner l'axe gyro sur l'axe de la rotation imposée ( effet gyroscopique )
|
Rotation gyro
|
Rotation
carter
|
Couple
gyroscopique
|
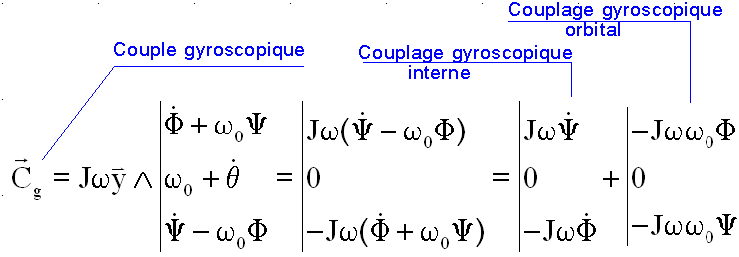
C'est donc bien l'origine du terme
Jwwo Y
que l'on trouve dans l'équation en Y.
Il en est de même de l'équation en F.
c)
Conséquences
de ce couplage
:
Les 2 couples gyroscopiques tendent à agir sur le satellite
pour aligner l'axe roue sur l'axe tangage, ce qui est bénéfique si ces 2 axes
sont de même sens, mais gênant si les axes sont proches de 180°, car il
pourrait y avoir danger de retournement, surtout à vitesse de roue élevée.
Ordre de grandeur de ce couple
avec une roue à 400 tours/mn, la valeur maximale( lorsque les 2 axes sont
orthogonaux ) est :
(Cg)max
= 3.2 e-5 *400*2*pi/60
* 2pi/6070 = 7 e-5 Nm
conduisant
sur l'axe de lacet à une accélération maximum en lacet
de
Cg/Il
= 7 e-5 / 22 e-3 = 3 e-3 rd/s²
urait une accélération moyenne ( max quand Y=90°, nulle quand Y=0°) de 1 à 1.5 e-3 rd/s², soit après 2 intégrations à un angle Y
= 6 e-4 t²,
Le rattrapage de 90° pourrait se faire en 1 minute ( Calcul
à valider, car approximations )
Cet inconvénient est-il utilisable dans les phases survie ou
acquisition? C'est
à voir, je n'en sais rien pour le moment.
4-
A
étudier sérieusement :
Les termes de rappel élastique
( sauf erreur de ma part, c'est pour cette raison que j'aimerais que l'on valide
mes calculs)
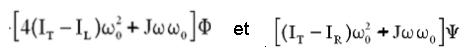
dans les équations roulis et lacet, peuvent être < 0 suivant l'évolution de la rotation de la roue. Si les calculs sont corrects, il y a matière à un petit souci. Effectivement, il y a une plage de vitesses [ de - 1.81 rd/s à - 0.129 rd/s ] avec une instabilité possible ( voir plus haut ). Le plus surprenant, c'est que ce n'est pas à grande vitesse. Alors pourquoi?
- On comprend bien que pour une grande vitesse positive de la roue, l'effet soit stabilisant. C'est la "l'effet gyroscopique"
- Or pour de grandes vitesses négatives de la roue, il en est de même. L'explication tient à ce qu'on appelle la "rigidité gyroscopique". Le retournement ne se fait pas pas pour la raison suivante. Reprenons la figure vue plus haut, pour la compléter.
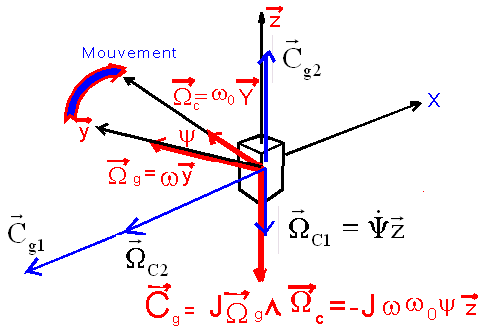
Le premier décalage y en lacet, crée un premier couple gyroscopique Cg, qui "amorce" une rotation autour le l'axe z. Cette rotation WC1 crée un deuxième couple gyroscopique Cg1 qui "engage" une rotation WC2 autour de lui.
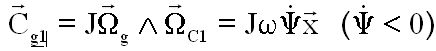
La rotation secondaire crée un couple gyroscopique Cg2 qui vient s'opposer au tout premier, annulant ( si la vitesse est très grande ) l'effet de Cg. C 'est la notion de " rigidité gyroscopique"
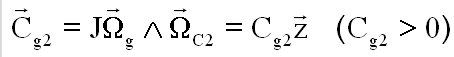
C ) PREMIERES SIMULATIONS DE MISE AU POINT:
Dans un premier temps, au vu des équations relativement lourdes,
j'essaye de vérifier que la simulation est correcte, en prenant le cas plus
simple:
D'une matrice d'inertie diagonale, donc beaucoup de termes
parasites hors diagonale disparaissent
Avec un modèle sans roue
Avec un modèle sans magnétocoupleuirs
Sans perturbations, en ne gardant que le gradient de gravité,
du moins ce qu'il en reste classiquement.
Ce sera le modèle des "OSCILLATIONS LIBRES SOUS
GRADIENT DE GRAVITE" dont j'ai déjà obtenu des résultats il y a quelques
années. La validation prendra alors tournure.
a) Les équations à traiter :
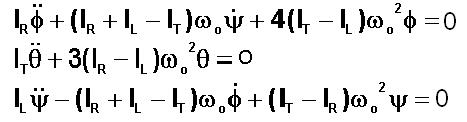
b) Pour vérifier le résultat :
Si on multiplie chaque équation par la dérivée du paramètre
principal de cette équation et qu'on somme et on intègre, on obtient
une intégrale première classique liée à l'énergie mécanique.
![]()
On y trouve en partie l'énergie cinétique dans le premier
terme et l'énergie potentielle ( en partie ) du couple de gradient de gravité.
Cette constance peut servir de test pour les premiers pas d'une programmation.
NB : Comme tous les coefficients des dérivées au carré ou
des angles au carré sont positifs, on peut en déduire que les dérivées resteront bornées ainsi que les angles.
Ce qui est un gage de stabilité. Les écarts à zéro seront d'autant plus
petits que l'énergie initiale le sera, bien évidemment.
Guiziou Robert janvier 2013
![]()