DYNAMIQUE DU NANOSATELLITE LIBRE  

ACTIONS DUES A LA ROUE ET POSSIBLE ZONE D'INSTABILITE

I  LES EQUATIONS DE LA MECANIQUE : 

1°) REPERES UTILES :

Sans refaire les figures: 

1 - Repère inertiel Ra

2- Repère orbital R, avec X suivant la vitesse tangente à l'orbite, Z  suivant le zénith, Y complétant la base ( normal au plan orbital )

3- Repère satellite Rs = ( x y z  ), lié à la structure rigide. C'est le repère dans lequel on écrit les équations du SCA seul, car l'orbite n'est pas contrôlée.

4 - u1, u2, u3  directions unitaires de 3 roues éventuelles ( notre cas ne comportera qu'une seule roue suivant l'axe tangage y ) 

2°) DONNEES: 

1 - Matrice d'inertie du satellite, roue supposées bloquée sur le satellite S

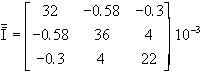
2- Roue de réaction:  

 J moment d'inertie axial de la roue

Remarque : 

Avec une accélération angulaire de 200 rd/s, pour atteindre 6000 tours/minute, en partant de -6000 t/mn, il faut un temps de fonctionnement total de 60 s.

Il faut donc prévoir une désaturation après un nombre d'impulsions de de durée totale 60 s.

3 - Magnétocoupleurs : 

Trois de prévus, un par axe, le moment magnétique total est M fournissant avec le champ magnétique terrestre un moment de commande

Sur l'orbite prévue, héliosynchrone à 817 km du sol, le maximum de champ magnétique est d'environ ( pour le modèle numérique approché ) de  43 10^-6 tesla

Avec un moment magnétique de 0.1 Am², le couple maximum sera de 43 10^-7   Nm ( à comparer à la roue !!!) 

Le graphe ci-dessous donne une période de révolution, avec passage à t=0 au nœud ascendant.   

3°) LE THEOREME DU MOMENT CINETIQUE : 

1 - Les angles :

L'attitude du satellite est représentée par 3 angles

:

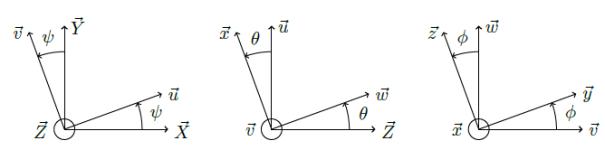Classiquement

Roulis f mesuré autour de x ( voisin de X lorsque les angles sont petits)

Tangage q mesuré autour de b ( voisin de Y lorsque les angles sont petits)

Lacet y mesuré autour de Z

2 -La rotation :

La rotation absolue est ( compte tenu de la rotation orbitale w₀ )

 La rotation qu'il faut annuler quand on souhaite obtenir un pointage Terre parfait est la rotation relative au repère orbital de composantes en roulis, tangage et lacet:

Dans le cas des petits angles en pointage fin ou en configuration nominale sous surveillance par SCA

NB1: Bien évidemment, on aurait pu utiliser les angles d'Euler ou une représentation par un quaternion d'attitude. 

NB2 : Pour une orbite héliosynchrone, il faudrait de plus tenir compte de la rotation de 0.98°/jour du plan de l'orbite, autour de l'axe nord-sud. Dans un premier temps nous n'en tenons pas compte.

3°) EQUATIONS SATELLITE: 

a) Le moment cinétique complet satellite + roue comprend 2 termes:

b) Couples externes appliqués au satellite complet:

Dans notre cas, il n'y a pas de moteurs et donc il n'intervient que : 

NB : Le calcul du couple de commande magnétique, suppose la connaissance à bord des composantes du champ magnétique soit :

-      Sous forme analytique avec utilisation de la position ( donc restitution d'attitude )

-      En utilisant un boîtier de magnétomètres et les moyens de calcul, pour élaborer les composantes du champ magnétique et éventuellement de sa dérivée. 

c) TMC appliqué en axes inertiels, projeté en axes satellite: 

Le lecteur utilisera la dérivation intermédiaire en axes satellite

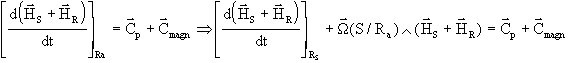
Finalement , sous une forme équivalente on a :

On voit alors apparaître au premier membre l'expression classique du TMC appliqué au satellite et au second membre 2 termes supplémentaires traduisant la présence de la roue en rotation. 

C'est donc cette dernière équation qui sera le socle du SCA, accompagnée de celle du comportement de la roue   

c) Equations en axes satellites,

Ce calcul a déjà été réalisé sur le site, et donne cas général  

SANS ROUE : 

1à Sans roue, mais avec gradient de gravité.:

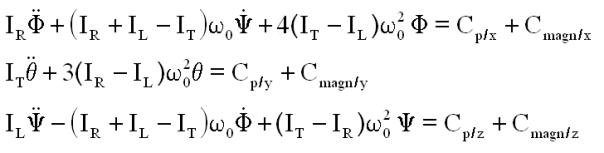
2à Sans roue, sans gradient de gravité  

REMARQUES :

On note que sans couples extérieurs, la stabilité du système n'est acquise  que si :

Les mouvements roulis-lacet sont couplés.Le tangage est découplé du lacet et du roulis.. 

AVEC ROUE  SUR L'AXE TANGAGE:

On note Cr le couple de réaction de la roue sur le satellite et w la rotation relative de la roue par rapport au satellite 

1à Avec roue et gradient de gravité, qui se réduit à sa partie principale avec des axes principaux..

2à Avec roue, sans gradient de gravité.

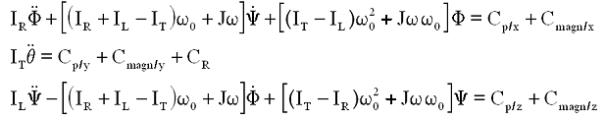
4°) ETUDE PARTICULIERE DES COUPLAGES GYROSCOPIQUES DUS A LA ROUE:   

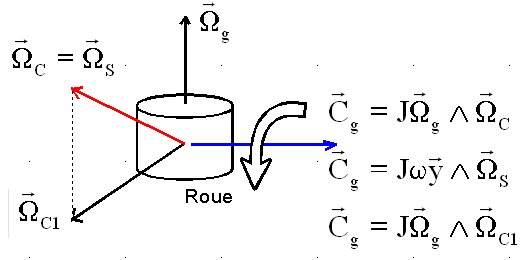
Considérons un  solide appelé "carter" ( içi le satellite ) comporte un gyroscope de moment d'inertie J. ( corps tournant à vitesse angulaire w autour de l'axe y ) 

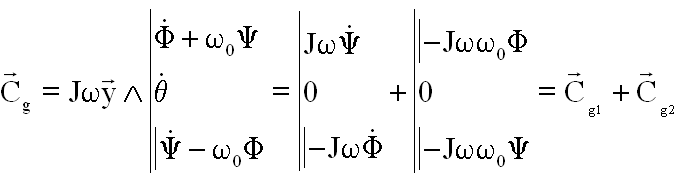
CONCLUSIONS :

La roue apporte 2 effets:

1 - Le couple Cg1 traduit les couplages roue-satellite, ce sont les termes que l'on retrouve devant les dérivées, d'ailleurs avec des signes opposés.

des équations en F et Y.

2 - Un couple Cg2 traduit le couplage avec le mouvement orbital, couplage qui entraîne que l'axe de la roue essaye de s'aligner sur l'axe de la rotation orbitale. En clair la rotation w y "veut s'aligner" sur woY.  Avec comme conséquences:

Si   w > 0 l'effet est stabilisant à coup sûr, ce qui se constante sur les termes suivants des équations en F et Y.

Si  w < 0 l'effet est déstabilisant, car la roue tend à se retourner complètement, entraînant le satellite dans cette même opération. Il est probable que les bobines vont travailler plus. L'effet  devrait être d'autant plus gênant que la roue tourne vite, sauf que la roue prendre une rigidité gyroscopique de plus en plus importante. En pratique l'étude réserve des surprises ( sauf erreur de ma part ).

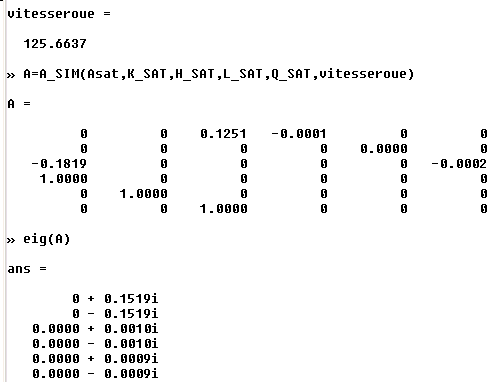
Pour la suite, je préfère revenir à une équation d'état du satellite avec roue et gradient de gravité, de la forme matricielle :

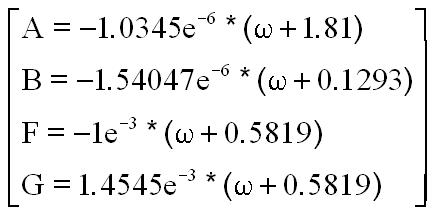
Recherchons les valeurs propres, au nombre de 4 et complexes conjuguées 2 à 2. Comme le système libre est non dissipatif, les parties réelles devraient être nulles. Nous trouverons donc une équation caractéristique bicarrée avec 2 racines négatives, conduisant à deux pulsations propres seulement.

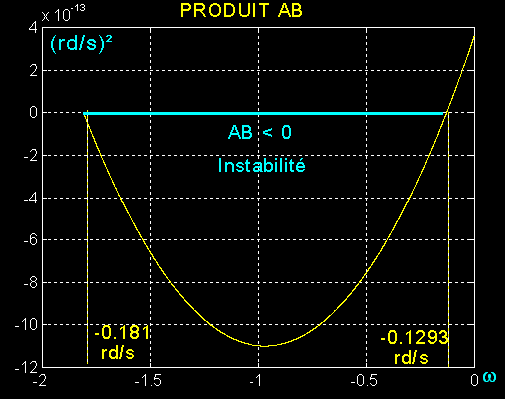
L'équation caractéristique s'écrit :

Le comportement du système dépend de la nature des racines, donc classiquement du produit P et de la somme S

La conclusion est immédiate et inattendue ( sauf erreur de ma part ) le satellite pourrait être instable avec une roue à vitesse réduite négative entre - 0.13 et - 1.81 rd/s. 

Pourquoi? Problème à trancher?

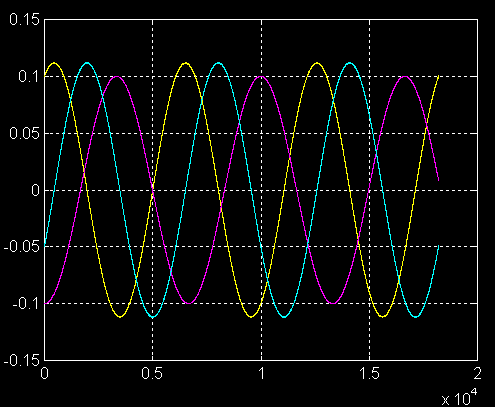
RESULTATS CONFIRMES PAR LA SIMULATION libresat

Récupérer les fichiers

REMARQUE :  la zone est si étroite et la divergence si lente qu'elle ne devrait pas poser de problème lors de sa traversée, sauf dans un seul cas: la panne et le mode survie dans cette zone de vitesse.

RESULTATS DES SIMULATIONS

1°) Autour de la zone instable :

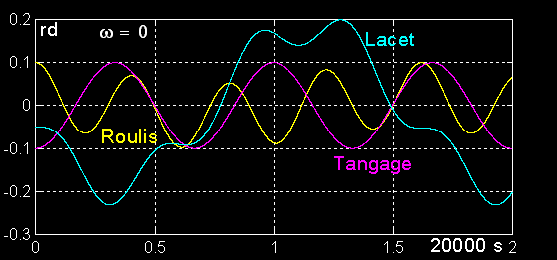
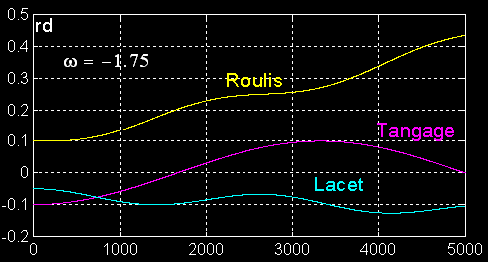
C'est le lacet qui est déstabilisé en premier

C'est le roulis qui est déstabilisé en premier

7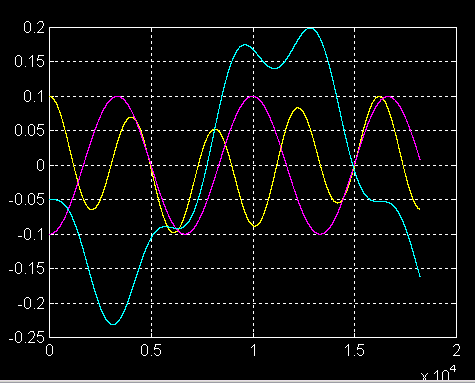

3°) EQUATION ROUE: 

En négligeant, dans le mouvement rapide de la roue, les dérivées premières et secondes des angles satellites ( mouvements lents ) on obtient une équation du mouvement de la roue : 

Ceci nous donne un lien entre le tangage et la roue, en négligeant les perturbations petites au regard du couple roue 

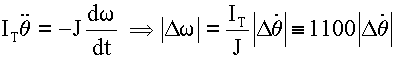
II UNE CHAINE POSSIBLE D'ASSERVISSEMENT DU TANGAGE SEUL : 

A - REMARQUES INITIALES :

-           Sous l'hypothèse d'une matrice d'inertie diagonale, les oscillations libres du tangage sont découplées du roulis-lacet.

-           A l'altitude 817 km et surtout un nanosatellite, le couple du gradient de gravité est très faible, d'ailleurs l'oscillation libre sous gradient est très lente de pulsation et période ( proche des caractéristiques orbitales ) :

-           Le contrôle par roue suppose une surveillance par seuils de détection, donc en général non continue, avec des actions de durée limitées et la mise en jeu d'un couple important ( max 6 10^-3 Nm)devant ceux des perturbations ( max vers 5 10^-7Nm )ou du gradient de gravité ( 1.12 10^-8 Nm).

-           Donc  lors du fonctionnement de la roue, on peut dans un premier temps, pour cerner les principaux paramètres, négliger toutes les actions sauf le couple roue.

-           On appellera q_ref la valeur de référence ou de consigne du tangage, d'abord nulle pour une première étude, mais pas forcément, en présence d'une perturbation qui risque de décaler la valeur stabilisée du tangage.

-           On gardera à l'idée le couple roue max Cmax= 6 10^-3 Nm, et on choisit pour commencer une régulation proportionnelle-dérivée, à partir d'un écart important de 20°.    

B - DONNEES NECESSAIRES :  

Cext couple extérieur comprenant perturbations ( sans gradient de gravité ), et actuateurs internes ( magnétocoupleurs)

NB :On y intégrera donc le couple aérodynamique évalué, sans autre précision, à un maximum de 3.6 10^-8 Nm 

T1 ( par exemple 0.2 s ) retard pur de l'actionneur constitué de la roue 

T2  ( par exemple 0.5 s )  retard pur de la détection de position, K2 gain des détecteurs

B(p) fonction de transfert détection position-vitesse

H(p) fonction de transfert du modèle satellite comprenant le terme du au gradient de gravité

NB : On pourrait choisir H(p )= 28/(p²+W²) = 28/p²  , on notera aussi que la période d'oscillation due au gradient de gravité est du même ordre de grandeur que la période orbitale.

q_ref consigne de référence en tangage 

A(p) la fonction de transfert de la roue de réaction ( exemple pour satellite Demeter ). Essayons d'en  préciser les caractéristiques:

Equation du mouvement :

On ne garde que le couple roue C_R, et on choisit une  régulation proportionnelle-dérivée

Equation de comportement

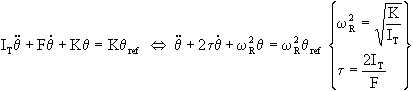
Supposons que pour le dépointage maxi de 20°,  en début de fonctionnement, la roue  délivre 50% du couple max avec le rappel élastique, on a alors  

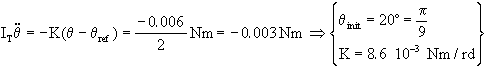
Si on envisage une constante de temps de 1 mn soit t = 60 s, on peut calculer F = 1.2 10^-3 Nms 

Introduction des retards :

On tiendra compte aussi du retard dans la chaîne de mesure de l'angle de tangage ( valeur à préciser , T1=0.1 s choisi pour l'instant ) et du retard dans la restitution d'attitude ( valeur à préciser , T2 = 0.5 s choisi pour l'instant ) 

Introduction du temps de réponse de la roue : 

On adopte ( à défaut d'autre information ) un modèle de roue du premier ordre avec la constante de temps T3 = 0.5 s ( à préciser avec la documentation ) 

La commande sera donc de la forme  

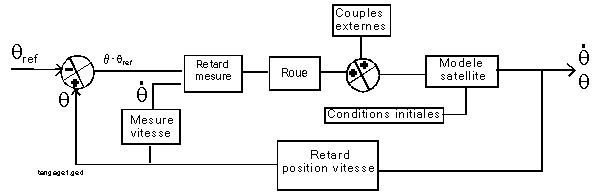
NB1 : Il faudra aussi mettre en place :

1 - Une coupure d'asservissement pour | q - qref  |< D ( à préciser )

2 - Un limiteur de couple roue afin de ne pas dépasser le couple maximum

3 - Un module d'évolution de la vitesse w de la roue, en parallèle avec le simulateur ci-dessus

4 - Une simulation avec la matrice d'inertie réelle pour "voir" l'influence des produits d'inertie qui doivent coupler les 3 mouvements. 

*******************************  Fin de page  *********************************