POSITIONS D'EQUILIBRE EN REPERE ORBITAL
Le système différentiel est établi dans simulation_matrice_quelconque.m et fourni ci-dessous. Nous supposons que seul le gradient de gravité est actif sous sa forme la plus complète et que la roue est à vitesse constante w.
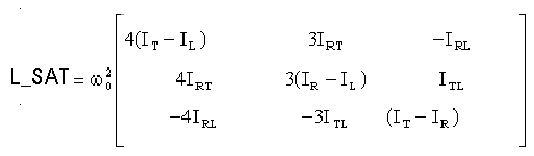
La
présence de termes constants au second membre, indique qu'une position d'équilibre
où les angles sont nuls, est impossible. Ceci à cause des produits d'inertie.
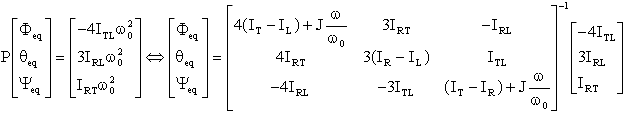
De
plus la position d'équilibre dépend fortement de
la vitesse w
de la roue, qui peut varier de 0 à 6000 t/mn soit de 0 à 628 rd/s

On a en exécutant la fonction equilibr.m , exécuter avant scadesat.m pour initialiser les variables
y=equilibr(vit_roue,vitesse_rotation,Asat,L_SAT,Q_SAT); ==> roulis=0.0004 rd, tangage=0.03 rd et lace t= -1.5 e-9 rd, donc des angles nuls ou presque sauf tangage de 1 à 2°.
Sans roue, la position est très différente : roulis = 0.1395 rd soit 8°,
tangage =1°,2 et lacet = 3°,7 . ce ne sont pas des valeurs anodines et il
faudra peut-être compter avec elles pour choisir au mieux les valeurs de consigne, pour
éviter que la roue ne fonctionne pas trop en continu.
NB : Dans le cas ou IRT , IRL sont nuls, qui est celui préconisé pour les simulations, l'équilibre est :


avec pour la roue arrêtée un angle de roulis important.
La vitesse de la roue augmentant la position d'équilibre se rapproche de ( 0 0 0 )