|
RÉSULTATS COMMENTÉS ET VÉRIFIES DE LA MISE EN SURVIE QUASI INERTIELLE |
![]()
![]()
Voir aussi une étude récente du calcul littéral des éclipses, des durées d'éclipses,
de la puissance solaire reçue et de l'optimisation de puissance, pour les orbites héliosynchrones.
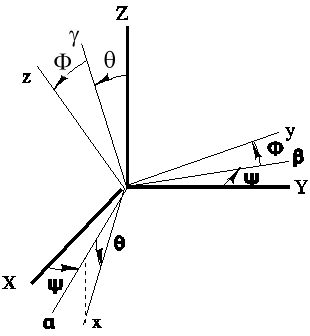
I RAPPELS :
Le nanosatellite est en configuration de travail, stabilisé sous régulation fine.
- Pointage nadir, axe z vers le sol, axe y à l'opposé du moment cinétique orbital porté par Y
- Angles de dépointage très faibles, inférieurs à 5°
- Rotation satellite quasi nulle, quasiment identique à la rotation orbitale à 0.001 rd/s
- Avec ou sans roue à vitesse roue variable ou constante. Si la régulation est celle de Laurens, en pointage nadir, la vitesse roue est constante et négative
Un incident sérieux se produit le jour de numéro J de l'année. Le satellite doit être mis dans un mode de fonctionnement de survie, demandant le moins de consommation électrique possible et une recharge maximum des batteries par les panneaux solaires.
Les techniques possibles de changement d'attitude, parmi celles déjà étudiées sont:
- La mise en spin autour de l'axe de tangage y normal au plan orbital. ( Voir théorie ) production d'énergie du jour 181 ==> 7.37 Watts de moyenne
- La mise en spin autour de l'unitaire soleil ( Voir la théorie ) production minimale d'énergie du jour 181 ==> 9.2 Watts de moyenne
- La précession vers le soleil en période d'éclipse alternant avec une mise en spin ( Voir théorie ) production d'énergie du jour 181 ==> 9.39 Watts de moyenne
NB : à priori la mise en spin autour de la normale aux panneaux, orientée vers le soleil, est impossible à stabiliser.

L'idée nouvelle, vue la configuration particulière des panneaux ( dessin ci-dessous ) est d'essayer ( Voir la théorie ):
- De garder la roue à vitesse constante autour de y = -Y, ce qui permet de faire pivoter le satellite autour de y = -Y, sans réaction gyroscopique et sans couple perturbateur, à condition que le moment cinétique de la roue soit de même sens que le moment cinétique orbital ( négatif pour un pointage nadir ).
- De faire pivoter le satellite autour de son axe y, d'un angle b, de telle manière que l'angle entre la normale aux panneaux et l'unitaire soleil soit minimum. Cet angle b optimal, appelé beta_fix, dépend évidemment du jour de l'année J. Cette contrainte, réalisée, entraîne une attitude fixe par rapport au plan orbital. Nous dirons que c'est une attitude quasi inertielle, vue la rotation à 1°/jour du plan orbital de l'orbite héliosynchrone. Ci dessous b < 0. La simulation présentée ensuite sera réalisée avec b = 305° ou b = -55° ( mesuré autour de y = -Y ) optimum du jour 181 de l'année.

- En arrière plan de la stabilisation, il y a l'idée que le couplage roue-rotation orbitale, va créer, dès que le plan (x,y) s'écarte du plan orbital, une nutation parasite, rapidement amortie par la régulation, permettant au satellite de revenir vers son orientation optimale par rapport au soleil.
II RÉGULATION DE LAURENS :
Rappelons que la régulation de Laurens définit un repère de consigne XcYcZc que le satellite doit rejoindre en faisant en sorte que le champ magnétique B vu du satellite, rejoigne le champ magnétique Bc de consigne vu du repère XcYcZc.
La loi de Laurens est toujours une loi proportionnelle dérivée à 3 magnétocoupleurs et ici, une roue pour assurer le pointage, roue à vitesse constante négative.
III RÉSULTATS COMMENTÉS ET RECOUPÉS AVEC DES CALCULS MANUELS :
Mise en survie, le jour = 181 de l'année, soit près du solstice d'été ( cas le plus défavorable pour l'énergie )
La simulation démarre à partir d'un pointage de travail nadir, à vitesses et angles faibles:
v_roulis0=0.001 rd/s, v_tangage0=-0.001 rd/s, v_lacet0=0.002 rd/s, rouli0=180+0.05 rd, tangage0=-0.02 rd, lacet0=0.001 rd.
La simulation dure 14074 secondes, valeur choisie pour que la mesure de la puissance permanente puisse se faire entre 8000 s et 14074 s exactement une période orbitale de 6074 s.
1°) Vitesses angulaires :
En moins de 5000 secondes, l'opération est terminée, les vitesses angulaires p, q, r en axes satellite sont pratiquement nulles, les valeurs finales sont
p(length(p)) = -9.0970e-008 rd/s q(length(q)) = 2.1625e-005 rd/s r(length(r)) = -9.3946e-006 rd/s ;
Vérification 1 : Le graphe qui suit, montre bien que le satellite reste d'orientation fixe dans le plan orbital, puisque sa rotation vue du repère orbital est l'opposée de la rotation orbitale de 0.001 rd/s. Les autres vitesses sont très faibles.
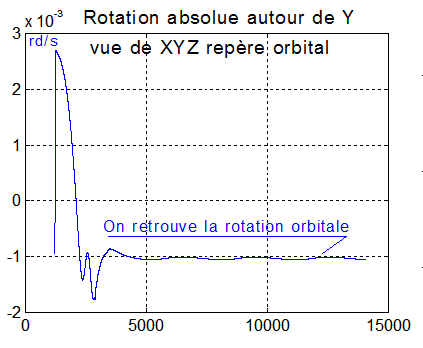

2°) Angles de Cardan :
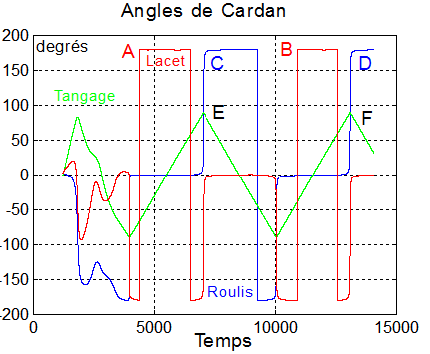
Le graphe des 3 angles paraît un peu compliqué, ceci est dû aux inversions des lignes trigonométriques et à mon choix du repère orbital XYZ, cependant
Vérification 2: Il est clair que le tangage varie linéairement, ce qui est normal, puisque le satellite est inertiellement fixe et c'est le repère orbital XYZ qui tourne à la vitesse angulaire orbitale constante. Donc l'angle est linéaire par morceaux et périodique ( temps entre E et F ) de période 6074 s.
Vérification 3: Les angles de roulis et lacet ne prennent pas de valeurs intermédiaires, c'est 0, 180°, -180°. Preuve que le plan satellite (x z ) reste en coïncidence avec le plan orbital. On voit un échange roulis_lacet répétitif ( la somme des 2 vaut toujours 180° ou -180° ) Cette singularité tient aux angles, dont on sait qu'ils posent des problèmes géométriques de définition lorsque q vaut 90° ou -90°. C'est exactement ce que montre la simulation, les sauts ont lieu en synchronisme en E, F et entre les deux.
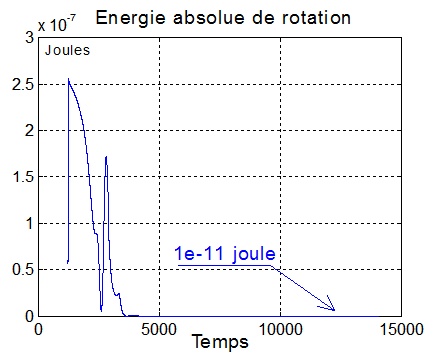
3°) Énergie :
L'énergie absolue est nulle, avec une précision extrême ==> energie(length(temps)) = 1.0201 e-011 Joule
4°) La régulation : Celle de Laurens
Elle est, rappelons le, du type proportionnel dérivée sur la différence entre le champ de consigne et le champ réel. ( Voir la théorie )
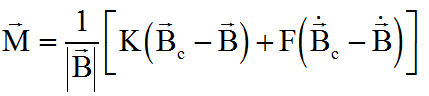
K = 1.6 e-5 SI F = 8.4 e-3 SI
Il est donc tout à fait normal, qu'en fin de régulation Bc-B s'annule. max(norm_PB_moins_B(11000:12000)) = 5.4347 e-007 teslas
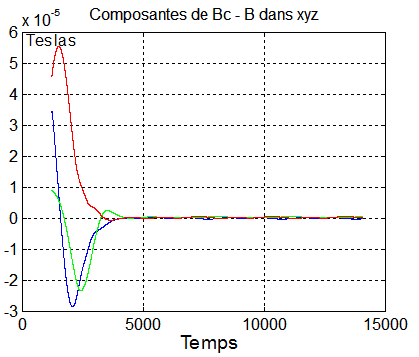
5°) Production d'énergie :
La simulation est prévue pour mesurer puissance et énergie, après acquisition de la bonne attitude, c'est le cas de 8000 à 14074 secondes, très précisément sur une période de 6074 s. On y constate :
- Une excellente puissance moyenne de 11 W jamais atteinte avec les méthodes de survie précédemment étudiées.
Vérification 4: D'abord, l'allure parfaitement linéaire des 2 tronçons, indique une puissance constante, qui confirme que l'attitude du satellite par rapport au soleil est immuable ( stabilisation inertielle )
Vérification 5 : Il n'y a qu'une seule éclipse par période. Nous pouvons la retrouver avec la fonction Teclipse.m, pour le jour 181 de l'année
Teclipse(181) = 1.9528e+003 ==> 1953 secondes
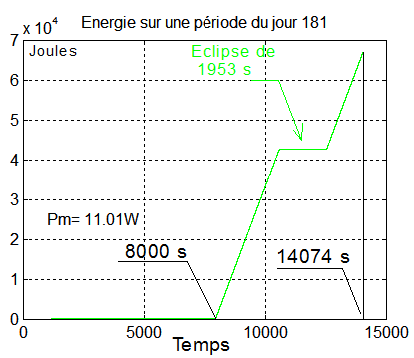
Vérification 6 : La courbe de puissance donne approximativement 16 W constants, ce qui permet de calculer l'énergie reçue sur une période avec éclipse:
puissance_inst(length(q)) = 16.1621
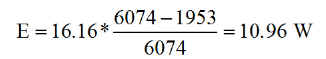

On retrouve donc les 11 Watts annoncés et calculés.
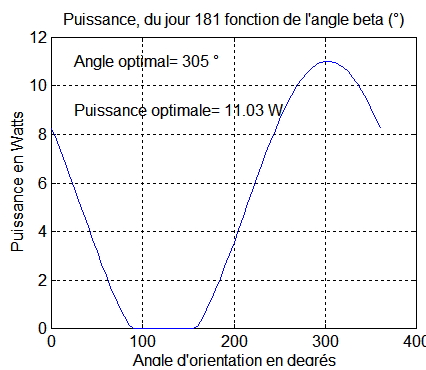
Vérification 7 : Le graphe ci-dessous, indépendant de la simulation, donne pour un jour 181, et un angle b variable de l'orientation satellite, la puissance espérée.
Le maximum est bien de 11 Watts correspondant à une orientation b = 305°. Si on regarde la valeur injectée en début de simulation, on a bien sûr
beta_fix*180/pi = 303°
6°) A propos du quaternion d'attitude : Q = [q1 q2 q3 q4]

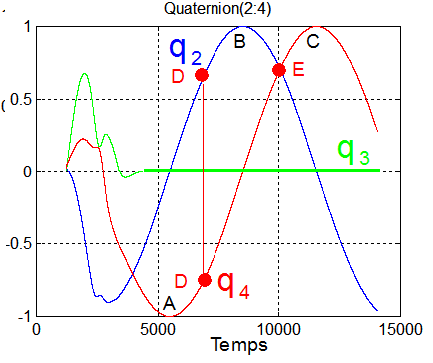
a) Départ : La simulation commence à instant_injection = 1213 s, lorsque le satellite est largué à la latitude de 70° ( exemple choisi ). Les 2 graphes montrent que le quaternion initial est Q =[ 1 0 0 0] donc le quaternion unité, entraînant le repère xyz confondu avec XYZ. Rassurant.
b) Fin de simulation : La première composante est rapidement strictement nulle indiquant que l'angle a de la rotation qui fait passer de XYZ à xyz satellite vaut 180°. Donc le vecteur R axe de la rotation a une composante nulle sur y. R = [ R1 0 R3] sur XYZ

Vérification 8 : Tout repose sur ce vecteur R porteur d'une rotation angulaire d'angle 180°. Donc une symétrie axiale autour R situé dans le plan (x,z), car la deuxième composante est nulle. Les évolutions de q2 et q4, d'allures sinusoïdales, de période double de la période orbitale avec un déphasage de quadrature de 90°, laissent supposer que leur écriture est de la forme ( ce qui sera validé par un calcul manuel indépendant de la simulation ):
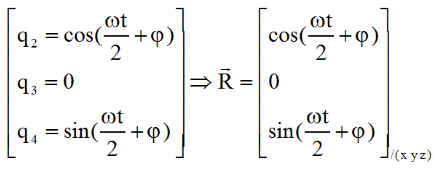
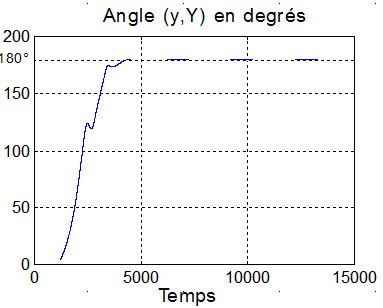
7°) A propos des angles de dépointage : Pour les angles des axes x et X ou z et Z, comme le satellite reste inertiellement fixe, X et Z font donc un tour complet ou 2 demi-tours, linéairement, à la vitesse angulaire orbitale w=0.001 rd/s. Donc, variation périodique de période T = 6074 s, celle du satellite. Les 2 angles sont déphasés de 90°, comme leur disposition géométrique sur le satellite et le plan orbital.
 |
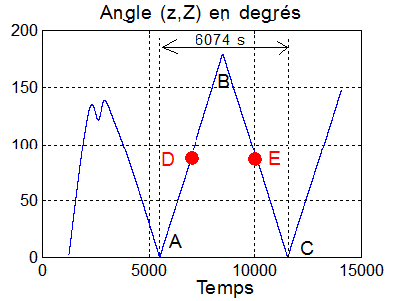 |
Quand à l'angle entre y et Y, que l'on trouve égal à180°, il confirme que le satellite a bien son axe y de sens contraire à Y .De plus, la vitesse de la roue est négative sur y, son moment cinétique est donc parallèle à celui du mouvement orbital, ce qui sécurise l'attitude ( pas de réaction gyroscopique.
8°) A propos du quaternion
Vérification 9 : Le dessin qui suit met en coïncidence les points A B D E sur l'orbite et les points de même nom sur les courbes. La correspondance est parfaite pour tous les points particuliers. Dans tous les cas, le quaternion de passage de XYZ à xyz se réduit à une rotation d'angle 180° ( nous aurions tout aussi bien prendre -180° , mais gardons +180°) autour d'un axe D bien identifié ( qui pourrait être -D ), toujours situé dans le plan orbital. Ci dessous le résumé des axes du quaternion en adéquation avec le quaternion issu de la simulation, que le lecteur calculera avec les courbes.
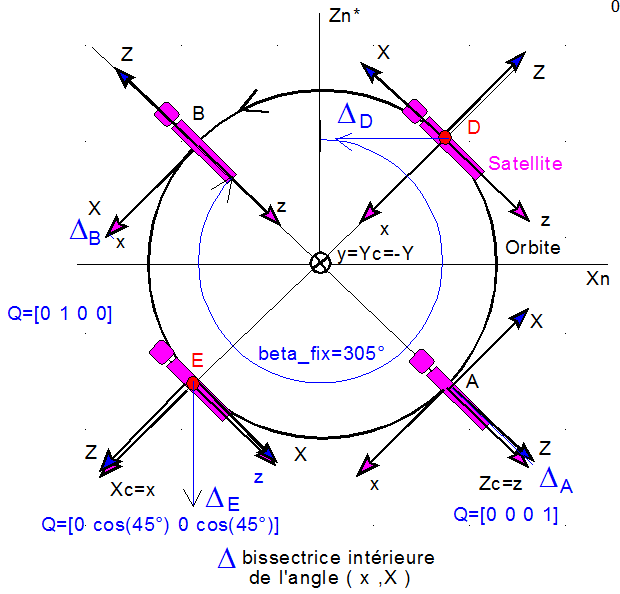
Vérification 10 : Reste à voir la transformation pour un point courant de l'orbite. Ci dessous, toujours avec une rotation de 180° autour de l'axe R = D, bissectrice intérieure des axes x et X.
Un calcul géométrique indépendant de la simulation donne l'angle a, sachant que la position satellite est repérée à partir du nœud, avec convention de t=0 au survol de l'équateur. Un peu de géométrie dans le triangle conduit aisément à la figure et au quaternion du cas particulier. Rappelons que cette figure est celle du cas particulier du jour 181 ou b = 305° q = 145°

Le lecteur établira la relation ( ici particulière ) qui suit, que nous retrouverons plus loin générale, par une autre méthode
|
|

Commentaires: On retrouve bien les expressions sinusoïdales que le graphique avait permis d'anticiper. Bien évidemment, les premiers instants ne coïncident pas, mais en fin de régulation l'accord est parfait, il ne peut pas en être autrement en régime stabilisé..
Vérification 11 : Le tracé des courbes séparément de la simulation donne une excellente similitude
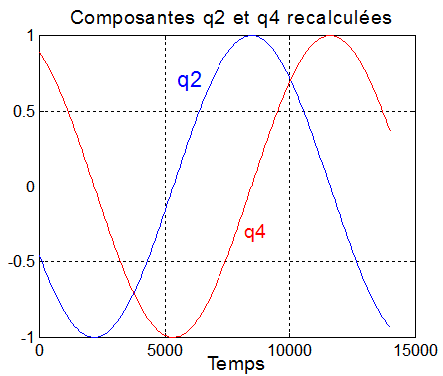
extraordinairement confirmée par le tracé des courbes calculées et simulées, superposées. Qu'espérer de plus pour valider le concept et la simulation !!!.

CAS GÉNÉRAL :
Le lecteur pourra établir qu'exprimé, dans le cas général, avec l'angle b optimal ( c'était 305 ° pour l'exemple, au dessus), le quaternion final vaut:
|
|
NB : Cette formule explique la valeur de a pour le cas du jour 181 où b = 305°.
En effet, a = 90°- wt - 305° (mod 360 ) = 90°- wt - 305° +360°(mod 360 ) = 145°- wt (mod 360 )
9°) Magnétocoupleurs et roue :
a) Magnétocoupleurs : Le graphe montre qu'en régime de croisière, les magnétocoupleurs sont très économes, aucun moment magnétique ne dépassant 0.01 A-m2. Durant l'alignement même, la saturation n'est pratiquement pas atteinte, prouvant que les gains K et F de la régulation sont corrects
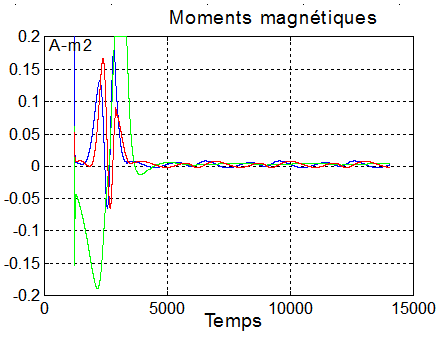
b) Roue : La roue travaille à vitesse constante, son seul rôle, amener grâce à son moment cinétique H = - 3.2e-3 mN une stabilisation gyroscopique, puisque ce moment cinétique est colinéaire à celui du mouvement orbital. Seul H est important, le choix de la roue est donc facile.

9°) Production d'énergie :
Le graphe ci dessous confirme qu'une fois stabilisée, l'attitude des panneaux par par rapport au soleil est figée à 25° pour le cas étudié du jour 181. Ceci garantit une puissance constante. Compte tenu du temps d'éclipse de 1953 secondes, on retrouve bien les 11 watts annoncés. On aura noté que la survie est atteinte en 4000 secondes, c'est à dire moins d'une période.
P = 18*cos(25*pi/180)*(6074-1953)/6074=11.06 W

10°) Synthèse et enchaînement des simulations : pour montrer la facilité des manoeuvres.
Simulation survfix3.m initialisée par beta_dat.m ( retrouver les fichiers dans surfix1.zip )
Le graphe qui suit résume une séquence complète d'enchaînement des simulations, sur 30000 secondes.
1 - Attitude initiale de pointage nadir: faibles vitesses et angles quasi nuls. De l'injection à 6000 s
2 - Première mise en survie, réalisée à 6000 s, prolongée jusqu'à 11000 s
3 - Déclenchement du retour en pointage nadir à 11000s , réalisé en 1000 s et conservé jusqu'à 170000 s
4 - Retour en mode survie à 17000 s en 1500 s durant jusqu'à 23000 s
5 - Déclenchement du retour en pointage nadir à 23000s , jusqu'à 28000 s

Commentaire :
Le basculement d'un mode à l'autre est aisé et rapide. En pratique, la roue tournant toujours dans le même sens que celui du mouvement orbital, sécurise totalement les opérations.
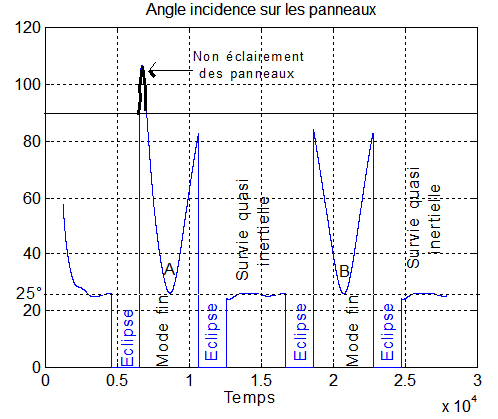
Le résultat qui suit résume à lui tout seul la situation en ce qui concerne l'énergie. Le mode survie est à puissance constante en période d'éclairement (16 Watts garantis pour 11 Watts réels compte tenu de l'éclipse), alors que le mode pointage nadir, peut conduire, en plus des éclipses à un non éclairement des panneaux, mal orientés par rapport au soleil, à un certain moment. On constate cependant que le mode fin passe bien, une fois par orbite dans l'orientation optimale donnant la puissance de 16 Watts.

Le graphe de l'angle d'incidence des rayons sur les panneaux montre bien aussi la différence entre le mode fin pointage nadir et le mode survie. Dans le premier, l'angle est variable pouvant même conduire à un non éclairement, alors que le second montre un angle optimal, constant de 25° environ, assurant, compte tenu des périodes d'éclipse ( 1953 s pour le jour 181, sur la période de 6074 s ) une puissance de 11 Watts. On observe aussi qu'à chaque orbite le satellite passe une seule fois ( A ou B ) dans sa position d'énergie maximale où l'incidence des rayons solaires est alors optimale de 25°
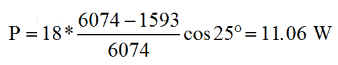
L'évolution des vitesses angulaires du satellite relative par rapport au repère orbital, conforte l'analyse des séquences et montre que seule la vitesse de tangage est sollicitée ( -0.057 °/s équivalent à -0.001 rd/s vitesse angulaire orbitale ), le signe - révèle que y est aligné sur -Y..
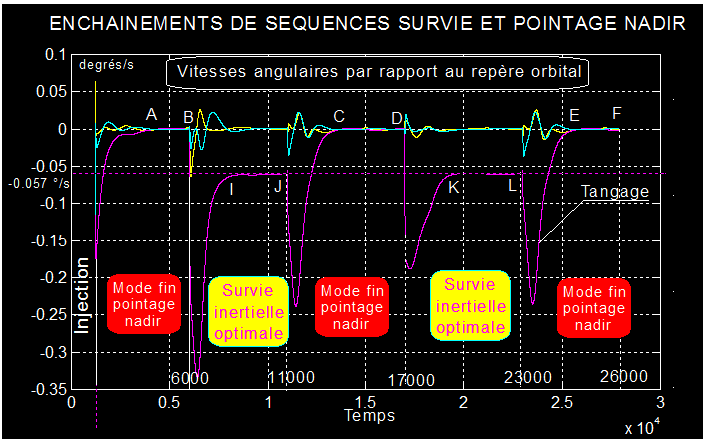
Commentaires :
1 - En mode fin établi (régions AB, CD, EF), Toutes les vitesses angulaires sont nulles confirmant la fixité de xyz dans XYZ
2 - En mode survie quasi inertielle établie ( régions IJ, KL), la vitesse angulaire en tangage est strictement opposée à la rotation orbitale, entraînant une fixité inertielle. Car : - 0.057 °/s = - 0.001 rd/s vitesse angulaire orbitale.
3 - Le basculement d'un mode vers l'autre s'opère en moins de 2000 secondes.
Pour compléter le tableau des confirmations d'exactitude de la simulation: ci-dessous les vitesses angulaires mesurées dans le repère orbital. On voit clairement qu'en survie quasi inertielle la rotation du satellite est exactement opposée à la rotation orbitale w = 0.001 rd/s autour de Y. Ceci pour obtenir une rotation inertielle nulle autour du tangage. Les autres rotations de roulis ou de lacet restent toujours nulles dans les portions stabilisées.

III OPTIMISATION SUPPLÉMENTAIRE DES TEMPS DE BASCULEMENT DE MODES :
Le graphe donnant les quaternions calculés et simulés montre que les composantes q2 et q4, lors des basculements de mode, viennent rattraper rapidement et fidèlement les composantes calculées. Ceci suggère de mieux choisir l'instant du basculement, pour réduire au minimum la phase transitoire de rattrapage. C'est l'objet de la simulation.
surfix4.m initialisée par beta_3dat.m
( Retrouver les fichiers avec surfix1.zip )
Idée : Tout le long de la trajectoire, la rotation continue du mode survie se fait toujours suivant l'une des bissectrices des angles entre les vecteurs x et X. Le basculement de mode correspond en mode fin, à une rotation d'angle 180° ou -180° autour de x ou d'ailleurs -x, lorsque xyz est confondu avec XYZ. Donc l'instant optimum à saisir est celui où x et X sont confondus ou opposés, dans les 2 modes.
CALCULS DES TEMPS DE BASCULEMENT IDÉAUX :

Cette situation se produit lorsque a vaut 0 ou 360°, c'est à dire 2 fois par période lorsque q2 = 1 ou -1 puisque a/2 = 0 ou 180° ==> a = 0 ( mod 360° )
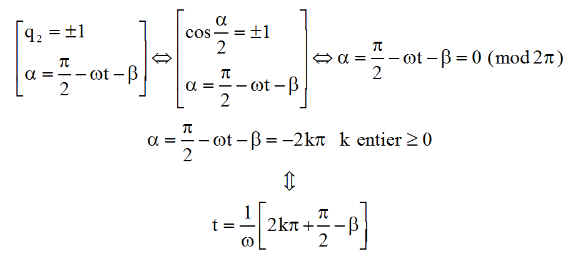
Le calcul des 5 premiers temps donne ( avec 1/w = 966.668, b = 305°*pi/180 pour le jour J=181 de l'année )
| k ==> | 1 | 2 | 3 | 4 | 5 |
| t | 2480 s | 8554 s | 145628 s | 207029 s |
26776 s |
Ci dessous pour T1=14600 s et T2=26740 entre les 2, 12140 s soit le double de la période orbitale.
Exemple 1 : Les temps de basculement sont: 6000 s non optimisé, 11000 s non optimisé, 14600 s optimisé et 26740 s optimisé. La transition en 14600 et 26740 s sont parfaites
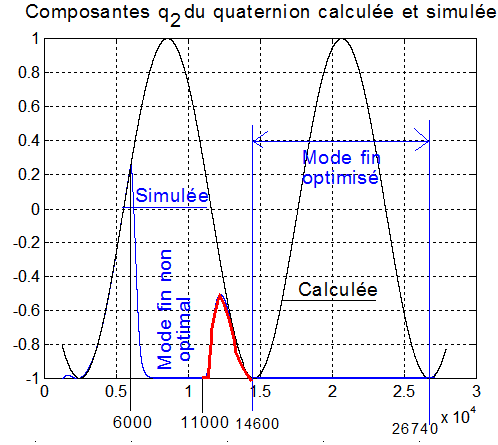
Exemple 2 : Les 2 premiers temps ont été légèrement modifiés 4000 et 10000 s au lieu de 6000 et 11000 s.
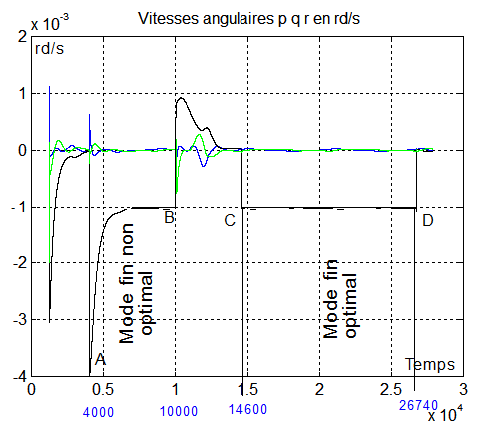

Commentaires :
On pourra apprécier la rapidité et l'élégance des basculements optimisées en B C et D alors qu'en A il ne l'est pas.
Cette différence de basculement s'observe ainsi:
- le premier débute et termine à 2 instants aléatoires, le second commence et finit à 2 instants optimisés 14300 et 26740 s.
- La transition du quaternion se fait dans la continuité de la composante et apparemment de sa dérivée aussi.
CONCLUSION SUR LE CALCUL DES TEMPS :
En opération, sur orbite, il est impensable de repérer les instants à partir de la date de lancement. Il est préférable de noter à chaque orbite l'heure Tn de survol de l'équateur au nœud ascendant et de donner l'instant optimal de basculement, pour l'orbite courante qui commence à partir de cette référence:
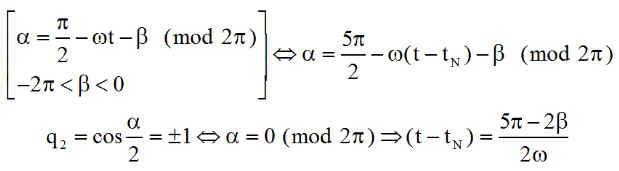
|
|
Exemple pour jour=181, b = 303°==> t = 2480 s les instants suivants se décalent de proche en proche de la période orbitale T = 6074 s
IV ROBUSTESSE PAR RAPPORT A UNE ERREUR DE LOCALISATION DU SATELLITE :
La pertinence de la simulation ne fait aucun doute, au vu de l'ensemble des vérifications effectuées. Reste à savoir quel est l'impact, sur la stabilité de l'attitude et sur la récupération d'énergie, face à une erreur de localisation.
Idée :
1 - Garder le calcul du champ magnétique réel, de la position réelle du satellite, comme si les composantes étaient donnée par le magnétomètre 3 axes.
2 - Supposer que l'erreur de localisation, ne concerne que la latitude, puisque les variations infimes du rayon orbital ne comptent pas et que l'inclinaison est parfaitement garantie sur de longues périodes par l'héliosynchronisme, même s'il est un peu affecté par les perturbations.
Ceci signifie que la situation peut être modélisée par un simple décalage du temps, qui sert dans mes simulations à calculer, le champ magnétique orbital, donc:
|
CHAMP MAGNÉTIQUE ORBITAL DÉCALÉ angulairement de Dq ou de manière équivalente de DT en temps orbital Simulation surfix2.m initialisée par beta_dat.m |
Résultat : En faisant tourner plusieurs fois la même simulation :
| Angle ( ° ) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
| Temps ( s ) | 0 | 37.5 | 67.5 | 101.2 | 150 | 187.5 | 202.4 | 240 |
| Puissance( W) | 11.01 | 10.99 | 10.94 | 10.87 | 10.77 | 10.65 | 10.5 | 10.33 |
| Angle ( y,Y ) ° | 179.5-180° | 179.5-180 | 179.5-180 | 179.2-180 | 179-180 | 178.7-180 | 178.5-180 | 178.4 |
Au dessus de 4°, on observe une oscillation de la vitesse de tangage de 20% de part et d'autre de la vitesse orbitale.
Les moments magnétiques de commande restent inchangés, moins de 0.02 A-m2
Le dépointage de z par rapport à Z reste inférieur à 2°, donc tout à fait acceptable au regard des spécifications.
Quant à l'énergie, la perte de 0.7 Watt est modeste. Une production de 10 Watts en continu est donc garantie.
IV UNE SEULE RÉGULATION DE LA MISE EN ORBITE AU MODE FIN OU A LA SURVIE :
Simulation synthese.m initialisée par betaSdat.m
( retrouver les fichiers avec surfix1.zip )
Cette simulation, basée sur la seule régulation de M Laurens, regroupe tous les cas de figure:
1 - Injection à 1213 s
2 - Réduction des vitesses angulaires importantes en "détumbling" de 1243 s vers 4000 s
3 - Acquisition du pointage Nadir, conservé jusqu'à 10000 s
4 - Basculement non optimisé, sur le mode survie du jour 181, à 10000s jusqu'à 14594 s
5- De 14594 s à 20668, passage en mode fin
6 - 0 20668 s basculement en mode survie, jusqu'à 26741 s
7 - Nouveau basculement en mode fin jusqu'à la fin de la simulation.

Le comportement des vitesses angulaires pour t=10000 s, temps choisi aléatoirement, alors que les autres basculements sont calculés à des instants bien choisis où la composante q2 vaut 1 ou -1, prouve que l'optimisation du choix est importante ( Voir l'aspect théorique plus haut )
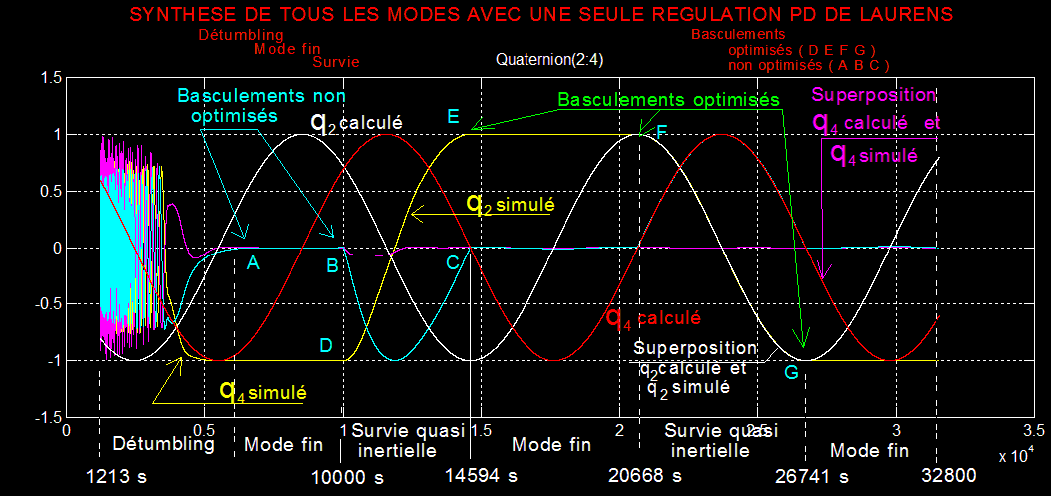
La remarque précédente est confortée par le graphique ci-dessus où la transition entre les modes est de classe C1 en D E F ou G et brutale en B.
On notera que lorsque la régulation en survie quasi inertielle est stabilisée ( par exemple entre les points F et G ) la coïncidence du quaternion q2 calculé et q2 simulé est parfaite, élément révélateur de la qualité de l'intégration numérique et de la pertinence de la régulation.
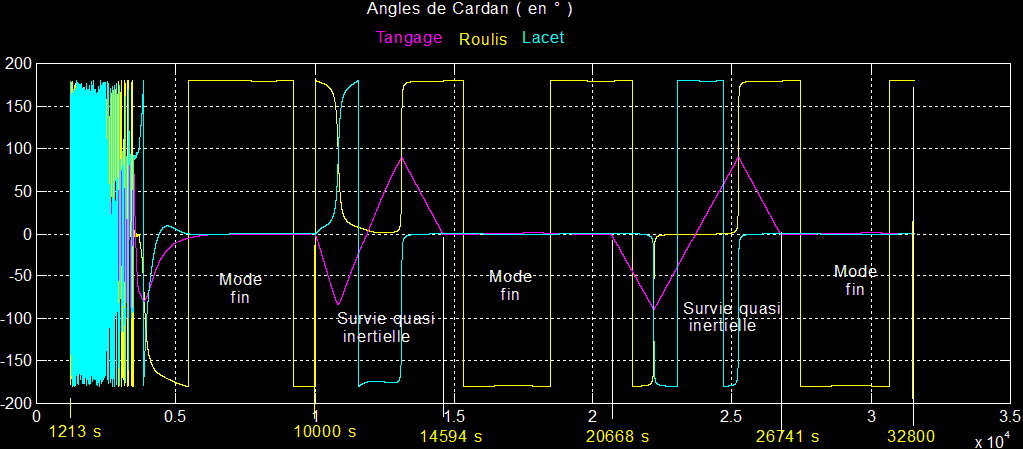
Très clair, le graphe des angles de Cardan montre bien le roulis à 180°, assurant le pointage Nadir, avec un tangage linéaire par morceaux, lors des mises en survie quasi inertielle. Normal, car le satellite est inertiellement fixe alors que le repère orbital tourne à la vitesse angulaire orbitale de l'ordre de 0.001 rd/s
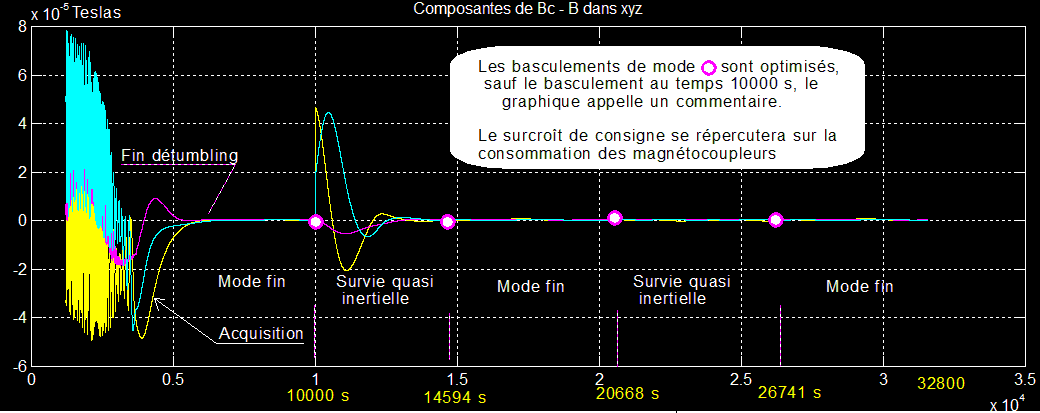
Nouvelle illustration de l'intérêt d'optimiser le choix des temps de basculement. L'écart à la consigne Bc-B varie brutalement lors d'un choix non optimisé.

Les 2 graphes au dessus et au dessous, doivent être mis en correspondance, car incidence des rayons solaires et puissance sont intimement liés. On peut y voir :
1 - Les positions et durée d'éclipse ( 5 pour 5 orbites environ )
2 - Pour le mode fin, les points B C D sont les points d'incidence minimale atteints une seule fois par orbite et situés sur des points de basculement optimaux, alors qu'en A passe les panneaux passent par l'incidence optimale en cours d'orbite.
3 - La puissance maximale possible est de 16 Watts en éclairement, hors ellipse. Elle correspond à une incidence minimale de 25°.
4 - Cette puissance maximale est continue et constante dans le mode survie quasi inertielle, alors qu'elle ne l'est pas du tout en mode fin, variant de 3 à 16 watts, sur l'orbite.

V UNE SEULE ET DERNIÈRE RÉGULATION DE LA MISE EN ORBITE AU MODE FIN OU A LA SURVIE :
Simulation synthesT.m initialisée par betaSdat.m
( retrouver les fichiers avec surfix1.zip )
Cette simulation, basée sur la seule régulation de M Laurens, regroupe tous les cas de figure:
1 - Injection à 1213 s
2 - a) Réduction des vitesses angulaires importantes en "détumbling" de 1243 s vers 4000 s
b) Lancement de la roue dès l'injection ( où elle est arrêtée ) , pendant 2000 s, sous un couple constant de 1.6 e-6 Nm soit 40% du couple max de la roue
3 - Acquisition du pointage Nadir, conservé jusqu'à 10000 s
4 - Basculement non optimisé, sur le mode survie du jour 181, à 10000s jusqu'à 14594 s
5- De 14594 s à 20668, passage en mode fin, après basculement optimisé
6 - A 20668 s basculement optimisé en mode survie, jusqu'à 26741 s
7 - Nouveau basculement en mode fin jusqu'à la fin de la simulation.
Conclusion :
Comme prévu, la mise en route de la roue de la vitesse nulle, jusqu'à 100 rd/s ( 955 tours/mn ) est sans dommage pour le détumbling qui amortit les effets indésirables. Tous les résultats sont identiques au cas précédent où la roue était supposée tourner à 100 rd/s dès le départ.
On ne donne donc qu'un seul graphique de synthèse.
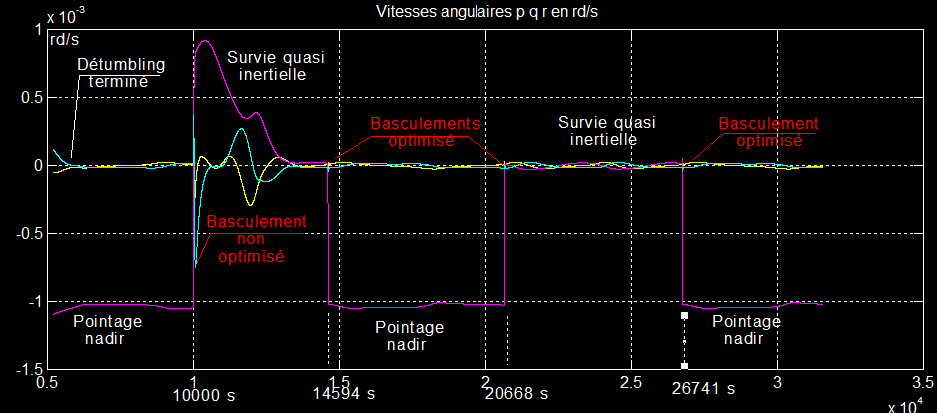

Comportement de la roue
*************** Fin *************
Février 2016, revu avril 2016, revu février 2017