 |
|
UTILISATION ÉVENTUELLE DES PANNEAUX SOLAIRES ET DES ÉCLIPSES POUR UNE LOCALISATION SOMMAIRE |
Étude détaillée des conditions d'éclipse, y compris avec réfraction atmosphérique
Orientation et repère de consigne pour une survie optimale quasi inertielle.
Choix d'une stratégie de survie quasi optimale et totalement inertielle
********************
Cette page, pour examiner la possibilité de localiser approximativement, en mode nominal, un nanosatellite non équipé d'une restitution d'orbite, grâce à la mesure de la puissance du générateur solaire ou à l'aide de la détection des transitions d'entrée et ( ou ) de sortie d'une éclipse. L'orbite concernée est héliosynchrone à 615 km avec une heure locale au nœud ascendant de 20 h 30 ou 22 h 30. Dans un premier temps, l'atmosphère est supposée ne pas dévier les rayons solaires, et dans un second temps on prend en compte la réfraction atmosphérique.
Donnons d'abord l'essentiel des résultats avant de les démontrer:
|
ATTENTION !!! Calculs seulement dédiés aux orbites circulaires héliosynchrones, pour un satellite, de normale N au plan des panneaux solaires dans le plan (Y, Z ) H = Heure locale au nœud ascendant, ang = angle d'inclinaison des panneaux, i inclinaison orbitale héliosynchrone, Po puissance maximum des panneaux d (J) = la déclinaison solaire du jour J , DL = 15(12-H) longitude nodale du soleil en degrés, Z = altitude orbitale, RT = rayon terrestre, T = période orbitale |
|
Constantes A, B, C, a, b, c fonctions de i, d, DL et ang=35° ---------------------------------------------------
|
|
Notations : q, q1, q2 angles polaires du point courant, du point de sortie de l'éclipse ( temps t1 ) et du point d'entrée en éclipse ( temps t2 ), mesures depuis le survol du nœud ascendant
|
|
Résultats relatifs à l'éclipse,
Puissance instantanée P(q) et puissance moyenne Pm
ou encore montrant le rôle de ang = 35°
|
|
Date DN de survol du nœud ascendant déduite des transitions DT1 date satellite de la transition de puissance en sortie d'éclipse DT2 date satellite de la transition de puissance en entrée d'éclipse
|
|
Prise en compte de la réfraction des rayons par l'atmosphère
Date DN de survol du nœud ascendant déduite des transitions DT1 date satellite de la transition de puissance en sortie d'éclipse DT2 date satellite de la transition de puissance en entrée d'éclipse
|
|
CALCUL DE PUISSANCE MOYENNE
|
|
MISE EN MODE SURVIE QUASI INERTIELLE
Le mode survie consiste à placer, chaque jour J, dans le plan orbital, le satellite dans une orientation fixe, donnée par l'angle s = (XN,XC) mesuré autour de Yc = -Y
Le vecteur champ magnétique de consigne Bc est en axes satellite
Les instants de déclenchement optimum de la mise en survie sont
|
|
Compromis possible pour une régulation simplifiée [ 0 < jour < 100 et 265 < jour < 365 --> s = 90°] [100 < jour < 265 --> s = 130° ] Puissance minimale moyenne, compte tenu des éclipses, garantie de 12 W avec perte limitée à 0.5 W |
NB : pour l'utilisation de Arctg2 dans les inversions trigonométriques, voir en annexe 0
I EXPRESSION DE LA PUISSANCE INSTANTANÉE :
Le repère orbital classique est X Y Z, avec X suivant la vitesse, Y qui porte le moment cinétique et Z le zénith . On suppose dans toute cette partie qu'une régulation a stabilisé le satellite en position nominale, pour nous en pointage nadir, donc x = X, y = -Y, z = -Z. Ainsi nous considérons que la normale N aux panneaux est dans le plan (Y,Z) du repère orbital. On notera dans le cas général que ang > 0. Pour nous ce sera ang = 35°.
NB : Un peu plus loin, pour 0 < H < 12, il faudra retourner le satellite ou ce ce qui revient au même changer ang en ang = 180°- ang.
1°) Préliminaires :
La normale N aux panneaux a pour composantes dans le repère XYZ ( NB : En supposant une régulation parfaite )
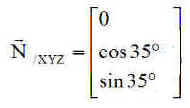
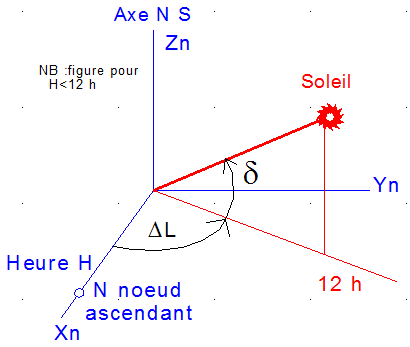
Le décalage angulaire DL du soleil, en longitude, dans le repère Xn Yn Zn associé au nœud ascendant vaut compte tenu de 15°/heure
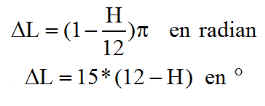
On rappelle une formule simple de Fletcher, donnant la déclinaison, en degrés, du soleil, suivant le jour de l'année( Il en existe bien d'autres, suivant la précision souhaitée )
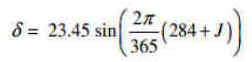
Les composantes de l'unitaire du soleil dans le repère XnYnZn associé au nœud ascendant, sont:
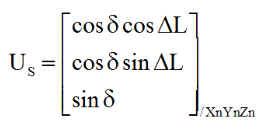
Le passage du repère orbital XYZ au repère nodal XnYnZn utilise la matrice M ( déjà rencontrée ailleurs ), où q = w(t - to) est l'angle polaire mesuré depuis le passage au temps to au nœud ascendant.
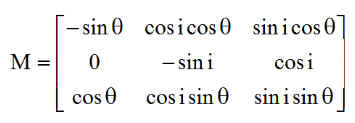
On déduit l'expression des composantes de l'unitaire US du soleil, dans le repère orbital XYZ par US/XYZ = M US/XnYnZn
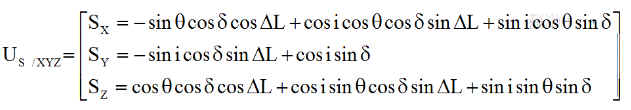
2°) Puissance des panneaux :
Po = 18 W est la puissance nominale des panneaux en éclairement normal au plan des panneaux. N désigne la normale aux panneaux.
Hypothèse importante: On suppose la régulation de Laurens parfaite ( ou tout autre régulation d'ailleurs ) et donc un alignement exact du repère satellite ( x = X, y = -Y, z = -Z ). Hypothèse justifiée, car même pour un dépointage de la normale aux panneaux de 5°, l'erreur relative sur la puissance ne serait que de 0.38 % soit 0.07 Watts sur les 18 W maxi.
La puissance instantanée reçue est
![]()
Nous pouvons écrire cette puissance (compte non tenu des portions sous éclipse ) sous la forme condensée ( le lecteur fera le calcul ):
|
ou encore
|
NB : comme DL = -127°.5 pour H = 20 h 30 ou -157°.5 pour H = 22 h 30, la constante B est toujours < 0 alors que C peut s'annuler, pour une déclinaison de -6°242 correspondant environ aux jours 65 et 300. Ce qui pourrait nous créer de sérieuses difficultés pour inverser la tangente. Attention, il vaut peut être mieux utiliser Arctg2(B,C), pour éviter les singularités de l'inversion de la tangente ( voir annexe 0 ).
Les simulations montrent bien qu'en dehors des éclipses, la loi de puissance est en apparence sinusoïdale par morceaux. Les constantes A, B, C sont parfaitement connues dès que sont données l'inclinaison orbitale, la puissance des panneaux, l'heure locale H au nœud ascendant et le numéro J du jour de l'année qui fixe la déclinaison solaire.
NB : Il n'est pas utile de vérifier que les panneaux sont éclairés du bon coté, car visiblement, pour cette orbite et heure H, la puissance P est toujours positive.
Vérifications : pour une orbite Z = 615 km H = 20 h 30 et J = 270, des panneaux à 35° on a : A = 11.67 B = 6.28 C = 0.65 ce qui donne une puissance fonction de la position sur l'orbite q = wt
|
P = 11.67 -6.28 cosq +0.65 sinq = 11.67+6.29 sin(q-84°09) (1) |
Ainsi la puissance pourrait varier de 5.36 W à 17.98 W le jour 270. C'est bien ce que donne la courbe obtenue par la simulation normale sous régulation de Laurens. Les points en rouges ont ceux calculés avec la relation (1) compte tenu de l'expression de q. On retrouve la valeur moyenne présentée par ailleurs à 11.67 W.
Pour le calcul du temps, la formule ci-dessous le donne, à un nombre entiers de périodes orbitales près. Le graphique qui suit provient d'une simulation et est complétée par les valeurs obtenues avec nos calculs précédents. La correspondance est parfaite, ce qui valide la simulation et nos formules acquises plus haut.
NB : La puissance est mesurée à partir du moment où dans une simulation débutant au moment de l'injection, l'acquisition et la stabilisation sont assurées, ici au temps 4000 secondes, elle se termine exactement après une période de 5820 secondes, donc à 9820 s pour avoir une mesure d'énergie sur une période exacte.
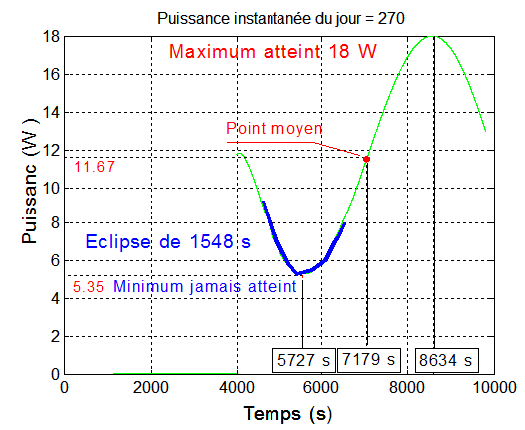
Pour cette configuration la puissance moyenne est de 10.05 W/orbite
3°) Peut-on utiliser la mesure de la puissance pour localiser le satellite? :
Connaissant:
- le jour J
- l'heure locale H au nœud ascendant
- l'inclinaison i du plan orbital sur l'équateur
- L'erreur absolue maximum DP sur la mesure de P
Nous sommes en mesure de calculer les 3 constantes A B C. Donc nous connaissons la loi de la puissance pour la position q, cet angle désignant l'angle polaire mesuré depuis le survol de l'équateur.
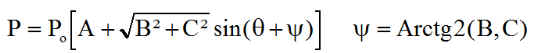
Ainsi si la puissance P est mesurée, en posant K = P/Po, nous pourrions en déduire q.
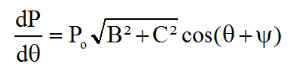
La dérivée de P par rapport à q montre que l'on minimise l'erreur sur q commise sur q lorsque sin(q+y) = 0 donc lorsque P est voisine de sa valeur moyenne A. On peut alors donner une estimation de l'erreur sur l'angle q :
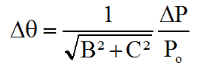
Application numérique : DP = 0.1 W --> Dq = 0.1/6.29 rd = 0.1*180/p/6.29 = 0°.9, nous retiendrons une erreur de l'ordre de 10°/Watt. Tout le problème est donc de connaître la précision de la mesure de P?
Si une erreur sur q de 5° est acceptable, il faut alors une mesure de P à 0.5 W près.
4°) Quelles sont les autres sources d'erreur? :
Nous partons de l'idée que nous ne connaissons pas les données précises de l'injection, qu'il n'y a pas de contrôle ni de restitution d'orbite et qu'il nous faut arriver à localiser au mieux le nanosatellite, avec les "moyens du bord".
Si ce type de localisation, exploitant la puissance où les éclipses, devait être adopté, alors, il faudrait alors étudier finement les diverses sources d'erreur ( en oubliant l'excentricité et l'argument nodal du périgée ):
a) Les dispersions de tir au moment de l'injection, ( position =latitude, longitude, altitude ) et vitesse ( grandeur, pente et azimut ) qui vont jouer :
- sur le demi grand axe a et donc sur la période, effet qui se répercute sur le non respect de l'héliosynchronisme et donc sur une dérive de DL.
- la position initiale sur l'orbite qui décale les dates d'entrée ou de sortie d'éclipse.
- la longitude nodale W qui décale l'heure locale et donc DL
- L'inclinaison orbitale i qui se répercute sur le non respect de l'héliosynchronisme et donc sur DL.
b) Le frottement atmosphérique qui réduit régulièrement le demi grand axe a, avec répercussion sur W et DL
c) L'aplatissement polaire essentiellement décrit par J2 et qui joue sur la dérive des paramètres orbitaux.
Une étude systématique des dérivées partielles des résultats des éclipses deviendraient nécessaires pour évaluer un majorant de l'écart de position et voir s'il est compatible avec la mission.
Peut-être pourrait-on envisager de coupler nos mesures sur les éclipses, avec celles des composantes du champ magnétique moyennant la présence à bord d'un champ de référence embarqué?
II EXPLOITATION POSSIBLE DES ÉCLIPSES :
Nous avons déjà étudié par ailleurs les durées d'éclipses, ce qui a fourni le graphe suivant, par exécution de D:/TIR_2019/energies/t_eclips.m initialisé par energdat.m
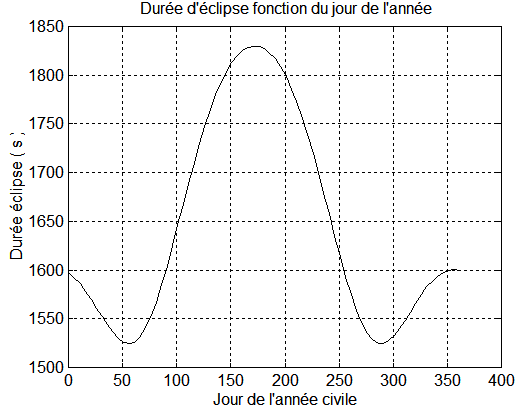
Cas H=20 h 30 Z=615 km i=97°.85
1°) Rappels :
Le satellite est dit en éclipse lorsqu'il se trouve dans le cylindre d'ombre de la terre qui intercepte les rayons solaires. L'entrée et la sortie d'éclipse correspondent à une transition de la puissance des panneaux d'une valeur nettement positive à 0 pour l'entrée et de 0 à une valeur nettement positive pour la sortie. Une telle transition si elle est rapidement détectée pourrait être utilisée pour une localisation du satellite?
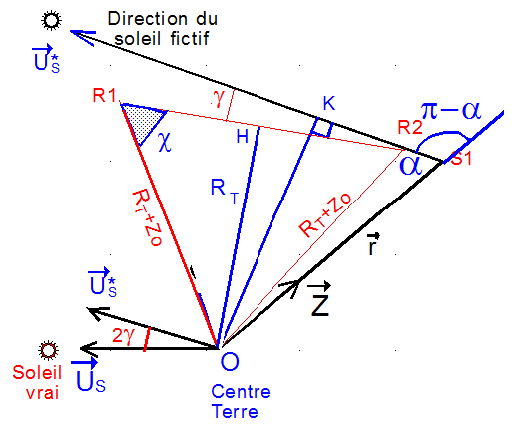
2°) Figures et notations :
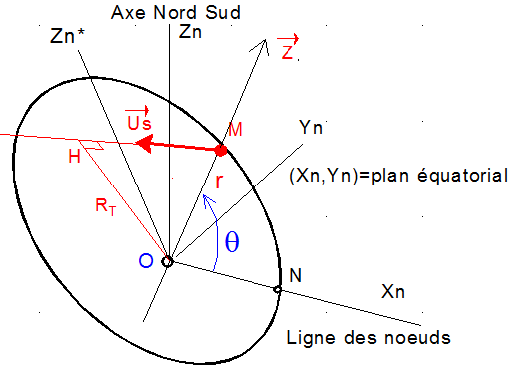
- Xn Yn Zn est le repère nodal associé à la ligne des nœuds
- (Xn Zn*) est le plan orbital et q l'angle polaire du point courant, mesuré sur la trajectoire circulaire à partir du nœud ascendant.
- M est une position d'entrée ou de sortie de l'éclipse, repérée par q, la figure montre MH la direction du soleil tangente à la surface terrestre.
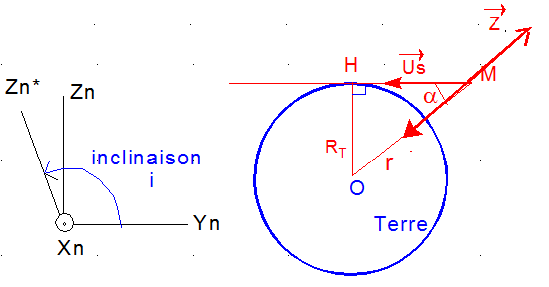
2°) Entrée ou sortie d'éclipse :
En bordure d'éclipse, la droite issue de la position satellite M et de direction Us est tangente à la surface terrestre, de plus le satellite doit être derrière la Terre. La situation d'éclipse limite est caractérisée par :
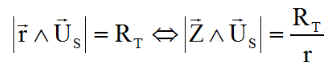
et
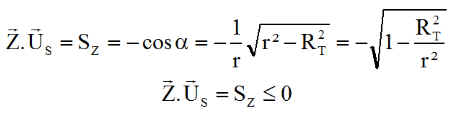
L'inégalité traduit la position de la terre entre le soleil et le satellite.
NB: La relation est la même pour l'entrée ou la sortie de l'éclipse, ce qui fera la différence c'est le saut de la puissance ( > 0 pour une sortie et < 0 pour une entrée )
Plus haut, nous avons déjà calculé le vecteur Us dans XYZ, ce qui rend aisée la traduction de la relation, grâce à la troisième composante de Us:
|
Équation en q des bords d'éclipse
Existence d'une éclipse, pour d fixé ou un jour fixé
|
On notera comme pour B et C, que la constante b = B/sin(ang) est toujours < 0 alors que c = C/sin(ang) peut changer de signe vers les jours 120,125 ou 275,280, suivant la valeur de H. La résolution est classique en posant :
![]()
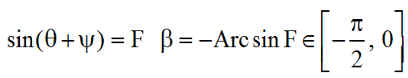
Dans ces conditions, une éclipse n'est possible que si |F| <= 1, ce qui donnera 2 solutions pour q notées q1 pour la plus petite valeur et q2 pour la plus grande.
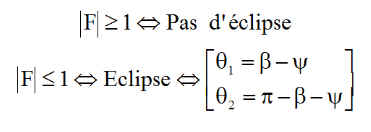
Géométrie de l'éclipse :
Pour le calcul de D = OH, le travail peut se faire dans Xn Yn Zn.
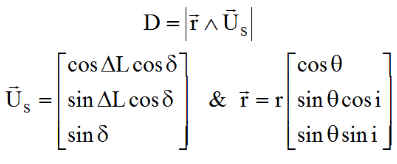
Regardons par exemple, si le nœud ascendant N est ou n'est pas en éclipse. Le calcul de D donne ainsi, pour q = 0
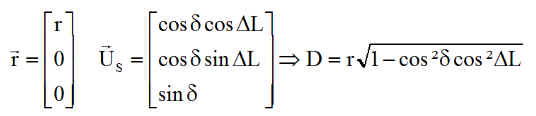
La traduction des 2 inégalités se résume simplement à une seule inégalité:
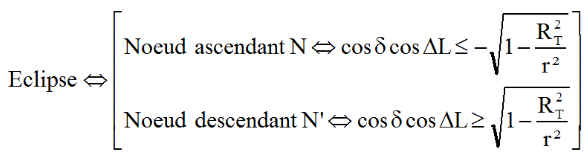
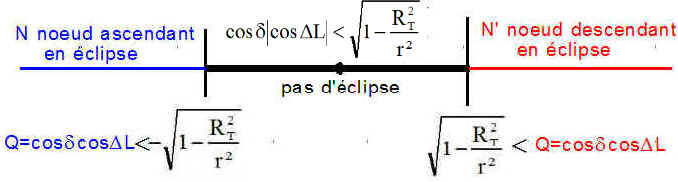
NB : Pour nos applications, avec r = 6993 km ( altitude 615 km ) et H = 20 h 30 ( DL = - 127°.5 ) ou 22 h 30 ( DL = - 157°.6 ), on peut vérifier que, quelle que soit la déclinaison, la relation est satisfaite au nœud ascendant, car par exemple pour H = 20 h 30
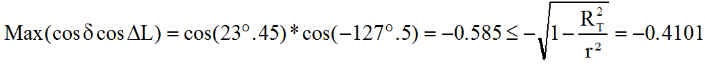
1 - Donc le nœud ascendant est pour nos satellites toujours en éclipse.
2 - Les valeurs calculées de q1 et q2 vérifient trois propriétés
a) que q2 > q1 car
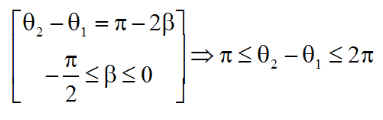
Remarque : ce résultat confirme de plus, qu'en éclipse la durée d'éclairement est supérieure à une demi période orbitale. On s'en doutait un peu !!!
b) que q2 est dans le troisième ou quatrième quatrième quadrant, et comme le nœud N ( q = 0 ) est en éclipse, obligatoirement la configuration ( pour notre satellite ) est la suivante, S1 et S2 sont de part et d'autre du nœud N , avec l'arc S2S1 d'éclipse inférieur à une demi orbite, ce qui va beaucoup nous simplifier les calculs.
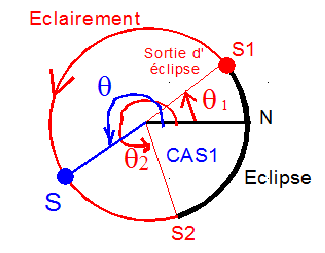
c) que q1 est toujours dans le premier quadrant. La connaissance de ce résultat n'est pas vraiment importante ni utile, mais elle aide à vérifier les calculs.
NB : Voir les calculs en annexe 1 et surtout l'étude géométrique qui confirme la configuration générale.
4°) Durée d'une éclipse : programme D:/tir_2019/laursurv/annexes.m
Conséquence : Comme S1 et S2 sont les "bords "de l'éclipse, avec un mouvement circulaire régulier, on a aisément la durée d'éclairement des panneaux. En la retranchant à la période, on trouve la durée de l'éclipse. On aura noté que b < 0 ce qui entraîne un éclairement plus grand que le temps d'éclipse.
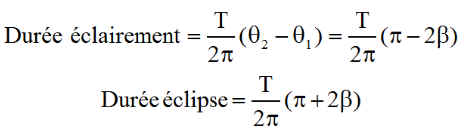
Exemple numérique : jour =175, c'est la formule du bas qui s'applique pour donner une durée d'éclipse de 1830 secondes
4°) Vérification numérique : programme D:/tir_2019/laursurv/annexes.m
Prenons des exemples, tous exécutés avec annexes.m permettant une vérification
a - Avec Z = 615 km, inclinaison i = 97°.85, H = 20 h 30, jour J = 175
On calcule la déclinaison solaire, d = 23.45*sin(2*pi/365*(284+jour)) = 23°.42 ( normal au voisinage du solstice d'été). DL = 15*(12-20.5) = -127°.5 q1 = 15°.174 est une sortie d'éclipse et q2 =261°94 une entrée-> résultat durée de 1830 s
b - Avec Z = 615 km, inclinaison i = 97°.85, H = 20 h 30, jour J = 270 ( sensiblement à l'équinoxe s'automne ) q1=41°.96 et q2=306°.21 ou -54°.79 ... on trouve une durée de 1548 s
c - Avec Z = 615 km, inclinaison i = 97°.85, H = 20 h 30, jour J = 100 ( sensiblement à l'équinoxe de printemps ) ... on trouve une durée de 1642 s
Dans notre simulation totale avec régulation, le satellite entre en éclipse 7562 s après survol du nœud ascendant et se termine 9204 s après. Dans tous les cas la confirmation est excellente.
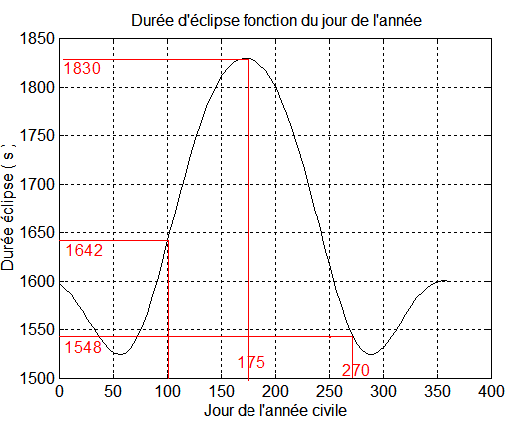
Cas H=20 h 30 Z=615 km i=97°.85
Conclusion : ces résultats valident nos calculs et la fonction qui calcule la durée des éclipses.
5°) Comment exploiter les transitions de puissance ?
Lors d'une transition de puissance, l'horloge du nanosatellite enregistre sa date actuelle T1 et à la suivante T2. Or le jour J, nous connaissons parfaitement les angles q1 et q2 qui nous permettent de remonter au temps écoulé depuis le passage au nœud ascendant, donc
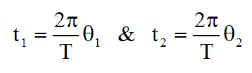
On eut donc en déduire 2 approximations de la date de passage au nœud ascendant, le satellite est maintenant localisé permettant d'estimer sa position à tout instant ultérieur, notamment au voisinage des pôles pour les prises de vue.
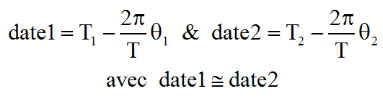
Une appréciation des erreurs est certainement nécessaire, nous en avons parlé plus haut, mais il se pourrait que la principale erreur provienne du retard à la détection de la transition d'entrée ou de sortie d'une éclipse.
III CALCUL DE L'ÉNERGIE REÇUE PAR ORBITE :
Bien évidemment les calculs ne concernent que les orbites héliosynchrones présentant une période d'éclipse, donc telles que
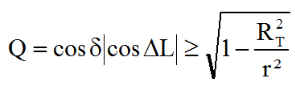

1°) Calculs pour nos satellites: Le nœud ascendant est toujours en éclipse.
Rappelons la relation de la puissance
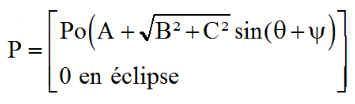
Le calcul de l'énergie doit simplement être effectué sur une orbite complète. Le changement de variable de t à q = w t = 2pt/T donne, pour le cas du nœud ascendant en orbite
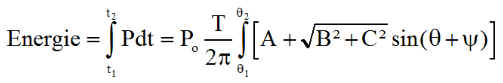
Les calculs détaillés de l'intégration, sont en annexe 3 et amènent ( compte tenu du temps d'éclipse ) à
|
Cas du nœud ascendant en éclipse
|
Rien ne laissait supposer qu'une expression littérale soit possible, en fonction des données de l'orbite. Étonnant!! Mais ceci ne vaut que pour les orbites héliosynchrones.
NB1 : Une fonction qui dérive de annexes est crée ( tir_2019/laursurv/PuissMNOP.m ) qui donne la durée de l'éclipse et la puissance moyenne du jour J de l'année.
PuissMNO(270)=[1548 7.01] Éclipse de 1548 s et puissance moyenne de 10.05 W.
La fonction qui calcule la puissance tout au long de l'année est tir_2019/laursurv/PmoyMNO.m
NB2 : Pour une orbite sans éclipse, la puissance vaudrait Pm = APo, puisque la partie sinusoïdale de la puissance a une intégrale nulle sur l'orbite entière, fermée.
2°) Résultats:
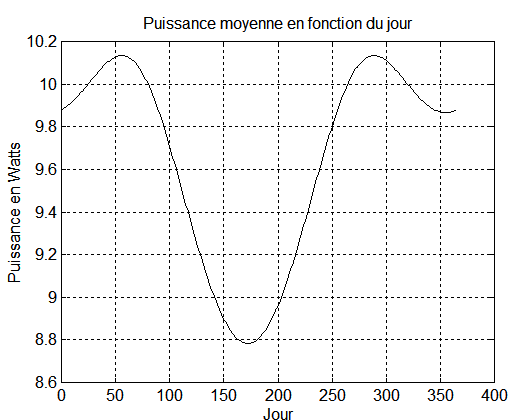
Conclusions:
1 - Ce graphe montre que pour H = 20 h 30 la puissance du pire cas ( vers jour 175 ) est de 8.8 Watts moyens par orbite et le meilleur cas de 10.125 W.
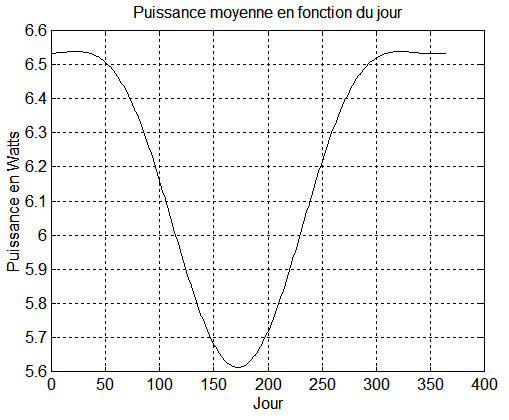
2 - Le graphe ci-dessous concerne l'heure H = 22 h 30, qui est nettement moins favorable, puisque le pire cas ne donne que 4.4 W de puissance pour 5.6 W dans la meilleure situation.
NB : Ces résultats sont confirmés excellemment par la simulation complète, sous régulation tir_2019/laursurv/new_sim1.m
| Jour | Cas | y | b | q1 | q2 | durée (s) | Pm (W ) | Énergie (W) |
| 1 | 1 | -117.16 | -40.63 | 9.88 | 337.8 | 1597 | 9.88 | 57514 |
| 65 | 1 | -90.23 | -42.69 | 41.55 | 312.89 | 1530 | 10.12 | 58868 |
| 80 | 1 | -80°.54 | -41.64 | 38°.9 | 302.19 | 1563 | 10.0 | 58202 |
| 175 | 1 | -48°.57 | -33.39 | 15°.17 | 261.94 | 1830 | 8.78 | 51126 |
| 270 | 1 | -84°09 | -42°.12 | 41°96 | 306.21 | 1548 | 10.05 | 58517 |
| 300 | 1 | -102.47 | -45°.63 | 59.845 | 325.1 | 1532 | 10.11 | 58839 |
NB : Toutes ces valeurs sont vérifiées par le programme tir_2019/lausurv/PuissMNO.m à initialisé par tir_2019/lausurv/new_dat.m ( Dans l'espace de travail donner courbe = 1 pour avoir le graphe de puissance, courbe = 3 pour vérifier les tests, courbe = 2 pour obtenir q1 et q2 en degrés)
3°) Compléments sur le cas du nœud descendant en éclipse:
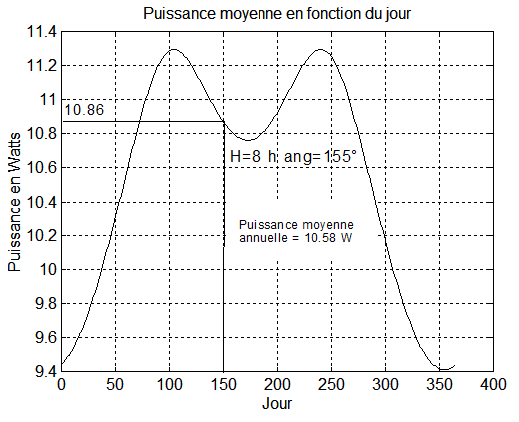
Exemple : H = 8 H --> DL = 60°, nous changeons simplement l'heure au nœud ascendant et bien évidemment, il faut retourner le satellite pour que les panneaux soient éclairés du bon côté, ce qui revient à changer ang en p - ang lors de l'initialisation. Pour le reste la formule reste la même. On pourra s'en convaincre enlisant l'annexe 2.
La relation ci-dessous
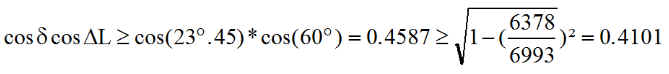
montre que le nœud descendant est en éclipse tout au long de l'année.
Le calcul de la puissance moyenne donne du jour 150 donne Pm = 10.87 Watts
IV OPTIMISATION DE L'INCLINAISON DES PANNEAUX
Rappelons l'expression de Pm pour un jour donné J de l'année ( J intervient dans la déclinaison d ), pour une orbite circulaire héliosynchrone où le nœud ascendant N est en éclipse
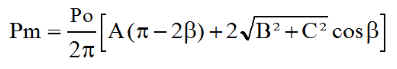
Commençons par simplifier l'expression, avec X = ang ( inclinaison des panneaux ):
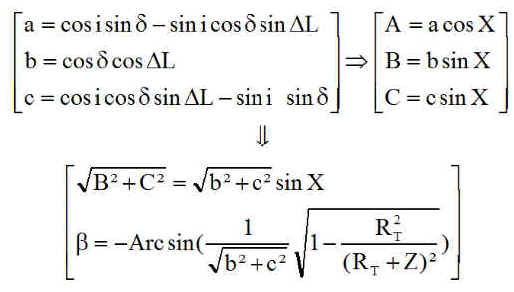
Rappelons que le satellite est sur une orbite à éclipse et donc satisfaisant avec les nouvelles notations à
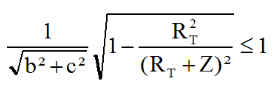
1°) Optimisation de l'inclinaison pour un jour J fixé :
Dans les calculs précédents, nous l'avons noté ang, et toutes les applications ont été faites avec X = ang = 35°. Posons nous la question de savoir si cet angle X=ang est optimum pour la mission. Écrivons autrement la puissance
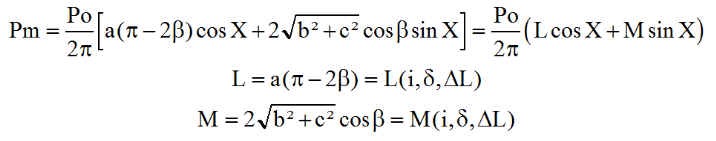
L'étude devient simple en remarquant que les coefficients L et M ne dépendent pas du tout de l'angle d'inclinaison X des panneaux. On peut donc écrire la loi de Pm:
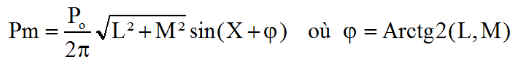
La puissance du jour J est donc optimale pour une inclinaison X donnant le sinus égal à 1:
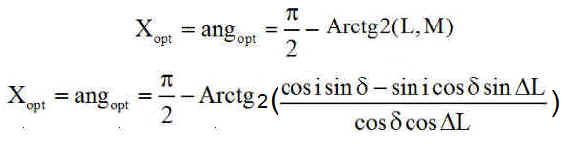
Remarques: il est étonnant de trouver une relation aussi simple pour un problème aussi complexe.
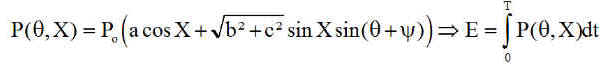
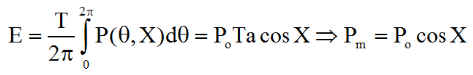
Cas particulier : On note que pour les orbites héliosynchrones sans éclipse H = 6 H ou H = 18 h, DL = 90° ou -90°. L'optimum est obtenu ( X = 0 ), donc pour une normale perpendiculaire au plan orbital, ce qui était prévisible.
1°) Optimisation de l'inclinaison sur l'année :
Pour moi, c'est la seule optimisation qui compte, puisque tous les jours, l'angle d'optimisation devrait être différent, ce qui n'est envisageable qu'avec une motorisation supplémentaire, mais pourquoi pas? Il s'agit donc de évaluer la moyenne des puissances sur l'année. Une expression intégrale doit être envisagée, avec comme variable d'intégration le jour J.
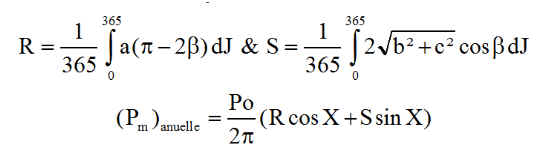
|
Puissance moyenne annuelle et inclinaison optimales
|
NB : bien évidemment, il faut recourir à l'informatique pour calculer les 2 intégrales R et S. Ce sera l'objet du programme TIR_2019/laursurv/Inc_Opti.m toujours initialisé par new_dat.m, il utilise les fonctions R_opti.m et S_opti.m pour le calcul des intégrales.
Quelques résultats pour illustrer :
a) H = 20 h 30 --> (Pm)annuelle = 10.17 W pour une inclinaison de 16°.64. Si on garde l'inclinaison de X=35° on obtient (Pm)annuelle = 9.78 W
b) H = 22 h 30 --> (Pm)annuelle = 6.38 W pour une inclinaison de 48°.58. Si on garde l'inclinaison de X=35° on obtient (Pm)annuelle= 6.2 W
En conclusion si les calculs sont corrects, l'heure locale est très pénalisante pour H=22 h 30 et mais une orientation des panneaux non optimale n'a pas de conséquences graves dans les 2 cas.
NB : pour essayer de valider les derniers calculs d'optimisation, je reprends celui de la puissance moyenne annuelle déjà calculée ailleurs. Ceci avec une formule approchée, genre somme de Riemann, de l'intégrale ( valable parce que la déclinaison varie peu d'un jour sur l'autre )
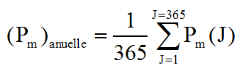
Pour H = 20 h 30 on trouve P = 9.68 W et 6.22 W pour H = 22 h 30
V TRAITEMENT PARTICULIER DE LA RÉFRACTION ATMOSPHERIQUE :
Il reste à étudier l'influence de la réfraction des rayons solaires par les couches atmosphériques. Physiquement la sortie S1 serait détectée un peu avant la sortie théorique et l'entrée serait retardée. Les éclipses sont moins longues.
1°) Géométrie de la réfraction :
Le plan de la figure contient le rayon vecteur OS1 et l'unitaire US du soleil à sa vraie position, à l'instant où le premier rayon issu du soleil frappe les panneaux solaires. Ce plan est différent en général du plan orbital. US* est l'unitaire du soleil fictif, vu par le satellite.
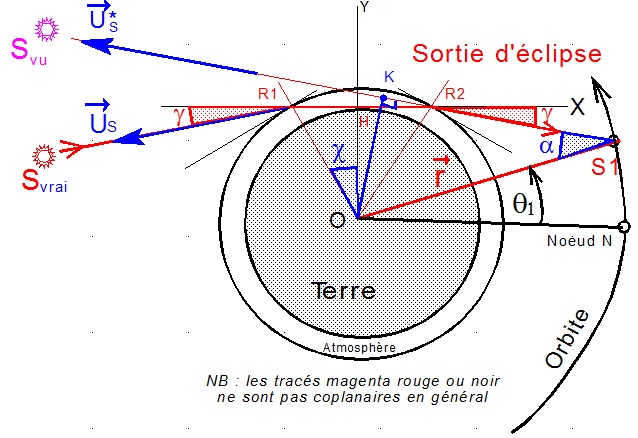
Le rayon limite issu du soleil vrai, subit 2 réfractions en R1 et R2 à l'entrée et à la sortie de l'atmosphère et il "tangente" la surface terrestre en H. Conséquence, le satellite "voit le soleil" non pas dans la direction US mais suivant l'unitaire U*S.
Données expérimentales: j'ai rencontré 2 articles concernant la réfraction atmosphérique et donnant un angle g = 36 ' d'arc ou un autre 0°.617. Dans les 2 cas c'est la même valeur. Les unitaires US et U*S font donc entre eux un ange de 2g . L'épaisseur de la couche atmosphérique utile est, dans ces articles, estimée à Z0 = 50 km
2°) Traduction de la condition de bord d'éclipse
Dans le plan de la figure, isolons les éléments importants. En pratique, tout se passe comme si la position limite du soleil est dans la direction Us* et donc que la distance minimum du centre de la terre à la ligne de visée est OK ( qui joue le rôle de RT dans le cas général sans réflexion )

Avec dans les triangles (O R1 H ) et ( O K R2 ) puis ( O K S1 ) on obtient
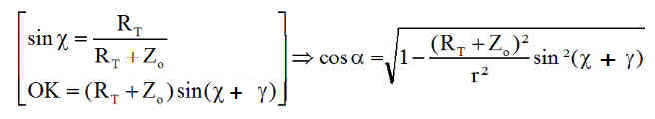
But à atteindre, trouver q tel que pour la position limite on ait.
|
|
NB : On constate qu'en l'absence d'atmosphère, on retrouve les calculs déjà réalisés plus haut, puisque g = 0 et c = p/2 redonnent
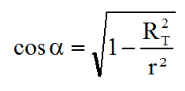
3°) Expression de U*S
Pour déterminer U*S, , dans le plan (Z, US ) nous posons 2 quantités à calculer l et m.
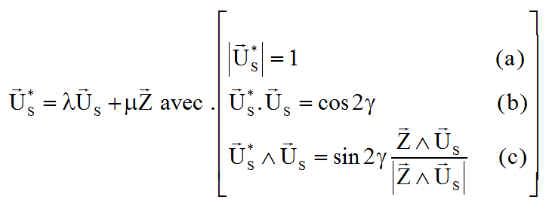
La condition (a) est évidente, (b) traduit l'angle entre les vecteurs, (c) traduit la position relative des 3 vecteurs dans le plan. Le système est redondant et permet une vérification notamment par (a) (vérification loin d'être explicite !!)
Reste à calculer les 2 quantités l et m.
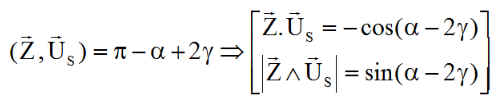
Le lecteur déduira aisément de ces relations
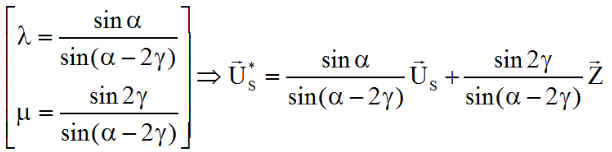
NB : on retrouve alors pour une terre dépourvue d'atmosphère ( g = 0 et c = p/2 ) que U*S = US rassurant!!
4°) Calcul de q1 et q2 :
a) Équation donnant l'angle q1 :
Nous traduisons l'équation (1) formulée plus haut, pour faire apparaître les vecteurs US et Z :
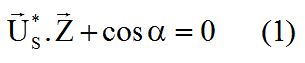

|
|
Remarque : il est réconfortant de retrouver que sans atmosphère, on a
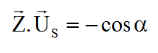
Ainsi, la nouvelle équation des angles polaires des bords d'éclipse est :
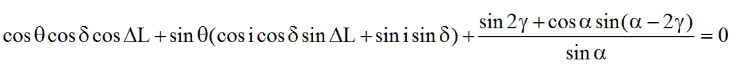
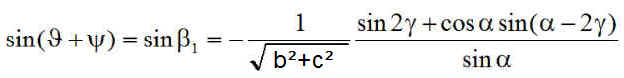
|
Résultats éclipses sur orbites héliosynchrones avec réfraction des rayons par l'atmosphère terrestre
|
Conclusions: ces calculs seront validés lorsque nous aurons comparé les durées d'éclipse avec ou sans réfraction. On devrait trouver des éclipses plus courtes en présence de la réfraction.
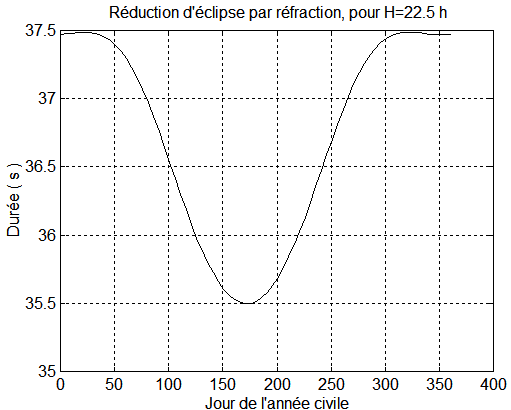
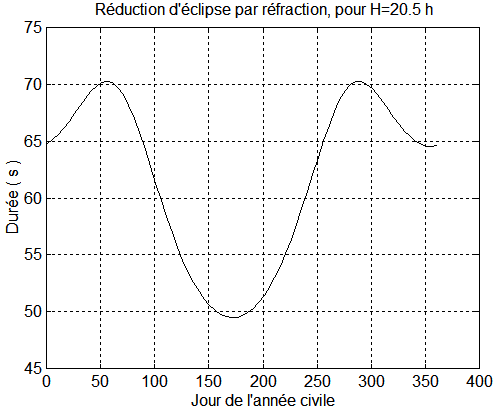
Une estimation très grossière ( car le plan orbital ne contient pas l'unitaire soleil ) pourrait consister à dire que le soleil est plus haut en déclinaison de 2g ( que sa déclinaison normale ) soit environ 1°.2, ce qui en cours d'année demande environ 1.2/23.5*91 = 4.65 jours ( 23°5 pour 3 mois environ ). Cet écart doit être multiplié par 2 ( entrée plus tôt et sortie plus tard), disons 9 à 10 jours. On regarde la variation de durée d'éclipse à 9 ou 10 jours d'intervalle. Par exemple 300 s en 75 jours, soit 4 secondes/jour. On devrait donc avoisiner l'ordre de grandeur de 40 secondes. Une vérification informatique du jour 175 donne 49 s, mais pour le jour 270 c'est 70 s. De plus le résultat dépend fortement de l'heure locale H comme le montrent les 2 graphes.
On constate donc, que si l'on utilise les éclipses pour une localisation, il faut absolument connaître cet "offset" d'avance. Quelques essais montrent que la valeur de Zo n'influe pas beaucoup sur l'écart, ce qui n'est pas le cas de l'angle g dont le pourcentage de variation se répercute à l'identique sur l'écart. Il faudrait pouvoir confirmer "une valeur sûre" de g .
Remarques : comme l'éclipse est plus courte de 1.25% environ, on peut en déduire un gain d'énergie du même ordre sur l'orbite.
Les résultats sont donnés par l'exécution ponctuelle de TIR_2019/laursurv/annexes.m ou ci-dessous plus générale par TIR_2019/laursurv/refract.m
VI MODE SURVIE QUASI INERTIELLE DU SATELLITE :
Le satellite, dans son mode nominal, est supposé stabilisé en pointage nadir où le repère satellite ( xyz ) est confondu avec le repère orbital (X,-Y,-Z ). Illustration par la position en "mgenta" sur la figure
Le mode survie doit permettre, avec une régulation à moindre coût, de produire un maximum d'énergie. Il faut donc rapprocher la normale aux panneaux de la direction du soleil. Po est la puissance optimale des panneaux.
![]()
Le mode survie adopté consiste à faire pivoter le satellite autour de l'axe y = -Y, d'un angle s, pour l'amener dans une position où l'angle entre l'unitaire US du soleil et celui N de la normale au panneaux solaires est minimal, ceci pour chaque jour J de la période de survie. Comme la déclinaison solaire varie très lentement dans le temps, le satellite garde une orientation quasi fixe dans l'espace absolu. D'où le nom de survie quasi inertielle.
A la limite si la survie est courte, on peut maintenir l'attitude fixe, l'esse.
Le repère de consigne pour la régulation de Laurens est donc le repère XC YC ZC qui gardera une orientation fixe tout le jour J ( si on veut être très précis on peut lui faire suivre une lente évolution suivant la déclinaison, donc J ). C'est pourquoi la survie est nommée "quasi inertielle".
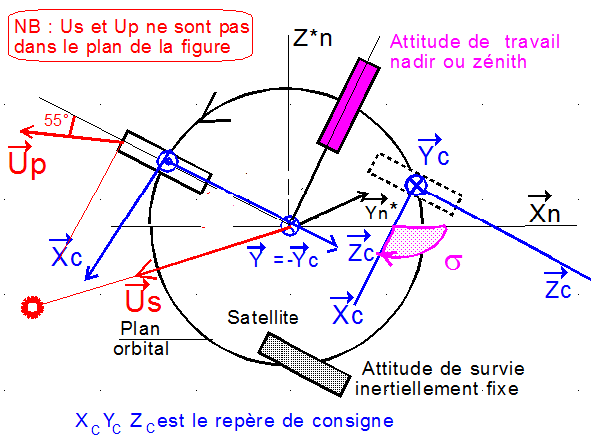
1°) Repères :
XN YN ZN est le repère nodal associé au nœud ascendant N, avec (XN,YN) comme plan équatorial.
XN Y*N Z*N est le repère qui se déduit du précédent^par une rotation d'angle i ( inclinaison orbitale ) autour de XN. Ainsi (X ,Z*N ) devient le plan orbital.
XC YC ZC est le repère de consigne pour la survie satellite. il se déduit du précédent, par une rotation d'angle s autour de Y*N. La figure montre ainsi un angle s > 0, cet angle ne dépend que du jour J de l'année.
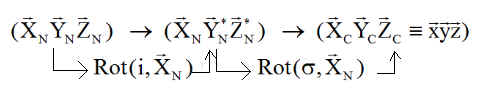
2°) Expression de la puissance P :
Le lecteur établira que la normale N aux panneaux a pour composantes en repère nodal :
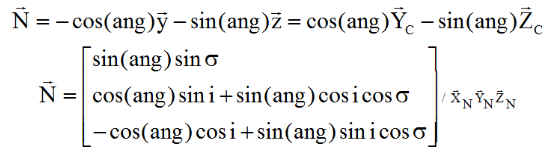
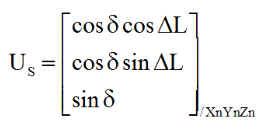
La puissance en découle par le produit scalaire, résumé en
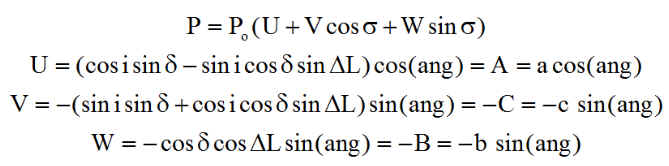
Il est rassurant de retrouver les mêmes quantités A, B, C a, b, c . Nous opérons la transformation classique:
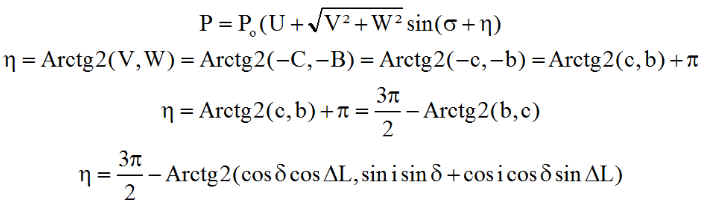
3°) Calcul de l'orientation optimale :
Avertissement important : une étude identique a déjà été réalisée, pour le satellite qui devait être lancé en 2017. Elle consistait à rechercher l'orientation inertielle du satellite, dans son plan orbital, autant dire l'axe y orienté suivant Y et les 2 autres restant fixe. La puissance qui avait été finement prise en compte, était la puissance réelle moyenne du jour J, compte tenu du temps d'éclipse. Il fallait donc optimiser Pm(J)
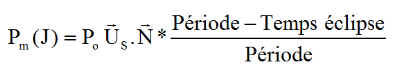
Ce qui ne change rien au calcul qui avait été réalisé par itérations. Les résultats sont strictement identiques à la nouvelle méthode littérale.
La survie adoptée doit donc conduire pour un jour J fixé, donc d fixé, à une puissance maximum. Ainsi le sinus de l'expression de P doit valoir 1, ce qui nous donne la valeur de s à choisir
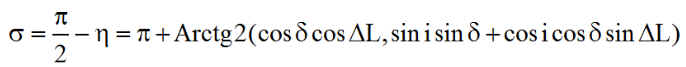
Remarque1 : Nous avons déjà trouvé plus haut, en mode nominal mais pas en mode survie
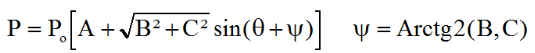
On retrouve pour s un lien étroit avec celle de y calculée plus haut.
Nous garderons comme conclusion, que l'orientation s en survie, est calculable, par une formule relativement simple.
|
|
Remarque2 : Il n'est pas étonnant que les relations donnant la puissance soient intimement liées, puisque dans le mouvement normal du satellite sur son orbite, il passe une fois par orbite et une seule dans la configuration où la puissance est maximale et de plus bien évidemment identique à celle de survie qui elle restera constante sur la journée. La figure ci-dessous montre la configuration. Le point délicat, c'est les angles et leur signe!!!
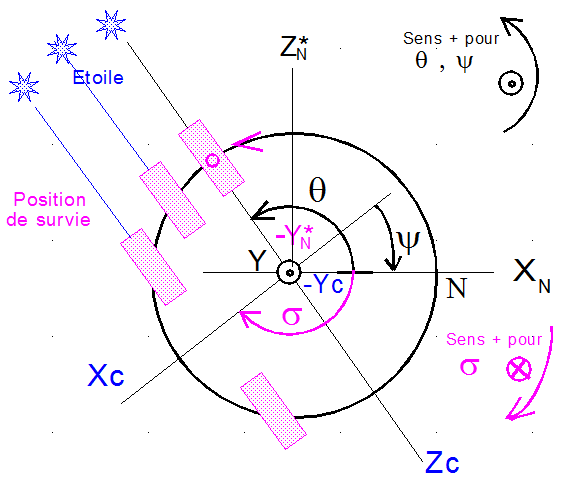
On a bien, compte tenu des signes
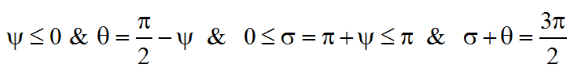
Remarque3 : Ce mode survie garantit donc une puissance constante sur toute une orbite, mais bien évidemment avec une lente variation en fonction du jour J de l'année. Les extrêmes sont bien sûr les mêmes que pour les puissances variables.
La puissance que nous considérons constante sur un jour vaut
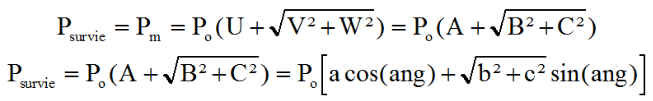
Fonction de vérification : TIR_2019/laursurv/survie.m initialisé par new_dat.m Écriture y=survie(u) avec u=[jour graphe] ( donner--> graphe=1, 2, 3, 4, 5, 6, 7, 8, 9 pour voir les courbes de --> s, durée éclipse, Pm, temps déclenchement après le nœud, la puissance optimisée en fonction de s , l'écart de puissance tout au long de l'année, la régulation simplifiée ), la régulation approchée à 2 orientations fixes, la régulation approchée à 3 orientations fixes. Donner aussi delta_sigma pour évaluer les erreurs et sigma_fixe pour un calcul particulier de puissance avec sigma non optimale.
AN : jour J = 150, un calcul précédent a donné y = - 50°.4, le programme survie donne s = 129°.6 on a bien s = p + y .
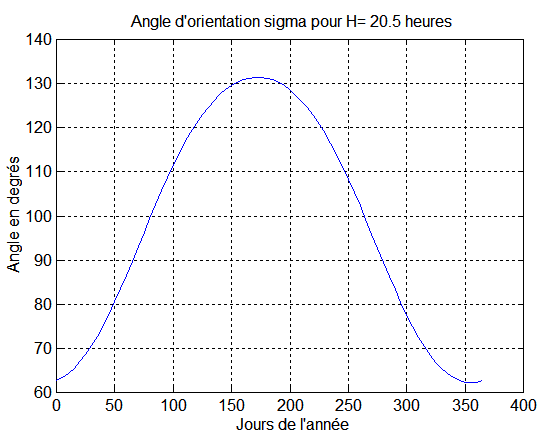
4°) Calcul du champ magnétique pour la consigne de survie :
On rappelle que :
- R0 = XYZ est le repère orbital
- le vecteur Bc de consigne a des composantes dans le repère satellite R que le vecteur champ magnétique réel B dans Rc.
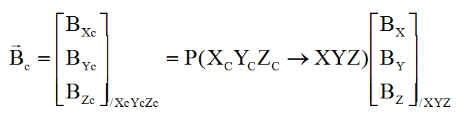
Prenant comme référence le repère nodal XNY*N Z*N , les 2 repères R0 =XYZ et Rc = XCYCZC y sont reliés simplement par ( le lecteur fera les calculs )
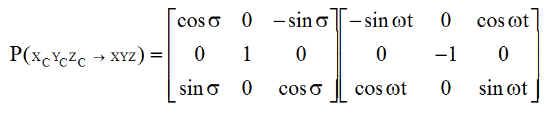
ou encore avec y
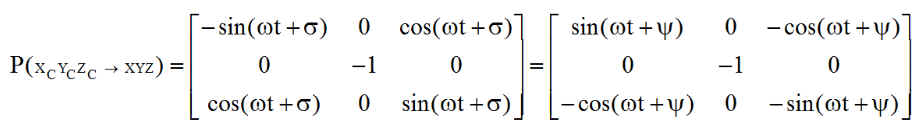
Remarque : pour nous rassurer, on constate que lorsque s+q=3p/2, on a confirmation de la position de survie par rapport au repère orbital de ce point particulier de l'orbite.
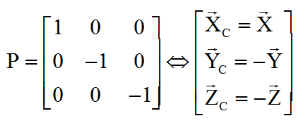
5°) Instant optimum pour déclencher la régulation de mise en consigne pour la survie :
Sans refaire une étude déjà réalisée pour le satellite précédent, il est apparu que le meilleur moment pour déclencher la mise en survie est lorsque le satellite passe par sa position inertielle future, souhaitée.
Donc, après le survol du nœud, au temps tN, on obtient
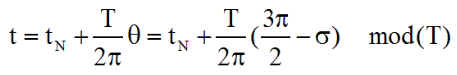
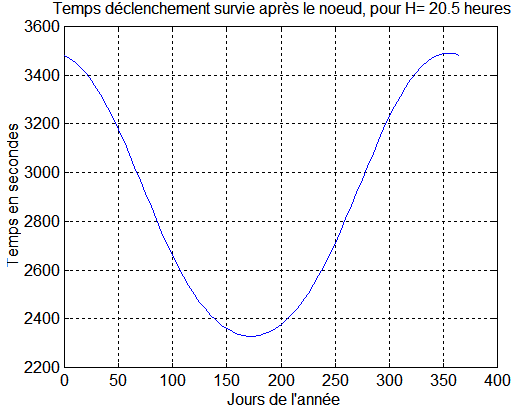
Remarque : Une étude analogue, plus complexe ( car la simplicité n'était pas apparue à l'époque), traitée avec les quaternions, avait conduit pour le jour 181, avec l'ancien satellite (H=21.5 et Z=817 km ) à un temps de déclenchement de 2804.5 secondes, que nous retrouvons très bien avec --> survie([181 1). Nous sommes ainsi rassurés sur l'ensemble des calculs, anciens et nouveau.
>>survie([181 0])
Vol: H= 21.5 heures Jour= 181 Inclinaison panneaux en degrés ang= 35
Puissance nominale des panneaux Po= 18 Watts
Orbite héliosynchrone d'altitude Z= 817 km, d'inclinaison i= 98.7 degrés
L'orientation du jour J= 181 est sigma= 123 degrés
Le temps de déclenchement survie du jour J= 181 est temps depuis nœud= 2480
secondes
Puissance moyenne optimisée du jour J= 181 est Pm= 11.03 Watts
6°) Influence d'une erreur de localisation sur la puissance en survie :
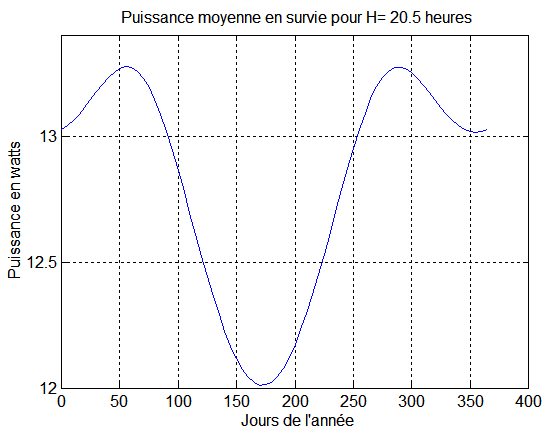
Nous supposons que la localisation résulte de la détection des transitions éclipse-éclairement des panneaux, et que l'accumulation des erreurs conduise à un écart DtN de 50, 100 ou 150 secondes, ce qui donne 3°, 6°, 9° d'écart en position orbitale et 300, 600, 900 km environ sur la trace sol. Quel est l'impact sur une survie qui devrait être programmée à ces moments là?
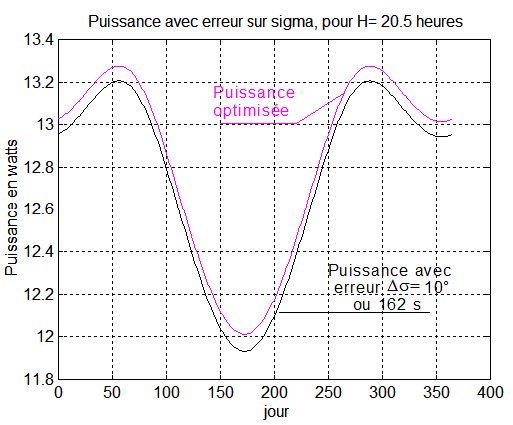
Puissance moyenne, compte tenu de l'éclipse
La courbe montre , dans le pire cas, qu'une erreur de 10° sur s ne produit au maximum qu'une perte de 0.07 Watts sur la puissance moyenne qui est de 12 Watts minimum. Il n'y a pas de quoi s'inquiéter!!
Une autre façon de retrouver ce résultat, consiste à reprendre l'expression de la puissance en fonction de l'orientation s, pas nécessairement optimale.
![]()
Considérons une erreur ne concernant que s autour du point où le sinus vaut 1 quand la puissance est maximum, ainsi si s0 est la valeur idéale telle que s0 +h = p/2 , nous aurons :
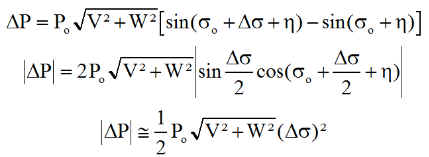
Pour conclure, il suffit de remplacer la racine et donc
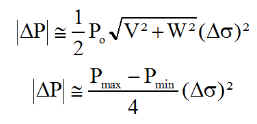
Dans le cas précédent, pour l'erreur maximum de 10° le maximum d'erreur de puissance est de 0.07 W. L'optimisation est donc très "robuste" et supportera une localisation approximative.
Remarque : il est logique de trouver, qu'autour de l'extremum de la puissance, la variation due à un écart angulaire soit du deuxième ordre par rapport à cet angle. Nous sommes en effet en un point de dérivée nulle , la "bosse" autour de laquelle les variations de la fonction sont très faibles. Même 30° d'écart ne donneraient que 0.7 W de perte moyenne.
CONCLUSIONS : Une orientation inertielle , la même pour toute survie, pourrait même être choisie sans trop de dommages, comme le prouve la courbe ci-dessous pour S = 90° quel que soit le jour de l'année. La puissance garantie reste quand même de 10.75 W minimum toute l'année.
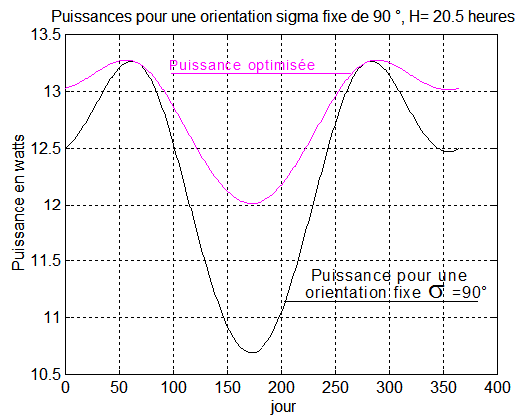
7°) Compromis pour une orientation inertielle par morceaux très proche de la solution optimale :
Pour rebondir sur cette remarque, peut être pourrait-on pour simplifier la programmation interne, et décider de 2 ou 3 survies simples, suivant l'époque de l'année. On y gagne en simplicité, peut-être en allégeant la programmation. La perte de puissance moyenne est très réduite, de l'ordre maximum de 0.5 Watts et pas sur toute l'année.
a) Cas de 2 plages et 2 orientations:
|
Compromis possible pour une régulation simplifiée [ 0 < jour < 100 et 265 < jour < 365 --> s = 90°] [100 < jour < 265 --> s = 130° ]
Le tracé bleu est sous optimal pour 0.41 W La courbe bleue ABCD, recoupement des 2 autres assure une puissance minimale inespérée, en toutes circonstances de 12 Watts avec une perte moyenne réduite à 0.5 W
|
Temps de déclenchement après survol du nœud : Évidemment ces temps doivent être appliqués respectivement dans les plages de jours ci-dessous. Le respect des temps est simplement une petite optimisation, sinon, toute heure est bonne.
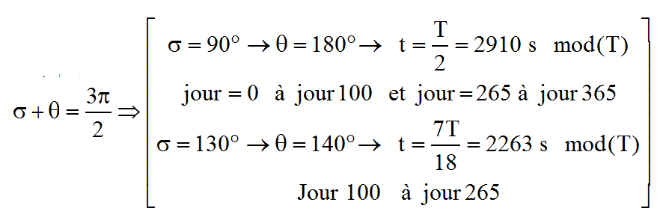
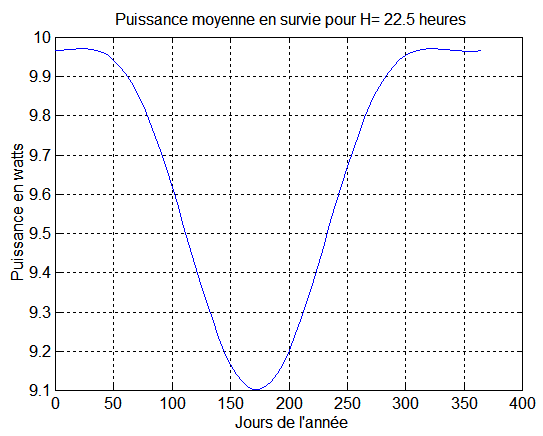
Une étude analogue pour H = 22.5 heures, donne une puissance assurée minimale de 9 Watts, en exploitant le graphe suivant:
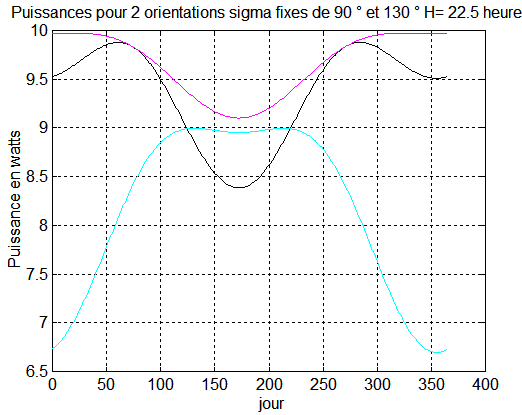
b) Cas de 3 plages et 3 orientations : ci dessous on utilise 3 orientations fixes en gros suivant les "saisons". Le lecteur pourra améliorer encore les choix des angles ou des jours, mais pour un gain de puissance très faible
| 0 < jour < 45 ou 300 < jour < 365 | s = 63° |
| 45 < jour < 95 ou 250 < jour < 300 | s = 90° |
| 95 < jour < 250 | s = 130 ° |
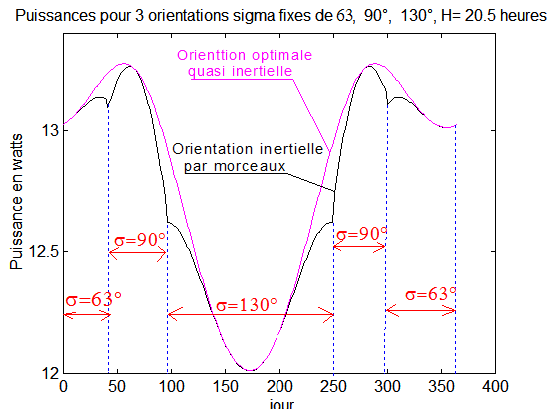
Le tracé noir est sous optimal pour 0.32 W
************** ANNEXES ****************
Annexe 0 -> Précaution de calcul
Précaution initiale qui fera gagner beaucoup de temps et évitera les erreurs d'angle.
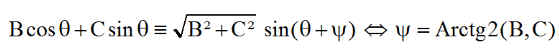
Si y est calculé avec Arctg(B/C) on arrive à une erreur lorsque B et C notamment ne sont pas positifs. Exemple convaincant:
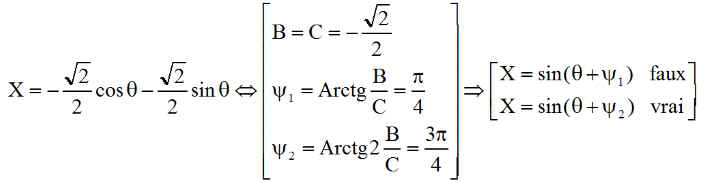
Annexe 1 -> cas où le nœud ascendant N est en éclipse
Il faut résoudre en q, une équation classique
![]()
![]()
qui peut se faire géométriquement en posant X = cosq et Y = sinq. Il faut alors trouver l'intersection du cercle unité et d'une droite d'équation DX+EY+cosa=0. La condition OH² = cos²a/ (D²+E²) <1 qui conduit à 2 solutions q1 et q2 avec comme convention q1 < q2.
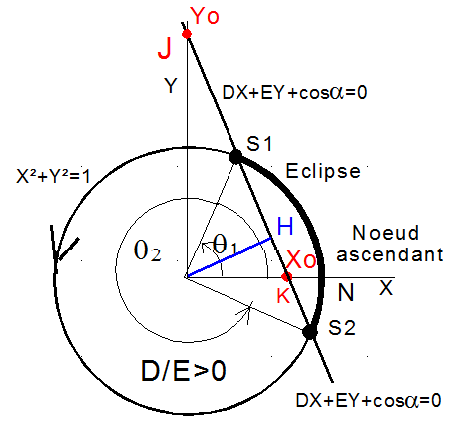
Cas héliosynchrone Z=615 km et H=20 h 30 avec D/E>0
Nous voulons montrer que S1 est dans le premier quadrant. Ce qui serait une certitude, si pour une pente - D/E < 0 de la droite J avait une ordonnée > 1. Quand la pente est > 0, l'ordonnée de J n'a plus aucune importance. Or D < 0, donc le cas à étudier est celui où E < 0
Démontrons les 2 affirmations suivantes ( pour H=20.5 ou 22.5 ):
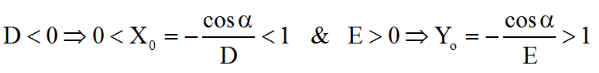
Nous connaissons les résultats ci-dessous
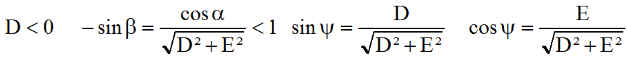
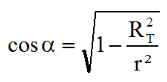
Donc
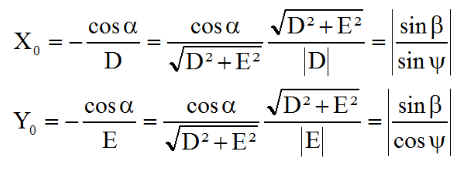
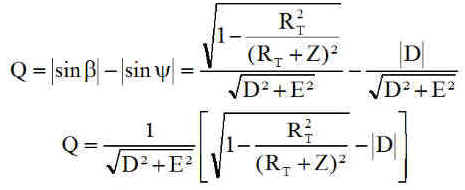
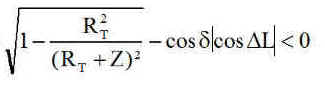
Donc Q < 0 et
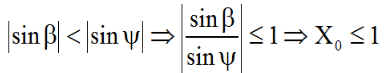
Un calcul informatique ( TIR_2019/laursurv/programme Absciss.m ) précise les coordonnées Xo et Yo, abscisse de K et ordonnée de L, pour les 2 heures locales qui nous intéressent. Le graphe ci-dessous montre que Xo reste toujours entre 0 et 1 pour les 2 cas qui nous intéressent, avec le nœud ascendant en éclipse.
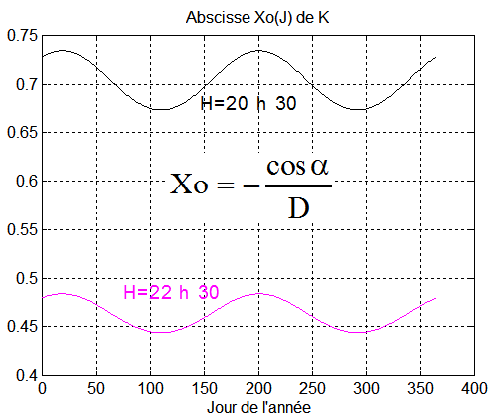
Vérification par programme (courbe=1;Absciss)
La démonstration que E < 0 entraîne |Yo| > 1 est laborieuse, en étudiant la fonction E de la variable d écrite sous forme sinusoïdale,( il n'est d'ailleurs pas sûr que des valeurs différentes de H ce soit valable ), on se contentera donc de la vérification pour H=20.5 et H=22.5 avec le tracé suivant:
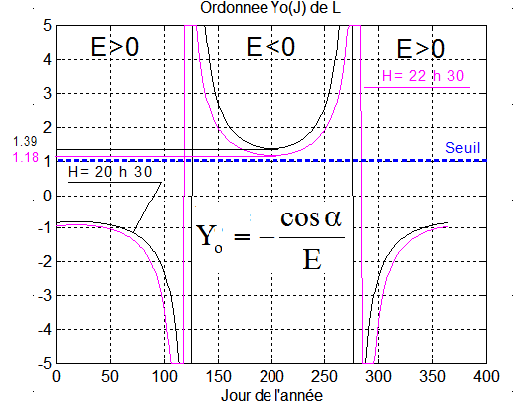
Vérification par programme (courbe=2;Absciss)
Conclusion: avec 0 < Xo < 1 et |Yo| > 1, la droite KL coupe nécessairement le cercle dans le premier quadrant, ce qui assure S1 dans le premier quadrant et 0 < q1 < 90°. Comme 0 < Xo < 1, la droite coupe toujours l'axe des X en K entre O et N, ce qui assure le nœud N est toujours entre les 2 points S1 et S2.
Ci dessous le second cas où D/E < 0 : S1 est le point de sortie d'éclipse et S2 celui d'entrée en éclipse.
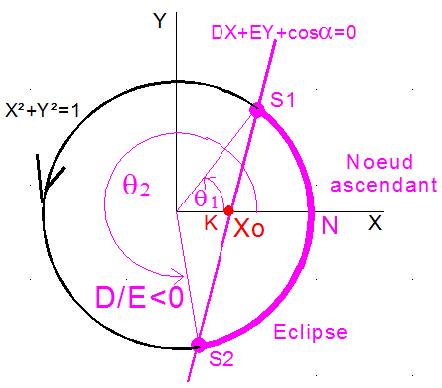
Cas héliosynchrone Z=615 km et H=22 h 30
Annexe 2 -> cas où le nœud descendant N' est en éclipse
La quantité Xo est alors comprise entre - 1 et 0, ce qui donne les configurations suivantes où S2 est le point d'entrée d'éclipse et S1 celui de la sortie de l'éclipse. Donnons, pour la figure, le cas D/E < 0
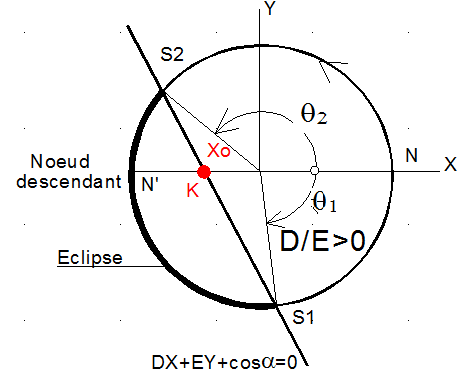
Annexe 3 ->
Énergie et puissance moyenne sur une orbite du jour J :
Dans tous les cas elles se calculent de la même
façon par une intégrale sur la partie éclairée de l'orbite:
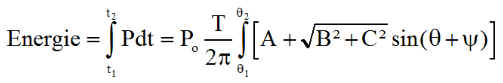
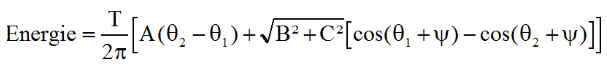
Compte tenu des valeurs de q1 et q2 calculées plus haut
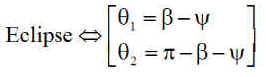
il vient une relation remarquablement simple:
|
Cas du nœud ascendant en éclipse
|
Pour mémoire : les programmes utilisés
1 - annexes.m --> programme avec sorties commentées, pour de multiples contrôles ponctuels, au départ de l'étude
2 - PuissMNO.m --> fonction pour calculer la puissance réelle du jour J comme entrée et 1 pour les commentaires et 0 sans commentaires. Syntaxe >>PuissMNO([J 1]) en sorties y=[temps_eclipse Pm cas test energie teta1 teta2];
3 - PmoyMNO.m --> donne la puissance moyenne annuelle et présente pour courbe=1, la courbe de puissance, courbe=2 les angles q1 et q2 . Syntaxe >> PmoyMNO
4 - Absciss.m --> routine de calcul de l'abscisse Xo et de l'ordonnée Yo pour la géométrie de recherche des racines. Obtention des courbes en donnant avant courbe= 1 ou 2
5- a) fonctions R_Opti.m et S_Opti.m utiles pour l'optimisation de l'inclinaison des panneaux.
b) programme Inc_Opti.m appelle les 2 fonctions précédentes et donne dans l'espace de travail
Inclinaison optimale sur
l'année
Puissance moyenne optimale sur l'année en W
Puissance moyenne annuelle avec l'angle imposé non optimal de 35°, en W
6- survie.m pour l'optimisation de la survie quasi inertielle. Donner
- graphe=1 pour l'angle d'orientation s
- graphe=2 pour la durée des éclipses
- graphe=3 pour la puissance moyenne
- graphe=4 pour le temps de déclenchement de la survie, après passage du nœud.
- graphe=5 --> Puissance fonction de sigma
- graphe=6 --> Courbe de perte de puissance pour un écart par rapport à sigma optimal
- graphe=7 --> Courbes de puissance pour l'orientation sigma fixée à 90° ou 130° ou sigma optimisée
- graphe=8 --> Courbe simplifiée de puissance pour l'orientation sigma à 90° ou 130° et sigma optimisée
- graphe=9 --> Courbes simplifiée de puissance pour l'orientation sigma fixée à 63°, 90° ou 130° et sigma optimisée
NB : tous dans TIR_2019/laursurv et initialisation par new_dat.m on peut aussi les retrouver tous dans TIR_2019/routines
*************************************
Exemple de résultats de annexes.m
***********************************
Vol: H= 20.5 heures Jour= 361 Inclinaison panneaux en degrés ang= 35
Puissance nominale des panneaux Po= 18 Watts
Orbite héliosynchrone d'altitude Z= 615 km, d'inclinaison i= 97.85 degrés
Orbite à éclipse, durée d'éclipse de 1599 s pour une période de 5820 s
Déclinaison solaire du jour 361, delta= -23.31 degrés Longitude nodale du
soleil DL= -127.5 degrés
Constantes : A= 11.44 B= -5.772 C= -3.02
Angles en degrés: teta1= 77.09 teta2= 338.2 Beta= -40.53 psi= -117.6
Puissances moyennes journalières calculées du jour 361 de l'année
Avec teta1 et teta2 ---> Pm= 9.871 W
Avec beta ---> Pm= 9.871 W
Avec L et M ---> Pm= 9.871 W
L'énergie du jour 361 est de 5.745e+004 Joules
Puissance minimale du jour Pmin=4.925 W et maximale Pmax=17.95 W
******************************************** Cas avec réfraction
***********************************
Angle de réfraction gamma= 0.6 degré, épaisseur atmosphère Zo= 50 km
Durée d'éclipse avec réfraction des rayons solaires D= 1544 secondes
Eclipse : Entrée retardée ou sortie avancée de 27.66 secondes
Angles en degrés: teta1= 75.38 teta2= 339.9 Beta1= -42.24 psi= -117.6
******************************************** Fin du cas avec réfraction
***********************************
Tous les tests sont vérifiés, les formules de calcul sont donc validées
Constantes pour la moyenne annuelle de puissance L= 3.535 M= 0.9591 psi= -117.6
degrés
********************************** FIN DES RESULTATS DE annexes.m
*********************************
survie([130 9])
**************************** RESULTATS ***********************
Vol: H= 20.5 heures Jour= 130 Inclinaison panneaux en degrés ang= 35
Puissance nominale des panneaux Po= 18 Watts
Orbite héliosynchrone d'altitude Z= 615 km, d'inclinaison i= 97.85 degrés
ATTENTION, les puissances moyennes tiennent compte des durées d'éclipses
L'orientation du jour J= 130 est sigma= 124.7 degrés
Le temps de déclenchement survie du jour J= 130 depuis le noeud est de 2349
secondes
Puissance moyenne optimisée ( Eclipses prises en compte ) du jour J= 130 est
Pm= 12.37 Watts
Puissance minimum non optimisée des panneaux du jour J= 130 est Pmin= 4.529
Watts
Puissance maximum non optimisée des panneaux du jour J= 130 est Pmax= 17.92
Watts
Pour un écart d'orientation optimale de 30°, la perte maximum de puissance
moyenne est de 0.644 Watts
PUISSANCE MOYENNE ANNUELLE OPTIMISEE ( compte tenu des éclipses ) = 12.82 Watts
------------------------ Approche simplifiée sous optimale
---------------------
Pour l'approche à 2 orientations constantes, 90 , 130° la perte maximum de
puissance moyenne est de 0.4091 Watt
Pour l'approche à 3 orientations constantes, 63, 90, 130° la perte maximum de
puissance moyenne est de 0.3186 Watt
---------------------------------------------------------------------
NB :Avec au départ graphe=1 à 6, il vient les courbes:
graphe=1 --> Angle optimal d'orientation sigma fonction du jour de l'année
graphe=2 --> Durée d'éclipse
graphe=3 --> Puissance optimale fonction du jour de l'année
graphe=4 --> Temps de déclenchement de la mise en survie
graphe=5 --> Puissance fonction de sigma
graphe=6 --> Courbe de perte de puissance pour un écart par rapport à sigma
optimal
graphe=7 --> Courbes de puissance pour l'orientation sigma fixée à 90° ou
130° ou sigma optimisée
graphe=8 --> Courbe simplifiée de puissance pour l'orientation sigma à 90°
ou 130° et sigma optimisée
graphe=9 --> Courbes simplifiée de puissance pour l'orientation sigma fixée
à 63°, 90° ou 130° et sigma optimisée
---------------------------------------------------------------------
***************************************************************************
PuissMNO([270 1])
************************************* RESULTATS DE PuissMNO.m
***********************************
Vol: H= 20.5 heures Jour= 270 Inclinaison panneaux en degrés ang= 35
Puissance nominale des panneaux Po= 18 Watts
Orbite héliosynchrone d'altitude Z= 615 km, d'inclinaison i= 97.85 degrés
Durée d'éclipse du jour 270 de l'année: 1548 secondes
Puissance moyenne du jour 270 de l'année: 10.05 Watts
Angle teta1 du jour 270 de l'année: 41.96 degrés
Angle teta2 du jour 270 de l'année: 306.2 degrés
************************************* FIN DES RESULTATS DE PuissMNO.m
***********************************
PmoyMNO;
*************************************
RESULTATS DE PmoyMNO.m ***********************************
Vol: H= 20.5 heures, inclinaison panneaux en degrés ang= 35
Puissance nominale des panneaux Po= 18 Watts
Orbite héliosynchrone d'altitude Z= 615 km, d'inclinaison i= 97.85 degrés
*******************************************************
Puissance moyenne annuelle Pm_annuelle= 9.679 Watts
*******************************************************
************************************* FIN DES RESULTATS DE PmoyMNO.m
***********************************
******************** FIN 07/02/2017 **********************