TENTATIVE DE MISE EN SPIN AUTOUR

 DE LA 

DIRECTION NORMALE AUX PANNEAUX

Par avance, c'est un échec !!! dont je ne connais pas vraiment les raisons

******************************

Je donne ma conclusion avant l'étude : la mise en spin autour de y1 me paraît impossible, probablement par la conjonction de 3 raisons :

- La direction y1 de la normale panneau donne une inertie moyenne, pas de quoi "raidir" une rotation

- La direction y1 de la normale panneau donne un produit d'inertie très grand a qui a un effet déstabilisant, par vibrations importantes.

- Le gradient de gravité est peut-être déstabilisant.

Peut-être faudrait-il penser pour CASAA-SAT à l'équilibrer pour aboutir à une matrice diagonale. Est-ce faisable?

I AUTRE MODE DE SURVIE  PRIVILEGIANT L'ENERGIE?

Pour notre nanosatellite, les panneaux solaires, contrairement au microsatellite SumbandilaSAT, ne sont pas sur la face y+ mais orientés de biais avec une normale dans le plan ( y z ) du satellite.

Il me semble qu'une solution efficace de mode survie pourrait consister :

-  à "spinner" , dans un premier temps le satellite autour de la normale aux panneaux, avec un spin négatif

-  dans un deuxième temps opérer la régulation alternée précession vers le soleil hors éclipse et contrôle du spin en éclipse.

1°) PRELIMINAIRES :

a) Nouveau repère : R1 : x1 y1 z1 est un repère lié au satellite avec x1 = x , y1 = - N, z1 qui complète

On passe de xyz à x1 y1 z1 par une rotation autour de x ou x1 d'angle +35°

GROS PROBLEME ?

Pour moi la matrice de passage de xyz à x1 y1 z1 est

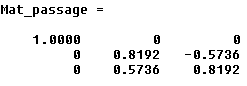
Et la nouvelle matrice Asat1 est 

Asat est la matrice d'inertie du satellite dans x y z, V donne les axes principaux dans x y z et D donne la matrice diagonale diagonale  et donc les moments principaux.

Asat1 est la matrice d'inertie du satellite dans x y1 z1, V donne les axes principaux dans x1 y1 z1 et D donne la matrice diagonale diagonale  et donc les moments principaux.

REMARQUE  : Les résultats sont cohérents. Ce qui me laisse à penser que ma nouvelle matrice d'inertie est correcte !! Au passage on observe 2 choses :

- Que pour Asat, les axes principaux sont quasiment x y et z et donc des produits d'inertie faibles. De plus l'axe y est l'axe d'inertie maximale.

- Que pour Ast1, les axes principaux sont très distincts des axes X1 Y1 Z1 et donc un produit d'inertie  I_TL=0.0074 est important. Ceci pourrait entraîner une instabilité de la rotation axiale autour de y1 ( L'équivalent des vibrations dune roue de voiture mal équilibrée ). Maintent on constate aussi que l'axe y1 est l'axe d'inertie moyenne .Quand une matrice est diagonale la rotation autour de l'axe d'inertie moyenne est instable, en l'absence de tout couple ; Mais je ne peux pas conclure car la matrice Asat1 n'est pas diagonale et de plus on exerce des couples.

Pourquoi ai-je un problème? 

Je me suis dit qu'avant de reprogrammer une régulation qui "spinnerai" le satellite autour de y1 en éclipse et précessionnerait vers le soleil hors éclipse, je pourrais simuler la situation de la manière suivante ( c'est peut-être là que je me trompe, mais pourquoi ):

- Je simule d'abord la régulation alternée comme si CASAA-SAT avait ses panneaux solaires sur la face y-. Les résultats sont ceux que je te donne plus haut. La matrice d'inertie est Asat dans xyz

- Je remplace Asat par Asat1 qui est la matrice d'inertie du satellite dans x1 y1 z1 et je refais la même simulation, Pour moi, ce que j'ai fait équivaut à mettre les panneaux sur la face y1-. Donc, au détail près final qu'il faudra remettre les moments magnétiques sur les axes xyz ( en transformant M1 en M par la matrice P ), pour moi je pensais que c'était pareil. 

Mais alors pas du tout, toutes les vitesses sont déstabilisées, l'énergie produite chute de plus de 50 % ainsi que la puissance, la précession n'a plus d'effet évident. Le mouvement est chaotique, il doit y avoir des retournements complets car la puissance s'annule.

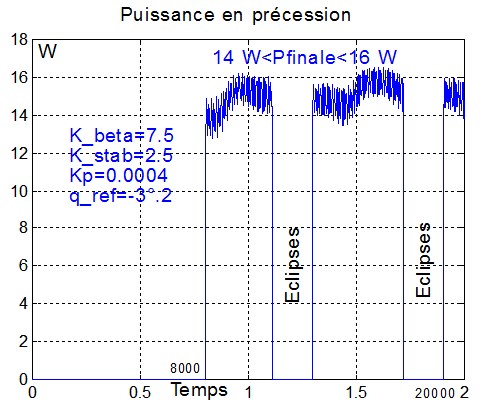
Voilà ce que devient la précession, chaotique convergence inexistante!!

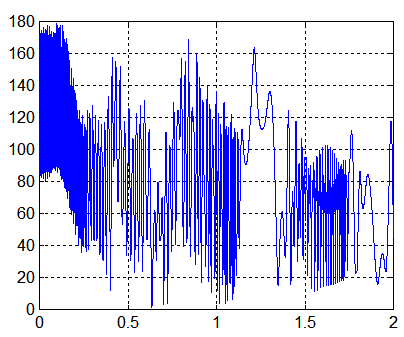
et la courbe de puissance qui laisse deviner  (puisqu'elle s'annule souvent) que le satellite passe tête-bêche. Est-ce le signe d'une instabilité ?

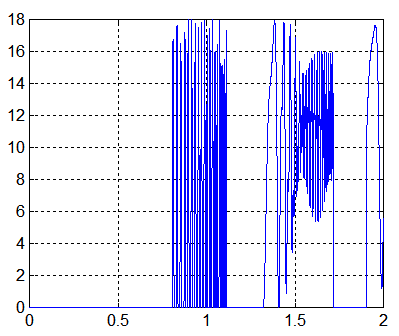
TTENTION : Si tel était le cas, ceci enlèverait tout espoir d'utiliser la mise en spin autour de la normale panneaux?

AUTRES INFOS :

Si, au lieu de supposer que l'inclinaison de l'axe antenne sur y est 35°, je prends 90°, ce qui veut dire que les panneaux seraient sur la face z-, la simulation marche très bien, certes un peu plus lente, mais le niveau de puissance  maximale est presque atteint, la régulation paisible et les moments magnétiques très réduits.

Je suis de plus en plus perplexe!!! Car l'axe z est celui d'inertie minimale pour Asat

Un essai sans gradient de gravité donne des résultats nettement meilleurs, mais non satisfaisant. Il est vrai que les inerties jouent sur le gradient.

SUITE ET FIN ( peut-être !!):

J'ai tout d'un coup pensé que si c'est un problème de classement des moments d'inertie, je pourrais changer cet ordre, juste ce qu'il faut sans alourdir trop le satellite. J'ai donc ajouté 2 masses symétriques sur les faces x+ et x-, ce qui ne change pas x mais modifie I₂₂ et I₃₃ . 

Adjonction de 2 masses : J'ai donc ajouté 2 masses symétriques sur les faces x+ et x-, ce qui ne change pas x mais modifie I₂₂ et I₃₃ . 

Sauf erreur de calcul de ma part, une augmentation de 0.004 m²-kg avec 2 masses symétriques sur l'axe x, à 5 cm de l'axe, coûterait plus 1.2 kg, ce qui prohibitif.

La simulation fonctionne correctement ( spin -2°/s et Kp=0.0028 ), avec une puissance moyenne de 9 w, mais la précession est lente seulement vers 30 à 35° du soleil!! L'augmentation du spin est catastrophique et la puissance baisse.

**********************  SUITE SANS INTERÊT **********************

3 - Calcul du moment d'inertie autour de la direction normale aux panneaux

=

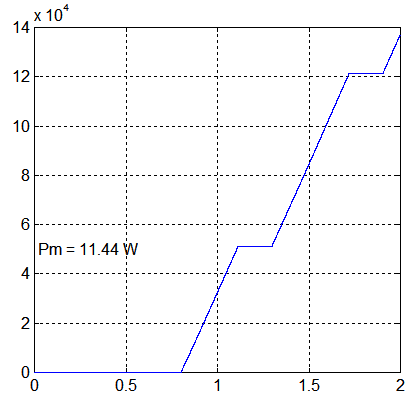
Nouvelle simulation ang=0 Kp=0.0004 K_beta=7.5  Kstab = 2.5 q_ref=-6°.4

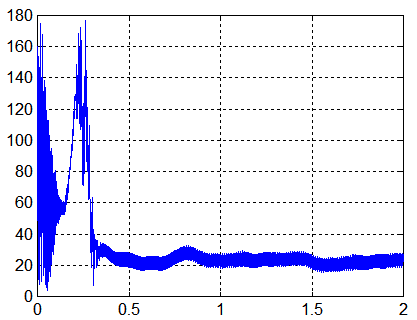
Angle de  rattrapage y et -Us

***************************

b) Matrice P changement de base : 

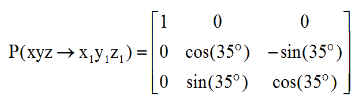
d) Calculs des données nécessaires : On rappelle t=0 au dessus de l'équateur

* L'unitaire pointant le soleil est calculable par les relations ci-dessous. Ceci à condition que l'orbite soit assez bien connue, au moment du calcul. En ce qui concerne l'héliosynchronisme, les paramètres orbitaux seront déterminés par un propagateur d'orbite embarqué et mis à jour régulièrement par une remontée des TLE.

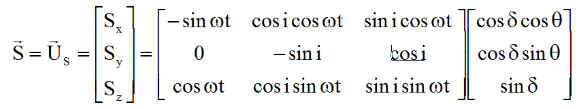
Sinon, un capteur de position du soleil comme pour le microsatellite SumbandilaSAT, donnerait directement à bord les composantes Sx Sy et Sz.

* Les composantes du champ magnétique terrestre  B sont elles évaluées par un magnétomètre 3 axes correctement filtré.

* Hy₁ = I(satellite/y1 )* q_ref. le moment d'inertie s'évalue avec la donnée initiale de la matrice d'inertie Asat du satellite.

On trouve  I_t = 0.0191 m²-kg

Remarque : la matrice d'inertie, dans les nouveaux axes devient Asat1, avec y1 est l'axe de petite inertie . L'axe y1 est celui de moyenne inertie, qui pourrait porter une rotation instable ( ce qui serait certain si la matrice d'inertie était diagonale )

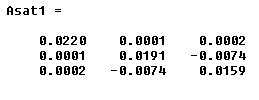
NB : Les moments d'inertie ( kg.m2) doivent respecter les conditions suivantes :- Tangage (I yy) > Roulis (I xx) > Lacet (Izz) - Les autres termes doivent être négligeables devant les termes diagonaux Or ici 0,025 > 0,022 > 0,01 et les les autres termes sont négligeables devant les termes diagonaux. 

? Ce n'est pas le cas ici!!

c) Passage dans le repère R1 :

Le changement de base donne  

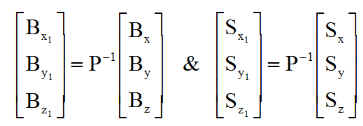
d) Régulation de précession :

Elle se déduit du cas d'alignement de y sur Us, en l'adaptant en y₁ vers Us₁.

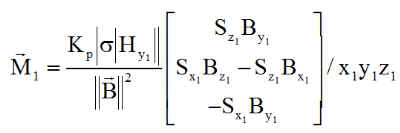
e) Calculs des moments magnétiques de commande :

Comme les actuateurs sont disposés sur les axes initiaux xyz du satellite, il faut revenir aux valeurs dans ces axes, donc

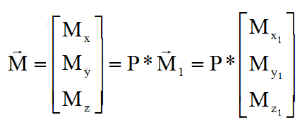
2°) ESSAI EN SUPPOSANT LA FACE y- COUVERTE DE PANNEAUX :

Simulation c:/casasurv/surv_sim.m initialisée par surv_dat.m

Matrice d'inertie normale et commande alternée de mise en spin en éclipse et de précession vers le soleil hors éclipse. jour=81 soit équinoxe de printemps

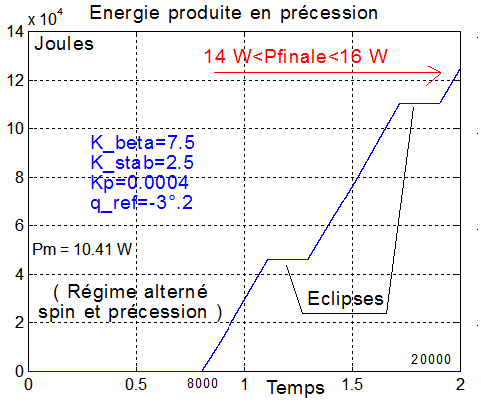
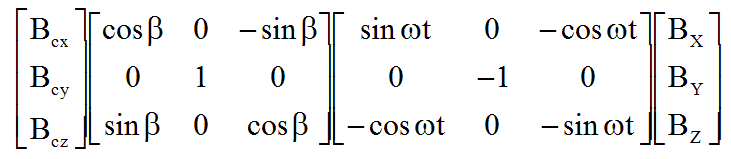
Angle entre -y et Us ( direction soleil )

Exemple de mise en spin ( méthode de Laurens )

autour d'un axe fixe par rapport au satellite ou encore xyz

Ci-dessous le lacet, apparemment très stable ( axe_spin=[0 0 1] )

de même que le spin autour du tangage ( axe_spin=[0 1 0] )

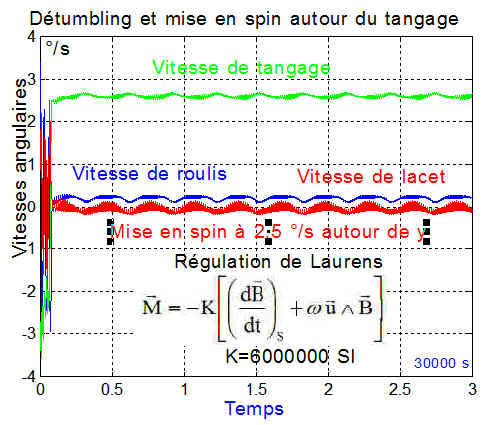
Le spin en roulis tente de s'établir mais est visiblement périodiquement instable ( axe_spin=[1 0 0] ), entraînant par couplage une instabilité sur tous les axes

Pour finir, voici la mise en spin autour d'une direction parallèle à l'axe des panneaux  ==> axe_spin=[0 -cos(35*pi/180) -sin(35*pi/180)];

Les vitesses angulaires sont chaotiques

Le tracé de la vitesse angulaire de spin autour de la normale, donne avec la projection adéquate sur l'axe de spin choisi  ==> plot(temps,(p*axe_spin(1)+q*axe_spin(2)+r*axe_spin(3))*180/pi)

Nous sommes loin d'un état stable!!!

Conclusion : en cause probablement la position moyenne des inerties autour de x et de la parallèle à la normale. Affaire à confirmer!!!

Cette nouvelle simulation totalement indépendante de celle de Steyn, semble confirmer l'impossibilité de "spinner" le satellite autour d'un axe parallèle à la normale aux panneaux. Sauf, bien sûr à revoir la géométrie du satellite!!!