![]()
DETUMBLING PAR " EFFET BOUSSOLE "
&
CONTRÔLE DE L'ANGLE DE ROTATION
AUTOUR DE B
![]()
La simulation REGBOUS3/REGBOUX2.M & LAURDAT1.M ( conservées telles qu'elles existent au moment de la rédaction ) montrent que rapidement les unitaires de B et Q ne diffèrent que de 2°
1 - Que Bc tend vers B
2 - Que PB-B tend vers le vecteur nul, confirmant 1
3 - Que les vecteurs unitaires de la rotation Q et du vecteur champ magnétique convergent l'un vers l'autre. Ce qui montre que les repères R et R0 se correspondent par une rotation autour de la direction du champ B.
4 - Dans le cas présent, la rotation à effectuer est de l'ordre de 138°. D'ailleurs, la première composante du quaternion vaut environ - 0.38 ce qui donne ( cos a/2 ) = -0.38 ) une rotation de 224° ou -224° qui correspond bien (à 360° près ) aux 138° précédents.
L'idée vient de la constatation qu'avec la régulation de Laurens, dans le cas idéal le nanosatellite est arrêté fixe dans le repère de consigne, et qu'une rotation autour du vecteur B ou de l'axe du quaternion suffit à retrouver le repère de consigne ( pour nous R0 )
Donc je garde la régulation boussole et je remplace la régulation parallèle ( pilotée par la fonction laurens3.m ) et j'essaye un contrôle des angles autour de B ( piloté par laurens4.m )
NB : Cette simulation n'a pas été programmée encore. En fait elle ressemble beaucoup à celle qui utilise l'angle de rotation du quaternion, ce qui semble plus en accord avec le contrôle d'attitude s'il est présent et utilisable.
1°) CE QUE DIT M LAURENS EN TOUT DEBUT DE SON BREVET :
|
Pour contrôler l'attitude d'un satellite placé sur une orbite terrestre basse on créée, à l'aide d'au moins trois magnéto-coupleurs (10,12,14), un moment magnétique M colinéaire à ce que serait une direction de consigne, constituée par la direction du champ géomagnétique en axes satellite si celui-ci était pointé de façon idéale, afin d'aligner de façon permanente la direction magnétique de consigne sur la direction magnétique courante et on contrôle la position angulaire autour de la direction magnétique courante instantanée (b) par un moment cinétique. Pour amortir le contrôle, on génère un moment magnétique M total de valeur vectorielle:
où K et D sont des gains, b est le champ magnétique terrestre réel local et B est le module de ce champ. |
NB1 : On reconnaît en rose la régulation boussole, en rouge M LAURENS préconise sans autre précision l'utilisation d'un moment cinétique supplémentaire pour contrôler la position angulaire autour de B.
NB2 : Les simulations précédentes montrent bien que les vitesses angulaires sont annulées mais que la position angulaire finale est aléatoire. En clair B et Bc sont confondus, mais R0 et R ne le sont pas, ce qui permet de dire que R se déduit de R0 par une rotation autour de B.
2°) ESSAI DE MISE EN PLACE D'UN MOMENT CINETIQUE COMPLEMENTAIRE :
L'origine de ce moment cinétique ne peut être qu'une roue, que nous avons prévue suivant l'axe y du satellite qui devrait venir coïncider, en fin de régulation, avec Y du repère orbital.
Le problème est que nous devons créer un couple C porté par l'axe de B, alors que la roue donne un couple Cr sur y, il faut donc compléter, avec les magnétocoupleurs, par un couple Cm tel que vectoriellement on ait :
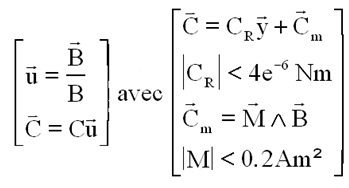
3°) CALCUL DES COUPLES A GENERER :
La figure montre les éléments essentiels des calculs reliant C, Cr et M. Cm est obligatoirement orthogonal à B.

Il nous faut évaluer le moment magnétique M nécessaire pour créer Cm.

Comme Cm est orthogonal à B, il vient :
![]()
Ce qui permet de calculer le moment magnétique à générer

4°) CHOIX DE LA LOI DE REGULATION Cr :
Dans un premier temps, on évalue l'écart angulaire, autour de B, entre le repère de consigne R0 et celui du satellite R qui devrait rejoindre R0.
Cet angle est accessible par le quaternion d'attitude Q, qui tend vers la représentation d'une rotation autour de B, ou encore de l'axe u unitaire de la rotation ou encore l'unitaire de B, du moins en fin de la régulation boussole de Laurens. Ce point a été vérifié sur les simulations précédentes.
a) Récupération de l'angle :
Par la première composante de Q soit Q(1) = cos ( b / 2 ), donnant b.
b) Commande du couple roue en PD :

NB : Le couple C apparaît comme un contrôle proportionnel-dérivé à gain variable.
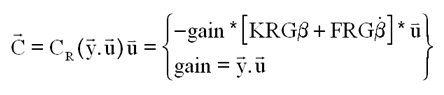
avec une contrepartie, à savoir que la régulation est moins efficace quand l'axe de tangage approche de sa position nominale.
c) Calcul du moment magnétique M :

Ce moment magnétique vient se rajouter à celui de la régulation boussole, qui est maintenant bien réduit, car les vitesses angulaires sont faibles et Bc très près de B.
d) Plafonnement proportionnel classique des moments magnétiques et du couple roue :
Il est appliqué pour toutes les régulations et concerne simultanément le couple roue et les moments magnétiques, quand tout fonctionne en parallèle.
*************************** Fin de page ****************************