La mise en spin autour de la normale aux panneaux semble, pour moi,  un échec. Je  reprends donc une ancienne régulation de Laurens et Damilano, qui réalisait le "détumbling" puis la mise en spin autour d'un axe choisi, à une vitesse angulaire également choisie,  pour comparer les résultats avec la méthode de précession de Steyn. Cette fois, l'axe de spin est l'unitaire soleil.

Deux simulations sont exécutées, avec ou sans roue à vitesse constante.

I DESCRIPTION ET RESULTATS DE LA SIMULATION LA PLUS SIMPLE ( sans roue ):

C:/casasurv/laurspin/SurvSpin.m initialisée par surv2dat.m

1°) La loi de commande en 2 temps :  H=21 h 30, pas de roue, jour =183 ( voisin du solstice d'été )

a) Premier temps : de 0 à 1500 s, la plus simple des régulations en B-dot, avec K=600000 SI

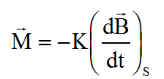
a) Deuxième temps : de 1500 s à 30000 s ( 5 orbites ), la régulation en B-dot complétée par la mise en spin autour de la direction pointant le soleil, avec toujours  K=600000 SI. La vitesse angulaire de mise en spin de l'exemple est de 2.5 °/s.

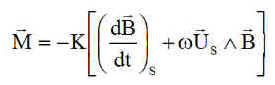
La simulation commence à mesurer l'énergie produite, à parti de 5000 secondes, de manière à avoir un régime stabilisé et une excellente idée de la puissance moyenne.

Optimisation du moment et respect des limites physiques ( rappels ):

1 - Seule, la composante du moment magnétique normale au champ est conservée:

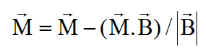
2- Pour parer à la saturation :

2°) Les vitesses angulaires : 

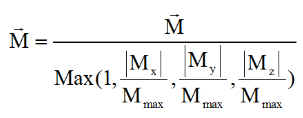
Une fois amorti le "tumbling" initial ( faible sur l'exemple ), la stabilisation est parfaite. La vitesse de tangage est celle du spin à 2.5°/s en résonance classique avec le champ magnétique terrestre à une période de 3000 secondes.

a) Nutation transverse :

On note une très petite nutation transversale.

min(p2plusr2(10000:15007))*180/pi=0.15 °/s  et   max(p2plusr2(10000:15007))*180/pi=0.23 °/s, fournissant une vitesse moyenne transverse de 0.19 °/s

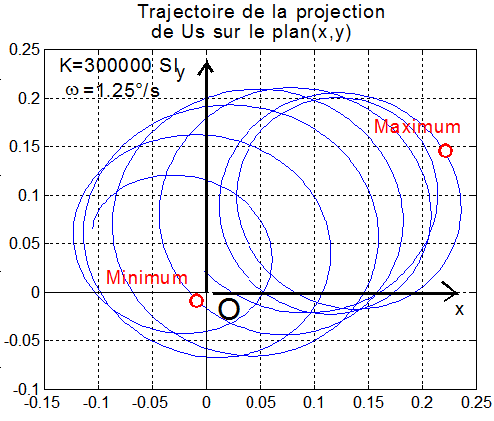
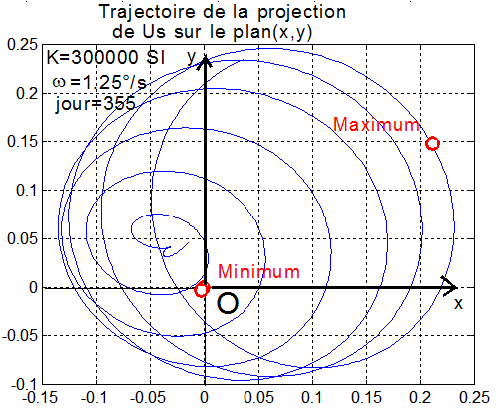
1 - Ci-dessous trajectoire de la projection de Us unitaire soleil, dans le plan satellite (x,y)

Projection de toute la trajectoire de la projection de Us sur (x,y)

Projection de la phase finale de la trajectoire de la projection de Us sur (x,y)

2 -Décalage angulaire entre l'axe -y et l'unitaire soleil : 

L'axe -y s'éloigne au maximum de la direction du soleil de 8°.4

max(acos(-Us(10000:15000,2)))*180/pi = 8°.4    min(acos(-Us(10000:15000,2)))*180/pi = 0°.06

L'écart moyen est de l'ordre de 5 à 6°

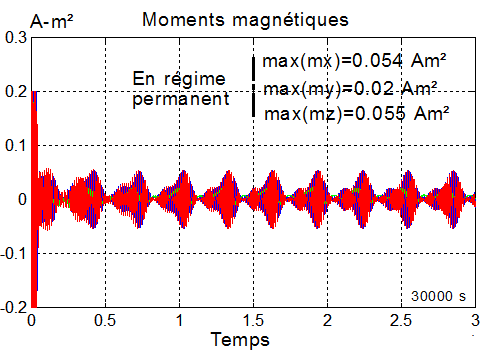
b) Moments magnétiques :

En régime permanent, aucun des 3 moments magnétiques ne dépasse 0.055 Am². La consommation électrique supposée être somme des 3 alimentations correspond au moment fictif M=|mx_deriv|+|my_deriv|+|mz_deriv| =  0.09 Am² , disons 0.1 Am² soit, pour cette simulation 50% du moment maximum, pour un seul magnétocoupleur. Conclusion à tirer???

3°) Energie produite :

Pour le jour 183 sensiblement au solstice d'été, la durée des éclipses est de 1955 s par période de 6074 secondes. Rappelons que la normale aux panneaux est inclinée de 35° sur l'axe - y. 

Le graphe de l'angle entre l'axe - y et Us direction unitaire du soleil, donne un écart moyen d'environ 5 à 6°.

La puissance minimale moyenne sur une orbite, est donc sensiblement ( pire cas )

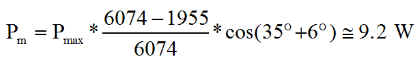
C'est bien la valeur enregistrée par la simulation, après le temps de stabilisation de 5000 secondes. Ce niveau d'énergie est tout à fait acceptable.

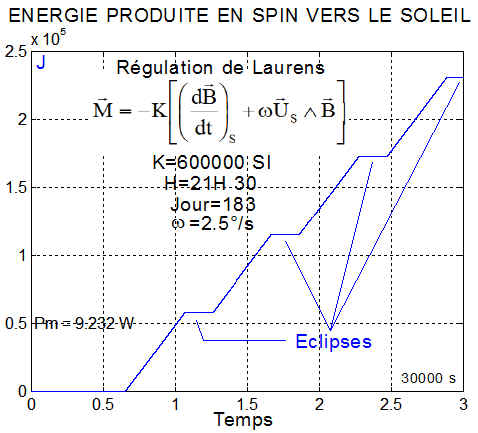
4°) Commentaires :

- Un essai avec un spin divisé par 5, donne bien une stabilisation, mais sur un temps plus long et une production moindre d'énergie.

- Un essai avec un spin divisé par 2, donne bien une bonne stabilisation, mais sur un temps analogue et une production légèrement moindre moindre d'énergie à puissance moyenne 9 W, donc tout à fait acceptable. La consommation des magnétocoupleurs est bien diminuée.

- Avec le spin initial, mais le gain K de 600000 divisé par 2, le résultat est tout aussi excellent avec une puissance moyenne de 9.37 W et bien sûr une consommation moindre des magnétocoupleurs ( divisée par 2, de l'ordre de 0.05A-m² )

CONCLUSIONS

- Enfin pour terminer avec un spin divisé par 2 et un gain divisé par 2, les résultas sont tout aussi acceptables car :

* Comme le montre la figure ci-dessous, le spin est moins décentré qu'avec la simulation principale

* La puissance moyenne n'est que très faiblement impactée 9.19 W au lieu de 9.232 W, soit une diminution de 0.4%, insignifiante.

* Les  magnétocoupleurs travaillent en régime permanent, comme une seule bobine de moment 0.02 A-m² donc à 10% des capacités maximales.

Le cas le plus favorable est le solstice d'hiver : le graphe montre un meilleur enveloppement du spin autour de - y. 

Le gain de puissance est très net avec Pm = 9.76 W

II PRECAUTION A PRENDRE : citation de Laurens qui va orienter la suite, même si ce n'est pas exactement la même stabilisation

1°) Question en suspens :

Les simulations fonctionnent parfaitement, et le satellite s'est toujours retrouvé toujours "spinné" autour de - y orienté vers le soleil. Ce qui est le but.

Mais comment la régulation sait-elle que c'est -y qu'on aligne sur Us avec une vitesse de spin < 0 et pas y sur -Us avec une vitesse de spin > 0, auquel cas les panneaux ne seraient pas éclairés??? 

En effet, la régulation ne connaît que le produit w_spin*Us .

Cette question me taraude l'esprit depuis le début de cette nouvelle étude !!! Faut-il prendre des précautions?

2°) Réponse provisoire mais non satisfaisante:

J'ai constaté que si les conditions initiales sont notamment proches de la configuration de pointage nadir,  alors l'alignement de - y sur Us se produisait à chaque fois. 

Conclusion: Je suis le conseil de M Laurens : utiliser la roue sur l'axe y, à vitesse constante, de spin négatif, pour permettre l'alignement de l'axe - y sur le spin de Laurens.

III NOUVELLE SIMULATION AVEC UNE ROUE ( à vitesse constante ) :

C:/casasurv/laurspin/Surv_L_R.m initialisée par surv2dat.m

( A noter qu'on peut passer de la seconde simulation, à la première en faisant K_roue = 0 dans surv2dat.m )

H=21 h 30    jour = 355 ( solstice d'hiver ) K=300000 SI   w_spin=1.25°/s

On utilise la roue qui est disponible dans toutes les simulations déjà testées, à vitesse constante, sur l'axe +y, simplement en vitesse de rotation négative, pour assurer en régime normal la stabilité du pointage nadir. Un module de couplage avec les vitesses satellite a simplement été ajouté à la simulation précédente ( il est de plus en option ).

La loi de régulation reste la même : au départ la loi B-dot

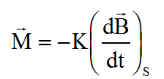
Puis de 1500 s à 30000 s ( 5 orbites ), la régulation en B-dot complétée par la mise en spin autour de la direction pointant le soleil, avec K=300000 SI. La vitesse angulaire de l'exemple est w = 1.25 °/s.

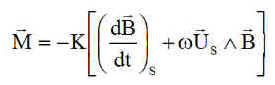
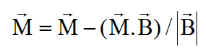
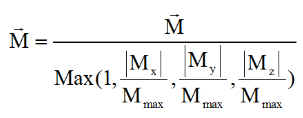
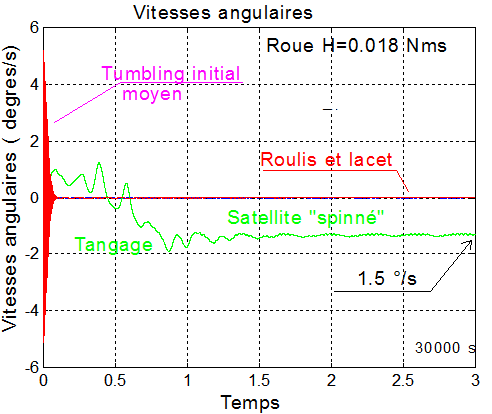
1°) Vitesses angulaires : 

Exemple avec au départ des vitesses angulaires moyennes, roue en fonctionnement continu de moment cinétique H=0.018 Nms ce qui correspond à une roue BCT à 666 tours/mn ou une roue BCT Micro Réaction à 6000 tours/mn

% Initialisation en vitesses (rd/s)  v_roulis0=0.06; v_tangage0=-0.05; v_lacet0=0.01;  % Initialisation en position (rd)  roulis0=0.1; tangage0=0.1; lacet0=0.05;

2°) La qualité du pointage soleil : 

2 graphes montrent le résultat, avec la projection sur le plan satellite ( x,y ) de l'extrémité du vecteur Us unitaire qui pointe le soleil. 

Le premier est la trajectoire complète depuis le début de la simulation. Le deuxième représente une partie seulement de la fin de la phase stabilisée ( c'est l'équivalent du trou central et de sa bordure dans le premier )

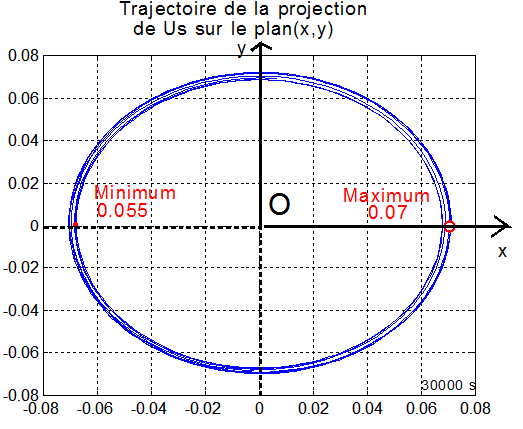
Commentaires : 

1 - les festons représentent le couplage de la roue avec la vitesse de tangage qui s'amortit de plus en plus.

2 -  la partie centrale très dense est la phase terminale.

3 - le graphique 2 donne les rayons extrêmes Rmax=0.07  et Rmin=0.055 des cercles. Il suffit d'imaginer que le cercle moyen est la projection du cône décrit par Us pour avoir immédiatement les dépointages limites angulaires y de l'axe - y par rapport à Us.

arctg(0.0055) < y  < arctg(0.007)  ==>   3° < y  <  4°   ==>  Le pointage est parfait, 

4- On voit donc clairement, en comparant les trajectoires avec et sans roue, une nette amélioration du pointage et de l'énergie. 

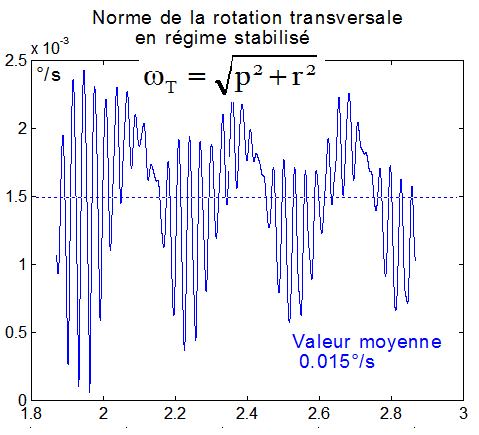
5 - Enfin, la nutation parasite devient insignifiante de l'ordre de 0.015 °/s comme vu ci-dessous entre les temps 18000 et 30000 secondes.

3°) Energie produite :

a) Puissance : En régime stabilisé vers le soleil, la puissance varie, au rythme de la faible nutation, autour de 14.6 W, ce qui donne compte tenu des éclipses, une puissance moyenne de 9.9 W, au dessus du niveau espéré. Nous sommes bien aux 2/3 de la puissance maxi, on ne pourra pas avoir mieux.

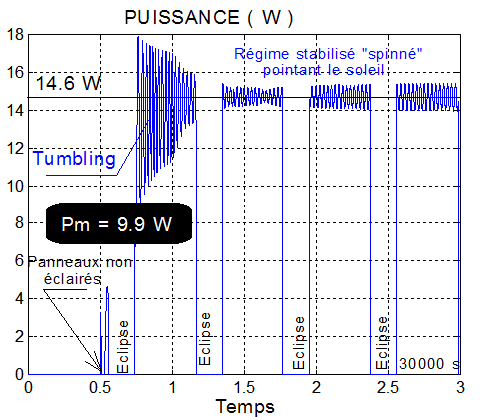
b) Energie : La puissance est confirmée par la courbe de l'énergie, mesurée depuis le temps 5000 s

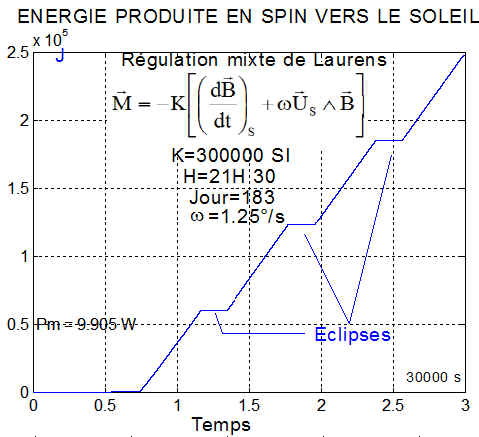
La formule de l'énergie devient, avec Pmax = 18 W, durée d'éclipse(jour 355) = 1825 s, période=6074 s et offset de 3.5° pour la normale aux panneaux, par rapport aux 35° d'inclinaison, pour le pire cas.

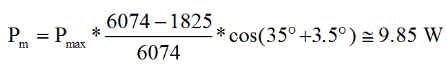
Confirmant en tous points les calculs et la simulation.

4°) Moments magnétiques : en phase stabilisée de survie, l'énergie consommée équivaut à celle d'un seul magnétocoupleur de moment 0.02 A-m², ce qui est très faible.

**********************************************

ANNEXES: FONCTIONS UTILISEES

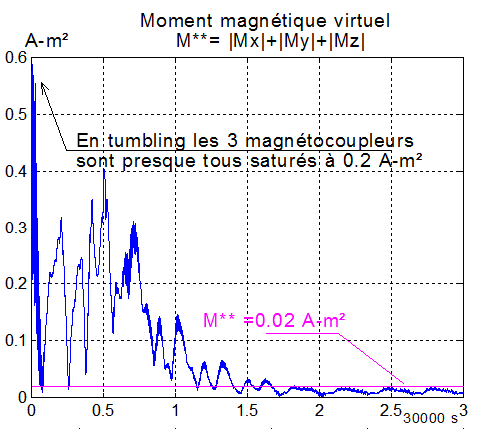
- soleil.m : fonction du temps, retourne 0 ou 1 en éclipse ou hors éclipse. Paramètres H (heure solaire) jour ( N° du jour de l'année )

- SunitXYZ.m : fonction du temps, retourne L'unitaire du soleil, dans le repère orbital Ro = ( XYZ ). Paramètres H (heure solaire) jour ( N° du jour de l'année )

- unitSxyz.m : fonction du temps et qu quaternion d'attitude, retourne L'unitaire du soleil, dans le repère satellite R = ( xyz ). Paramètres H (heure solaire) jour ( N° du jour de l'année )

- Unit_Sat.m : retourne l'unitaire soleil dans le repère satellite, ceci pour les calculs d'énergie des panneaux solaires. Le vecteur d'entrée est :

u est le vecteur d'entrée à 10 composantes:
u(1:3) = Us unitaire soleil en repère orbital R0
u(4:6) =Omega rotation absolue en axes satellite R
u(7;10) est le quaternion d'attitude du satellite  xyz / XYZ repère orbital

- verifica.m : programme de vérifications, sur un instant quelconque de la simulation nanosim.m , de tout type de transformation matricielle ou vectorielle : OK

- momspin1.m : programmation de la loi en B-dot avec contrôle de saturation et utilisation de la seule composante du moment magnétique normale à B

- momspin3.m:  programmation de la loi mixte en B-dot et mise en spin, avec contrôle de saturation et utilisation de la seule composante du moment magnétique normale à B.

- jwrotot1.m : programmation du couplage roue-satellite

--------------------------------------------------------------------------------------

function y=momspin1(u);

global Kbpoint w_spin axe_spin H jour

% Le vecteur entrée est à 6 composantes
% u(1:3) est le vecteur dérivée champ magnétique B' ( B'x B'y B'z ) en axes satellite
% u(4:6) est le vecteur champ B (Bx By Bz en axes satellite
% Unit sera son vecteur unitaire

% La fonction retourne le moment magnétique mx my mz plafonné à 0.2 Am²

% Séparation des vecteurs B et B_prime
B_prime(1:3)=u(1:3);
B(1:3)=u(4:6);

% Calcul de la matrice du produit vectoriel de u avec B
Rot=[0 -axe_spin(3) axe_spin(2)
axe_spin(3) 0 -axe_spin(1)
-axe_spin(2) axe_spin(1) 0];

mt_mgn1=-Kbpoint*B_prime';                           % Loi en Bpoint de M Damilano

mt_mgn2=-Kbpoint*w_spin*Rot*B'; % Loi complémentaire avec la rotation de consigne
% de vitesse w_spin et d'axe spin axe_spin

mt_mgn=mt_mgn1+mt_mgn2;
mt_mgm=mt_mgm-(mt_mgm*B')/norm(B); % Optimisation du moment magnétique

% Pour éviter une saturation qui risque de bloquer une composante par rapport à une autre
% et donc de ne pas avoir le couple opposé à la rotation principale, je mets 
% une saturation anticipée proportionnelle, ce qui :
% Gardera le couple opposé à la rotation transversale
% Limitera le moment magnétique des bobines à 0.2 Am²

maxi=[abs(mt_mgn(1)),abs(mt_mgn(2)),abs(mt_mgn(3))];
test=max(maxi);
if test>=0.2
y=0.2*mt_mgn/test;
end

if test<0.2
y=mt_mgn;
end                                       % Fin du test

end    % Fin programme

--------------------------------------------------------------------------------------

function y=momspin3(u);

global Kbpoint w_spin H jour

% Le vecteur entrée est à 9 composantes
% u(1:3) est le vecteur dérivée champ magnétique B' ( B'x B'y B'z ) en axes satellite
% u(4:6) est le vecteur champ B (Bx By Bz en axes satellite
% u(7:9) est le vecteur Us unitaire soleil en axes satellite
% Unit sera son vecteur unitaire

% La fonction retourne le moment magnétique mx my mz plafonné à 0.2 Am²

% Séparation des vecteurs B et B_prime
B_prime(1:3)=u(1:3);
B(1:3)=u(4:6);
Us(1:3)=u(7:9);

% L'axe de spin est  l'unitaire soleil

axe_spin=Us;
% Calcul de la matrice du produit vectoriel de u avec B
Rot=[0 -axe_spin(3) axe_spin(2)
axe_spin(3) 0 -axe_spin(1)
-axe_spin(2) axe_spin(1) 0];

mt_mgn1=-Kbpoint*B_prime';                                  % Loi en Bpoint de M Damilano

mt_mgn2=-Kbpoint*w_spin*Rot*B';                        % Loi complémentaire avec la rotation de consigne de vitesse w_spin et d'axe axe_spin
mt_mgn=mt_mgn1+mt_mgn2;
mt_mgm=mt_mgm-(mt_mgm*B')/norm(B); % Optimisation du moment magnétique

% Pour éviter une saturation qui risque de bloquer une composante par rapport à une autre
% et donc de ne pas avoir le couple opposé à la rotation principale, je mets 
% une saturation anticipée proportionnelle, ce qui :
% Gardera le couple opposé à la rotation transversale
% Limitera le moment magnétique des bobines à 0.2 Am²

maxi=[abs(mt_mgn(1)),abs(mt_mgn(2)),abs(mt_mgn(3))];

test=max(maxi);
if test>=0.2
y=0.2*mt_mgn/test;
end

if test<0.2
y=mt_mgn;
end                                 % Fin du test

end

--------------------------------------------------------------------------------------

**************  FIN  **************

Cas d'une matrice d'inertie diagonale et de révolution autour de y.  L'énergie produite au solstice d'hiver est maximale et vaut 10.28 W

Si la matrice d'inertie est simplement diagonale, la puissance n'est guère plus petite, 10.22 W en moyenne.