|
REDUCTION DES VITESSES ET ACQUISITION DES ANGLES UNE SEULE REGULATION Méthode " boussole " de Philippe LAURENS |
![]()
|
Rédigé Avril-juillet 2014 I UNE STRATEGIE PARMI D'AUTRES IV CONCLUSIONS |
|
![]()
I UNE STRATEGIE PARMI D'AUTRES :
Après nombre d'essais de régulation, il est apparu qu'un moyen simple et fiable, consistait à opérer, soit en une seule régulation, soit éventuellement en 2 régulations consécutives:
1 - La réduction des vitesses ( dissiper l'énergie de rotation ) par des magnétocoupleurs, générant un moment magnétique M, interagissant avec le champ magnétique local B pour donner un couple de commande sur le satellite.
- a) Soit avec une loi en Bpoint ( Celle de Monsieur Damilano )
- b) Soit par la méthode de Monsieur Philippe Laurens, à partir d'un champ magnétique de consigne, c'est cette méthode qui est choisie dans ce résumé.
2 - Opérer l'acquisition des angles ( c,a,d les ramener aux valeurs de consigne, pour nous nulles ) :
- a) La loi en Bpoint de Monsieur Damilano, réduit parfaitement les vitesses, mais oblige à une autre régulation pour l'acquisition des angles
- b) Dans le cas de la régulation de Laurens l'acquisition se fait seule, probablement ( conclusion non encore prouvée ) grâce au moment cinétique de la roue.
II LA REGULATION TESTEE → 1 b) seule ( méthode Laurens ):
1°) SITUATION : Pour ma gouverne, répertoire NANOLAUR / NANOSIM0.M ou NANOSIM3 initialisée par NANODAT0.M
J'ai choisi des conditions extrêmes, à savoir grands angles initiaux et grandes vitesses sur les 3 angles de Cardan. En pratique, le tumbling et le retournement incessant du satellite, font que le choix des angles est certainement sans grande importance, seul le niveau des vitesses affectera la durée de l'acquisition.
% Initialisation en
vitesses (rd/s)
v_roulis0=0.24 rd/s; v_tangage0=0.2 rd/s
; v_lacet0=0.04 rd/s;
Ce sont des niveaux de l'ordre de 15°/s sur chaque angle et plus
globalement
% Initialisation en position
(rd)
roulis0
=1.3 rd ; lacet0 = -1.5 rd ; tangage0 = 1.4 rd;
vitesse roue = 100 rd/s; ce qui correspond quasiment à 1000 tours/mn.
a) Dissipation d'énergie : dans tous les cas, le technique de dissipation d'énergie par utilisation de la dérivée du champ magnétique, est fiable, certaine et surtout donne d'excellents résultats avec peu de moyens.
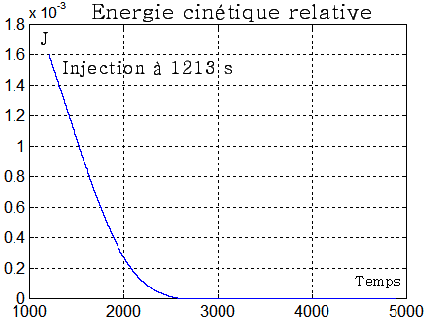
L'énergie cinétique décroît de manière très régulière à un taux de 1.6 e-5 J/s
Il est aussi très rassurant de voir, qu'avec ou sans roue, la décroissance de l'énergie est régulière, non affectée par la roue. Ceci tient au fait, qu'à vitesse constante, il n'y a pas de couple réactif ( pas d'accélération angulaire ) et que seul agit le couple gyroscopique de puissance nulle.
![]()
b) Evolution des angles : après un " tumbling " d'environ 1300 secondes suite à l'injection vers 1200 s, l'acquisition des angles s'opère en 2500 secondes. L'opération complète depuis le lancement aura duré un peu plus d'une heure. Elle débute un peu avant l'approche du pôle nord et se termine à mi-chemin du pôle sud et du premier survol de l'équateur.
On peut vérifier l'énergie initiale, avec en rouge les 3 vitesses absolues p q r :
Quelques lignes sur Matlab et la matrice d'initialisation etat_init= ( p q r + Q )
etat_init = [0.2597 0.0571 -0.1928 0.6184 0.4499 0.5243 -0.3745]
Energie=0.5*[0.2597 0.0571 -0.1928]*Asat*[0.2597 0.0571 -0.1928]' = 0.0016 J, c'est bien la valeur de départ du graphe
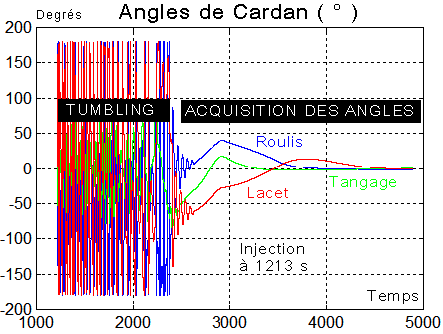
Le retour à 0 est régulier sur les 3 angles
c) Evolution des vitesses angulaires : un examen détaillé montre que le tangage a un comportement différent des 2 autres angles, la rotation absolue q tend d'ailleurs vers la rotation orbitale w0 de l'ordre de 0.001 rd/s
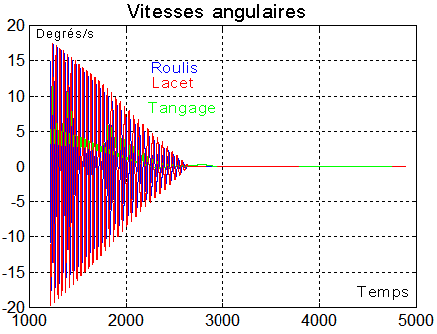
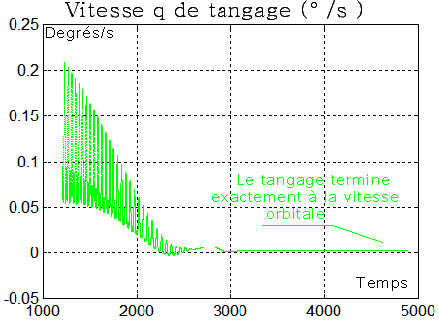
d) Suivi du quaternion : une fois le " tumbling " passé, la convergence de l'angle de rotation ( passage de R0 à R ), vers 0 confirme une acquisition correcte.
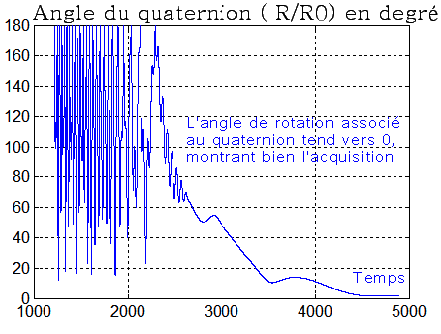
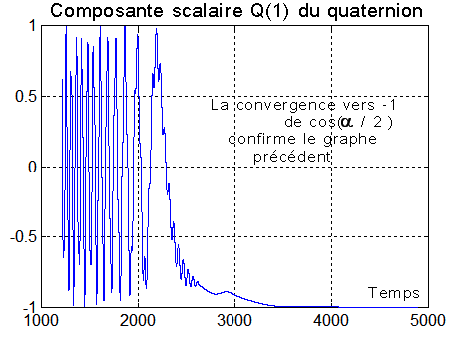
Ici la composante q1 du quaternion tend vers -1, signifiant que la moitié de l'angle de rotation vaut 180 °
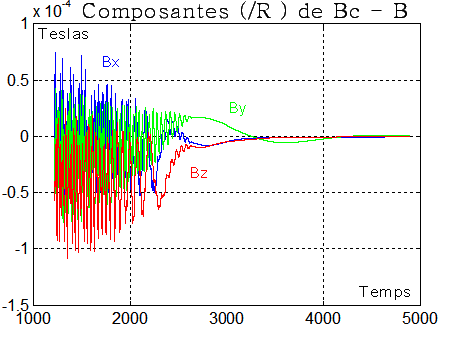
Autre confirmation avec le champ B qui se rapproche de sa consigne Bc, donc PB --> B
La roue de manière très générale, peut intervenir sur le satellite de 2 manières très différentes:
1 – Comme actuateur, sur commande, elle peut exercer un couple de réaction en fonction de la variation de vitesse imposée par un courant adéquat. C'est la fonction de pilotage réactif par échange de moment cinétique entre la roue et le satellite. Ce type d'action, pour une commande totale, doit utiliser 3 roues de réaction. Ce ne sera pas le cas dans la régulation de Laurens la plus simple.
2 – De manière tout à fait normale, mais moins évidente, même à vitesse constante, elle génère une réaction gyroscopique, par couplage de sa vitesse avec celle du satellite, réaction d'autant plus importante que la vitesse est grande. Comme la roue est sur l'axe de tangage, ce couplage s'exprime sur les axes roulis et lacet.
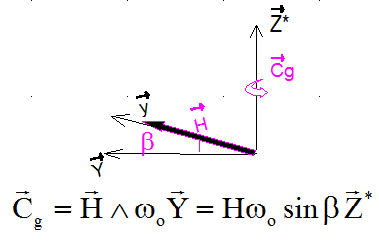
Si l'axe y s'écarte d'un angle b de la direction Y normale au plan orbital et si H , moment cinétique de la roue est positif, sous l'effet de la rotation orbitale, la roue réagit en imposant au satellite un couple gyroscopique Cg qui tend à rapprocher y de Y. C'est la fameuse propriété d'alignement des axes de rotation gyro sur la rotation imposée par le support de l'axe gyro ( ici le satellite et sa rotation orbitale ).
Le graphe montre le couplage roue satellite
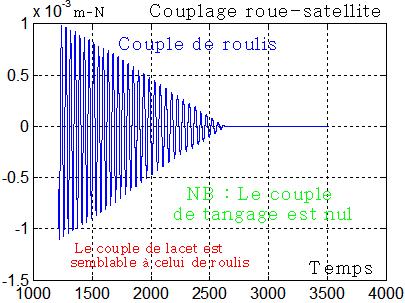
Le graphe confirme la valeur calculée de 0,001 mN
Faisons d'abord un calcul sommaire moyen, avec une inertie roue de J = 3,2 e-5 m²kg, une vitesse roue pour cette simulation de Wr = 100 rd/s et une vitesse angulaire satellite de l'ordre de w = 0,3 rd/s. La norme du couple est de l'ordre de C = J Wr w = 3,2 e-5 * 100 * 0,3 = 0,001 mN
On constate que ce couple, du moins en début de "tumbling", est bien supérieur au couple que pourrait délivrer cette roue sur commande ( 4 e-6 mN )
A retenir que seul le moment cinétique H=J W est seul utile à connaître pour la suite
NB : Peut-être faudra-t-il réfléchir au choix de la roue et de la vitesse nominale choisie en tumbling, pour que la roue travaille dans les meilleures conditions possibles.
Il faut aussi se poser la question, du lancement en rotation de cette roue, avant ou après l'injection? Car après, il y a un risque ( à étudier ) de déstabilisation qui se rajoute aux autres péripéties du lancement.
La roue suivante (The BCT Micro Reaction Wheel is a highly capable CubeSat sized Reaction Wheel.)

De caractéristiques

La simulation est prévue implicitement pour le moment cinétique H = 0.0032 mNs, utilisé depuis le début de mes travaux. Il suffit de cliquer 1 ( initialisation ). Cependant, en cliquant d'abord en 1, puis sur 2 on peut essayer la valeur du clic 2. On peut alors tester les 3 types de roues sur une même simulation écourtée ( pour gagner du temps ), en prenant des vitesses initiales raisonnables ( sinon je dépasse les capacités mémoire )

Voir le courbes en annexe
5°) SYNTHÈSE DES PRINCIPAUX RÉSULTATS : programme display.m
PRINCIPALES DONNEES DE LA SIMULATION
Nanosatellite nanolaur/regboux7.m initialisée par laurdat0.m
**************************************************************
Latitude d'injection = 70 °
Heure d'injection = 1213 s Avec rappel convention --> Heure =0 s au survol équateur
Heure de fin de Tumbling = 5002 s, soit 3789 s, après l'injection
--------------------- RESPECT DES SPÉCIFICATIONS ------------------------
Moment magnétique maximum bobine = 0.2 Am²
Vitesse angulaire de coupure en fin d'acquisition detumbling = 0.002 rd/s
Ecart maximum de pointage en acquisition fine = 5 °
Ecart angulaire maximum toléré sur le quaternion = 10 °
Couple maximum sur la roue = 4e-006 Nm
Nombre minimum de points stockés pour les courbes = 4e+004
Consigne de tangage = 0 rd
Consigne de roulis = 0 rd
Consigne de lacet = 0 rd
Simulation avec champ pulsé
Période des mesures = 5 s
Durée de la mesure = 0.1 s
--------------------- COEFFICIENTS DE LA REGULATION ------------------------
Régulation de type PD de Laurens avec champ magnétique de consigne
KPD_laurens= 0.000016 SI, pour le rappel proportionnel
FPD_laurens= 0.0084 SI, pour l'amortissement sur la dérivée
NB : Les coefficients peuvent etre modifiés dans le module dédié de la simulation
ou directement dans l'espace Matlab
--------------------- VALEURS INITIALES ------------------------
Angle de roulis = 1.3 rd Vitesse de roulis = 0.24 rd/s
Angle de tangage = 1.4 rd Vitesse de tangage = 0.2 rd/s
Angle de lacet = 0.05 rd Vitesse de lacet = 0.02 rd/s
--------------------- FONCTIONNEMENT DE LA ROUE ------------------------
Inertie de la roue J_ROUE= 0.000032 m²kg
Vitesse initiale = 100 rd/s ou 954.9 tours/s
Vitesse finale = 93.14 rd/s ou 889.4 tours/mn
Rotation maximale = 360 rd/s ou 954.9 tours/s
--------------------- RAPPEL DES CONDITIONS INITIALES ------------------------
Vecteur à 7 composantes initialisant l'intégration par le quaternion d'attitude en repère orbital
etat_init = [0.2597 0.0571 -0.1928 0.6184 0.4499 0.5243 -0.3745]
Rotation absolue initiale en repère satellite: p=u(1) q=u(2) r=u(3)
Quaternion d'attitude initiale par rapport au repère orbital:Q =[u(4) u(5) u(6) u(7)]
************** FIN DES SORTIES ****************
Le Stop de la simulation est commandé par 3 conditions simultanées ( fonction AND ):
1 - Angles < à un minimum fixé plus haut
2 - Angle de rotation du quaternion < à une valeur précisée plus haut
3 - Vitesses angulaires inférieures à un seuil prédéterminé
Ces seuils peuvent être supprimés ou adaptés suivant la mission
Idées formulées dans le désordre
1 - Faire vérifier par des étudiants ou autres personnes impliquées, que la simulation est bonne, robuste ( non sensibles aux conditions initiales …. )
2 - Tester de multiples combinaisons de constantes de la régulation, pour optimiser ces constantes et le temps d'acquisition.
3 - Définir les équipements nécessaires pour reproduire à bord les actions de cette simulation.
4 - Choisir la roue la mieux adaptée au problème.
5 - Vérifier si les niveaux de vitesses angulaires ( que j'ai choisi ) sont admissibles.
6 - Prévoir si une interruption est nécessaire pour une première ou d'ultérieures restitutions d'orbite. Si oui approximer leur durée.
7 – Simuler ( je vais commencer à y penser ) l'évolution moyenne des paramètres orbitaux sur 1 ou 2 ans, ceci pour justifier si une estimation de position et donc de champ magnétique reste correcte et acceptable dans le temps.
Une simulation de ce problème est certainement nécessaire pour vérifier que l'attitude reste « dans les clous »
8 – Introduire et tester l'introduction dans la simulation ( encore faut-il les estimer ) :
Des constantes de temps des systèmes de mesure
Des bruits, des biais, des erreurs de mesure …
Les contraintes des mesures ….
9 – Valider la simulation de la mesure du champ magnétique
10 – Prévoir le protocole de validation comparée de la simulation et des calculs qui seront effectués à bord
NB : Pour cette simulation, je n'ai pas modifié le couple max de la roue, vu que je ne me sers ( s'il n'y a pas d'erreur ) que de la vitesse et du moment cinétique. Une fois les choix faits, je mettrai à jour ces valeurs pour les autres régulations si nécessaire.
11 – Essayer de vérifier qu'en ramenant à 0 la vitesse de la roue, la stabilisation pose peut-être problème.
Il est précisé dans le brevet que le seul senseur à utiliser est un magnétomètre 3 axes qui fournit en axes satellite le champ magnétique avec une valeur proche de la valeur réelle mais entachée d'erreurs ( biais à corriger, erreur de mesure, bruit ). Cette valeur devrait être corrigée de manière à minimiser les erreurs (filtrage de Kalman?).
Une fois corrigées les composantes en axes satellite du champ magnétique local mesuré contribuent à la génération du couple de contrôle.
Un modèle théorique
de bord et une estimation initiale de la position du satellite sont
nécessaires. Le modèle de bord est un modèle
IGRF, dépendant des paramètres orbitaux. L'estimation
initiale de la position du satellite (donc des paramètres
orbitaux) permet une prédiction d'orbite et donc de position.
Il faudra
vraisemblablement recaler régulièrement le modèle
de bord avec l'évolution des paramètres orbitaux, la
fréquence étant à préciser.
Reste une question importante sur l'estimation des paramètres orbitaux sans propagateur d'orbite embarqué, probablement en lien avec la station sol (localisation par 3 visées optiques et transmission après calcul des paramètres orbitaux) .
( Considération personnelle )
Est-il nécessaire de prévoir une désaturation de la roue? Il me semble que non, car :
- La roue n'est utilisée qu'à vitesse constante.
- La régulation de Laurens semble assurer toutes les fonctions, depuis le détumbling jusqu'à l'acquisition et la régulation fine en régime de croisière, éventuellement entre des périodes de mouvements libres
Donc sauf besoin spécifique non prévu aujourd'hui, rien ne peut produire une saturation importante de la roue
Le seul critère de choix de la roue est son moment cinétique nominal H sous fonctionnement à la vitesse recommandée.
***********************************************
Fin de la partie importante du document
***********************************************
Renseignements personnels : La simulation NANOSIM0.M et son programme d'initialisation NANODAT0.M dérivent de REGBOUX7.M et LAURDAT.M
Annexes de comparaison des roues :
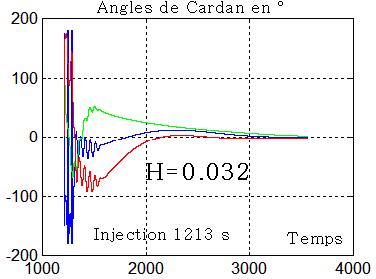
Ma roue à 1000 tours/mn
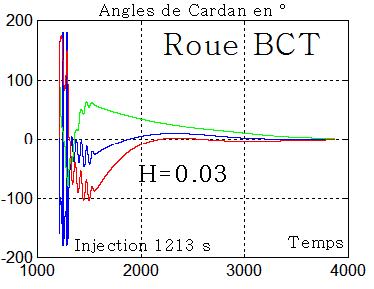
La roue BCT à 1000 tours/mn
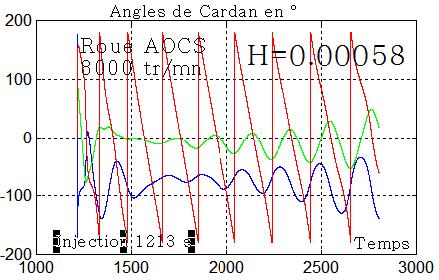
Acquisition impossible
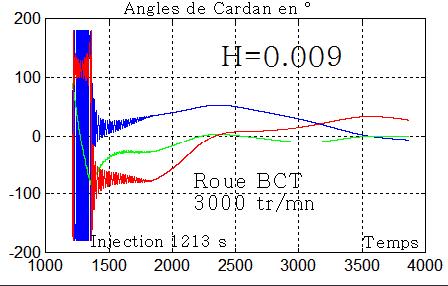
Acquisition longue incetaine molle
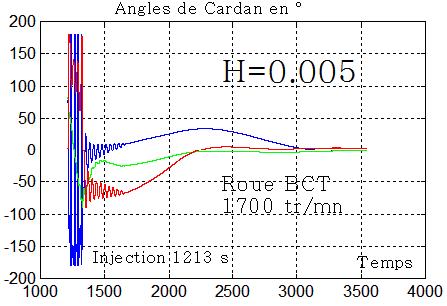
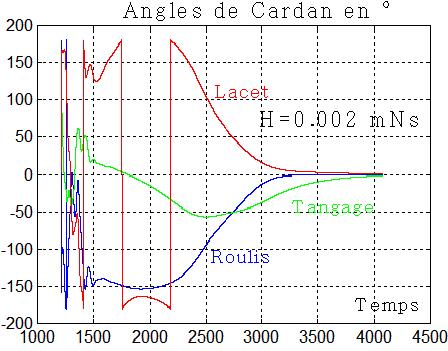
L'acquisition fonctionne
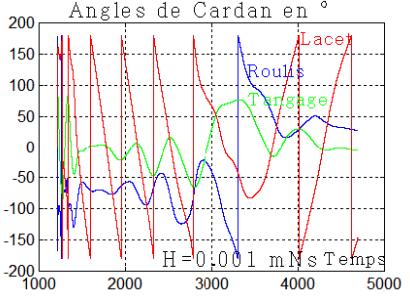
L'acquisition semble ne plus fonctionner , du moins dans les mêmes temps, mais ci-dessous en prolongeant la simulation, la convergence des angles est assurée
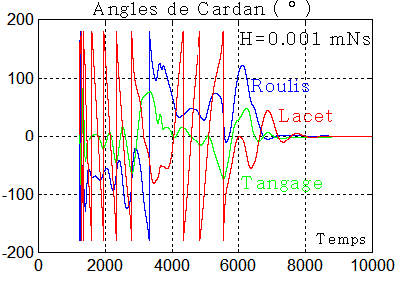
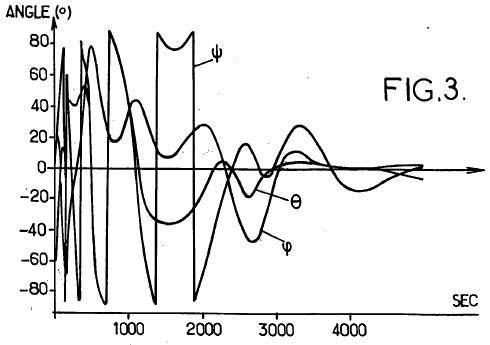
L'acquisition fonctionne 2 fois plus lentement qu'avec un moment cinétique double. Par contre, les angles reviennent par des oscillations amorties, un peu comme la figure donnée dans le brevet de M Philippe Laurens ci-dessous. Avec un retard orbital de 100 la convergence nécessite encore plus de 8000 secondes
Peut-être vais-je essayer une valeur moyenne H = 0.0015 mNs? Ci-dessous
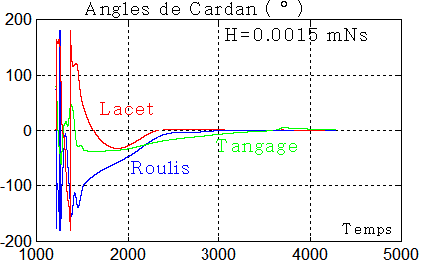
Conclusion : il semblerait que la plage admissible du moment cinétique de la roue soit de l'ordre de 0,001 à 0,005 mNs. La roue BCT a un moment cinétique nominal de 0,018 mNs, reste à voir si on peut le ramener sans dommages entre 0,002 0,005 mNs, c'est à dire travailler non pas à 6000 tours/mn mais entre 655 et 1666 tours/mn.
V QUELQUES ULTIMES VERIFICATIONS
A Satellite sans perturbations, roue arrêtée, pas de régulation: mouvements périodiques non amortis, l'énergie absolue se conserve. Une période est de l'ordre de 300 secondes.
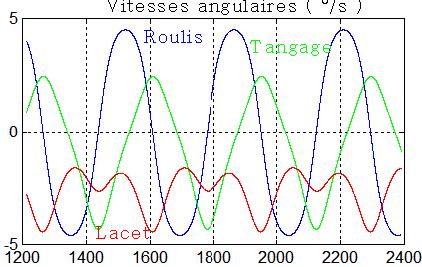
Satellite libre et conservatif
B Satellite sans perturbations, roue en rotation, sans régulation : l'énergie absolue se conserve, les mouvements sont périodiques, avec une période approximative de 49 secondes ( 16 périodes de 1213 s à 2000 s )
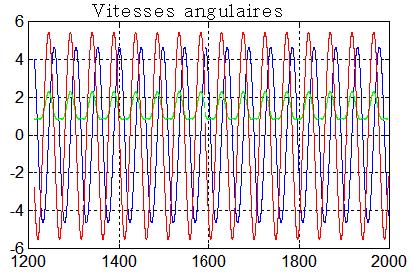
On peut retrouver la valeur de la période, en partant d'un satellite presque identique au nôtre, mais de matrice diagonale ( inerties A, B, C )
Les équations du mouvement de rotation en roulis et lacet, suite au couplage par la roue de moment cinétique H, sont
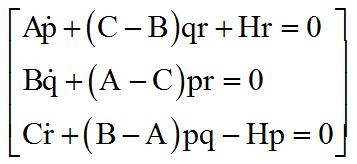
Les relations suivantes qui s'en déduisent, permettent d'éliminer les dérivées de r et de q
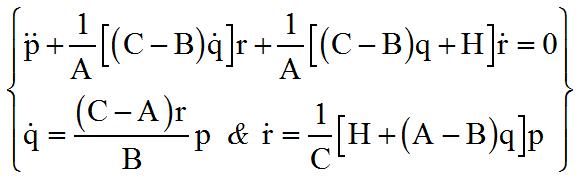
pour ne garder q'une seule équation avec comme variable principale p d'une équation ressemblant !!! à une équation classique, sauf que la pulsation est variable. Mais l'est-elle beaucoup? :
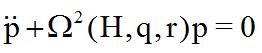
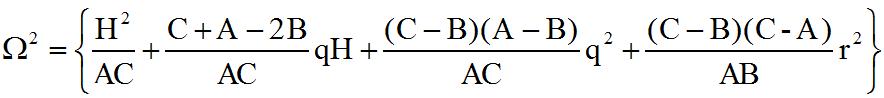
Numériquement nous obtenons :
![]()
Une fonction y=vibomega a été introduite pour calculer W. Son tracé montre que pour des vitesses initiales raisonnables comme celles faites plus haut, W pour ( H=0,0032 ) varie de 0,114 à 0,124, ce qui donne une valeur moyenne de 0,119, et donc sensiblement une période de 52,8 secondes, bien proche des 49 s trouvées plus haut.
Il est clair
que si H croît, W
tend vers
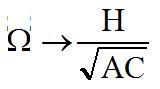
Par exemple
pour H = 0,005 mNs on a
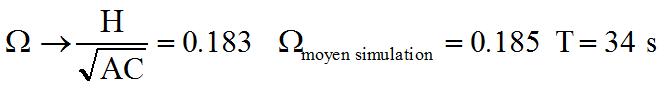
NB : Par contre je ne trouve pas encore d'explications au comportement différent du tangage.
C Satellite avec perturbations, roue en rotation, pas de régulation: Cas H=0,005 mNs
Les résultats ne sont pas affectés par les perturbations, car le couple de couplage est très nettement plus important que celui des perturbations. C'est une des qualités de la roue.
D Satellite avec perturbations, roue en rotation, avec régulation de Laurens: Cas H=0,005 mNs
Sans écrire les équations, les perturbations ne jouent pas de rôle, la régulation apporte des termes d'amoretissement traitant certainement la dérivée de p. La pseudo période reste la même.
CONCLUSION :
La roue fait disparaître l'effet des perturbations
sa rotation apporte un couplage stabilisant
en parallèle avec la régulation de Laurens.
Le diagramme de fonctionnement de la régulation est décrit ci-dessous :
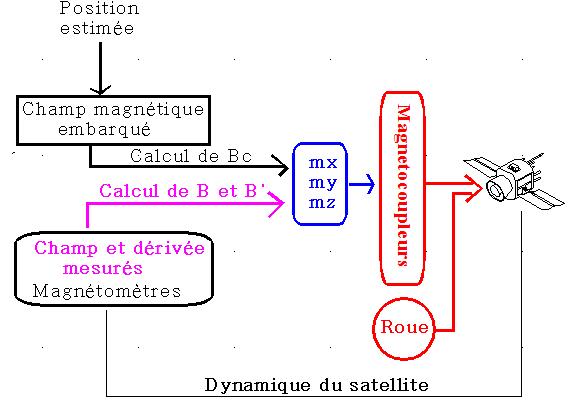
Le SCA nécessite :
- un modèle de champ magnétique embarqué, simplement alimenté par une estimation ou un calcul de la position.
- un magnétomètre 3 axes donnant champ etdérivée du champ en axes satellite
- 3 magnétomètres
- une roue fonctionnant à vitesse constante
Ce SCA n' a pas besoin de désaturation et assure :
- la réduction des vitesses après le lancement, en toutes conditions
- l'acquisition grossière puis fine des angles
- le contrôle du satellite en mode régulation fine
- il pourrait même reprendre en main le satellite après une mise en mode survie
2°) RAPPELS DES ELEMENTS DU CONTRÔLE :
1 – Une régulation de Laurens
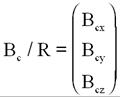
Champ de consigne donné par le modèle embarqué
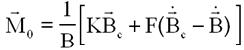
Calcul du moment magnétique brut, normalisé
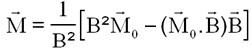
Calcul du moment magnétique optimal, avec seulement la partie normale à B
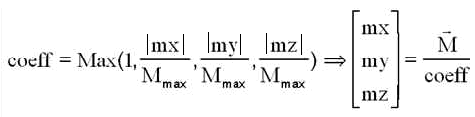
Calcul du moment magnétique efficace, utilisé
2 – Une roue à inertie de moment cinétique H dans la fourchette
0,002 mNs < H < 0,005 mNs
Les simulations ont montré :
1 - une faible sensibilité aux écarts de position
2 - un fonctionnement pour toutes conditions initiales
3 - la convergence vers la bonne position dans tous les cas
4 - une quasi insensibilité aux contraintes de la mesure, à savoir arrêt des magnétocoupleurs pendant la mesure du champ
4°) TEST D'ARRÊT DU CONTRÔLE FIN :
A ce jour, je n'ai pas encore trouvé de test fiable d'arrêt de la régulation, ce qui signifie pour moi qu'elle fonctionne en continu, sauf peut-être lors des survols de la station sol du suivi satellite ( transmission des mesures et des images )
5°) SYNTHESE DES SIMULATIONS : Voir la liste des simulations
NANOSIM0.M simulation de base, la meilleure solution
NANOSIM2.M simulation d'essai de plusieurs roues et de retards orbitaux de position, ce qui permettra le choix de la roue et une réflexion sur le suivi d'orbite.
NANOSIM4.M simulation avec toutes les sorties supprimées sauf angles et vitesses, ceci pour introduire des périodes de repos alternant avec des périodes de régulation. Pour mettre au point les constantes de temps.
NANOSIM5 simulation de séquences ' arrêt régulation ' suivies du ' mode libre sous perturbations '. La fonction utilisée est regulalt.m ( pour régulation alternée )
periode_sans ( par défaut 200 s ) est la période sans régulation
periode_reg =1000 s est la période du cycle donc 800 s avec régulation
******************** Fin de la page *********************