CONTROLE D'UN SATELLITE 

PAR ACTUATEURS ET REPERAGE DE CARDAN

Dans cette page, nous nous intéressons au contrôle d'attitude 3 angles, d'un satellite par 3 actuateurs au minimum, dans la mesure où 3 couples sont nécessaires :

- Magnétocoupleurs

- Roues de réaction

-Tuyères

-Gyroscopes

- etc....Nous ne parlerons que des 2 premiers,

Ces systèmes ont en commun d'être fixes dans la structure du satellite, et de produire chacun un couple modulable ( c'est le contrôle ) mais d'axe invariable lié au satellite.

Or ce qu'il faut contrôler, ce sont des angles ( qui donnent l'attitude ) et leur dérivées ( qui donnent l'évolution de cette attitude ). Ces angles sont mesurés autour d'axes, en général différents de ceux des actuateurs, l'effet des couples sur tel ou tel axe est donc dépendant de l'attitude quelquefois même au point d'être totalement inefficace ou de conduire à une situation singulière ( problèmes d'alignement ou de non définitions d'axes avec les angles d'Euler ou de Cardan par exemple). C'est une difficulté bien connue en gyroscopie.

L'objet de cette page est de préciser la gestion du contrôle. Nous nous limitons aux angles de Cardan en configuration quelconque.

I ELABORATION ET TRANSFORMATION DES COUPLES :

1°) Relations de transformation :

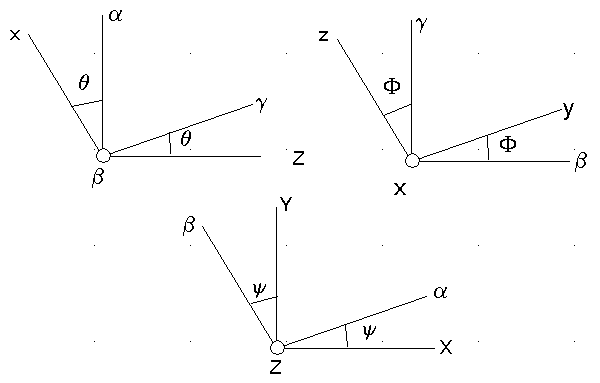
Le couple de contrôle à réaliser théoriquement ( si c'est possible ) est défini sur les axes dédiés aux angles. En effet c'est directement sur l'axe de mesure de chaque angle que la commande sera efficace, précise et sans "parasiter" les autres axes.

Le couple de contrôle est ainsi avec des notations évidentes ):

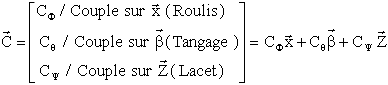
Le couple qui doit être physiquement physiquement réalisable est lui, généré dans les axes satellites portant les équipements. C'est le précédent transformé et exprimé dans les axes satellite.

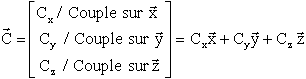
A première vue, on pourrait être tenté de dire qu'il est toujours réalisable de passer d'une expression à l'autre certes, avec les relations ci-dessous.

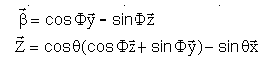
Ce qui conduit à une relation matricielle simple entre les 2 expressions du couple, utilisant la matrice P fonction des angles.

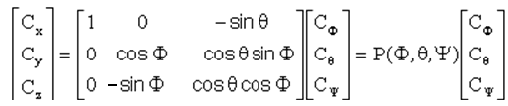
On notera que dans le cadre des petits mouvements ( angles de Cardan petits ), la matrice P est la matrice identité, le couple de commande en axes satellite et le couple spécifique sont égaux

C'est l'approximation opérée dans la régulation en pointage fin.

2°) LES DIFFICULTES APPARAISSENT :

a) Singularité mathématique :

Tout d'abord, il faut remarquer que le couple n'est réalisable physiquement que si les relations peuvent s'inverser. Ce qui suppose que la matrice P soit inversible. Or son déterminant vaut cosq.

Ce qui signifie dans cette configuration, et nous le savions, que si l'axe x est normal au plan (XY) la commande est impossible et surtout devient infinie ( les calculateurs n'aiment pas la division par 0 ), mais c'est surtout la non définition du lacet qui est responsable de la singularité qui est plus mathématique que physique.

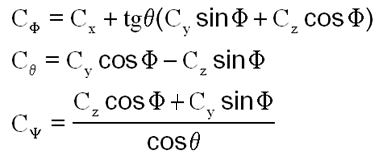
Solution : dans la simulation, il faudra donc mettre en sommeil la régulation lorsque le tangage s'approche de + ou - 90°. L'expérience confirmera si c'est nécessaire ou pas?

a) Singularité physiquede la commande par magnétocoupleurs:

Imaginons, et ce sera notre cas, trois magnétocoupleurs disposés sur les 3 axes x y z du satellite. Le moment magnétique M peut prendre toute valeur possible, mais avec le champ magnétique B existant à l'instant où nous parlons, il sera impossible de créer un couple magnétique parallèle à B ( nous le savions déjà ). Le croquis ci-dessous montre que le couple C est irréalisable avec le champ B, seul C2 est possible, mais pas la composante C1

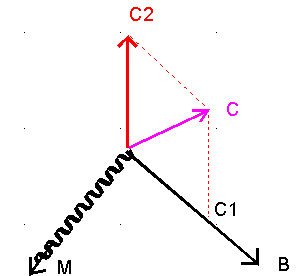
Ce qui est cependant rassurant c'est que la variabilité du champ magnétique le long de l'orbite permettra quand même un bon contrôle moyen.

II MISE EN PLACE D'UNE REGULATION :

Limitons nous à notre nanosatellite, dont nous voulons gérer l'attitude, notamment quand, après la mise en orbite,durant le " tumbling ", on réduit les vitesses angulaires, ce qui conduit le satellite dans une orientation presque inertielle ( sans vitesses ) mais de direction aléatoire.

Il nous faut alors le réorienter ce que nous appelons "ACQUISITION FINE". Une méthode consiste bien sûr à lui appliquer un couple judicieux, pour rétablir les angles sans trop donner de vitesses.

On comprend bien que pour être efficace, il faut traiter chaque angle par un couple particulier, naturellement orienté sur l'axe de mesure de cet angle. En clair par exemple pour le tangage q un couple de type PD

De même pour les 2 autres axes

1°) Avec 3 roues :

Trois roues disposées sur chacun des axes donnent chacune un couple Cr que nous pouvons calculer ( sauf au voisinage de  | q | = 90° par 

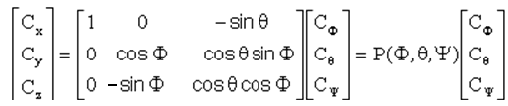
La commande opèrera sur la colonne de gauche. Mais nous n'avons pas 3 roues, seulement 3 magnétocoupleurs et une roue de tangage.

2°) Avec 3 magnétocoupleurs :

Nous partons du calcul du moment crée par un magnétocoupleur placé dans un champ magnétique de valeur locale B en axes satellite ( x y z )

Il faudrait calculer les moments magnétiques de telle manière que :

Cette écriture ne permet pas facilement de déduire les moments magnétiques respectifs de chaque bobine. Mettons la relation sous une forme matricielle plus explicite ( avec la représentation matricielle classique de l'opérateur calcul vectoriel ):

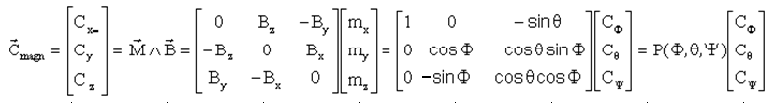
ou encore en notation matricielle

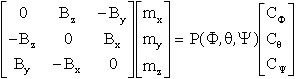
ATTENTION:

Premier écueil: Il est clair que le couple C imposé par les lois PID ou plus simplement PD, ne pourra jamais être colinéaire au champ B. Ce qui signifie qu'on ne peut pas appliquer de couple parallèle au champ magnétique, on est face à la singularité déjà signalée.

Deuxième écueil  : La matrice du champ a un déterminant nul, et n'est donc pas inversible. Le système ne peut avoir de solution que si C est orthogonal à B ( évidence au départ ), par contre cette écriture permet d'avancer pour la solution que nous cherchons.

3°) COMMANDE A 2 MAGNETOCOUPLEURS ( axe roulis & lacet ) + 1 ROUE SUR L'AXE TANGAGE

C'est la proposition retenue pour le nanosatellite. On libère un axe, pour nous celui du tangage, sur lequel on place une roue, commandée à part et pilotant le tangage, pour l'essentiel.

On souhaite commander chacun des 3 axes avec une loi de commande spécifique, dont le type peut être quelconque ( PID ou PD ou certains PID et d'autres PD etc...). Choisissons par exemple le type PID comme défini plus haut.

Donc on combine un couple de roue de réaction ( sur le tangage ) avec un couple magnétique sur les autres axes. Les bobines disposées sur les axes x et z donneront toujours un couple car le champ magnétique reste pratiquement dans le plan orbital, oscillant de l'axe Z vers l'axe X, tout au long de l'orbite.

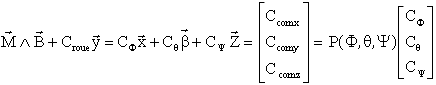
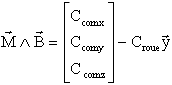
Cette équation admet pratiquement toujours une solution si le couple roue est bien choisi.

REMARQUE CAPITALE :

Le couple roue n'est présent que pour permettre de donner une solution au problème. En pratique, le couple roue supprimera notamment la composante du couple de commande dans l'axe du champ, ce qui permet le choix du moment magnétique. La roue n'est là que pour autoriser une solution, sa loi de commande est donc imprévisible et résultera des calculs à venir, cette loi sera calculée à chaque pas de temps.

CALCULS :

 mx et mz et Croue sont à déterminer ( connaissant B et le couple de commande en axes satellite ) avec la relation :

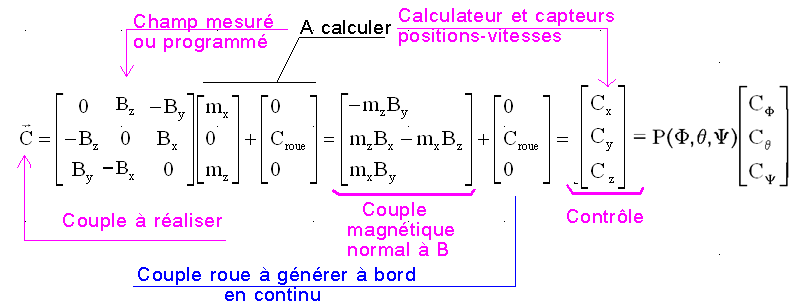
On peut écrire une relation équivalente :

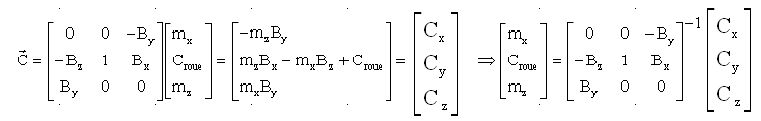
Maintenant, la matrice associée au champ B est inversible ( déterminant = B² y ( carré de la composante sur l'axe tangage ) composante qui n'est en général pas nulle sauf pour les configurations exceptionnelles ( à surveiller ) où l'axe y est normal au champ magnétique B.

La résolution directe donne ( en général ) des relations particulièrement simples:

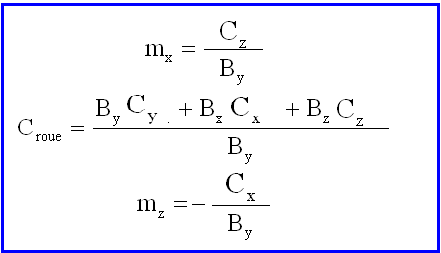
Vérifications :

La relation vue plus haut scalairement multipliée par B donne

Ce qui vérifie la valeur de C_roue. Les 2 autres relations résultent des projections sur les axes x et z.

Ces formules ne semblent plus poser de singularités, le long de l'orbite ( sauf au voisinage de q = + ou - 90° ). Cette manière d'utiliser le champ ne fera plus apparaître de composantes parasites sur les axes annexes à celui qui est contrôlé en principal.

NB1 : Tout à fait normalement, c'est mx avec Bz ou mz avec Bx qui contrôleront le tangage lors du survol du pôle ( resp  survol de l'équateur )

REGLE ET INTERPRETATION GEOMETRIQUE ( CONFIRMATION DES CALCULS ):

Reprenons la figure donnée plus haut et complétée ( proportions non nécessairement respectées )

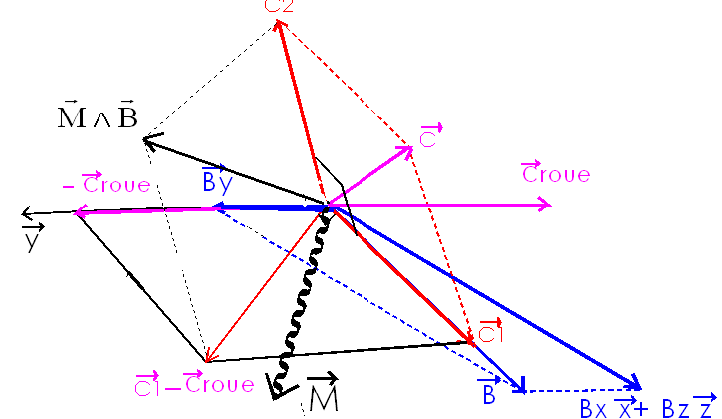
La figure montre que :

- On décompose C en C1 et C2 avec C1 sur B et C2 perpendiculaire à B ( opération toujours faisable )

- On décompose à nouveau C1 dans le plan (  y , B ) sur y et la perpendiculaire à B dans ce plan ( opération toujours faisable si la configuration y perpendiculaire à B ne se produit pas  )

.

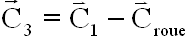
Ainsi le couple magnétique à générer est 

Le lecteur fera les calculs de projection qui donnent

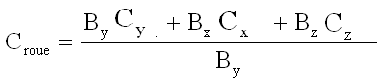
La relation s'interprète comme :

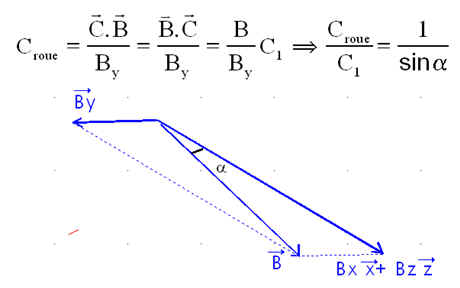
REMARQUE : De toute évidence, si l'axe de tangage y est normal au champ B ( By = 0 ), le calcul du couple roue est impossible. On note aussi que plus By est faible, plus le couple est grand.

REMARQUE A POSTERIORI :

C'est en relisant ce qui vient d'être écrit, que j'ai réalisé que l'on pouvait éventuellement s'affranchir de la division par la composante By, qui n'apparaît que comme l'inverse d'un gain pour les 3 PID. On pourrait donc choisir sans dommage les moments magnétiques suivants et le couple roue, puisqu'ils restent en proportionnels Cx Cy Cz:

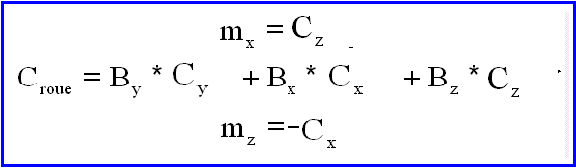
Cependant pour une orbite polaire, By est pratiquement nulle ou nulle suivant le modèle et donc il y aurait lieu d'étudier plus en détail la régulation. Comme ce n'est pas notre cas, je repousse à plus tard cette étude.

4°) Résultats de regderb5 :

Après avoir tâtonné pour le choix des bons gains, la simulation fonctionne et ramène, après le détumbling initial, les angles et les vitesses à 0, à peu près au même rythme. Un automaticien réalisera certainement une régulation plus harmonieuse !!!

Finalement pour le choix des paramètres de la régulation PD ou PID, j'ai essayé le raisonnement suivant:

1 - Considérant que durant l'acquisition, les perturbations sont très faibles devant les couples de commande, je ne prends en compte que ceux-ci.

2 - Dès que les angles deviennent inférieurs à 10°, en fin de simulation, les équations  deviennent linéaire du type :

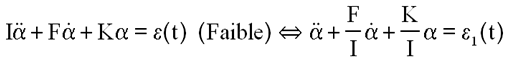
3 - Deux axes avec leur bobine, jouent des rôles identiques, le lacet et le roulis, aucun n'est plus particulier que l'autre. Seul le tangage est particulier, non pas géométriquement mais parce que régulé en plus avec une roue .

Donc, j'ai choisi au départ de les considérer comme devant être régulés au même rythme. Et pour simplifier, j'ai adopté le régime critique, quitte à m'en écarter un peu plus tard si nécessaire.

Je leur ai donc attribué les mêmes rapports F/I et K/I aux 3 axes. Les tâtonnements du début de l'étude m'ont conduit à choisir 

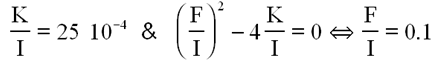
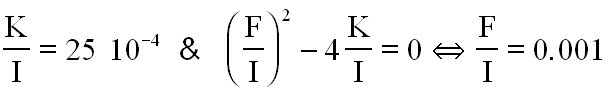
Aboutissant donc à une première approche suivant les axes et une première estimation des coefficients :

Données initiales : La simulation utilise des valeurs adaptées ( notamment pour le tangage durci en gain et amortissement ) de celles trouvées au dessus

NB : Des variations d'un coefficient 2 sur l'un des gains, ne changent pas la stabilité de manière visible, mais modifient notablement le résultat.

%***************** DONNEES PID ROULIS *************************

K_PID_ROULIS=8e-7; % Gain proportionnel
F_PID_ROULIS=1.6e-5*4; % Gain amortissement dérivée
gain_roulis=250000;

% ***************** DONNEES PID LACET **************************

K_PID_LACET=5.5e-7; % Gain proportionnel
F_PID_LACET=1.1e-5*4; % Gain amortissement dérivée
gain_lacet=380000;

% ***************** DONNEES PID TANGAGE ********************

K_PID_TANGAGE=9e-7; % Gain proportionnel
F_PID_TANGAGE=1.8e-5*4; % Gain amortissement dérivée
gain_tangage=330000;

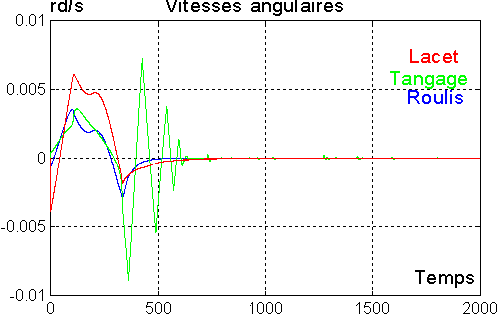
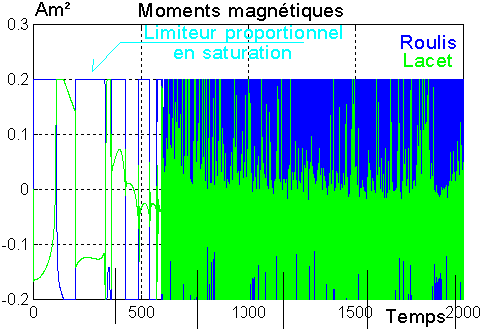
On note le respect des capacités des bobines à 0.2 Am²

Ci-dessous quelques détails

NB : On voit bien qu'un seul moment  à la fois est bloqué 

en saturation 

b) Une roue tangage + 2 bobines roulis tangage:

Une étude analogue donnerait

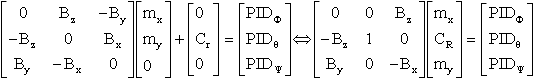
Là encore la matrice associée à B est inversible presque partout, car de déterminant By Bz, mais une singularité apparaît 2 fois par orbite, lors du survol de l'équateur.

Donnons quand même les formules des moments et couple roue à commander

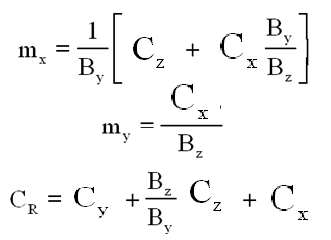
b) Une roue tangage + 2 bobines lacet tangage:

Donnons le résultat, avec toujours une singularité au survol des pôles

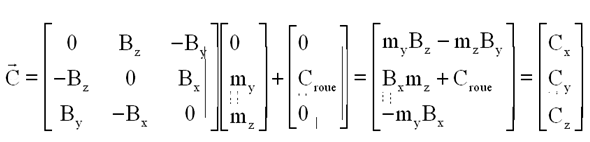
Relation équivalente au lien matriciel ( ne pas y voir  de composantes sur les axes!!! ) suivant:

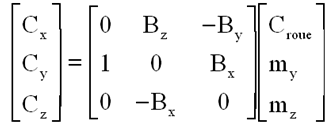
La matrice ainsi introduite a un déterminant Bx.By qui laisse supposer l'inversion possible partout où les 2 composantes ne sont pas nulles.

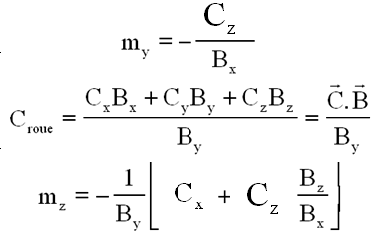
NB : Ces 2 dernières formulations seront peut-être tentées si la première ne fonctionne pas bien en acquisition, car elle a donné d'excellents résultats en mode petits angles.

Voir la régulation petits angles ou encore pointage fin

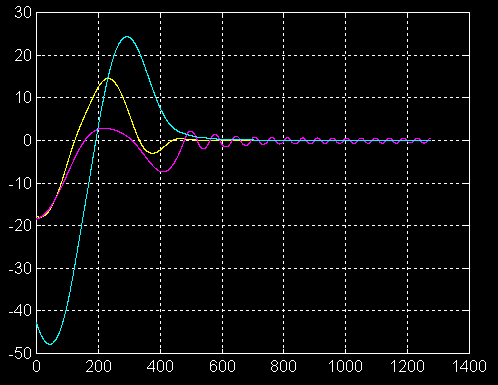
Une simulation perdue ??, celle qui donnait la meilleure allure 

de stabilisation. Jamais retrouvé les coefficients des PD

*************************  Fin de page **************************