RESULTATS DE MANOEUVRES DIVERSES
********************
Illustration des manœuvres classiques
********************
I SIMULATION PRINCIPALE NANOSIM0.M: initialisation dans nanodat0.m
But: aligner les axes satellites sur les axes du repère orbital avec y sur Y et pointage zénith ou -y sur Y et un pointage nadir Choix du type de pointage par la constante zenith ( 1 pour le zenith et -1 pour le nadir ), dans nanodat0 |
nanolaur/nanosim0 ou laursurv/nanosim0
Durée 10000 secondes; pas d'intégration = 0.4 s; précision 1e-3
1°) Roue : vitesse constante
J_ROUE=3.2e-5m²-kg
vitesseroue=100;
% Roue en début de régulation
rotation_initiale=100;
% Vitesse de rotation initiale de la roue 3600 t/mn
rotation_maximale= 360;
% Vitesse de rotation maximale de la roue environ 3600 t/mn
Hy=J_ROUE*vitesseroue;
% Moment cinétique de la roue sur l'axe satellite y.
2°) Gains de la régulation PD :
KPD_laurens=1.6e-5;
% Coefficient de rappel sur champ de consigne
FPD_laurens=8.4e-3;
% Coefficient de rappel sur dérivée du champ de consigne
2°) RESULTATS DE LA PREMIÈRE SIMULATION ( Pointage zénith ):
ZENITH=1
Repère de consigne XcYxZc = XYZ
Rotation > 0 de la roue autour de y
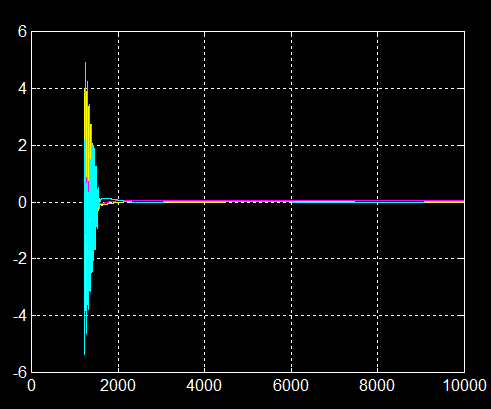
1° Vitesses angulaires : Le graphe des vitesses angulaires p q r dans les axes satellite, montre un amortissement parfait et des vitesses angulaires finales inférieures à 0.03 °/s, pour les 3 axes.

2°) Angles :
L'important est l'angle entre y et Y, que l'on devrait retrouver proche de 0°, ce qui est le but poursuivi.
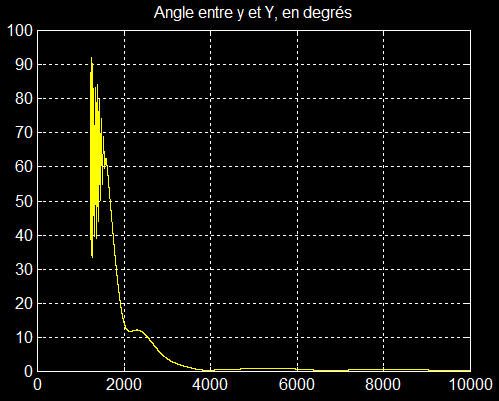
Stabilité confirmée par la coïncidence de x et X et donc aussi de y avec Y

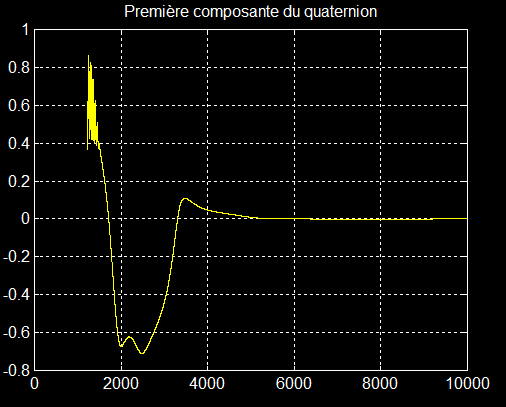
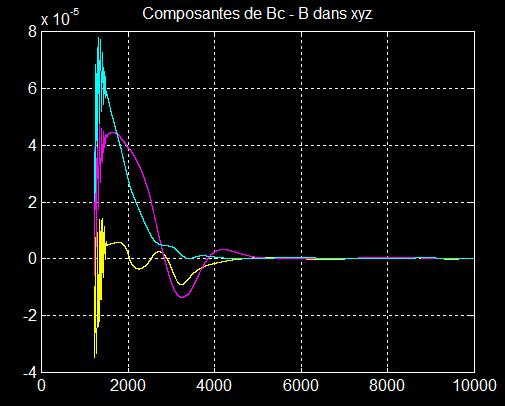
3°) Quaternion et attitude:
La comparaison des 2 graphes à partir de 4000 secondes montre que les repères XYZ et satellite sont confondus.
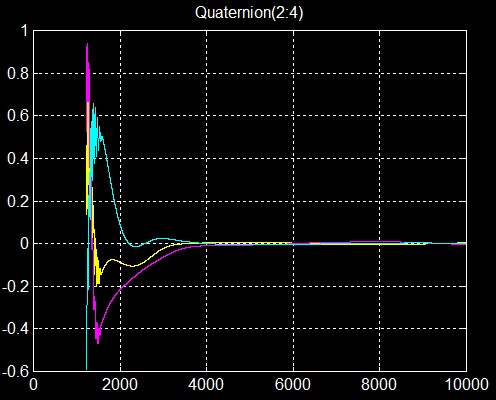

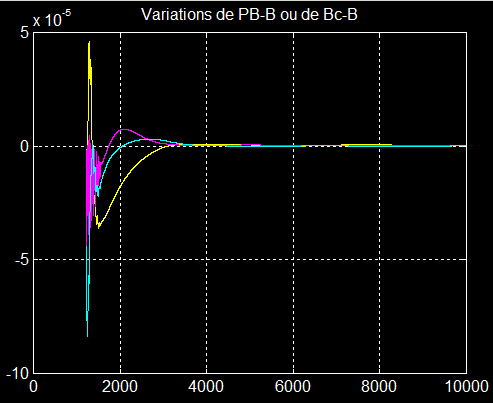
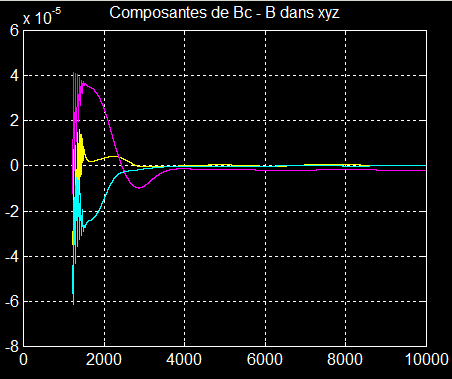
Confirmation remarquable de 4000 à10000 s (Bc=B)
On peut donc en déduire que xyz coïncide avec XYZ aux imperfections près de la simulation.
De plus la consigne Bc et B sont identiques en fin de simulation
3°) RESULTATS DE LA DEUXIEME SIMULATION ( Pointage nadir ):
ZENITH = -1
Repère de consigne XcYxZc ( Xc = - X, Zc = - Z )
Rotation < 0 de la roue autour de y
1° Vitesses angulaires : Le graphe des vitesses angulaires p q r dans les axes satellite, montre un amortissement parfait et des vitesses angulaires finales inférieures à 0.03 °/s, pour les 3 axes. Il est identique au cas précédent.
2°) Angles :
L'important est l'angle entre y et Y, que l'on devrait retrouver proche de 180°, ce qui est le but poursuivi.
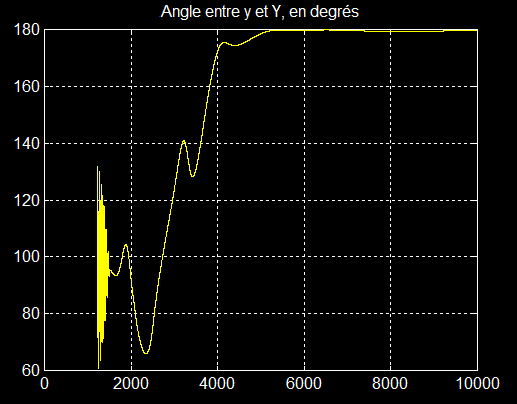
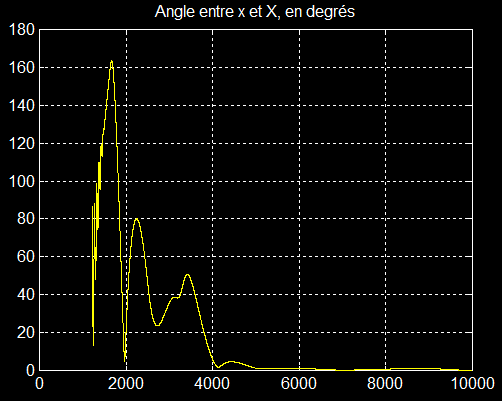
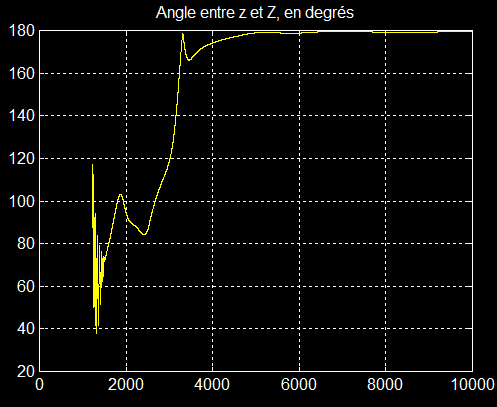
3°) Quaternion et attitude:
La comparaison des 2 graphes à partir de 4000 secondes montre que l'axe de rotation du quaternion est exactement l'axe X ( composante 1) et que l'on poasse de XYZ au satellite par une rotation d'angle 180° autour de X ( demi-tour )

I SIMULATIONS DE RETOURNEMENTS:
Pour mémoire nanolaur/Ret180_X initialisé par nanodat0
1°) Retournement autour de Z : nanolaur/Ret180_Z.m initialisé par retZ_dat.m, vitesse roue < 0
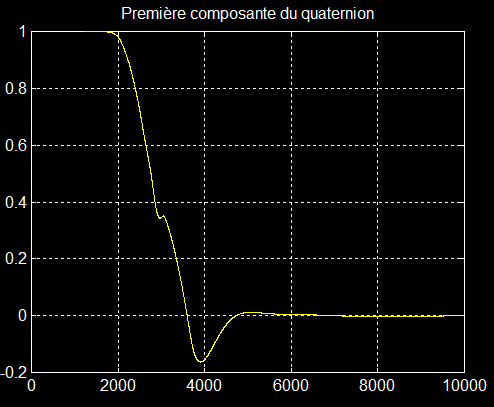
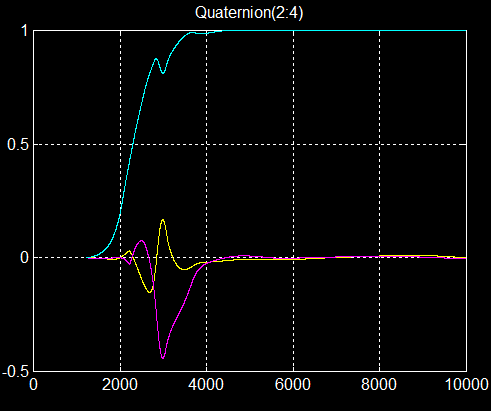
Le quaternion Q=[0 0 0 1] décrit complètement la rotation avec q0 = 0 = cos(a/2)=> a =180° et [0 0 1] = sin(a/2).Z = Z axe de la rotation

Confirmation de l'angle de lacet à 180°
2°) Retournement autour de Y : nanolaur/Ret180_Z.m initialisé par retZ_dat.m, vitesse roue > 0

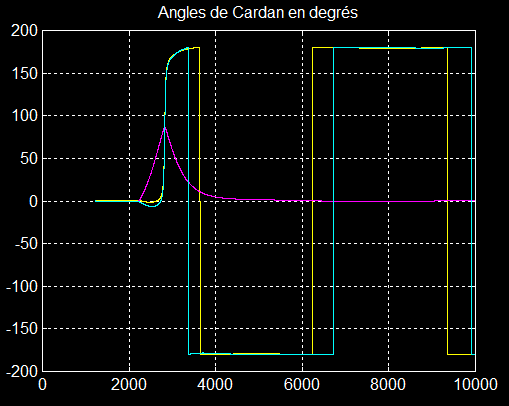
Le quaternion Q=[0 0 1 0] décrit complètement la rotation avec q0 = 0 = cos(a/2)=> a =180° et [0 1 0] = sin(a/2).Y = Y axe de la rotation

Confirmation des angles de lacet = 180° et roulis = 180°, tangage nul