|
COMPLEMENTS SUR LES SEQUENCES DE ROTATIONS ET LES QUATERNIONS D'ATTITUDE |
||
![]()
|
CONTENU : Rédigé
juin 2013 Mathématiques appliquées |
|
![]()
Dans
les cours sur les quaternions, cités dans l'en tête, je n'ai pas suffisamment développé l'aspect
calcul et géométrie des quaternions représentatifs des rotations.
Soit
Q un quaternion unitaire, les expressions suivantes
autorisent d'introduire, un angle q
( dont nous verrons l'interprétation ) et un vecteur unitaire u
( qui sera lui aussi caractéristique ):
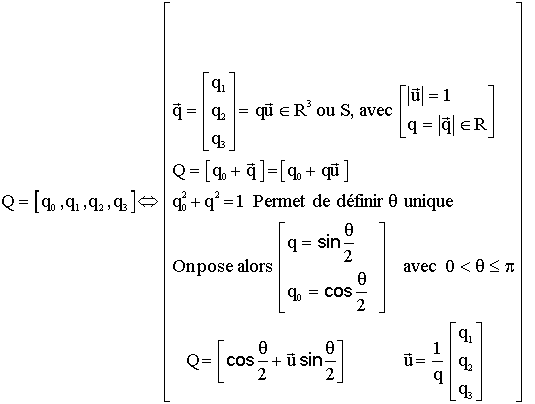
Cette
formulation du quaternion est fondamentale dans toutes les exploitations géométriques
que l'on peut faire des quaternions.

AVANT
GOÛT DU RESULTAT
:
Nous
montrerons plus loin que Q
représente complètement une rotation, par son
axe u et son
angle q
( j'ai bien dit q
et pas q
/2), on en attendait pas moins puisque avec 3 composantes ( le quaternion est
unitaire ) on peut bien paramétrer un vecteur unitaire ( 2 coordonnées indépendantes
) et un angle.
Rappelons le résultat du produit non commutatif de 2 quaternions exprimé sous la forme explicitée partie réelle et partie vectorielle. La présence du produit vectoriel justifie la non commutativité.
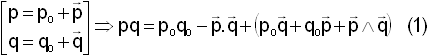
Le lecteur pourra aussi démontrer à titre d'exercice que :
![]()
2°)
Où on montre géométriquement que Q représente une rotation :
a)
Remarque
:
Si
on considère l'ensemble S des quaternions purs ( à partie réelle nulle ),
isomorphe à R3, muni de l'opération multiplication quaternionique,
on peut vérifier que cette opération n'est pas interne en général.

Ou encore en condensé :
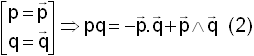
b)
Introduction d'une application
linéaire sur S ( ou R3 ) :
On pose comme définition de l'application LQ
![]()
Le lecteur vérifiera à titre d'exercices que l'application est linéaire
![]()
Qu'elle conserve les longueurs
![]()
-
Si on pose
-
![]()
-
Elle
laisse invariant le vecteur
![]()
Cette
propriété nous assure que l'opérateur conserve l'intégrité d'un corps
solide et donc que c'est une rotation, encore faut-il la caractériser.

Donnons, ce n'est pas inutile, une interprétation géométrique de la construction du transformé W d'un vecteur V .
Nous introduisons le vecteur unitaire U, la projection a de V sur U et posons un nouveau vecteur de m^me longueur que n, nommé m* et orthogonal à n.

Explicitons le calcul, surtout pour le transformé de m
![]()

Cette dernière relation montre clairement que le vecteur n se déduit de m par une rotation d'axe U, d'angle q.
3°) EXEMPLE D'APPLICATION EN GEOMETRIE :
On souhaite par exemple effectuer une rotation d'axe D ( pas nécessairement unitaire ) donné par ses composantes ( a, b, c ) et d'angle fixé q, sur un vecteur donné V de composantes (V1, V2, V3 ) et trouver rapidement le vecteur résultat. W
Il suffit d'associer à cette rotation un quaternion Q ( remarquez que l'axe de rotation est rendu unitaire )

II
SEQUENCES DE ROTATIONS ET QUATERNIONS:
C'est à la demande de certains étudiants que je rajoute cette rubrique sur les rotations et les suites de rotations, ce qu'on appelle " SEQUENCES DE ROTATIONS 3.
Leur usage est multiple soit :
- Mécanique du solide ( angles d'Euler, angles de Cardan, angles de roulis lacet tangage pour les aéronefs ou les satellites)
- Géométrie sur une sphère ( trigonométrie sphérique, polygones réguliers tracés sur une sphère ..)
- Trajectographie des satellites ( points survolés, paramètres orbitaux ...)
- Médecine ( étude des rotations résultant du fonctionnement des articulations ou mise au point de prothèses ...)
- Robotique en général .... etc...
1°) DEFINITION D'UNE SEQUENCE DE ROTATION ET NOTATIONS :
NB : pour éviter une prolifération de noms de vecteurs et de flèches, nous noterons toujours X Y Z ( en gras sans flèche ) les vecteurs de base des repères notés eux Ra pour l'ancien repère et Rn pour le nouveau. A la rigueur les vecteurs XYZ pourront être indexés, Xa Ya Za ou Xn Yn Zn
Notation d'une rotation : Une rotation d'angle a autour d'un axe Z par exemple sera notée ( a / Z ) et l'opération géométrique associée
Ra ___ ( a / Z ) ___ Rn
Est-il utile de rappeler les relations de transformation des axes , pour une rotation d'angle a autour de Z
| Ra ___ ( a / Z ) ___ Rn | Xn =
Xa cosa + Ya
sina
Yn = - Xa sina + Ya cosa Zn = Za |
Matrice de
passage associée au changement de base
|
NB : On pourrait aussi écrire avec la transposée ( ce que je ne recommande pas ) , mais qui représente mieux la rotation au sens géométrique et donc le deuxième tableau ci-dessus, avec la matrice R( a / Z ) que je nommerai opérateur de rotation.
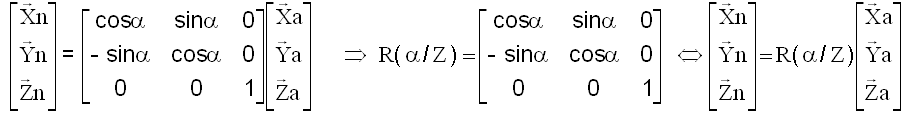
Faut-il rappeler que la matrice de passage est le tableau obtenu en écrivant les nouveaux axes sur les anciens comme ci-dessous,

mais que lors d'un changement d'axes, les composantes d'un vecteur V ( v1 v2 v3 ) dans l'ancienne base deviennent V ( V1 V2 V3 ) dans la nouvelle base comme suit, dans un sens qu'on a tendance à oublier. :
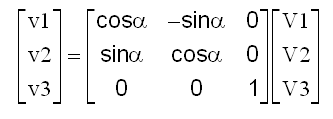
Rappelons aussi que pour les matrices de passage ( dites orthogonales ) l'inverse s'obtient par la transposée.
Séquence de rotation : c'est une suite de rotation définies chacune par un axe et un angle, avec comme seule contrainte que l'axe appartienne à un repère orthonormé.
Ainsi nous noterons
Ra ___ ( a / Y ) ___ ( b / Z ) ___ ( g / X )..___ ..( s / Y ) ___ Rn
une suite de rotations consécutives menant du référentiel Ra au référentiel Rn.
On distingue alors 2 types de séquence de rotation :
1 - Séquence ouverte, où le dernier repère est différent de celui de départ
2 - Séquence fermée, où le dernier repère est celui de départ, comme figuré ci-dessous
Ra ___ ( a / Y ) ___ ( b / Z ) ___ ( g / X )..___ ..( s / Y ) ___ Ra
ou encore
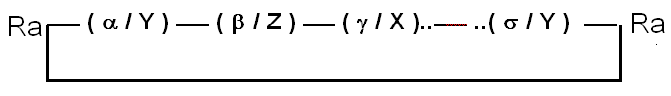
2°) INTERET DES NOTATIONS SIMPLIFIEES POUR LES AXES : :
Le fait de toujours noter x y z ou X Y Z ou encore 1 2 3 ,les axes des repères successifs, permet de "mécaniser" les écritures soit des matrices soit des quaternions, ce qui est un gros avantage en cas de programmation informatique.
Ce que nous résumons, en donnant les matrices de passage notées P( angle / axe), ( au sens classique ), les matrices opérateurs de rotation notées R( angle / axe) et les quaternions associés notés q ( angle / axe). :
| Rotations | Ra ---- ( a / Z ) ---- Rn | Ra ---- ( b / X ) ---- Rn | Ra ---- ( g / Z ) ---- Rn |
| Matrice passage | 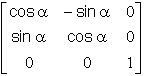 |
 |
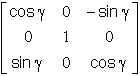 |
| Matrice opérateur de rotation | 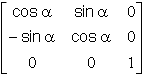 |
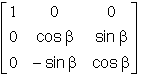 |
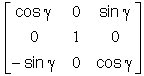 |
| Quaternions associés |
3°) EXEMPLE INCONTOURNABLE, LES ANGLES D'EULER :
Pour la définition, certainement connue du lecteur, revoir éventuellement l'article dédié..
a) Avec les matrices :
La suite des rotations ( passage du repère fixe au repère lié au solide, avec précession y, nutation q , rotation propre j ) est :
( y /z ) ---- ( q , x ) ---- ( j /z ), ainsi la matrice de passage se calcule par P (y, q, j) = P( y ) P( q ) P( j ) , ce qui donne :

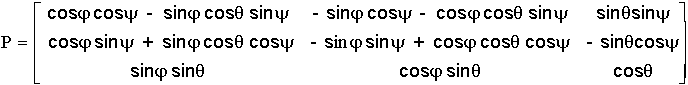
Le quaternion résultant de la séquence d'Euler se calcule par :

Tous calculs effectués ( en application des règles de calcul ij=-ji=k, jk=-kj=i, ki=-ik=j, i²=j²=k²=ijk=-1 ) il vient ( c'est assez simple )

et surtout une belle symétrie d'écriture.
b) Paramètres orbitaux analogues des angles d'Euler :
Partant du repère fixe géocentrique équatorial, pour arriver au repère orbital R T N, le lecteur se convaincra que la séquence est identique à celle d'Euler
Ra --- (W/z) ---- (i/x) ---- ((w+q)/z --- Rn
Le quaternion est simple à adapter, avec l'analogie W <-> Y i <-> q (w+q) <-> j
5°) UTILISATION DES SEQUENCES DE ROTATION : :
1 - Intérêt d'une séquence fermée : Une séquence fermée peut être décomposée en une suite de 2 séquences ( séquence 1, Matrice M, quaternion m, , séquence 2, matrice N, quaternion n ) comme c-dessous:
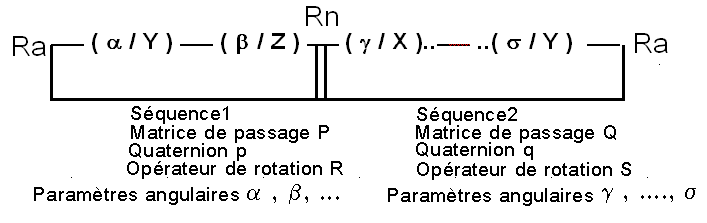
Alors les relations entre matrice et opérateurs sont simples :
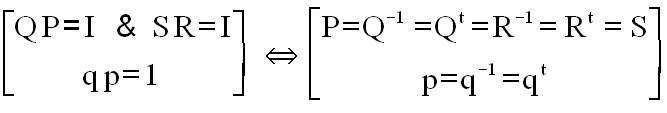
mais surtout, en pratique il faut les exploiter pour obtenir des relations entre les paramètres de configuration a, b, ... et g, s.
2 - Utilisation de 2 séquences identiques avec des paramètres différents :
Soit on écrit l'égalité des matrices ou des quaternions de chaque séquence et on en déduit des relations entre les paramètres des 2 séquences.
Soit on se ramène à une séquence fermée, en gardant la première séquence suivie de l'inverse de la deuxième. On exploite alors les conséquences d'une séquence fermée comme en 3°)
III
SEQUENCES DE ROTATIONS PARTICULIERES :

ABC est un triangle sphérique sur une sphère de centre O. On introduit un repère X Y Z avec Z porté par OA et le plan YZ contenant l'arc de cercle AC.
Tout le monde connaît la définition des angles au sommet A, B, C avec un chapeau et les angles au centre a b c en minuscules. Pour éclairer la sé"quence de rotations, je donne les divers axes sur la figure. Nous illustrons une séquence fermée.

Nous nous ramenons donc aux notations simplifiées :

La séquence étant fermée, on peut la couper en 2 parties, pour obtenir des relations entre des paramètres différents,
Par exemple:

donnera des relations entre b, c, C et B, c, A, comme ci-dessous, obtenue avec :
1 - Avec les matrices opérateurs de rotation
On écrit P Q= I entraînant P = Q-1 = Q* ( transposée de Q ) soit


ce qui donne avec P = Q*
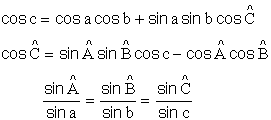
avec en déduction des formules classiques généralisables par permutation circulaire des lettres A B C et a b c :

Et finalement
Formules auxquelles on peut rajouter ( le lecteur fera les calculs ), les relations dites des cotangentes

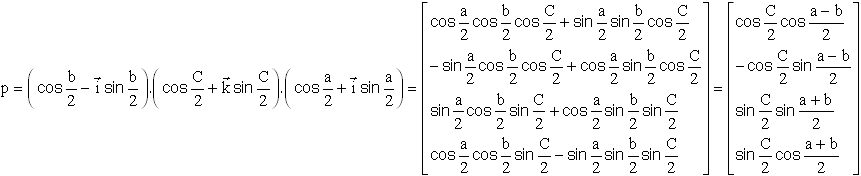
Un calcul analogue avec le quaternion q donne :

La séquence fermée entraîne p = q*, soit une série de relations plus ou moins intéressantes reliant les demi angles, soit

Bien évidemment, par permutation circulaire ( correspondant aux séquences commençant par les autres points ) on trouve encore 8 relations.
Essayons de retrouver la relation des sinus ( En utilisant les propriétés des proportions), laissant le soin au lecteur de retrouver les autres relations.
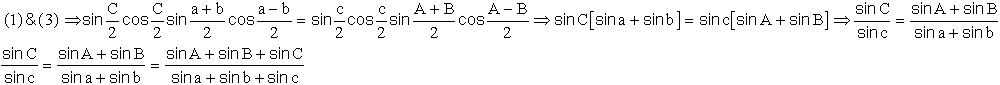
Il vient donc la fameuse relation des sinus
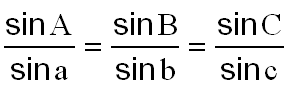
2°) PARAMETRES ORBITAUX ET EPHEMERIDES : Voir les calculs spéciaux dédiés
3°) Calculs relatifs aux polygones réguliers inscrits dans une sphère. Voir exercice et solution
Guiziou Robert juin 2013
Bibliographie :
Très intéressant pour l'astrométrie et les problèmes d'heures
Très complet et rigoureux ( notamment triangles sphériques )
Remarquable cours de mathématiques appliquées sur les angles d'Euler, les vitesses angulaires associées, les singularités de la représentation devrait intéresser le mécanicien des mouvements de solides
Résolution informatique des singularités de la représentation d'Euler