POLYGONES INSCRITS SUR UNE SPHERE Juin 2013

 | Voir le cours sur les quaternions | Voir la solution |

Remarque initiale: dans cet exercice, il sera question de polygones réguliers inscrits sur une sphère, c'est à dire que tous les sommets du polygone appartiennent à une sphère de rayon R

Notations :

Dans tous les cas nous noterons en majuscule A, B, C les sommets, a l'angle au sommet ( entre les tangentes X et U aux grands cercles ), a l'angle au centre qui va donc définir la longueur du coté du polygone régulier.

Pour fixer les idées, un repère X Y Z est défini comme repère de départ d'une séquence de rotations.

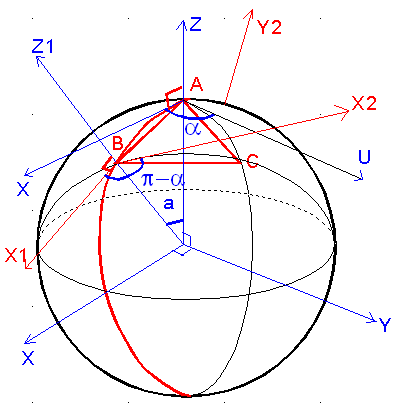
I CAS DU TRIANGLE EQUILATERAL:

1°) Montrer que la séquence élémentaire S1 définie par:

- La rotation d'axe Y, d'angle a suivie de

- La rotation d'axe Z1 d'angle p-a,

transforme le grand cercle de AB en celui de BC. En déduire les quaternions associés à chaque rotation, puis le quaternion Q (a, a )associé à la séquence, noté 

2°) En déduire que Q³ = I puis

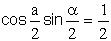
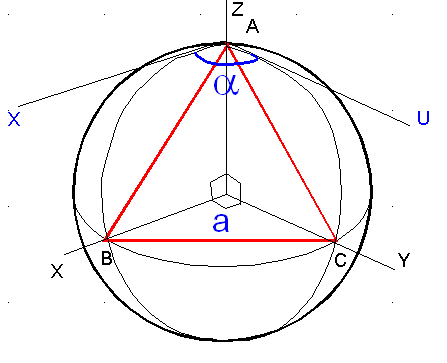
3°) Vérifier sur le cas particulier ci-dessous que tout va bien.

4°) Calculer les éléments caractéristiques, pour inscrire un triangle équilatéral de coté 1 m dans une sphère de 1 m de rayon.

II GENERALISER AU CAS D'UN CARRE INSCRIT

Avec les mêmes notations, déduire la relation caractéristique :

SOLUTION SUCCINCTE

1°) Calcul de Q

Il est clair que la rotation d'angle a, transforme A en B, l'axe X devient X1 les 2 restant tangent au grand cercle passant par A et B. La deuxième rotation transforme le grand cercle de AB en celui de BC

:Nous gardons les notations présentées dans ce site ( les voir ), donc S1 est caractérisée par :

X Y Z --- ( a/Y) ---X1 Y Z1 ----[ (p-a)/Z1 ] ----  X2 Y2 Z1

:Ou encore en notations classiques et les quaternions

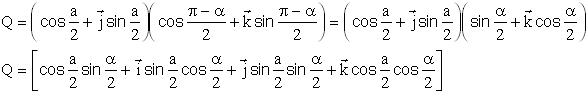
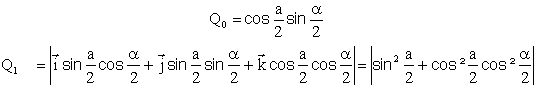
2°)On calcule Q³

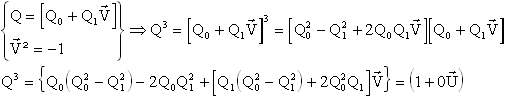
Il faut traduire que le résultat est un quaternion unité

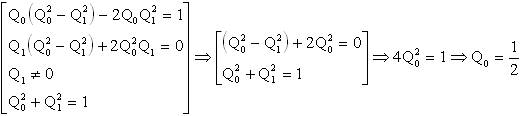
Et donc

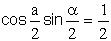
3°) Vérification sur le cas particulier:

De toute évidence, on a:

relation vérifiée.

4°) Calcul des éléments caractéristiques, pour inscrire un triangle équilatéral de coté 1 m dans une sphère de 1 m de rayon.

Le coté du triangle vaut L = 2 R sin(a/2) donc sin(a/2) = 1/2 soit a = 60°

L'angle a vaut donc

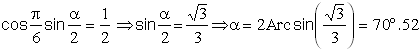
II GENERALISATION AU CAS D'UN CARRE INSCRIT

Le lecteur, initié à la méthode fera l'effort de résoudre lui-même la question, pour trouver :

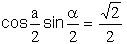
Guiziou Robert juin 2013