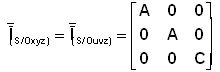ANGLES D'EULER ET ROTATION

CONTENU:  Mis à jour janvier 2005, revu sept 2011, avril 2013 

 

I DEFINITION DES ANGLES

II ROTATIONS ELEMENTAIRES

III MATRICE DE PASSAGE

IV ROTATION INSTANTANEE

V MOUVEMENT DE LAGRANGE ET POISSON

 

Ce paragraphe est consacré au repérage d'un solide ( ou d'un repère R mobile xyz ) en mouvement par rapport à un référentiel Ra considéré comme fixe, dont les axes sont notés X Y Z. Souvent ce dernier est galiléen, mais ce n'est pas une nécessité.

Nous savons par les mathématiques que trois rotations sont nécessaires pour passer de Ra à R. Le choix des angles n'est naturellement pas unique et dépend de la nature du problème à étudier. Bien que les angles d'Euler ne soient pas les plus commodes, ils font partie d'un repérage classique en mécanique du solide. Ils sont tout de même couramment utilisés en mécanique classiqe, goniométrie et repérages spatiaux…

NB : vous trouverez ailleurs sur ce site, une présentation des angles de roulis - lacet - tangage. En anglais vous rencontrerez en aéronautique  q Pitch ( tangage ) - F Roll ( Roulis ) -  Y Yaw ( Lacet ), mais je ne préconise pas ce rapprochement, sauf cas particulier.

AVERTISSEMENT :  Les calculs qui vont suivre, font partie de la branche des mathématiques qui traite du calcul matriciel, des transformations des composantes, des matrices de passage, des matrices unitaires de leurs inverses ou transposées …

Ne voulant pas réécrire toutes les mathématiques ( ce qui serait prétentieux ) je vous oriente plutôt vers quelques sites qui traitent de la question générale des  SEQUENCES DE ROTATIONS , sites malheureusement en anglais ( en 2013 )

Site 1 : Stellar software

Site 2 : Document Word en anglais excellent niveau, sérieux et général

Site 3 : Document pdf de très grande qualité, faisant les rappels nécessaires sur les rotations et le joint avec les quaternions, notion qui est présente sur mon site

Site 4 : Traitant du calcul inverse des angles d'Euler, connaissant la matrice de passage, avec étude précise des cas limites. Rubrique très utile pour ceux qui se lancerait dans une programmation informatique.

I DEFINITION GEOMETRIQUE ET INCONVENIENTS :

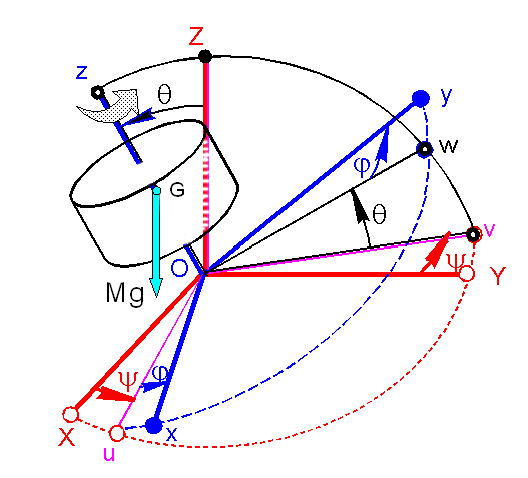
Le croquis ci-dessous devrait éclairer l'exposé succinct de ces angles.

BUT: "Passer" de Ra à R, par 3 rotations, à l'aide de 2 repères intermédiaires.

MOYEN : Le plan Oxy coupe en général le plan OXY suivant une droite, sur laquelle on choisit arbitrairement un demi axe unitaire noté Ou. Ceci permet de définir un premier angle y:

 Y angle de PRECESSION mesuré positivement autour de OZ.

INCONVENIENT : Il existe une configuration ( celle ou la nutation q vaut 0 ou 180 ° )où les 2 plans sont confondus, rendant difficile le suivi de y, sauf à le suivre par continuité. Ce problème a une incidence certaine dans les résolutions informatisées.

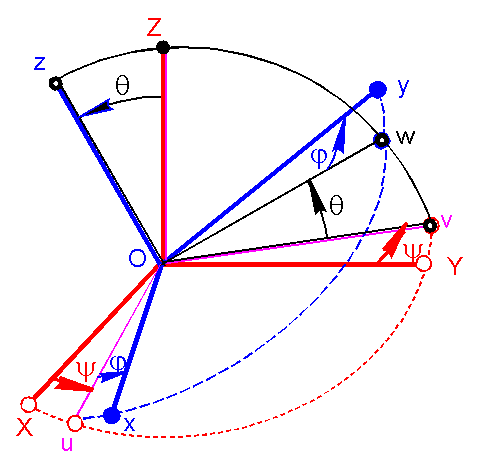
Les 2 autres angles ne présentent alors pas de difficulté:

 q angle de NUTATION est l'angle orienté des unitaires X et u, mesuré >0 autour de Ou.

 j angle de ROTATION PROPRE est l'angle orienté des unitaires u et x, mesuré >0 autour de Oz.

II ROTATIONS ELEMENTAIRES:

La chaîne des rotations logiques est la suivante :

1 - Ra = XYZ est transformé en uvZ par la rotation d'angle y autour de Z.

2 - uvZ est transformé en uwz par la rotation d'angle q autour de u.

3 - uwz est transformé en R = xyz par la rotation d'angle j autour de z.

III MATRICE DE PASSAGE:

Rappel : La matrice de passage P du repère x y x à X Y Z est construite avec les colonnes composantes des vecteurs X Y Z sur x y z  respectivement.

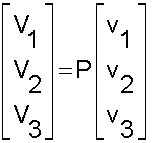
Si vous l'avez oublié un vecteur V de composante V1 V2 V3 dans le repère fixe et v1 v2 v3 dans le repère mobile, vérifie :

Le lecteur peu à l'aise dans les changements d'axe pourra établir la matrice de passage P(Ra-->R)=(Pij) que voici:

Colonne 1:

P11 = cosj cosy - sinj cosq siny

P21 = cosj siny + sinj cosq cosy

P31 = sinj sinq

Colonne 2:

P12 = -sinj cosy - cosj cosq siny

P22 = -sinj siny + cosj cosq cosy

P32 = cosj sinq

Colonne 3:

P13 = sinq siny

P23 = -sinq cosy

P33 = cosq

Soit la matrice de passage ( Fixe vers mobile ) ou Matrice des cosinus directeurs, ou encore DCM en anglais ( Direction Cosine Matrix )

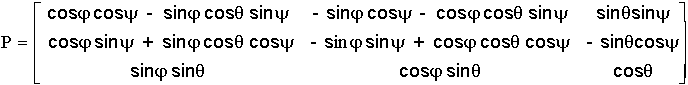
REMARQUE :

Vous rencontrerez plus loin la théorie des quaternions qui est, de très loin, la meilleure manière d'appréhender les rotations d'un solide, surtout quand elles peuvent être quelconques ( Satellites en perte de contrôle ou en mode survie, avion en voltige etc...). Attention les quaternions sont d'un abord difficile.

Bref, la fin d'un calcul avec les quaternions donne la matrice instantanée P ( exprimée à l'aide des composantes du quaternion d'attitude , disons que l'on connaît les valeurs des Pij ), avec laquelle il faut reconstituer l'attitude, c'est à dire les angles d'évolution du solide en mouvement. Pour nous ici, il faut retrouver les angles d'Euler. Il s'agit donc de résoudre le système d'équations qui suit, avec comme inconnues y q f .

[1] P11 = cosj cosy - sinj cosq siny

[2] P21 = cosj siny + sinj cosq cosy

[3] P31 = sinj sinq

[4] P12 = -sinj cosy - cosj cosq siny

[5] P22 = -sinj siny + cosj cosq cosy

[6] P32 = cosj sinq

[7] P13 = sinq siny

[8] P23 = -sinq cosy

[9] P33 = cosq

Si l'on considère qu'un angle est parfaitement défini par son sinus et son cosinus, on peut considérer qu'il y a 6 inconnues, siny, cosy, sinj, cosj, sinq, cosq, et donc que 6 équations sont nécessaires sur les 9.

Comme dans chaque paquet de 3 équations, les 2 premières entraînent la troisième, il y a 3 équations surabondantes.

IV ROTATION INSTANTANEE:

Le lecteur validera ses compétences en mécanique classique pour établir les composantes du vecteur rotation instantanée de R par rapport à Ra :

EN AXES FIXES DE Ra:

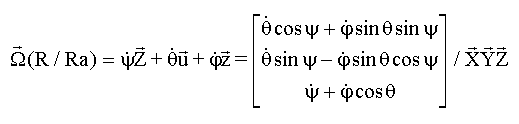
EN AXES MOBILES DE R :

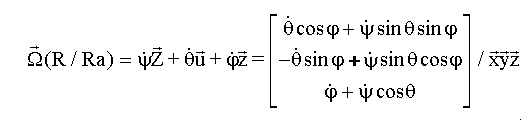
V EXEMPLE CONCRET POUR LES AMATEURS DE MATLAB: Le mouvement dit de 'Lagrange et Poisson'

En tant qu'enseignant, je trouve, bien que ce soit un cas d'école, cet exemple excellent pour illustrer de nombreuses techniques :

1.     Le théorème du moment cinétique en axes mobiles

2.     L'usage de l'informatique et surtout de Matlab qui permet de parfaitement simuler à peu de frais le mouvement

3.     La mise en œuvre des quaternions

4.     L'exploitation des quaternions pour reconstituer l'attitude

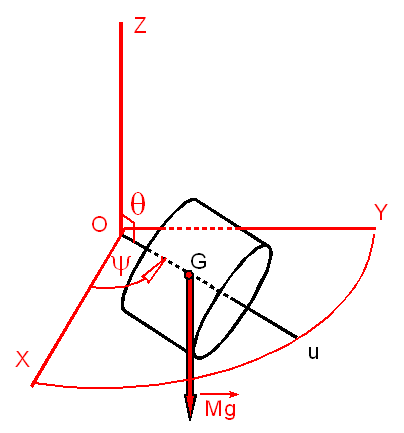
1°) DEFINITION :

Le mouvement de Lagrange et Poisson est celui d'un solide (S) , mobile autour d'un point fixe O , origine d'un repère inertiel OXYZ ( Z vertical ascendant ), avec les qualités suivantes :

  1. Le solide (S) possède un repère principal Oxyz dans lequel la matrice d'inertie est de révolution autour de l'axe oz.
  2. Le centre d'inertie G appartient à l'axe oz
  3. Les articulations classiques des armatures de Cardan sont sans frottement et de masse nulle ( cas d'école), mécaniquement, elles sont équivalentes à une articulation sphérique parfaite qui maintient O fixe.
  4. Le mouvement a lieu sous le seul effet de la pesanteur orientée en sens contraire de Z.
  5. APPLICATION PRATIQUE: Le mouvement illustre la précession et la nutation d'un "gyro" de verticale balourdé.

  1. Notations : On appelle :

Pour la pesanteur

Pour les inerties

 

W

La rotation axiale initiale autour de z

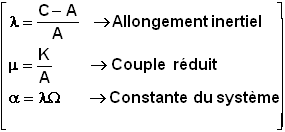
p, q, r

les composantes de la rotation absolue de S exprimée sur x y z

Constantes pour la suite des calculs

L'articulation en O qui maintient O fixe est sphérique parfaite, Le seul couple actif sur le solide S est celui Co de la pesanteur, porté par l'axe Ou.

2°) EQUATIONS DU MOUVEMENT

  1. Résolution par les quaternions :

Le quaternion Q = ( q0 q1 q2 q3 ) qui sera introduit, est associé à la rotation qui transforme le repère absolu fixe XYZ en celui, mobile xyz lié au solide S. L'usage des quaternions nous libère, à priori de toute définition plus ou moins bien définie des angles. Si des angles deviennent nécessaires, alors dans cet exercice, ce seront typiquement ceux d'Euler y, q, j.

Le théorème du moment cinétique, appliqué au point fixe O, en projection sur les axes satellite, conduit aux équations classiques :

Le couple est alors exprimé en termes de quaternions ( voir le cours ), la matrice de passage est P=(Pij)

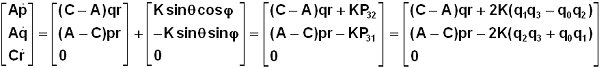
La résolution numérique consiste à former un système différentiel du premier ordre, avec une variable vecteur colonne à 7 composantes ( 3 pour la rotation ( p q r ) et 4 pour le quaternion Q = ( q0 q1 q2 q3 ) . Naturellement vous constatez que r(t) est constant et reste égale à W. La rotation axiale se conserve.

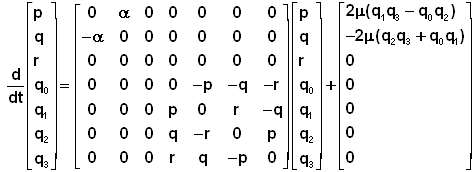
Système classique de la forme :

Pour l'initialisation, il faut voir le cours sur les quaternions.

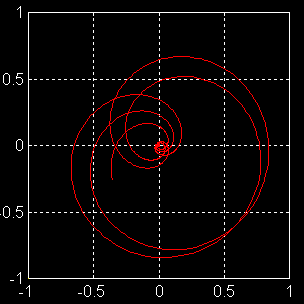
b) Résultats : les graphiques qui suivent illustrent une simulation Matlab.

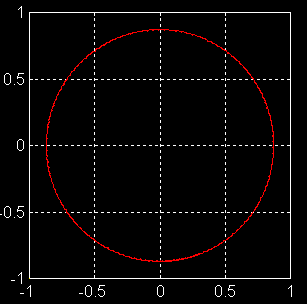
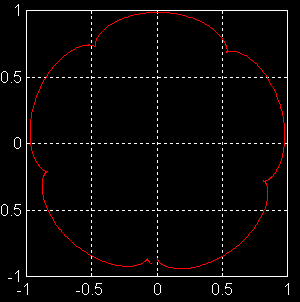
Figure 1 : Cas classique avec un lancement du "gyro" très particulier :

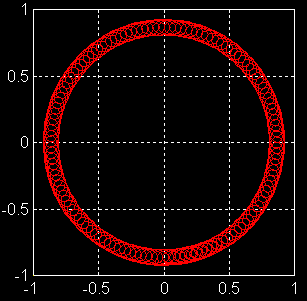
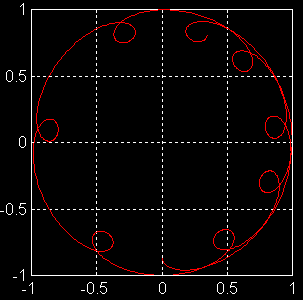
Figure 2 : Seul changement par rapport à fig1, on donne un peu de vitesse de nutation et donc on assiste à une courbe en festons serrés entre 2 cercles, prouvant que q oscille entre 2 valeurs.

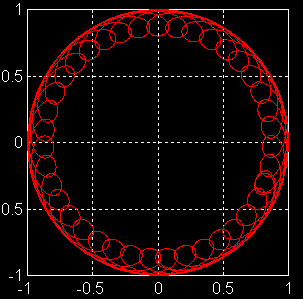
Figure 3 : Par rapport à fig2, on a diminué la rotation propre dans un rapport de 5.

La trajectoire présente alors des points de rebroussement.

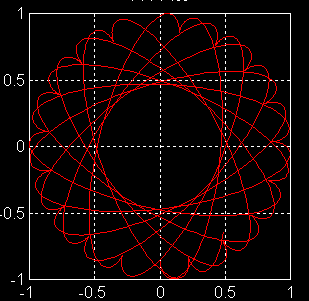
Figure 4 : Diminution de la vitesse angulaire et apparition de festons plus "larges" qu'en figure 2

Figure 5 : Comme en figure 3 mais sur un temps plus long.

Figure 6 : Augmentation de la masse et diminution de la rotation propre è Plus grande amplitude des variations de la nutation q.

Figure 7 : L'axe est supposé quasiment vertical au départ q voisin de è On assiste alors à une descente de l'axe et une remontée vers la quasi verticale, ce qui donne en projection sur le plan, une sorte de "cardïoide".

 

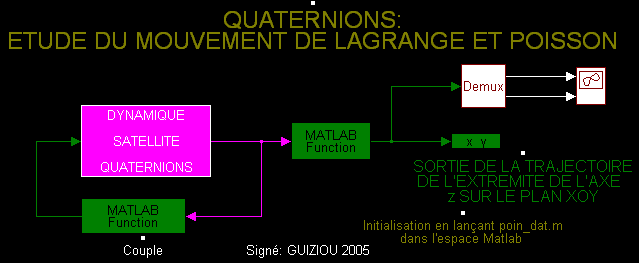
Schéma du diagramme fonctionnel sous Matlab/Simulink

 

Ensemble des fichiers récupérables Lagrange.zip

 

 2°) AUTRES EQUATIONS DU MOUVEMENT :

a) MISE EN EQUATIONS CLASSIQUE :

Classiquement, en mécanique générale, avec un paramétrage par les angles classiques d'EULER, on écrit d'autres équations, par le théorème du moment cinétique, appliqué à S, en O fixe, en projection sur les axes uvz, axes qui restent principaux pour S et privilégiés pour le calcul du couple du à la pesanteur.

Le lecteur passionné de mécanique confirmera les calculs qui donnent le système :

 

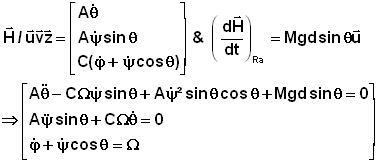
On retrouve la conservation de la rotation axiale, mais les 2 premières équations ne permettent pas une résolution "à la main". Cependant, un cas particulier intéressant et étonnant est celui de l'existence d'un mouvement où q=90° reste constant, à la seule condition que la précession prenne une valeur bien précise.

b) MISE EN EVIDENCE D'UN COMPORTEMENT GYROSCOPIQUE:

Recherchons la possibilité d'un mouvement stationnaire où q reste constant. De toute évidence la vitesse de précession vérifie l'équation :

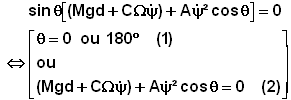
L'équation (1) montre la fixité de l'axe en position verticale, ce qui est normal puisque la pesanteur devient inactive.

L'équation (2) donne une autre solution avec la vitesse de précession dy/dt en fonction de q et W.

Le cas intéressant est celui où le solide S est un gyroscope animé d'une grande vitesse angulaire W,.On peut alors montrer que :

Ce cas est illustré par la figure (1) avec les conditions initiales bien choisies. C'est, ce que l'on appelle le PARADOXE GYROSCOPIQUE: A savoir que le solide S est complètement en porte à faux où le poids agit avec un couple maximum et cependant l'axe Oz du solide reste dans le plan horizontal, "sans tomber".

APPLICATION PRATIQUE :

La conséquence de ce résultat, est que pour un "gyro" dit de pointage ( devant mémoriser une direction absolue ), tout décentrage de G par raport au point de suspension O, crée une précession et donc une dérive de l'axe "gyro". C'est un point critique des techniques inertielles. On y remédie en pratique en augmentant au maximum la vitesse angulaire axiale W , ce qui fait diminuer la dérive. 

Guiziou Robert , avril 2013