Cette page est destinée à bien préciser l'utilisation des quaternions lors d'un produit correspondant à des changements de repère et surtout du calcul des rotations  du paramétrage d'un corps mobile.

En effet, si l'on fait uniquement de la géométrie, généralement les rotations successives sont faites autour d'axes repérés dans le repère de travail, dit "FIXE". Le produit des quaternions s'opèrent alors comme une composition d'applications successives.  

I CALCULS EN REPERE FIXE:

Une rotation d'angle a₁ autour d'un axe D₁, suivie d'une rotation d'axe a₂ autour de D₂ etc....est globalement représentée par un quaternion produit des 2 rotations élémentaires,  exprimées dans le repère fixe.

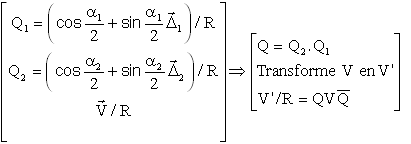
Exemple avec les 2 premiers angles d'Euler :

Sans revenir à la définition de ces angles, donnons la figure et rappelons les 2 premiers angles

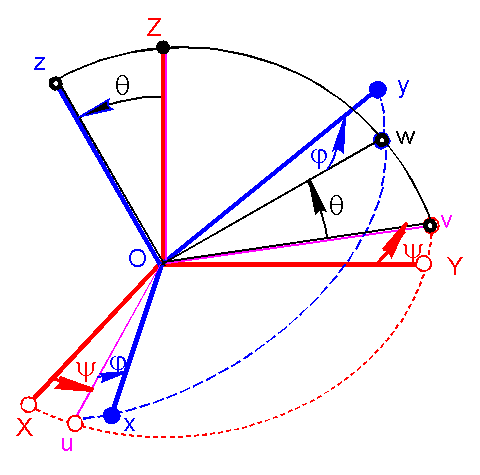
 y angle de PRECESSION est l'angle orienté des unitaires X et u, mesuré >0 autour de OZ, transforme R₁ = XYZ en R₂ = uvZ

 q angle de NUTATION est l'angle orienté des unitaires Z et z, mesuré >0 autour de Ou. transforme ensuite R₂ = uvZ en R₃ =  uWz

a) Quaternions: Il est nécessaire d'exprimer Q₂ dans la base initiale

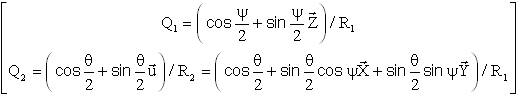
b) Produit classique avec résultat dans R₁

_{Le lecteur établira}

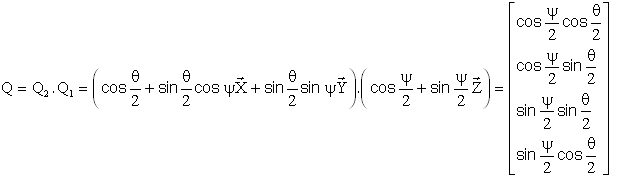
on notera l'élégance du résultat.

II CALCULS UTILISANT LES REPERES INTERMEDIAIRES:

Couramment en mécanique avec des solides articulés les uns par rapport aux autres, le paramétrage utilise des angles mesurés dans des repères tournants avec des axes de rotation eux aussi associés à des solides mobiles.

Exemples:

1 - Solide mobile autour d'un point fixe ( mouvement de Poinsot, gyroscopes )

Repérage par les angles d'Euler

Repérage par les angles de Cardan ( cas de petits angles )

2 - Avion dont l'attitude est associée aux angles de Roulis - Lacet - Tangage

3 - Satellite avec repérage par rapport au repère orbital, certes mobile, mais souvent considéré comme le repère R₁ de référence de l'attitude.

4 - Prothèses osseuses plus ou moins complexes

5 - Robotique, notamment avec des bras articulés et des pinces ...

Dans tous les cas, un repère fixe de départ est nécessaire on le notera R₁ 

Point commun de tous ces problèmes:

1 -Chaque articulation d'un solide i par raport au solide i-1, se fait autour d'un axe lié au solide i-1. Ces rotations sont donc particulièrement simples à modéliser avec un quaternion.

2 - De plus les calculs sur ordinateur demandent moins de mémoire avec les quaternions qu'avec les matrices  ou autres calculs vectoriels.

3 - Seule difficulté ( nous verrons qu'en fait ce n'est pas le cas ) les quaternions ne sont simples que dans les repères intermédiaires, alors que les résultats doivent se terminer en repère  de référence R₁

_{EXPRESSION DU PRODUIT DES QUATERNIONS :}

Soient donc donnés:

     2 repères R₁ ( de base fixe i j k ) appelé "fixe", et R₂ ( de base mobile e₁ e₂ e₃ ) le deuxième qualifié de mobile

    Q₁ le quaternion associé à la  rotation transformant i j k en  e₁ e₂ e₃ 

    Q₂ = (a₀ a₁ a₂ a₃ ) un quaternion exprimé dans la base de R₂ 

a) Traduction de Q₂ en base fixe :

Le quaternion Q2 doit être ramené dans la base fixe. Ceci peut être réalisé par un calcul matriciel de changement de base, mais, pour nous, il vaut mieux utiliser la rotation de quaternion Q1.

Comme a₀ est la composante neutre 

Ainsi:

Q2 opérant dans R2	Q2 traduit dans R1 en explicitant les vecteurs de base de R2

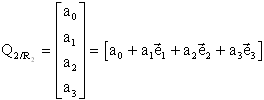
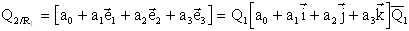
b) Expression du produit des rotations :

Comme nous travaillons dans R₁, nous effectuons le produit comme celui de la composition des applications successives, soit

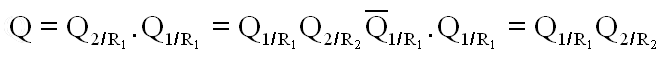
On constate alors que le produit doit s'opérer dans l'ordre des opérateurs.

Cette relation se généralise à n rotations successives:

b) CONCLUSION TRES IMPORTANTE :

Un produit de quaternions traduisant la composition de rotations, avec les quaternions Q_k/Rk ( k=1,....,n ) exprimés dans R_k doit être effectué dans l'ordre des rotations

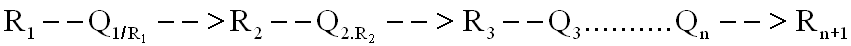
R₁ ----- Q  ---->  R_n+1

Q = Q1_/R1.Q2_{/R2 --------}  Qn_/Rn

Illustration : ( avec l'exemple plus haut, des 2 premiers angles d'Euler )

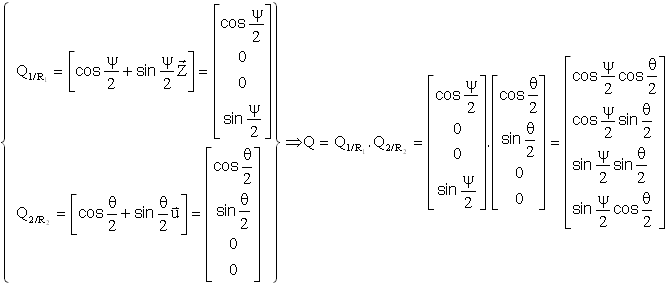
Nous retrouvons bien évidemment le même résultat;

Où l'on pousse le raffinement du calcul par une notation simple:

Généralement, dans les séquences de rotation, on passe d'un repère au suivant par une rotation autour d'un des axes du repère. L'astuce consiste à suivre leur évolution, soit par les notations de base i, j, k ou x, y, z, ou X, Y, Z. Ma préférence va à i, j, k, pour lesquelles les règles de calcul ont été présentées.

On écrit alors : utilisant i²=j2=k²=-1, i.j=-j.i=k,  j.k=-k,j=i, .k.i=-i.k=j , au lecteur de calculer?

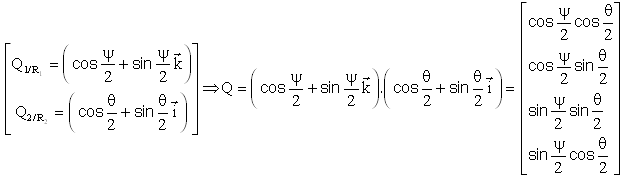
III CALCULS UTILISANT LES REPERES INTERMEDIAIRES:

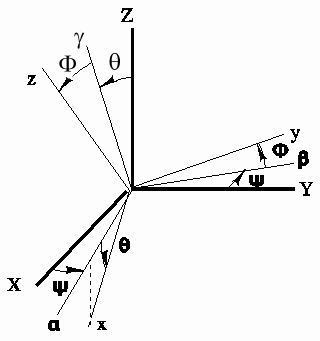
Vous retrouverez ces rubriques ailleurs dans le site.  XYZ est le repère orbital classique

1°) Angles de Cardan :

Les repères sont définis comme suit, après avoir indiqué que l'axe a est la projection sur le plan horizontal X, Y de l'axe x. La succession de repères est :

XYZ --- Y --> abZ -- q ---> xbg --- F --> xyz

Nous avons ainsi défini les angles conventionnels, également appelés ANGLES DE CARDAN :

• Lacet y mesuré autour de Z
• Tangage q mesuré autour de b ( voisin de Y lorsque les angles sont petits)
• Roulis f mesuré autour de x ( voisin de X lorsque les angles sont petits)

Mettons en oeuvre le calcul raffiné:

2°) Angles d'Euler : 

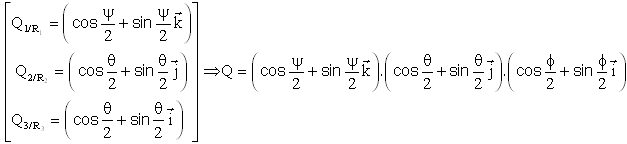
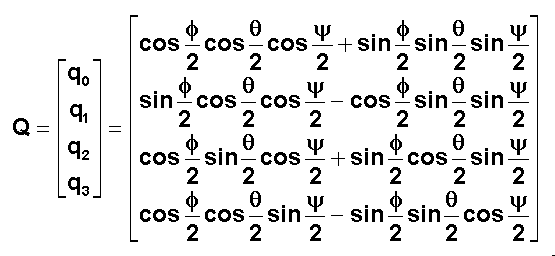
Revoir la figure plus haut

Là aussi vous retrouverez certains des calculs ailleurs dans le site. 

Le quaternion résultant de la séquence d'Euler se calcule ( toujours en utilisant l'écriture des quaternions élémentaires en repère relatif ) par :

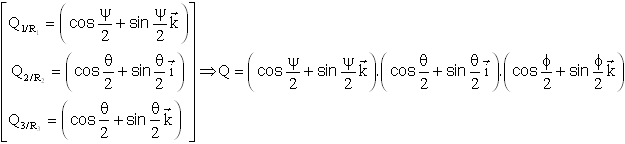
Tous calculs effectués ( en application des règles de calcul ij=-ji=k, jk=-kj=i, ki=-ik=j, i²=j²=k²=ijk=-1 )  il vient ( c'est assez simple )

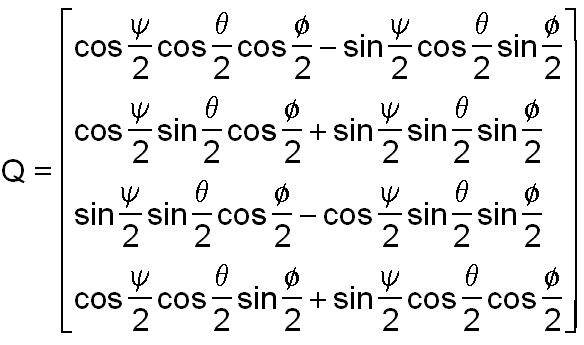
Guiziou Robert août 2013

Bibliographie :

Excellent cours de Michel Llibre, qui m'a permis de vérifier mes calculs

Cours très théorique sur lesquaternions pour matheux uniquement