PROGRESSION DES SIMULATIONS
VERS LE CONTRÔLE SATELLITE FINAL
![]()
![]()
Outils Matlab - Simulink
Cette page donne l'historique des simulations successives mises au point, pour arriver à la synthèse des opérations à réaliser:
- 1 Après la mise en orbite, le satellite est dans la configuration la plus complexe car les vitesses angulaires sont importantes, les angles évoluent très vite et donc l'attitude est totalement aléatoire. C'est la première phase dite de " détumbling " ou de réduction des vitesses angulaires.
- 2 A la fin de cette phase la configuration angulaire de vol n'est pas acquise et nécessite une régulation particulière dite d'acquisition grossière. Elle nous conduit à une attitude de travail avec des vitesses angulaires faibles.
- 3 Le satellite est alors libre, simplement sous surveillance et les perturbations vont l'écarter des conditions de travail, jusqu'à ce que les capteurs commandent un changement de régime.
- 4 C'est la phase de régulation du pointage fin qui se termine à nouveau par un passage au régime libre etc.. etc..
- 5 A la suite de nombreuses régulations fines alternant avec des régimes libres, la roue ( si elle est utilisée pour son couple réactif ) finit par atteindre des vitesses élevées et demande à être " désaturée " c'est la dernière opération du cycle.
6 - C'est alors le retour au pointage fin suivi du régime libre, jusqu'à la prochaine désaturation.
Les simulations les plus complètes reposent sur le schéma fonctionnel suivant :
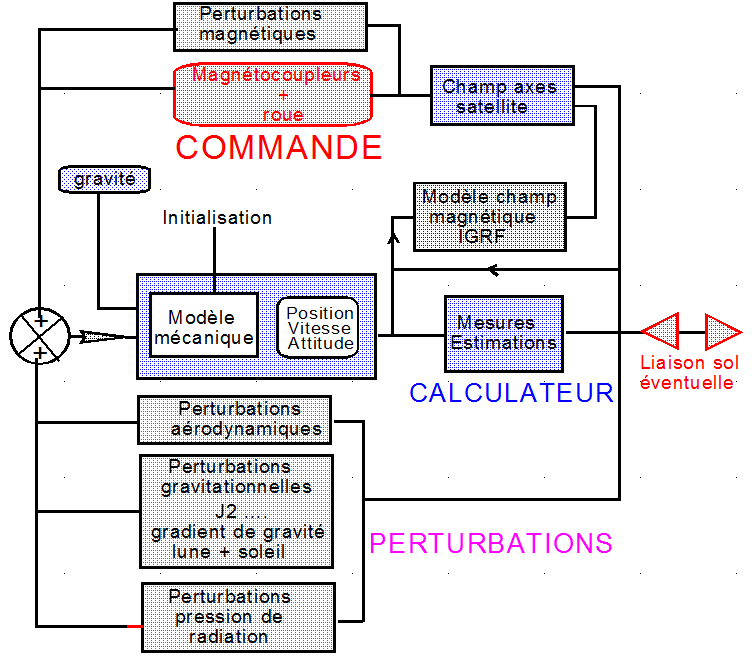
Avec:
- En bleu les modules intégrés calculant ou estimant, après traitement des mesures: position, vitesse, attitude, champ magnétique en axes satellite, connaissant le champ magnétique IGRF de référence, stocké à bord. Le calculateur et séquenceur programment en continu la commande des magnétocoupleurs et d'une roue tangage.
- En rose ce qui est considéré comme perturbations dans le vol réel, s'exerçant bien évidemment naturellement sans calcul. Ces perturbations sont cependant approchées au mieux dans les simulations de validation de la commande, et dans ce cas là ces perturbations sont dans la boucle du calculateur de simulation.
- En rouge la commande élaborée en continu par le calculateur de bord. En cours de vol certaines données peuvent être transmises au sol ou reçues du sol, pour information ou restitution d'orbite.
I AVEC LE TANGAGE SEUL POUR ESSAYER LA ROUE: Récupérer les fichiers
1°) SIMULATION LA PLUS SIMPLE :
Mise en place d'une régulation PD, uniquement sur le tangage. Sans rien, puis avec des retards dans la chaîne de mesure ou de commande, puis avec les perturbations.
|
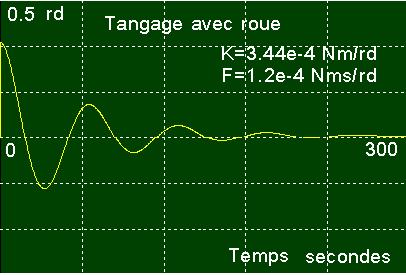
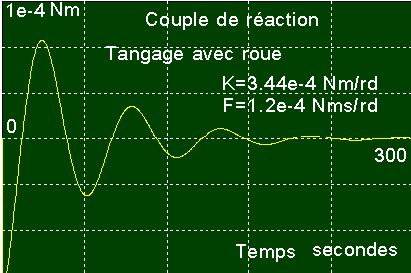
Simulation
réalisée avec Simclas1 Roue
parfaite Sans
couples autres que celui de la roue Couple roue max = 10-4 Nm |
 |
 |
|
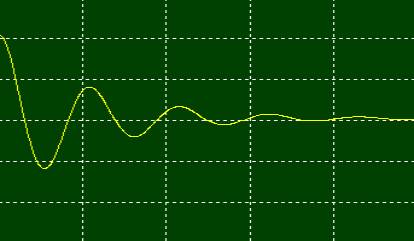
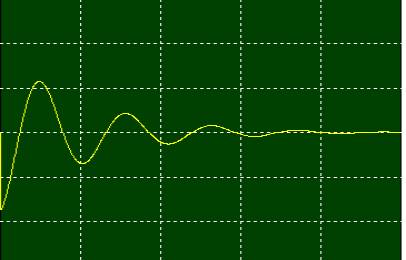
Simulation
réalisée avec Simclas2 Roue avec retard Position avec retard Vitesse
avec retard Sans
couples autres que celui de la roue Couple
roue max = 10-4 Nm Avec des retards de moins de 1 seconde, les résultats ne sont pas affectés |
 |
 |
|
Simulation
réalisée avec Simclas3 Roue
avec retard Position avec retard Vitesse avec retard Sans
couples autres que 1-
celui de la roue 2-
Un couple aérodynamique constant Couple
roue max = 10-4 Nm Avec des retards de moins de 1 seconde, les
|
La
roue, par contre tourne sans arrêt même pour celui prévu de 4 e-8 Nm,
et varie entre 0 et 1.6 e-6
Nm Comme
Jdw/dt = Caero il vient dw/dt
= 5 e-3 rd/s² w = 5 e-3 t à environ 30 radians en 6000 secondes donc par période |
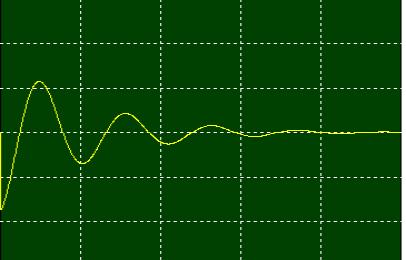
Avec
6000 tours/mn maxi, soit 630 rd/s maxi, il faut compter Une DESATURATION TOUTES LES 21 PERIODES soit 126000 secondes, environ toutes les 36 heures
|
|
Simulation
réalisée avec Simclas4 Roue
avec retard Couples
autres que celui de la roue Couple aérodynamique constant ( 4e-8 Nm ) Le couple du gradient de gravité Couple
roue max = 10-4 Nm |
L'asservissement de teta n'est que très légèrement affecté |
Le couple roue n'est que très légèrement affecté par le gradient de gravité très faible à cette altitude, pour un nanosatellite ( Max 6 e-10 Nm ) |
|
|
||
|
|
|
K_PD=8.6
e-4 Nm/rd Variation
de teta Départ
à 0.35 rd , environ 20°, à vitesse nulle Limite
à 0.1 rd Roue
vitesse initiale 10 rds Vitesse
finale 7.8 rd/s "Elle
n'a pas pris beaucoup de tours" !!! Evolution
du couple délivré par la roue, sur 700 s |
2°) SIMULATION DE LA DESATURATION :
Réalisée par simclas9.m initialisée par scaodat9.m
Voici les principaux résultats
|
|
|
|
|
|
Simulations
réalisées avec : Teta_zero
= 0.1 rd Gain
en désaturation de 8000 SI, Gain
en rappel proportionnel K_PD = 43 e-5 Gain
en rappel dérivée F_PD = 15
e-4 Déclenchement
de la désaturation à 3600 t/mn |
|
II REGULATION DES 3 AXES EN MODE POINTAGE FIN:
Voir plus loin une simulation SCADESAT bâtie sur les équations du TMC en petits angles et vitesses faibles
III REDUCTION DES VITESSES SUR LES 3 AXES EN MODE "DETUMBLING INITIAL":
Dans les 3 modes de réduction des vitesses, juste après la mise en orbite, l'usage des magnétocoupleurs est obligatoire et conduit infailliblement à la réduction des vitesses angulaires, mais pas forcément au bon pointage. C'est la phase de "DETUMBLING".
Plusieurs idées sont essayées, dont :
La première réduire les vitesses avec 3 magnétocoupleurs, sans roue ( voir 1°) utilisant la dérivée de B ( dite en Bpoint ), méthode expliquée par M DAMILANO dans une demande de brevet
D'autres, qui me sont plus personnelles, à titre d'essais, utilisant des magnétocoupleurs sur les axes roulis et lacet avec une roue sur l'axe tangage.
- Soit avec une régulation tangage s'opposant à q et au tangage ( voir 2° )
- Soit en s'opposant à q - w 0 ( car la stabilisation a tendance à faire converger q vers la rotation orbitale ) et au tangage, on dira régulation améliorée. ( Voir 3° )
Enfin, une méthode expliquée par M LAURENS dans une demande de brevet, utilisant des magnétocoupleurs sur les 3 axes, appelée méthode boussole. Plusieurs variantes ont été essayées.
1°) LA SIMULATION ( reg_derB.m initialisée par derivdat.m : | Récupérer les fichiers de simulation | Voir la théorie de la régulation avec la dérivée du champ - magnétique |
NB : Cette même simulation permet de traiter le mouvement de Poinsot et donc de vérifier qu'une bonne partie du programme est valide.
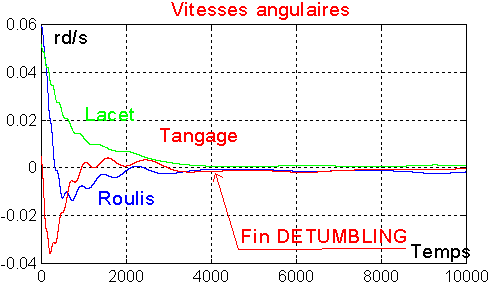
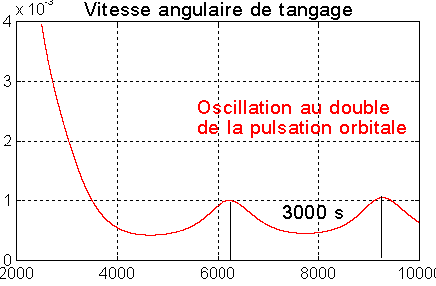
La rotation tangage tend vers une oscillation à une période moitié
de la période orbitale, soit environ 3000 secondes
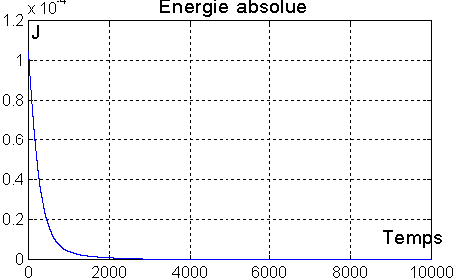
L'énergie est bien dissipée en continu. Le detumbling est terminé en
une heure environ.
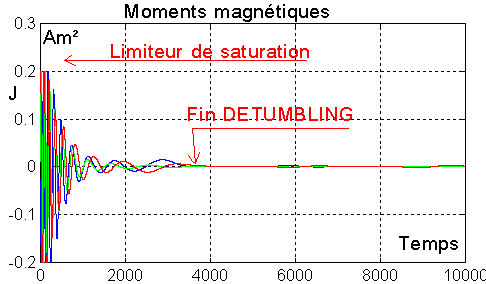
ENSEIGNEMENT A TIRER : Bien que la simulation soit convaincante, en ce qui concerne la dissipation d'énergie, qui ne fait aucun doute, elle ne suffira pas à obtenir l'acquisition d'une attitude correcte, car les angles ne sont pas ramenés près de 0. Comme le préconise M DAMILANO, il faut utiliser la roue pour "forcer" au moins le tangage à stabiliser son axe perpendiculairement au plan orbital. Ce sera l'objet des simulations regderb1, regderb2, regderb3.m avec une roue de réaction sur le tangage. |
2°) DETUMBLING AVEC CONTROLE ROULIS ET LACET PAR MAGNETOCOUPLEURS ET TANGAGE PAR UNE ROUE :
Simulation regderb1.m initialisée par derivdat.m
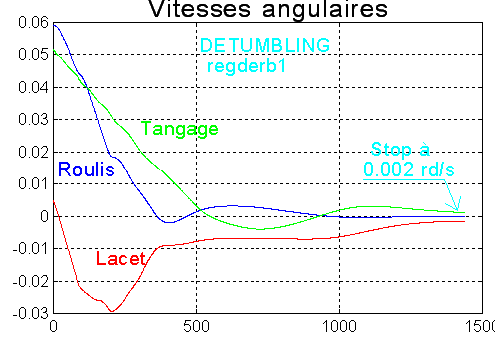
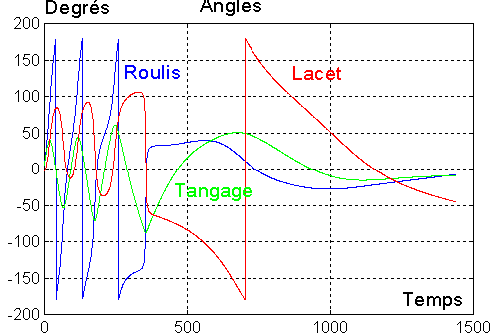
Seule la rotation transversale ( p et r ) est prise en compte pour la dérivée de B ( vitesse due à p et r ). Le tangage est traité par la roue
La roue délivre un couple avec rappel proportionnel de vitesse sur q ( et non q - w0 ), et un rappel proportionnel sur l'angle de tangage.
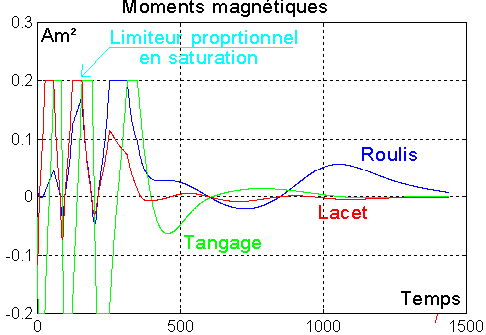
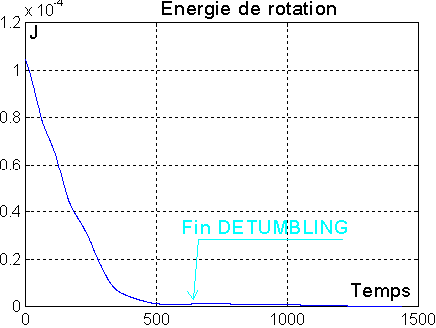
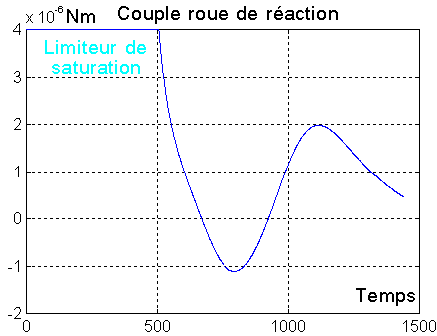
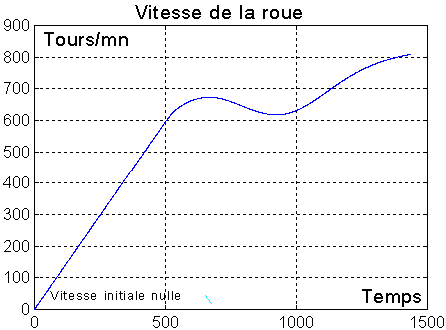
3°) DETUMBLING AVEC CONTROLE ROULIS ET LACET PAR MAGNETOCOUPLEURS ET TANGAGE AMELIORE PAR UNE ROUE
Simulation regderb2.m initialisée par derivdat.m
Seule la rotation transversale ( p et r ) est prise en compte pour la dérivée de B ( vitesse due à p et r ). Le tangage est traité par la roue, un peu différemment.
La roue délivre un couple avec rappel proportionnel de vitesse sur q - w0 , et un rappel proportionnel sur l'angle de tangage.
Résultats pratiquement identiques, ce qui doit tenir au test d'arrêt à 0.003 rd/s pour les vitesses
IV LES REGULATIONS FINALES SIGNIFICATIVES: Toutes dans nanosat0/1/2..etc....
1°) DETUMBLING "Bpoint" ( méthode DAMILANO ) avec champ pulsé déduit des mesures :
a) Avec la dérivée de B seule, optimisée par rapport aux inerties :
NANOSAT5/REGDERBP.M & DERIVDAT Voir quelques résultats |
- Fonctionne correctement, réalise la réduction des vitesses sur seuil commandé.
- N'assure pas le pointage angulaire.
- En fin de "détumbling", les angles sont aléatoirement quelconques
- Demande un autre mode pour l'acquisition grossière
- INFORMATIONS ET MATERIELS NECESSAIRES EN CONTINU :
- Les composantes mesurées du champ magnétique sur les axes satellite
- Les composantes mesurées de la dérivée du champ magnétique
- Les inerties satellite
- 3 magnétocoupleurs, pas de roue nécessaire.
- A PROGRAMMER :
- Le calcul des moments magnétiques mx_deriv, my_deriv,mz_deriv par la fonction MOM_MAGN.M
- TRANSMISSION DES DONNEES FINALES :
Par init_GP.mat ( variable init_acqGP) ou directement dans l'espace Matlab 2 variables temps_init_GP et initpqrQ_GP
par exemple temps_init_GP = 4.7003e+003 et initpqrQ_GP= [-0.0024 0.0040 -0.0029 0.2908 -0.4166 0.8205 0.2620]
b) Avec la dérivée de B , non optimisée par rapport aux inerties et un rappel sur un champ magnétique de consigne et 3 magnétocoupleurs, pas de roue:
NANOSAT1/BOUSSOL0.M & LAURDAT0 |
- Fonctionne correctement, réalise la réduction des vitesses sur seuil commandé ( 0.01 rd/s ).
- N'assure pas le pointage angulaire.
- En fin de "tumbling", les angles sont aléatoirement quelconques
- Demande un autre mode pour l'acquisition grossière
- Ne nécessite que 3 magnétocoupleurs, pas de roue dans cette phase
- TRANSMISSION DES DONNEES FINALES :
Par init_lib.mat avec comme variable d'initialisation init_pert
2°) a) DETUMBLING + ACQUISITION GROSSIERE ( Avec champ réel non pulsé ) : :
NANOSAT0/TOTALE2.M & DERIVDAT |
- Fonctionne correctement, réalise la réduction des vitesses sur seuil commandé.
- Bascule automatiquement en mode acquisition grossière
- Assure pas le pointage angulaire avec arrêt sur seuil prédéterminé.
- En fin de tumbling, les angles sont aléatoirement quelconques
- Résultats par display0
|
» *************** PRINCIPALES DONNEES DE LA SIMULATION *************** |
- TRANSMISSION DES DONNEES FINALES :
Par init_lib.mat qui stocke le temps et pqrQ,
- Avec comme variable d'initialisation init_pert_lib récupérable dans l'espace Matlab ou par le stockage:
- Le temps final d'acquisition ou de départ du régime libre temps_fin_acq
- L'initialisation du régime libre est init_pert_lib
3°) MODE LIBRE SIMPLEMENT SOUMIS AUX PERTURBATIONS ( Le champ est naturellement réel ): On le retrouve dans toutes les séquences du lancement à l'attitude de travail ( nanosat0 ... nanosat7 )
REG_PERT.M / PERT_DAT |
- Fonctionne correctement, les vitesses se mettent bien évidemment à diverger.
- Bascule automatiquement en mode acquisition fine sur un seuil angulaire
- TRANSMISSION DES DONNEES FINALES :
Par init_fin.mat qui stocke le temps et les données angles et vitesses,
- Avec comme variable d'initialisation init_fin_mat récupérable dans l'espace Matlab ou par le stockage:
- Le temps final d'acquisition ou de départ du régime libre temps_init_tmc
- L'initialisation du régime libre est etat_init_tmc
4°) MODE FIN AVEC PERTURBATIONS ( Champ réel ): On le retrouve dans toutes les séquences du lancement à l'attitude de travail ( nanosat0 ... nanosat7 )
REGDESAT.M / SCADESAT (Démonstration présentée à Marseille ) |
- Fonctionne correctement, les vitesses convergent rapidement, les vitesses restent maîtrisées.
5°) MODE FIN SOUMIS AUX PERTURBATIONS, DESATURATION : On le retrouve dans toutes les séquences du lancement à l'attitude de travail ( nanosat0 ... nanosat7 )
REGDESAT.M / SCADESAT (Démonstration présentée à Marseille ) |
- Fonctionne correctement, les vitesses et les angles sont maîtrisés durant la désaturation.
- Arrêt et départ commandés sur seuils de vitesse maximale
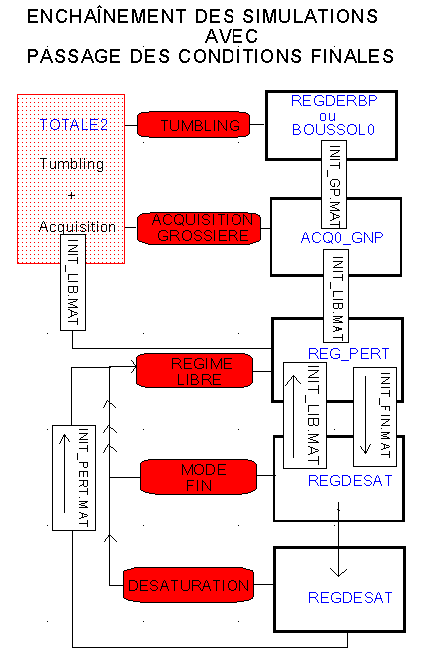
NB 0 : La suite TOTALE2 --> REG_PERT --> REGDESAT --> REGDESAT peut s'exécuter dans nanosat0 avec transmission des données.
************************************************
NB 1 : La suite BOUSSOL0 --> ACQ0_GNP --> REG_PERT --> REGDESAT --> REGDESAT peut s'exécuter dans nanosat1 avec transmission des données.
************************************************
NB 3 : BOUSSOL2 permet de réduire les vitesses rapidement avec en parallèle de la simulation de Laurens, une régulation sur la vitesse angulaire autour de B. Les angles ne peuvent donc pas être acquis. Elle s'exécute dans nanosat3
************************************************
NB 4 : La simulation BOUSSOL5 offre 3 versions possibles de régulations séparées ou en parallèle:
- une avec régulation de Laurens seule
- une avec régulation sans Laurens uniquement en PD sur les 3 angles
- une avec régulation de Laurens et régulation PD sur les 3 angles
Elle permet par récupération des valeurs finales, de simuler l'acquisition fine, puis le régime libre sous perturbations etc.. jusqu'à une désaturation éventuelle avec
--> REGACQG2 --> REG_PERT --> REGDESAT --> REGDESAT peuvent s'exécuter dans nanosat4 avec transmission des données.
************************************************
NB 5 : La suite REGDERBP ( version pulsée signifiant que les contraintes de la mesure du champ impose l'arrêt des magnétocoupleurs) ou REGDERB ( version non pulsée ) ---> REGACQG2 ---> REGDESAT --> REGDESAT peuvent s'exécuter dans nanosat5 avec transmission des données.
On observera que lorsque By = BY les courbes réagissent nettement
************************************************
NB 6 : La suite REGDERB1 ( version non pulsée ) ---> REGACQG2 ---> REGDESAT --> REGDESAT peuvent s'exécuter dans nanosat6 avec transmission des données.
On observera que lorsque By = BY les courbes réagissent nettement
************************************************
NB 7 : La suite REGDERB3 ( version non pulsée ) ---> REGACQG2 ---> REGDESAT --> REGDESAT peuvent s'exécuter dans nanosat7 avec transmission des données.
***********************
Fin de page *************************