EQUATIONS DE LA DYNAMIQUE D'UN SATELLITE

AVEC UTILISATION DU QUATERNION D'ATTITUDE

QUATERNION D'ERREUR POUR UN SCA

Le lecteur qui aura déjà parcouru ce mini site consacré au SCA d'un nanosatellite, a donc pris contact avec le SCA du cas petits angles.

Pour une mise au courant voir les données de base de la mission.

Les approches soit avec le TMC ou le formalisme lagrangien, ont permis de se familiariser avec l'utilisation d'une roue de réaction et des magnétocoupleurs. Cependant, le premier défi à relever est celui de la maîtrise de la dynamique du satellite dans les conditions aléatoires de la mise en orbite, face à des vitesses élevées et des angles turbulents. Le concept petits angles n'est plus utilisable et nous devons impérativement avoir recours au quaternion d'attitude du satellite.

La page se limite à une mise en  orbite circulaire.

I REPERES DE TRAVAIL :

Rappelons brièvement que tout repérage à base d'angles présente des configurations spéciales où un angle n'est pas défini, entraînant des difficultés de programmation ou de continuité de cet angle.

La question ne concerne que la connaissance de l'attitude d'un satellite, ici un nanosatellite, par rapport à un repère de consigne ou de travail.

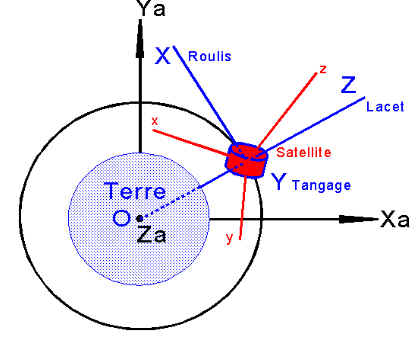
Xa Ya Za un repère absolu ou inertiel.

CHOIX DU REPÈRE ORBITAL: 

XYZ est le repère de consigne, pour nous en pointage zénith, le repère orbital est: X suivant la vitesse, Y suivant le moment cinétique orbital et Z le zénith.

Mais si on souhaite un pointage nadir, il est aussi possible de choisir le repère orbital mieux adapté à cette attitude, notamment pour garder l'équilibre avec des valeurs nulles des angles. On prendra alors X suivant la vitesse orbitale, Y de sens contraire au moment cinétique orbital et Z suivant la verticale descendante.

xyz est un repère lié au satellite, adapté à sa géométrie. Ci-dessous le repérage par angles de Cardan. q le tangage, F le roulis et y le lacet

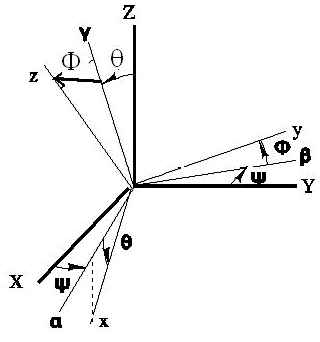
II EQUATIONS DE LA DYNAMIQUE AVEC QUATERNION :

Le satellite peut être équipé d'une roue de réaction, sur l'axe tangage y,  d'inertie J et de vitesse angulaire ( relative au satellite ) w.

On note W, w, Q, C, Cm respectivement la rotation absolue du satellite, la rotation de la roue par rapport au satellite, le quaternion d'attitude du satellite ( ou encore du repère xyz qui lui est attaché, par rapport au repère orbital XYZ), le couple résultant des actions externes, le couple moteur interne de commande de la roue.

w₀  désigne la rotation orbitale, pour nous constante sur une orbite circulaire. Le comportement du quaternion est donné sur ce site. Voir page dédiée

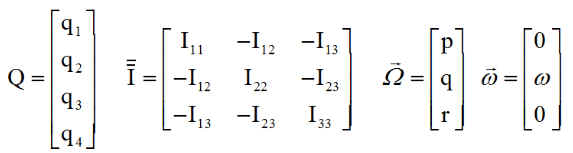
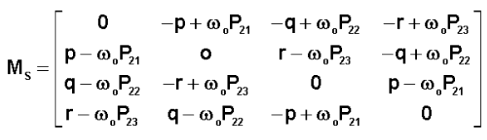
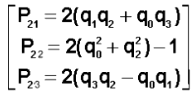
On obtient alors les 8 équations du mouvement, formant un système fermé pour le calcul de ( p q r q₁ q₂ q₃ q₄ w )

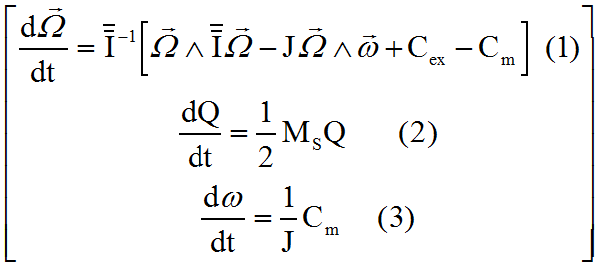
 (1) donne la rotation instantanée absolue du satellite, avec au second membre :

- Cex le couple externe comprenant toutes les perturbations, y compris le gradient de gravité ( voir le calcul du gradient avec le quaternion )

- Cm le couple action de commande programmée du satellite sur la roue, qui agit comme une réaction

- On aura reconnu les termes de couplage interne au satellite

- On aura reconnu les termes de couplages roue-satellite

 (2) donne le quaternion d'attitude du satellite en axes orbitaux X Y Z, avec lequel on pourra retrouver les angles de Cardan ou d'Euler

 (3) fournit le comportement de la vitesse angulaire de la roue, vitesse à surveiller pour le respect des contraintes techniques.

NB : Je conseille à l'utilisateur du quaternion d'attitude de se renseigner sur sa normalisation à opérer en continu, au cours de l'intégration des équations.

III CRITERES DE VERIFICATION :

Il est possible de vérifier qu'une bonne partie d'une programmation éventuelle est correcte en prenant le cas particulier Cm = 0, Cex = 0

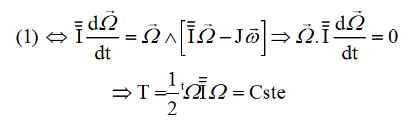
C'est la conservation de l'énergie cinétique. Par ailleurs les équations devraient conduire vers le MOUVEMENT DE POINSOT, avec notamment la conservation du vecteur moment cinétique et de sa norme en particulier. Ces vérifications sont aisées en cours de simulation.

IV QUATERNION D'ERREUR DANS UNE REGULATION :

Nous l'avons vu, l'avantage de l'utilisation du quaternion d'attitude Q représentant la rotation qui amène le repère orbital XYZ sur le repère satellite R, est de s'affranchir de toute singularité angulaire ( angles de Cardan ou d'Euler )

On peut donc imaginer un contrôle s'appuyant, comme tout contrôle, sur un quaternion d'erreur à définir.

1°) Position réelle :

Bien évidemment jamais connue.

quaternion réel

2°) Position estimée :

Si le satellite est équipé d'une restitution d'attitude, les divers senseurs vont donner une position entachée d'erreurs, qu'un filtrage de Kalman va traiter, pour fourni la meilleure position estimée ( le chapeau ^ sera utilisé pour ce qui concerne les notions estimées). 

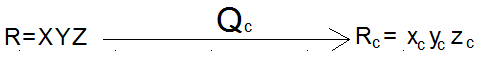
quaternion estimé

3°) Position visée ou repère cible

Rc est le repère de position idéale de travail, que la régulation doit chercher à faire atteindre au repère satellite R et surtout au repère position estimée.

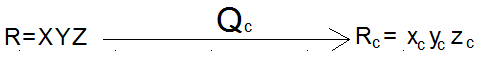
quaternion cible

4°) Quaternion d'erreur :

Tout naturellement c'est le quaternion faisant passer de la position estimée à la position cible.

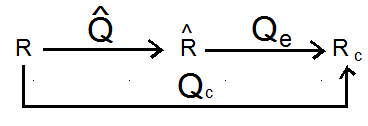
Qe quaternion d'erreur

Un calcul simple donne :

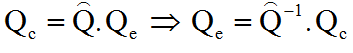
V EXPLOITATION DU QUATERNION D'ERREUR POUR UNE RÉGULATION PD :

Classiquement, le quaternion d'erreur peut être l'entrée dune boucle de commande, avec rétroaction, pour le calcul d'un couple de commande sur le satellite.

La connaissance du quaternion d'erreur donne :

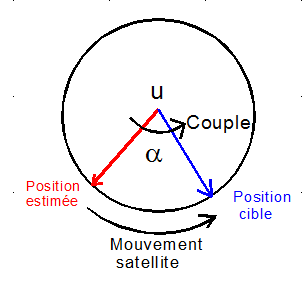
- L'axe u de la rotation du quaternion d'erreur, par sa partie vectorielle

- l'angle a de cette rotation. La convention choisie est 0< a < p.

Nb: Si en cours de calcul,  a < p , alors on change a en 2p - a et le vecteur u en -u. Ce qui amène toujours l'estimation vers la cible avec une rotation entre 0 et 180°.

Logiquement, le couple de commande doit agir pour réduire l'angle a et conjointement aussi la vitesse angulaire du satellite, la commande agit donc :

- Proportionnellement à l'angle a , et dans le même sens, donc avec un coefficient Kp > 0, en effet contrairement à l'habitude, pour un rappel, dans le cas présent une rotation dans le même sens que a rapproche l'estimation de la cible.

- Proportionnellement et en sens contraire du vecteur rotation relatif W du satellite par rapport au repère orbital,  ceci pour stabiliser le satellite en mode dissipatif, le coefficient est alors Kd > 0.

La commande s'écrit donc :

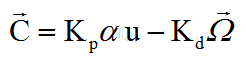
RAPPEL : voir page spéciale

Le vecteur rotation du satellite par rapport au repère orbital a pour composantes en axes satellite:

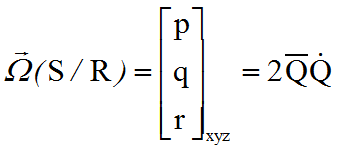
*****************************  Fin de la page  **********************************

Septembre 2014