I LA FONCTION DE LAGRANGE :

NB : Nous n'étudions pas le mouvement exact, mais les mouvements du pointage fin dans lequel paramètres et dérivées sont supposés rester petits. Nous devons ne conserver que les termes infiniment petits d'ordre maximum 2 que ce soit en dérivées ou en paramètres ou en termes croisés dérivées et paramètres. Ceci pour aboutir à des équations de Lagrange linéarisées d'ordre 1.

Rappel : Dans le formalisme lagrangien, la fonction de Lagrange de  notre satellite  doit apparaître sous sa forme la plus générale 

nous savons que f(t) peut être omise.

1°) ENERGIE CINETIQUE :

a) Exacte :

Classiquement, nous calculons l'énergie cinétique par :

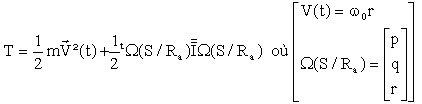
nous pouvons "oublier" le premier terme, uniquement fonction du temps, pour ne garder que l'énergie absolue de rotation. avec le vecteur rotation instantanée absolue exact déjà calculé ailleurs:   

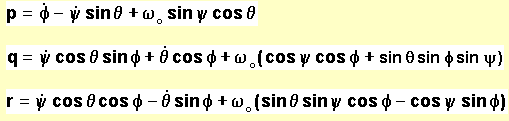
b) Linéarisation pour des amplitudes faibles:

NB : Ce calcul est à conseiller à tout étudiant mécanicien théorique, car il est source de tous les pièges associés aux DL et au calcul d'une énergie simplifiée lors de petits mouvements.

En effet, il faut ne pas oublier que nous cherchons un équivalent de l'énergie cinétique à l'ordre 2 par rapport aux angles et leurs dérivées. Or, la composante q est très spéciale, car elle pourrait simplement s'écrire ( à première vue )

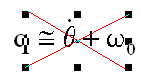
ce qui conduit à une erreur. En effet, dans l'énergie cinétique, c'est q² qui est à considérer et qui doit conserver les termes d'ordre 2. Comme q contient une constante, il faut garder les termes d'ordre 2, qui vont donner dans le double produit du carré des termes encore d'ordre 2. Il en est de même avec le produit pq qui contient un w₀ dans une parenthèse nécessitant de garder un deuxième dans l'autre c'est à dire p. Pas évident !!!!

Donc pour viser le deuxième ordre final :

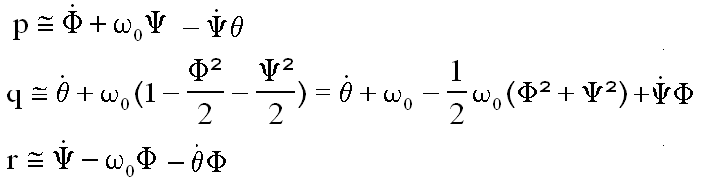
Remarque : je m'attends à ce qu'on me dise que dans l'expression de q j'ai conservé 2 termes d'ordre 2 à coté d'un terme d'ordre 1 et 1 d'ordre 0. C'est un problème classique dans les DL, car ce qui compte c'est l'approximation finale qui elle est limitée à l'ordre 2 et 2 maximum, dans l'énergie cinétique.

Or nous aurons à calculer q²  expression suivante:

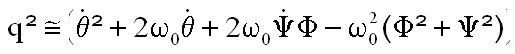
ainsi que pq et qr ( vous ferez le calcul )

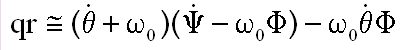
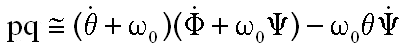
NB : Exemple à méditer longuement, quand on linéarise des équations !!!! 

Finalement l'énergie cinétique réduite utile à celle de rotation, dépouillée des termes inutiles s'écrit sous la forme condensée déduite de :

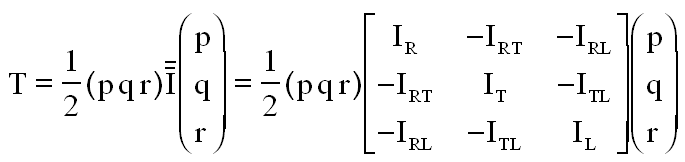
Le lecteur achèvera ces calculs, pour trouver, compte tenu de q² et des termes à conserver, cette expression de l'énergie simplifiée  

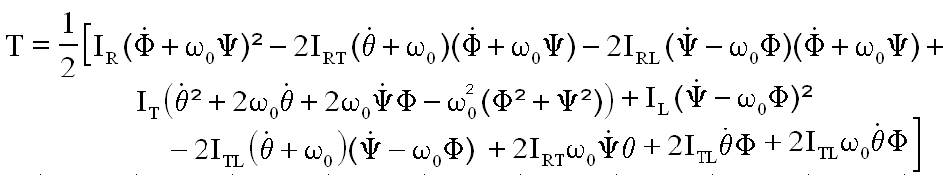
1°) ACTIONS EN JEU :

Dans les "actions" en jeu, nous trouvons :

- Gravitation classique , c'est un terme uniquement fonction du temps, qui ne dépend que du mouvement orbital, dont la résulante n'intervient pas dans la rotation.

- Le couple gradient de gravité, avec 2 termes:

La partie principale classique, mais un autre terme, avec les produits d'inertie, qui peut avoir son importance quand la matrice d'inertie n'est pas diagonale. En général, on veille, pour les gros satellites, à avoir une matrice d'inertie diagonale par rapport aux axes satellite importants.

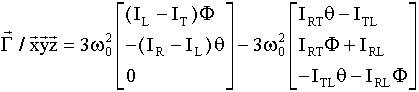
nous le traiterons comme une perturbation.

- Les couples  perturbateurs que nous résumerons en un seul couple noté Cpert

Ces actions apparaîtront au second membre des équations de Lagrange comme coefficients des variations élémentaires des paramètres, dans le travail virtuel

2°) CALCUL DES COEFFICIENTS DU TRAVAIL :

Calculs et notations connus du lecteur

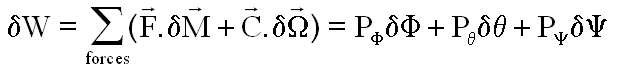
avec encore des subi lités( pas évidentes du tout ) pour les rotations virtuelles, car le formalisme lagrangien spécifie bien que les déplacements virtuels doivent être calculé à temps bloqué ( obstacles ou moteurs ou entraînement orbital bloqués), donc la rotation virtuelle n'est pas ( formule barrée)  :

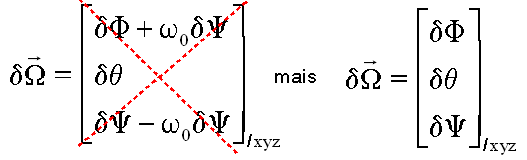
Le calcul des coefficients du travail en est simplifié :

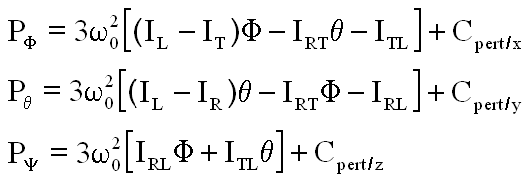
II LES EQUATIONS DE LAGRANGE DU SATELLITE SANS ROUE :

Allégeant ma rédaction, je laisse le lecteur traduire les 3 équations de Lagrange

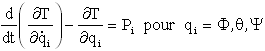
pour trouver et finir l'écriture condensée suivante où

III QUELQUES COMMENTAIRES: :

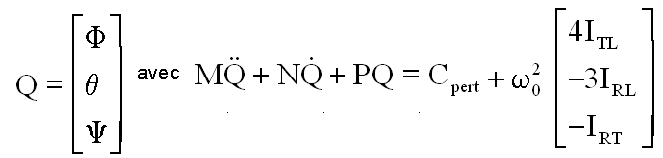
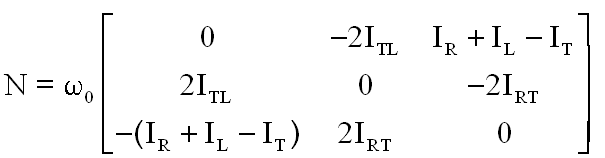
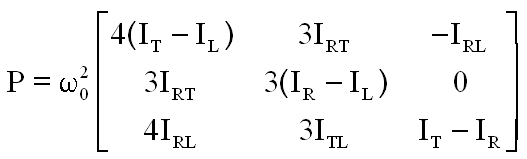
a) Sur les matrices :

- M n'est autre que la matrice d'inertie donc inversible

- N est une matrice antisymétrique, représentant en général des couplages entre les axes ou des actions dissipatives( absentes dans le cas envisagé ) . 

- P est une matrice hybride, montrant sur la diagonale des rappels de type élastique ( gradient principal ), et des termes provenant de couples inertiels ( puisque nous travaillons en axes mobiles ) donc pour la stabilité au regard du gradient de gravité :

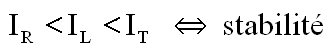
C'est le choix de notre nanosatellite, bien qu'à 817 km du sol le gradient de gravité ne soit pas très efficace.

b) Note personnelle de calcul:

Comme je ne suis plus très pointu sur les calculs, je préfère m'entourer de vérifications, utiles d'une part pour les calculs, d'autre part pour valider une simulation sur un cas particulier.

Je fais donc un calcul classique de mécanique lagrangienne --> la sommation de la combinaison linéaire des premiers membres par les dérivées premières des paramètres du système. Rapide rappel sans commentaires:

Partant des équations de Lagrange 

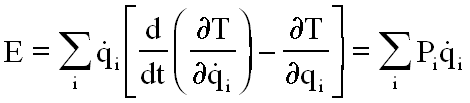
Classiquement, on décompose l'énergie cinétique en partie quadratique T2, linéaire T1 et "constante T0 dénominations par rapport aux variables dérivées.

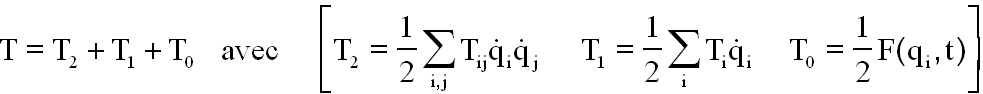
Le lecteur sait ou montrera ( utiliser les propriétés des fonctions homogènes )que

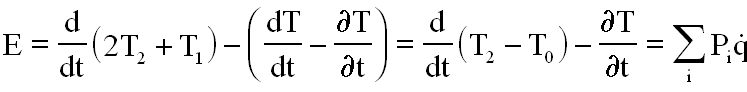
Si de plus les actions extérieures dérivent d'un potentiel, c'est à dire

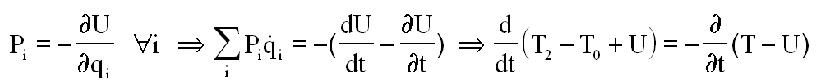
Pour conclure, si la fonction de Lagrange ne dépend pas explicitement du temps on a une loi de conservation, dite " Intégrale première de Painlevé"

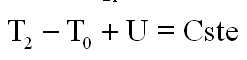
OUTIL DE VERIFICATION : Bien sur toutes les configurations ne peuvent pas être vérifiées, mais la programmation peut être validée en partie, sur un cas particulier, ce qui peut rassurer.

On suppose le nanosatellite avec une matrice d'inertie un peu plus simple ( pour enlever les termes parasites du gradient ), le lecteur calculera le potentiel associé au termes restants.

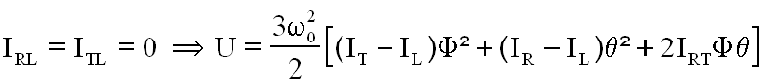
La loi de conservation de Painlevé se traduit par

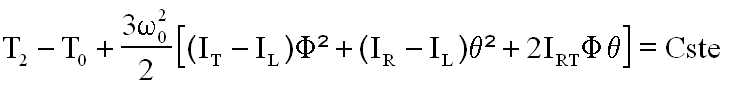
La vérification se fait donc sur cette expression :

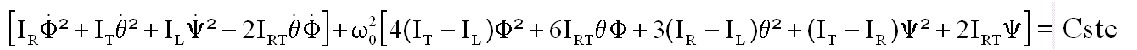
AUTRE MANIERE : On reprend le système différentiel sous forme matricielle et on multiplie à gauche par la matrice transposée des dérivées:

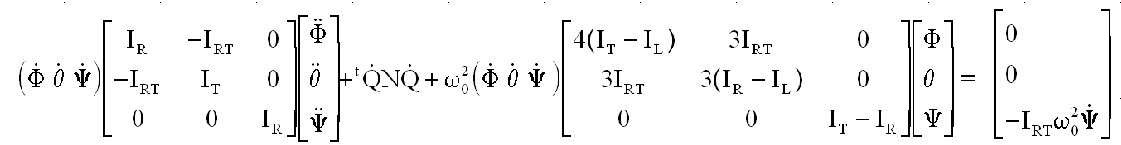
N antisymétrique entraîne la nullité du terme central et par intégration on obtient la même intégrale première.

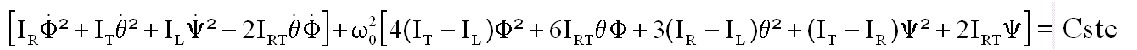
IV LES EQUATIONS  DU SATELLITE AVEC ROUE :

La roue de réaction disposée sur l'axe tangage a un moment d'inertie J et une vitesse angulaire w variable ( sur commande du contrôle d'attitude satellite ).

Pour le calcul de l'énergie cinétique de tout le système ( satellite + roue ) il suffit de rajouter le seul terme relatif à don axe, et ne concernant que w, soit

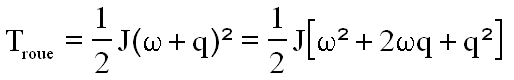
Le terme en q² est déjà pris en compte avec l'énergie satellite roue bloquée.  Donc il reste

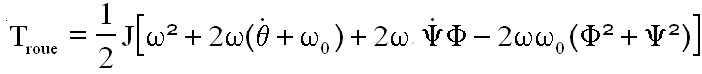
Reprenant les équations de Lagrange une par une, le lecteur ajoutera les termes suivants au premier membre de chaque équation

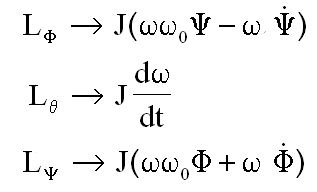
Voir la suite de la mise en équations

*****************************  Fin de la page  ********************************