Voir la mise en équations initiale

I LES EQUATIONS  DU SATELLITE AVEC ROUE :

La roue de réaction disposée sur l'axe tangage a un moment d'inertie J et une vitesse angulaire w variable ( sur commande du contrôle d'attitude satellite ).

Pour le calcul de l'énergie cinétique de tout le système ( satellite + roue ) il suffit de rajouter le seul terme relatif à son axe, et ne concernant que w, soit 

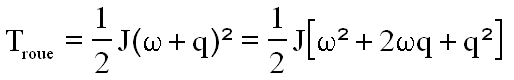
Le terme en q² est déjà pris en compte avec l'énergie satellite roue bloquée.  Donc il reste

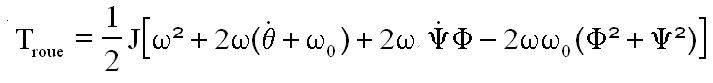
Reprenant les équations de Lagrange une par une,

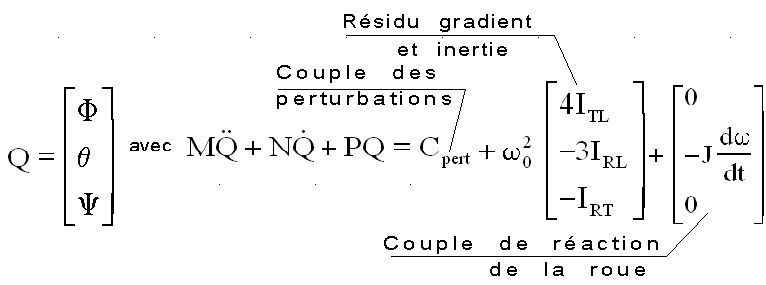
le lecteur ajoutera les termes suivants au premier membre de chaque équation

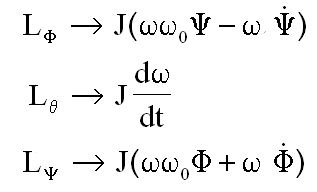
Pour obtenir :

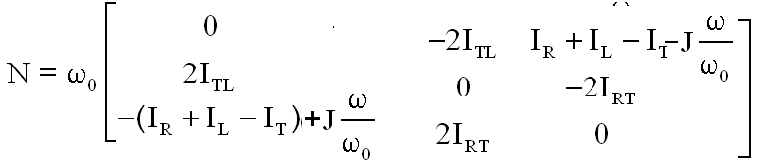
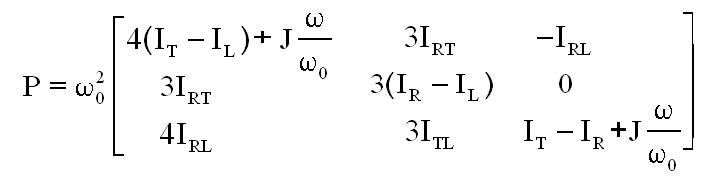
COMMENTAIRE :

Les équations sont strictement les mêmes qu'avec le TMC, mais à quel prix, pour les calculs et les précautions.

II MISE SOUS FORME CANONIQUE : : Ce travail a déjà été réalisé ailleurs

La matrice M qui n'est autre que celle d'inertie est donc inversible. Ce qui permet d'écrire le système sous la forme :

NB : on pourrait avoir pour les matrices B, D, U d'autres dimensions, suivant qu'on considère l'entrée à 3 ou 6 composantes ( les 3 dernières nulles ).

III POSITION D'EQUILIBRE :

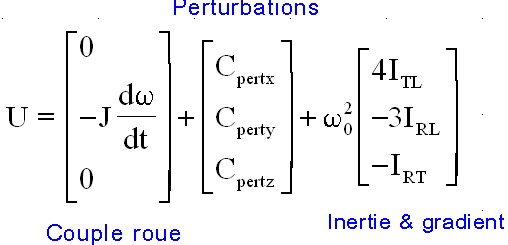
Nous supposons que seul le gradient de gravité est actif sous sa forme la plus complète et que la roue est à vitesse constante w. Nous cherchons si un équilibre est possible. Le lecteur vérifiera qu'un équilibre vérifie

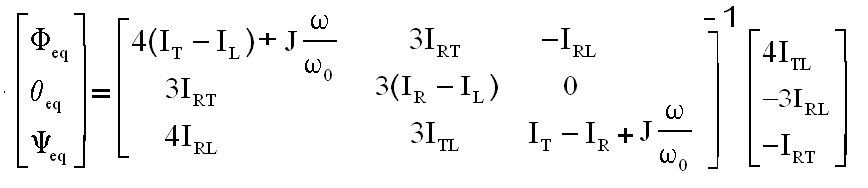
La présence de termes constants au second membre, indique qu'une position d'équilibre où les angles seraient nuls, est impossible. Ceci à cause des produits d'inertie.

De plus la position d'équilibre dépend fortement  de la vitesse w de la roue, qui peut varier de 0 à 6000 t/mn soit de 0 à 628 rd/s .

Nous savons que la rotation orbitale vaut environ 1e-3 rd/s, que J = 3.2 e-5 kgm², 4( I_T-I_l )= 56 e-3 kgm². Pour w>5 tours/s, on a 

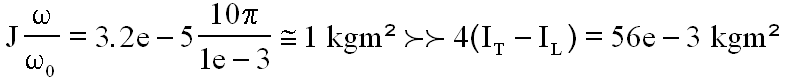
Dès que la roue tourne la matrice les éléments de la matrice d'inertie deviennent négligeables devant celui amplifié de la roue et la position d'équilibre est sensiblement  

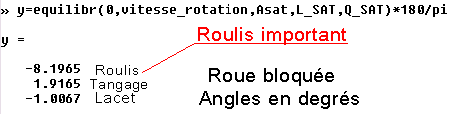
d'autant plus proche de ( 0 0 0 ) que la roue tourne vite. Pour 6000 tours/mn, = 200 p rd/s, on a en exécutant la fonction equilibr.m : 

y=equilibr(vit_roue,vitesse_rotation,Asat,L_SAT,Q_SAT);   

Sans roue, la position est très différente : roulis =0.1395 rd soit 8°, tangage =1°,2 et lacet = 3°,7 . ce ne sont pas des valeurs anodines et il faudra compter avec elles pour choisir au mieux les valeurs de consigne, pour éviter que la roue ne fonctionne pas trop en continu. En pratique, il y a des chances que l'équilibre soit très "mou" et donc peu pénalisant pour la régulation.

CONCLUSION :

Il vaudrait quand même mieux avoir une matrice d'inertie principale diagonale.

AFFAIRE A SUIVRE? Pour lancer cette fonction, il faut d'abord avoir les données dans l'espace Matlab, donc par exemple lancer l'initialisation equi_dat.m ( dans ce même répertoire, avec la fonction )avec des valeurs non nulles des produits d'inertie.

 function y=equilibr(vit_roue,vitesse_rotation,Asat,L_SAT,Q_SAT);

% Cette fonction calcule la position d'équilibre du nanosatellite libre de tout couple
% externe à part le gradient de gravité et la roue

P_SAT=L_SAT+vit_roue*Q_SAT;

Irt=Asat(1,3);Itl=Asat(2,3);Irl=Asat(1,3);

M=[2*Itl*vitesse_rotation^2 -3*Irl*vitesse_rotation^2 Irt*vitesse_rotation^2];

sys=inv(P_SAT)*M';

y=sys;

end