![]()
COMMANDE DE REGULATION PAR
"EFFET BOUSSOLE"
+
( CONTRÔLE DE L'ANGLE DE ROTATION
AUTOUR DE L'AXE DU QUATERNION )
![]()
On rappelle les relations de base de Laurens, précisées dans la théorie
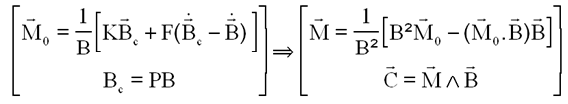
1°) MISE EN PLACE :
Lorsque la régulation de Laurens a rapproché Bc de B, alors l'axe unitaire de la rotation quaternion est très proche de l'unitaire de B, les angles sont quasiment stabilisés.
Cependant, la position de R par rapport à R0 est quelconque, avec des vitesses angulaires faibles ou très faibles. En pratique, R est quasiment fixé dans R0 et il ne reste plus qu'une rotation à faire soit autour de l'axe de B soit autour de celui du quaternion. Ces 2 axes sont très voisins. L'expression du quaternion permet de récupérer:
- L'angle de rotation b
- L'axe unitaire u de cette rotation
Une rotation d'angle b autour de l'axe u du quaternion Q, amène R sur R0.

On peut donc essayer l'application, au satellite, d'un couple C d'axe u en régulation PD ( proportionnelle-dérivée ), soit
![]()
Pour ce faire on peut utiliser une technique déjà éprouvée, indiquant qu'avec une roue de tangage et 2 magnétocoupleurs sur les axes roulis x et lacet z, on peut réaliser n'importe quel couple C ( sauf cas très particulier ). On notera Cr le couple roue sur l'axe y et M ( mx 0 mz ) les moments magnétiques des 2 magnétocoupleurs. On rappelle le résultat ( au coefficient multiplicatif By près qui a été omis )
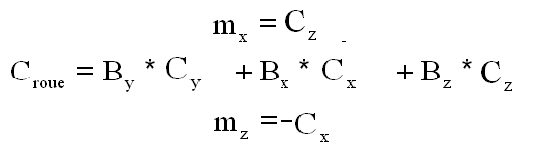
On notera que
![]()
Les moments magnétiques et le couple roue seront classiquement plafonnés par une loi conservant la proportionnalité.
2°) SIMULATION :
La simulation se déroule en 2 temps : Récupérer les routines ( un seul répertoire )
1 - Une régulation de Laurens, secondée par un traitement de la rotation autour de B, comme plus haut, avec
NANOSAT8/REGBOUX2.M & LAURDAT1.M
Les données finales, après action d'un STOP à la précision de 5° entre les unitaires de Q et de B, sont transmises à la régulation suivante 2
2 - La régulation du contrôle de la rotation autour de Q qui amène R sur R0 avec
NANOSAT8/REGBOUX6.M & LAURDAT5.M
Ceci en gardant en parallèle ( question à discuter !!! ):
a) la régulation de Laurens sans contrôle de la rotation autour de B
b) la régulation PD présentée plus haut.
3°) RESULTATS :
Apparemment satisfaisants et ressemblant beaucoup à ceux de Laurens.
a) Vitesses angulaires
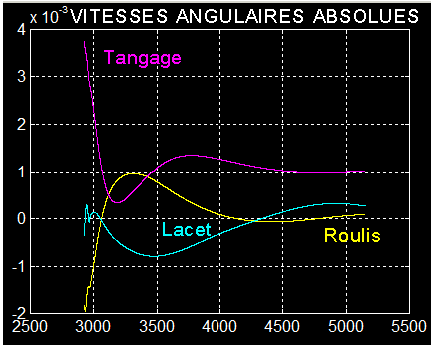
Elles tombent largement sous le seuil de 0.06 °/s, et ce qui est très rassurant celle de tangage s'aligne sur la rotation orbitale de 0.001 rd/s
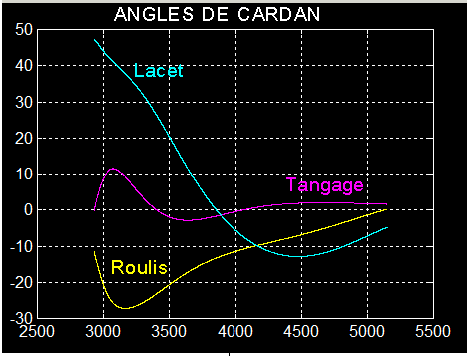
a) Angles de Cardan
Ils passent tous les sous le seuil de 5°, en moins de 4300 secondes ( Injection vers 1200 s et acquisition fine à 5500 s )
Dans mon exemple le lancement a lieu aux hautes latitudes et l'acquisition se produit après avoir survolé le pôle sud avant d'atteindre à nouveau l'équateur.
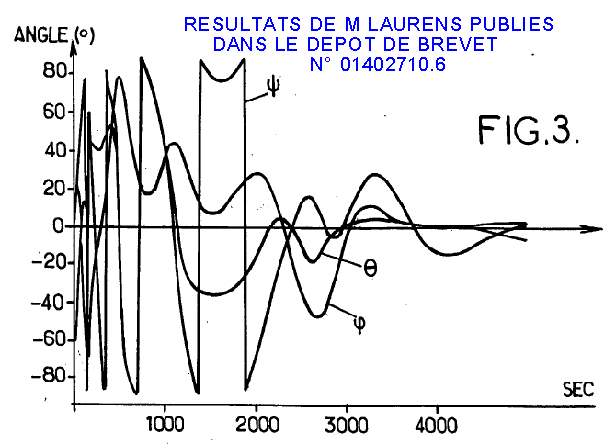
Le brevet déposé par Philippe LAURENS, donne une allure du résultat de la régulation, résultat que j'ai repris ci-dessous. Ce que nous trouvons y ressemble étrangement, à ceci près que les conditions initiales n'y sont guères lisibles et que sa simulation rassemble les deux miennes. Le résultat est très similaire.
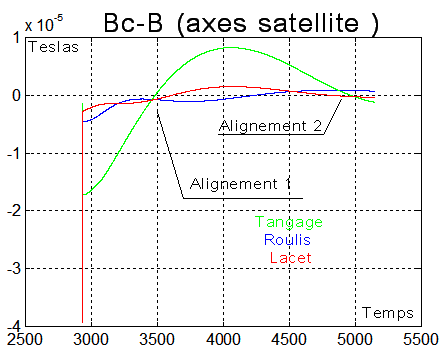
Graphe montrant 2 instants où Bc et B sont quasiment confondus
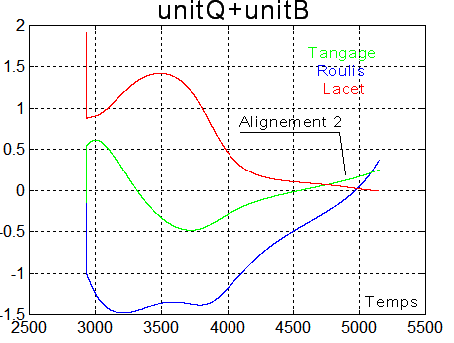
Les vecteurs unitaires du quaternion et du champ sont presque
opposés à l'alignement 2, les angles ont été ramenés presque à 0
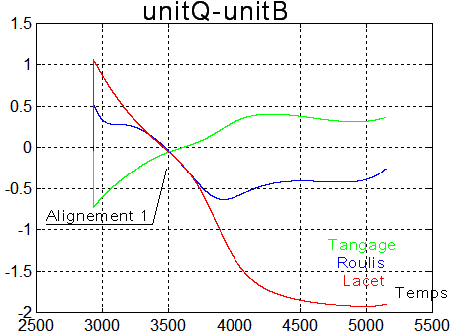
Les vecteurs unitaires du quaternion et du champ sont presque
alignés au point 1, sauf que les angles ne sont pas corrects

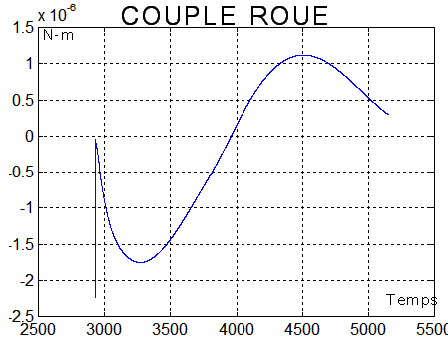
Couple exercé par la roue sur le satellite, ce qui explique
les variations de la vitesse qui paraissent être contraires
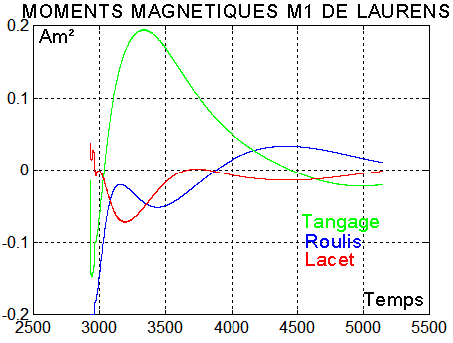
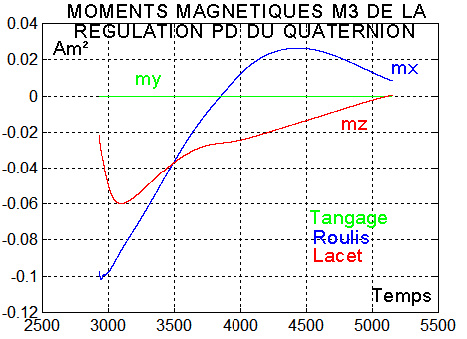
Voir aussi, un point de vue voisin avec la notion de quaternion d'erreur.
********************* FIN DE LA PAGE ********************