SOLUTION : LANCEUR L3S |
I PREMIERS INSTANTS DU VOL :
1°) Calculer l'accélération réelle au décollage, puis l'accélération statique.
Seules forces en jeu : la poussée au décollage de 241.16 tonnes ( à convertir en N ) et la pesanteur. La masse au moment du décollage est de 199.53 tonnes. La loi fondamentale fournit donc l'accélération absolue( verticale dans le cas présent ) et l'accélération statique:

NB
: Vous remarquerez, contrairement à ce que l'on pense généralement, que l'accélération au décollage est très faible et permet juste de décoller la e lanceur du sol.2°) Premières secondes du vol, vitesse relative V et altitude Z en fonction du temps. Application numérique t = 20 s
Le débit du premier étage est de 1000 kg/s, permettant d'avoir la loi d'évolution de la masse :
M(t) = M(0)-qt = 199530 - 1000 t
L'impulsion spécifique au sol vaut (Isp1)sol = 241.16 s = 2365.78 m/s
La vitesse évolue suivant la loi logarithmique du rapport de masse
l(t) et de la pesanteur :
L'altitude s'obtient par intégration de la vitesse, calcul classique avec des connaissances de DEUG. On trouve :
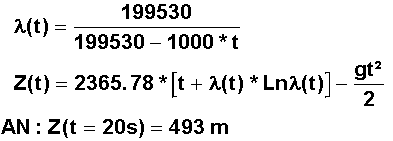
Remarque
: A postériori, on peut justifier les approximations et notamment celle sur Ispsol.II A PROPOS DE LA POUSSEE :
1°) Exprimer la poussée du premier étage, en fonction de la seule variable pa(Z).
Nous partons de la relation donnant la poussée d'un moteur fusée en vol atmosphérique :
F(Z)=q* Isp(Z)+Se*[Pe - pa(Z)] où pe est la pression ambiante, q le débit massique, Ve la vitesse d'éjection et pa(Z) la pression ambiante, qui est variable en fonction de Z.
Fvide = Fsol + Se*Pe , d'où l'expression de F(Z) = Fsol - Se*Pa(Z)
mais comme Fsol = Fvide - Se*pa(0),il vient Se = (Fvide-Fsol)/pa(0) et en conclusion :
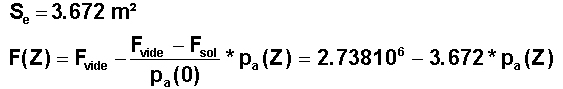
A quelle altitude atteint-elle 95% de sa valeur maximale
?Le calcul donne pa(Z) = 3.728 104 Pascal et par essais des diverses lois, on trouve Z(95%) = 7.48 km
2°) Fin de combustion de l'étage : Calculer l'accélération réelle du lanceur suivant son axe longitudinal, puis l'accélération statique.
Une figure éclairera le propos :

Si l'incidence de vol est nulle, c'est que la pente du vecteur vitesse est aussi de 26°, donc la traînée qui s'oppose à la vitesse relative est de sens contraire à l'axe lanceur X.
A 47 km la pesanteur ne vaut plus que 9.667 m/sē, la masse du lanceur n'est plus que de 59.53 tonnes,
Gl accélération longitudinale réelle Gs statique valent :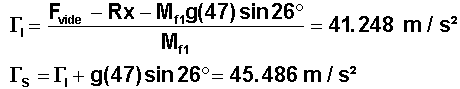
III PERFORMANCES LANCEUR :
1°) Impulsion spécifique moyenne de l'étage 1.
Savons que l'impulsion spécifique du moteur 1 est variable et empêche donc un calcul d'intégration "à la main". Conformément au cours, on fait l'approximation d'une impulsion spécifique constante égale à la valeur moyenne des impulsions spécifiques sol et vide. Le lecteur trouvera
(Isp1)moyenne = Isp1m = 260.12 s ou 2551.178 m/s valeur que nous utilisons en m/s plutôt qu'en seconde
D
Vprop1 délivré par le premier étage.Le rapport de masse de l'étage 1 est l1 = 199.53/(199.53-140)=3.3517554, donnant un incrément de vitesse propulsif DV1= Isp1m Ln(l1) donc DV1 = 3085.61 m/s
2°) Performance propulsive totale et idéale du L3S :
Le lecteur établira sans difficulté :
D
V2= Isp2 Ln(l2) = 2795.85*Ln(43.87/13.87) = 3219.4 m/sD
V3= Isp3 Ln(l3) = 4120.2*Ln(9.92/2.84) = 5153.3 m/sLa performance totale du L3S s'établit donc à 11458.3 m/s, nous dirons DVprop = 11460 m/s
3°) Estimation des pertes de vitesse subies par le lanceur :
- Un tir équatorial avec injection à 200 km permet de dire que la vitesse est vers l'Est, et horizontale ( injection au périgée ), donc le tir est PLEIN EST et bénéficie entièrement de la vitesse d'entraînement de la terre à 200 km, soit
Vet = 2*
- Une trajectoire GTO signifie un apogée à 42164 km du centre de la Terre, une injection au périgée, à 200 km du sol, permet de calculer la vitesse absolue d'injection au périgée :
2a = 6378+200+42164 = 48742 km, l'énergie vaut donc E = - 8.1777522 kmē/sē, et la vitesse au périgée vaut donc Vp = 10.239 km/s = 10239 m/s
- Avec la coiffe larguée 100 s après l'allumage du deuxième étage on gagne 50 m/s sur la performance calculée ci-dessus de 11460 m/s.
D
Vpertes = DVprop - Vp + Vet + 50 donnant DVpertes = 1749.4 m/s, nous dirons DVpertes =1750 m/sNous rappelons que la partie la plus importante de ces pertes provient de la pesanteur, puis à un moindre degré de la traînée et enfin pour une part minime des contraintes de guidage et pilotage.
![]()
Guiziou Robert février 2002