|
EQUATIONS DE CLOHESSY-WHILTSHIRE ET RENDEZ-VOUS SPATIAL |
![]()
![]()
Le rendez-vous spatial a été l'une des grandes étapes de la conquête spatiale. Mis au point, peu de temps après les premiers vols humains, il permet à l'homme de récupérer et réparer un satellite en orbite, de ravitailler une station orbitale et de réaliser des remplacements d'astronautes à bord de ces stations(Mir en fût un exemple).
Personne n'a également oublié les missions lunaires et notamment les rendez-vous tous réussis du LM( Lunar Module) avec ses deux passagers revenant du sol lunaire et du CSM( Command Service Module) avec un homme à bord orbitant autour de la Lune et attendant ses camarades, avant le retour définitif à trois vers la terre.
Tout ceci pour dire que la technique du rendez-vous dans l'espace demande un traitement spécial. Une première partie traite des équations les mieux adaptées au problème et la suivante aborde quelques aspects concrets du rendez-vous spatial en orbite.
NB : Vous trouverez une présentation complète, précise, concrète, du rendez-vous spatial dans l'ouvrage du CNES
:MECANIQUE SPATIALE
TOME II
Chapitre 16
LE RENDEZ-VOUS SPATIAL
de
J LEGENNE
Je conseille vivement à tout étudiant, intéressé par la question, de se reporter à cette étude, notamment pour ceux qui abordent un projet concret de rendez-vous en orbite. L'auteur y a puisé, l'essentiel, de ce qu'il faut considérer comme un "digest" de base.
I EQUATIONS DE CLOHESSY-WHILTSHIRE :
1°) PRESENTATION ET DEFINITIONS :
Nous abordons le problème d'approche d'une cible S, généralement sur une orbite circulaire (C) et d'un chasseur M sur une trajectoire de manœuvre guidée alternant des phases propulsées et des périodes de vol balistique. Le guidage prend en compte vecteur position relative et la vitesse relative chasseur-cible. C'est donc un problème de mouvement relatif.
L'étude appréhende donc des variables locales et nécessite des notions locales.
Nous nous limitons au cas habituel d'une cible supposée en mouvement circulaire képlérien, ce qui signifie une orbite fixe en axes inertiels et une vitesse angulaire orbitale w constante.
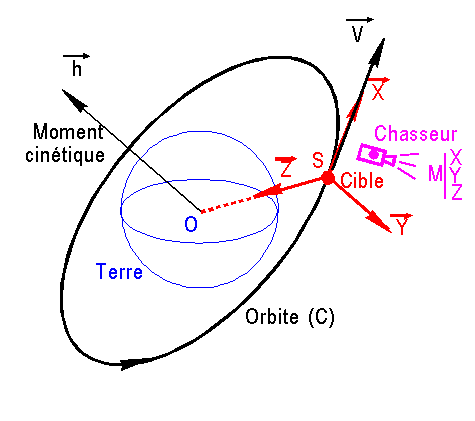
Classiquement, le repère orbital relatif noté R est associé à la cible S et aux directions privilégiées que sont: X l'unitaire de la vitesse orbitale et Z l'unitaire de la verticale descendante. Y l'unitaire qui complète le trièdre en direction opposée au moment cinétique orbital.
Le chasseur M se repère donc par rapport au repère orbital R de la cible par ses coordonnées cartésiennes relatives X, Y, Z.
b) Notations :
L'étude du mouvement relatif nous amène à introduire des notions relatives qui rappelleront au lecteur ses études scientifiques en mécanique des classes préparatoires ou de DEUG, relativement à la composition des mouvements.
Nous notons donc, pour le chasseur ou la cible:
|
r |
Le rayon vecteur scalaire de la cible |
|
|
Le rayon vecteur du chasseur dans le repère local |
|
|
Le rayon vecteur de la cible, en repère inertiel |
|
|
Le vecteur rotation du repère local R par rapport au repère inertiel. |
|
|
Le champ de gravitation en S, la cible |
|
|
Le champ de gravitation en M, le chasseur |
|
|
L'accélération inertielle due à toutes les forces autres que la gravitation newtonienne y compris les perturbations |
|
|
La vitesse relative du chasseur dans le repère local |
|
|
L'accélération de Coriolis du chasseur |
|
|
L'accélération d'entraînement du chasseur |
2°) EQUATIONS DE CLOHESSY-WHILTSHIRE :
Elles résultent simplement de la loi fondamentale de la dynamique appliquée à M, par rapport au repère relatif R, en projection sur les axes de R.
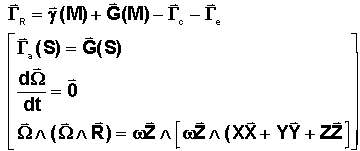
Le calcul fait apparaître la quantité G(M)-G(S) qui est le gradient du champ de pesanteur newtonien. Ce calcul étant important, nous le précisons un peu plus que les autres.
a) Gradient du champ de gravitation :
Il apparaît une matrice gradient du champ, prise en S.
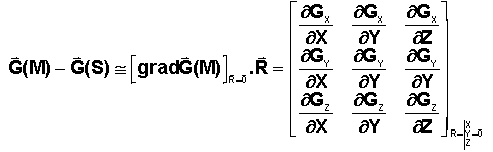
Le lecteur fera les calculs de dérivation de la fonction G(M) donnée plus haut pour obtenir :
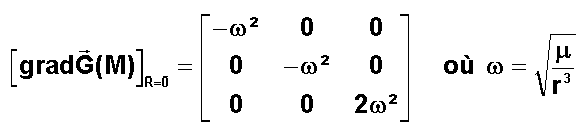
Le lecteur qui aura développé tous les calculs obtient les
EQUATIONS DE CLOHESSY-WHILTSHIRENB : Ces équations du mouvement, naturellement valables pour des valeurs de X, Y, Z petites devant le rayon orbital, montrent clairement le couplage X-Z et le découplage sur l'axe Y.
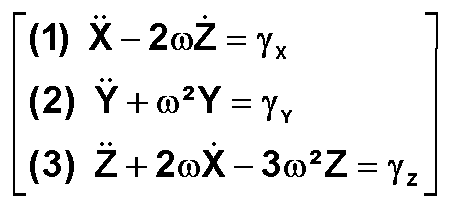
c) Conditions initiales :
En ce qui concerne la position, rien de particulier, il suffit d'évaluer Xo, Yo, Zo.
Le problème concerne l'évaluation de la VITESSE RELATIVE du chasseur DANS LE REPERE ORBITAL LOCAL L'ERREUR CLASSIQUE est de dire que la vitesse relative est la différence des 2 vitesses absolues. Or il s'agit d'une vitesse "vue" par un observateur lié au repère relatif. Donc le calcul relève de la composition des vitesses.
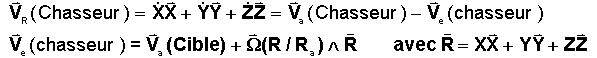
Exemple( qui sera repris plus loin)
:Le chasseur est sur une orbite circulaire, coplanaire à la cible, très voisine de la cible, dans la phase finale de l'approche. Le chasseur est donc légèrement en dessous et en arrière de la cible. Un transfert de type Hohmann est réalisé avec notamment une impulsion initiale DV dans le sens de X, et une impulsion finale pour " caler" derrière la cible. Intéressons nous au point de manœuvre au départ.
Le calcul demande d'évaluer, pour Z petit |
|
Il donne :
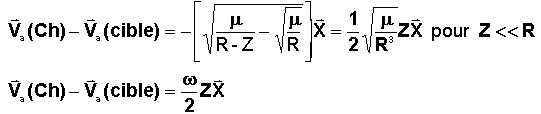
En final, on obtient les conditions initiales sur la vitesse :
![]()
II EXEMPLE D'APPLICATION DES EQUATIONS DE CLOHESSY-WHILTSHIRE :
Abordons par exemple la manœuvre classique en SCAO qui consiste à corriger périodiquement l'inclinaison orbitale, d'une quantité
Di petite, lors du survol d'un nœud. Nous savons que ces corrections coûtent cher et demandent l'utilisation de moteurs gaz chauds, sur des temps non négligeables. Il y a donc étalement de la manœuvre le long de l'orbite, sur une durée T. Quelle en est la conséquence sur le DV?La variation d'inclinaison étant faible, nous pouvons considérer que la cible est la position fictive d'un satellite sur l'orbite à corriger et que le "chasseur" est le satellite en phase propulsée avec une accélération
g et une poussée normale à l'orbite cible.Le calcul relève de l'équation (2) ci-dessus, où
g est l'accélération "hors plan orbital" de t=0 à t = T.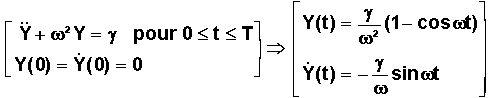
Pout t >T le système ci-dessous prend comme valeurs initiales, les valeurs finales de la phase propulsée précédente.
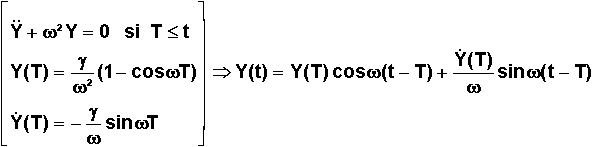
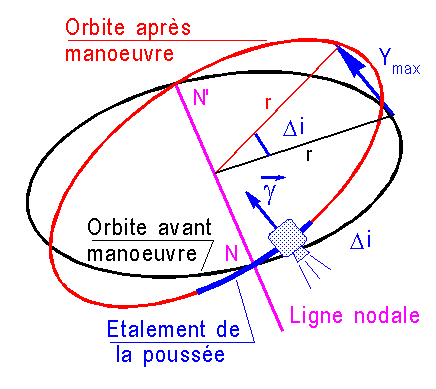
Il est clair que l'écart d'inclinaison est atteint quand l'écart hors plan Y est maximal. Cette valeur maximale vaut :
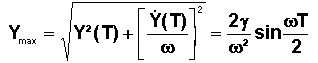
La correction d'inclinaison vaut alors :
![]()
Or classiquement la correction minimale vaut : |
|
Nous obtenons ainsi le rendement d'une poussée "hors plan", étalée sur un temps T :
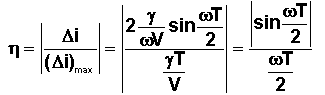
NB : Cette relation peut être rapprochée du
rendement d'une poussée donnée par un moteur fusée, en "spin".
![]()
Guiziou Robert septembre 2000
Il existe une version de mise en page
Optimisée pour Word 97:
R_V_SPAT.DOC