Suite du cours

EQUATIONS DE CLOHESSY-WHILTSHIRE ET

RENDEZ-VOUS SPATIAL

III LE RENDEZ-VOUS EN ORBITE:

Il n'est pas possible d'aborder ici tous les détails d'une telle mission, mais simplement d'aborder les questions essentielles, laissant le soin, au lecteur initié ou passionné d'en appréhender les finesses, dans la référence donnée plus haut.

1°) PROBLEMES POSES :

a) MEME PLAN D'ORBITE :

Si (P) désigne le plan orbital de la cible, il est impératif que le chasseur évolue dans ce plan pour rejoindre la cible. En effet, nous savons que les manœuvres consistant à changer de plan coûtent toujours très cher.

Exemple: un changement de plan de 1° pour une orbite circulaire à 200 km, coûte 136 m/s.

SOLUTION : le décollage de la base de lancement doit avoir lieu exactement à l'INSTANT DU PASSAGE DE LA BASE DANT LE PLAN ORBITAL (P). En pratique, c'est un peu plus complexe car le tir, pour des raisons de sécurité ou autres n'est pas strictement plan. Le but à atteindre est qu'à l'injection les plans orbitaux cible et chasseur soient confondus.

CONTRAINTE 1 : L'heure du tir est donc fixée par cette condition. On peut remarquer qu'il se présente deux opportunités par jour. Pour Kourou, en pratique, seuls les tirs vers le nord-est sont acceptables.

b) REPORT DE TIR :

On pourrait penser que l'heure du tir se conserve tous les jours, c'est oublier que la perturbation due à l'aplatissement polaire ( terme en J2 ) fait dériver l'orbite cible autour de l'axe nord-sud.

Il s'ensuit donc un décalage journalier de l'heure de tir possible de l'ordre de 30 à 33 mn/jour pour une cible en orbite circulaire entre 300 et 500 km, d'inclinaison voisine de 30°.

CONTRAINTE 2 : Variation de l'heure de tir pour 2 jours consécutifs, lors d'un report de tir.

c) PHASAGE CHASSEUR-CIBLE :

Au moment de l'injection sur Co, le chasseur et la cible sont dans des positions bien définies par la date et l'heure de tir. L'angle au centre de la terre, entre l'unitaire chasseur et l'unitaire cible, mesuré dans le sens du mouvement, s'appelle LE PHASAGE INITIAL DF.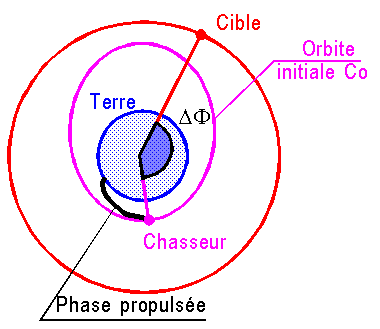

Comme d'un jour sur l'autre la cible n'effectue pas sauf hasard particulier, un nombre entiers de révolutions, cet angle DF peut donc varier de manière considérable, d'un jour à l'autre. Par exemple, la variation de DF peut atteindre 180° pour une orbite de type Navette gravitant vers 330 km du sol.

CONTRAINTE 3 : Cette variation du phasage en fonction du jour du tir, impose de mettre en place une stratégie de rendez-vous acceptant tous les phasages.

d) HORAIRES DE TRAVAIL :

Le rendez-vous étant une opération importante et complexe, les équipages chasseur ou cible doivent s'y préparer notamment sur le plan physique et en concentration. Donc bien avant le rendez-vous, les horaires de travail sont prédéfinis en fonction du rendez-vous, surtout qu'en orbite basse la notion de jour et de nuit perd son sens.

Classiquement, la montre des équipage est réglée sur 16 h, au moment de l'injection du chasseur sur Co.

A partir de là, la journée de travail devient classique, organisée en cycle de 24 h, comme à terre, avec un repos obligatoire de 20 h le soir jusqu'à 8 h du matin. Les manœuvres ne peuvent intervenir que durant les créneaux autorisés de travail.

CONTRAINTE 4 : Respect des horaires, ce oblige à des corrections de trajectoires dans des plages imposées.

e) DUREE DU RENDEZ-VOUS :

Le respect des horaires et une durée raisonnable de la mission, conduisent à envisager un rendez-vous exceptionnellement en 24 h et plus classiquement en 48 h, jamais plus.

CONTRAINTE 5 : La durée de l'ensemble des manœuvres est fixée à 48 h, entre l'injection sur l'orbite initiale Co et l'arrimage final.

2°) L'ORBITE C1 DE LA CIBLE :

Le rendez-vous concerne en général une station spatiale, à bord de laquelle des expériences scientifiques sont réalisées, notamment avec une microgravité qu'il vaut mieux avoir constante. Une ORBITE CIRCULAIRE est donc la norme.

L'altitude de la station va dimensionner les réserves d'ergols. Une altitude élevée demandera beaucoup de carburant et une orbite basse posera plutôt un problème pour les phasages élevés qui pourraient utiliser des orbites de dérives basses, entraînant des pertes conséquentes de vitesse par frottement atmosphérique. Il faut alors prendre en compte un surcoût en carburant.

Nous noterons R* le rayon de l'orbite cible, n* le moyen mouvement T* sa période.

2°) L'ORBITE Co DU CHASSEUR :

Généralement, le chasseur est injectée sur une orbite basse , circulaire ou elliptique, à périgée bas. Les performances lanceur assurent alors une masse maximale sur l'orbite initiale Co. Un inconvénient de périgée bas est l'usure de l'orbite par le frottement atmosphérique, surtout sensible au périgée.

Nous noterons Zpo et Zao les altitudes du périgée et de l'apogée de Co. Généralement Zpo > 150 km.

3°) LES MANOEUVRES :

De nombreuses stratégies sont possibles, chacune demandant une optimisation de la mission globale. Nous n'allons pas en dresser un bilan exhaustif, nous contentant d'un exemple et renvoyant le lecteur vers les articles spécialisés.

a) PROBLEME ESSENTIEL:

Il réside dans le phasage DF qu'il faut annuler en 48 heures. Pour ce faire, on laisse dériver le satellite sur des orbites intermédiaires, jusqu'à arriver à un déphasage nul au moment de l'approche finale. La cible et le chasseur sont alors sur la même orbite, à la même vitesse mais avec un écart minime en distance.

Les changements successifs d'orbite nécessite des allumages moteur qui doivent "tomber" dans les créneaux de travail équipages.

b) UN EXEMPLE DE STRATEGIE :

1- Injection à t = to ( 16 h équipages) au périgée sur Co.

2- Dérive sur Co durant No+0.5 orbites, soit un temps Dto.

3- Manœuvre à l'apogée de Co pour rejoindre, par une orbite elliptique C₁, durant un temps Dt₁, une ORBITE DE DERIVE CIRCULAIRE C de rayon R à déterminer. Premier incrément DV1 à l'apogée de Co et deuxième incrément DV2 à l' apogée de C₁ pour circulariser l'orbite

4- Dérive sur l'orbite C à déterminer, durant un temps Dt, jusqu'en M.

5- Allumage moteur en M pour rejoindre la cible en Q, par une orbite elliptique C₂, durant un temps Dt₂. Troisième incrément DV3, puis quatrième DV4 pour se stabiliser près de la cible.

NB :les moyens mouvements sont nommés n_o, n₁, n, n₂ et les périodes associées T_o, T₁, T, T₂

Coût = DV = DV1+ DV2+ DV3+ DV4

Inconnues du problème : No, R, Dt.

4°) LES EQUATIONS A RESOUDRE :

Traduisant que le phasage est annulé intégralement, le lecteur vérifiera que :

Une deuxième équation est fournie par la durée imposée de l'ensemble des manœuvres ( par exemple 48 h)

SYSTEME A RESOUDRE :

Naturellement, il faudra satisfaire en plus, aux contraintes d'horaire et optimiser le coût en DV.

NB : La méthode de formation des équations peut être généralisée à des orbites de dérive elliptiques, et à des manœuvres débutant au périgée ou à l'apogée de Co.

5°) Diagramme d'interprétation :

Une manière visuelle de présenter les manœuvres consiste à utiliser un diagramme d'évolution écart périgée-écart apogée comme ci-dessous:

On pose :

NB : Pour obtenir le détail complet des procédures, allez consulter l'ouvrage du CNES cité plus haut.

IV L'APPROCHE :

1°) LOCALISATION EN REPERE LOCAL :

A la fin du phasage, le chasseur se trouve sur une orbite (C**) circulaire de dérive, très voisine à quelques km près, de l'orbite circulaire de la cible Il s'agit alors de rejoindre la cible "en douceur".

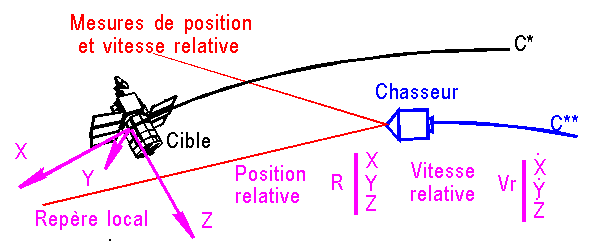
En pratique le chasseur se présente par " EN DESSOUS" et EN ARRIERE" de la cible. Il effectue alors des mesures de position et de vitesse relative, avant de décider de la stratégie à adopter.

Ainsi sont connues les conditions initiales

Les stratégies sont nombreuses et il n'est pas question de traiter tous les cas et nous nous limitons au plus simple.

On distingue en général 3 étapes essentielles :

L'APPROCHE INITIALE

L'APPROCHE FINALE

LA TRANSLATION FINALE

2°) Résolution des équations d'approche :

C'est l'occasion d'utiliser les équations de CLOHESSY-WHILSHIRE pour mettre au point la manœuvre. Seles les équations en X et Z nous intéressent : Les conditions initiales ont déjà été établies plus haut en I 2°) c)

L'élimination de X entre les 2 équations donne facilement la solution générale, dépendant de 5 constantes à déterminer ( une supplémentaire a été introduite à cause de la dérivation de l'équation en Z, lors de l'élimination de X ):

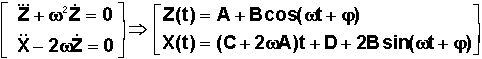
Les conditions initiales

Donnent ( Calculs que le lecteur fera ):

Le lecteur reconnaîtra l'équation générale d'une cycloïde, dont la forme dépend de DV.

3°) APPROCHE INITIALE ( HOMING ) :

But : passer de l'orbite de dérive circulaire C** de fin de phasage, sur une orbite d'attente stable, c'est à dire soit :

CAS 1 :Un POINT D'ATTENTE fixe par rapport à la cible, sur C*.

CAS 2: Une ELLIPSE D'ATTENTE à position moyenne nulle par rapport à la cible.

Dans tous les cas, le chasseur se situe sensiblement à un kilomètre environ derrière la cible.

A) CAS 1 PAR TRANSFERT EN 2 POUSSEES :

On suppose Yo = 0 . Typiquement la manœuvre est transfert de type Hohmann avec une poussée au périgée et une poussée à l'apogée.

a) Exploitation de la résolution pour la manœuvre qui nous intéresse :

Notre manœuvre consistait à rejoindre un point fixe derrière la cible, sur la même orbite que celle-ci. Il est clair que la durée est celle du transfert d'Hohmann soit une demi période de la cible, et donc w(t-to)=p, avec Z(t)=0.

On trouve

Donc pour "stopper" le chasseur derrière la cible, il faut encore donner une impulsion positive DV1=DV2. Le coût global de l'opération est donc DV = 2 DV1 = wZo/2.

AN : Pour une cible à 380 km du sol et Zo = 10 km, DV = 5.68 m/s

NB : Tout se passe comme si le chasseur "remontait" vers le point d'attente avec une pente a = 23°.

b) Allure des trajectoires d'approche :

NB : une étude complète de tous les cas est donnée pages 1116-1118 de l'ouvrage cité en tête de cet article. Le lecteur y trouvera aussi un formalisme complet de résolution des équations de CHLOHESSY-WHILTSHIRE. Nous ne donnons que les diverses formes, sans entrer dans les détails.

B) CAS 2 PAR TRANSFERT EN UNE POUSSEE :

On peut atteindre une ellipse stable derrière la cible avec un point chasseur moyen fixe en repère local.

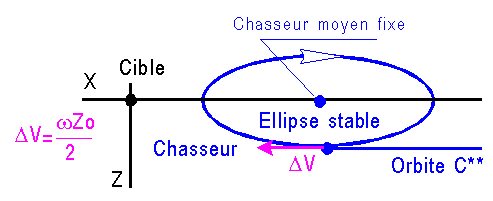
C) TRANSFERT EN POUSSEE CONTINUE :

On peut arriver au mêmes résultats, en terme de forme de trajectoires par une poussée continue sur une demi période. Le lecteur consultera les détails dans la référence déjà citée.

Par exemple pour le cas 1 le coût en DV est le même.

3°) APPROCHE FINALE ( CLOSING ) :

But : le chasseur vient se positionner derrière la cible à une centaine de mètres de celle-ci. Tous les types de propulsion sont possibles. Donnons juste un exemple, le lecteur effectuera les calculs, si nécessaire.

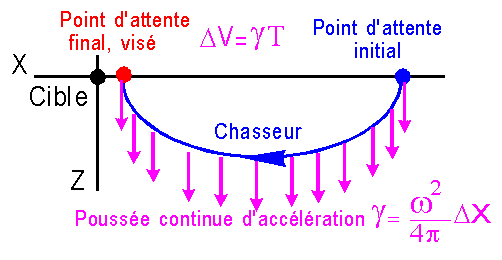
NB 1: Les équations de CHLOHESSY-WHILSHIRE doivent être intégrées en tenant compte, dans le cas d'une poussée continue, de la présence d'un second membre constant.

NB 1: Parvenu au point d'attente fixe, le chasseur effectue un retournement de 180°, pour présenter le mécanisme d'amarrage face à celui de la cible. Les ultimes mesures de position et de vitesse dont réalisées.

3°) TRANSLATION FINALE ( DOCKING ):

Il ne reste plus quelques dizaines de mètres à parcourir.

But : le chasseur se déplace suivant l'axe X, pour rester axer sur le centre du cône d'amarrage, dans lequel il viendra exercer une petite percussion en final. Rappelez -vous l'accident survenu à MIR lors d'un arrimage un peu sportif.

Là encore les équations de CHLOHESSY-WHILTSHIRE viennent à notre secours pour constater les conséquences de la translation suivant Z.

Le plus souvent le choix se porte vers une vitesse continue, constante sur X, créée par une impulsion initiale. Pour "contrer" le déplacement suivant Z, une compensation est effectuée en actionnant un actuateur donnant une accélération constante suivant l'axe Z, de niveau lié à la vitesse sur X, comme le montre la formule. Naturellement, une impulsion finale de même niveau que l'initiale est nécessaire pour s'arrêter très près de la cible.

Pour conclure :

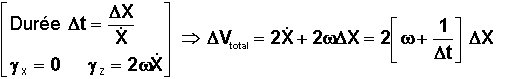
On note que pour une distance donnée, le coût en DV diminue si on augmente la durée de l'approche finale.

NB 1 : Position et vitesse sont naturellement mesurées en continu, par un senseur de rendez-vous.

NB 2 : Vous trouverez une remarquable simulation, réalisée avec les données de la navette HERMES, qui malheureusement n'a jamais volé, chapitre 28 , page 1811-1847, de l'ouvrage cité en référence.

Guiziou Robert septembre 2000

Il existe une version optimisée pour la mise en page

Sous Word 97 : R_V_ORB.DOC