|
STABILISATION PAR SPIN |
![]()
|
CONTENU : Mis à jour en août 2000, revu sept 2011 I GENERALITES : Comportement gyroscopique - Raideur gyroscopique - Couple gyroscopique II
REPONSE
A UN COUPLE CONSTANT : Equations - Interprétation - Exemple pratique III DEPLACEMENT DU MOMENT CINETIQUE |
|
![]()
NB
: Le lecteur se reportera au cours sur le mouvement de Poinsot, pour revoir les définitions et conventions d'écriture utilisées dans
cette page.
Dans
tout ce qui suit, nous supposerons que la rotation axiale est contrôlée en
continu par un gyromètre de mesure et un actionneur, par exemple une paire de tuyères
fournissant un couple de commande Cm sur l'axe de roulis.
1°)
PRINCIPE MECANIQUE :
La
stabilisation par "SPIN" ou encore "Raideur gyroscopique",
repose sur le résultat capital du mouvement de Poinsot, qui indique que si la
rotation du solide est portée par un axe principal d'inertie, cet axe restera
fixe dans l'espace inertiel. Nous avons aussi montré que le mouvement libre est
stable si cet axe est celui de plus grande inertie, notamment en présence de
dissipations internes.
L'étude
a également montré qu'en cas d'imperfections du mouvement, l'angle de nutation
est d'autant plus petit que la rotation axiale est grande.
QUESTION :
Que se passe-t-il en présence de couples externes ? Un rappel de mécanique en
2°), concernant le couple gyroscopique est nécessaire.
2°) COMPORTEMENT GYROSCOPIQUE
:
Nous
dirons qu'un corps a un comportement gyroscopique lorsque sa rotation axiale
est très grande devant sa rotation transversale. C'est le cas des satellites
stabilisés par spin, puisque la stabilisation est destiné à maintenir les
rotations transverses nulles ou très petites.
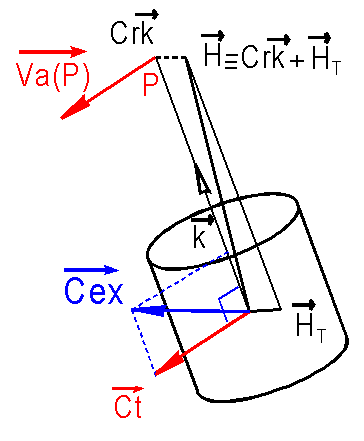
Le
moment cinétique H se décompose en une composante axiale Cr très grande devant
l'autre composante transverse HT.
On
dit qu'on utilise l'APPROXIMATION GYROSCOPIQUE lorsqu'on néglige la composante
transversale de H devant sa composante axiale Cr .
De
même le moment ou couple des efforts extérieurs appliqués au satellite possède
une composante axiale et une composante transversale. Cette dernière est
annulée par la commande des tuyères en roulis.
On
supposera donc que l'on confond le moment cinétique avec sa composante axiale
et on appelle P l'extrémité du moment cinétique approché. Le mouvement de P a
l'avantage de nous renseigner fidèlement sur le mouvement de l'axe satellite et
donc du dépointage ou de la nutation.
Le
théorème du moment cinétique appliqué en repère inertiel donne :
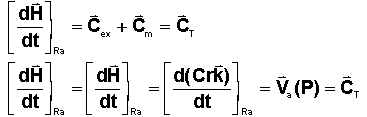
Ceci
nous donne un premier résultat fondamental en gyroscopie :
LA VITESSE Va(P) DE L'EXTREMITE P DU MOMENT CINETIQUE EST EGALE
AU MOMENT TRANSVERSE DES EFFORTS EXTERIEURS APPLIQUES AU VEHICULE

NB : Ne soyez pas
étonné de l'apparente différence dimensionnelle de la vitesse et du moment
donnés pour égaux. En effet la longueur OP qui a été dérivée a pour dimension
celle d'un moment cinétique.
PARADOXE GYROSCOPIQUE :
Normalement
le bon sens mécanique habituel indique qu'un couple appliqué à un solide a
tendance à créer une rotation dont l'axe est proche de celui du couple
appliqué.
Ici,
on constate que la vitesse de P est parallèle au couple, ce qui constitue un
paradoxe et conduit à la règle suivante :
L'axe
d'un gyroscope a tendance a s'aligner sur le couple appliqué et par conséquence
sur la rotation qu'on veut lui appliquer.
C'est
cette propriété qui empêche une toupie de "tomber" et lui fait
prendre un mouvement conique.
Appelons
w la mesure de la vitesse angulaire
transversale qui est engendré par le couple.
Cette
vitesse porte le nom de précession du gyroscope, c'est elle qui engendre la
nutation.
Couple
--> Vitesse de P --> rotation transverse
Le
lecteur vérifiera sans peine qu'exprimée en norme :
Va(P)
= w*OP = w * H = w*Cr
Ainsi
:
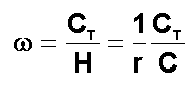
Montrant
que w est d'autant plus petite que la
rotation r est grande. Cet effet du spin s'appelle la "RAIDEUR
GYROSCOPIQUE", c'est elle qui associée à un fort moment d'inertie donne au
gyroscope des réactions aussi lentes et d'amplitude réduites lors d'une
perturbation transverse.
La
RAIDEUR GYROSCOPIQUE est aussi la propriété
Explicitons
l'application du théorème du moment cinétique sous l'hypothèse d'une nutation
très faible :

Comme
la rotation r sous asservissement est maintenue constante, on en déduit :
![]()
Nous
avons introduit un couple Cg appelé couple gyroscopique. Il n'existe que si la
rotation du véhicule n'est pas portée par l'axe de spin.
REMARQUE :
Ce
couple gyroscopique apparaît comme une réaction du gyroscope à s'opposer à
toute rotation qui dérangerait son équilibre et son pointage stable.
De
même ce couple gyroscopique s'oppose à l'action des couples extérieurs qui ont
tendance à vouloir le faire tourner.
C'est
ce phénomène qui explique les comportements spéciaux des corps tournants.
Ce
paragraphe pourrait être considéré comme un exercice de mécanique générale.
Nous supposons que le satellite est de révolution inertielle ( A = B )autour de
l'axe k où l'inertie est C.
La
suite s'intéresse à l'évolution de la rotation transversale w.
1°)
PROBLEME :
Le
contrôle d'un satellite est réalisé par un système de tuyères en nombre pair,
fonctionnant en tout ou rien, délivrant un COUPLE CONSTANT EN AXES SATELLITE
noté :
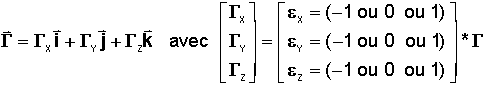
La
disposition des tuyères permet de contrôler chaque axe séparément.
L'axe
de roulis est celui du spin.
Il
est clair que durant le fonctionnement du contrôle actif par tuyères, le niveau
des couples est très grands devant celui des perturbations qui seront donc
négligées.
Le
lecteur établira en adaptant les calculs du mouvement de Poinsot :
Pour
la suite nous supposons la vitesse de spin r stabilisée et donc le couple GX nul.
On
pose une variable complexe Z = p+iq intimement liée au mouvement
Z
est l'affixe de la rotation transversale w, dans
les axes i et j.

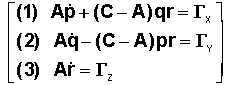
L'équation
(3) confirme r = W = Cste
La
combinaison de (1) et (2) donne après mise en forme de l'équation, une forme
agréable pour son exploitation :
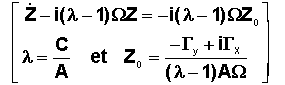
2°)
INTEGRATION ET SOLUTION :
L'intégration
de l'équation donne avec l'utilisation des constantes l, W* et Z0 :
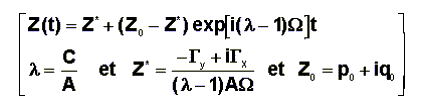
3°) INTERPRETATION DU MOUVEMENT
:
Nous
touchons au cœur du problème de la commande par tuyères et du contrôle de la
nutation.
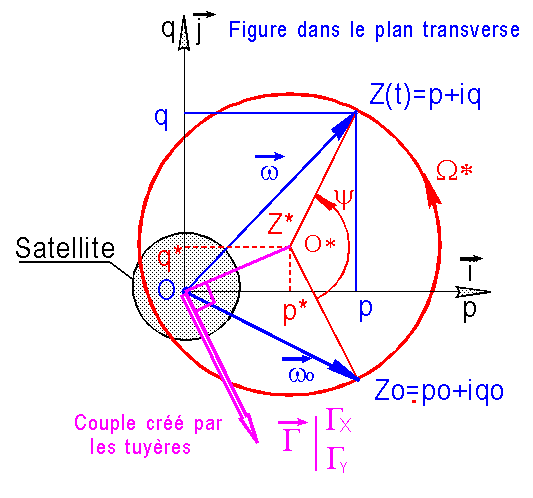
Il
faut bien comprendre que le complexe Z(t) représente
dans les axes i et j ( ou pet q ) liés au satellite les composantes de la
rotation transversale w, celle même qui est responsable de la nutation parasite du
satellite.
Le
résultat de 2°) montre clairement que pendant
l'application du couple de commande, dans le plan transverse du satellite et vu
du satellite, le vecteur w décrit un cercle de centre O* d'affixe Z* et de rayon R* =
|Z0 - Z*|, à une vitesse angulaire constante W*, autour de l'axe de spin k. Le sens de ce mouvement dépend de
la valeur de l'allongement inertiel l
par rapport à 1, en général l > 1.
Un
CONTROLE DE LA NUTATION équivaut à ANNULER Z(t).
NB
1 : Tout changement dans la commande se
traduit par un décalage du centre de nutation et donc du rayon du cercle. Même
si c'est difficile à imaginer il faut faire l'effort de réfléchir à cette
question, qui est à la base de toute stratégie de commande d'un engin spatial.
Le
centre du cercle décrit par w a pour
coordonnées Z*=p* + iq* avec
![]()
|
Le
rayon du cercle vaut : |
|
NB2
: Comme les moteurs fonctionnent en tout ou rien et en parallèle ou pas, il y a
8 possibilités de commande. En pratique une bonne stratégie consiste à
n'utiliser qu'un seul couple de tuyères à la fois.
NB 2 : Le lecteur n'oubliera pas que le mouvement de
nutation est créé par w et que la rotation induite s'opère autour du moment
cinétique H. Or toute application d'un couple transverse déplace le moment
cinétique en axes inertiels. Il faut donc combiner ces 2 mouvements, pour
obtenir la trajectoire absolue du moment cinétique.
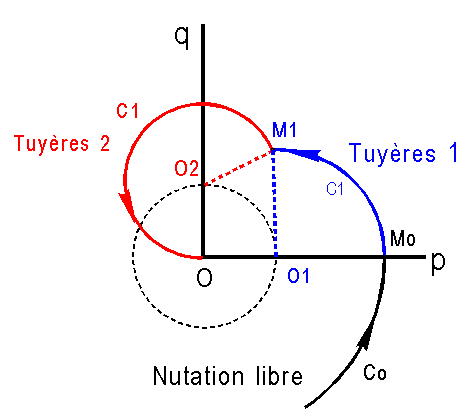
3°) EXEMPLE THEORIQUE DE CONTROLE
:
L'exemple
est purement mathématique, mais pourrait fort bien être utilisé en pratique,
pour annuler une nutation. M est l'extrémité de w.
On
appelle G la norme du couple créé par 2 tuyères opposées. On introduit les
points O1, O2, O3, O4 centres de
cercles possibles à décrire suivant les tuyères mises en jeu.
![]()
1-
Au départ le satellite est en nutation, style Poinsot (cercle Co)
2
- Au temps to, un capteur détecte en Mo, qo = 0, et alerte les tuyères agissant
sur l'axe j, avec un couple G1 = - G j.
Le
cercle décrit par M est alors C1, de centre O1.
3
- Au temps t1, le point M est M1 tel que O2M1=
O2O = R. Les tuyères précédentes sont stoppées et sont alertées celles
donnant un couple G i.
Le
point M décrit alors le cercle C2 qui ramène la nutation à 0. Deux opérations
ont suffit.
La
figure suivante illustre la logique du contrôle en nutation :
NB
: Il restera encore à contrôler que l'axe de spin est bien pointé et donc
éventuellement à déplacer l'axe de spin sans créer de nutation parasite.
4°) EXEMPLE PRATIQUE DE CONTRÔLE
:
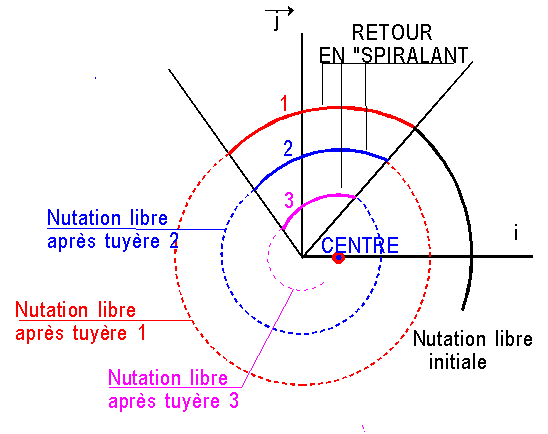
On
peut aussi travailler en impulsions de courte durée, par exemple sur une
détection q = 0 et en appliquant un couple <0 porté par j. L' extrémité de w
va "spiraler" autour de l'origine et donc le module diminue. La
figure ci-dessous montre l'évolution.
III DEPLACEMENT DU MOMENT
CINETIQUE :
C'est
le second volet du contrôle d'attitude par spin. Le moment cinétique doit
posséder 2 propriétés :
1
- Etre porté par l'axe de spin, ce qui est réalisé lorsque la nutation est
annulée.
2
- Etre pointé dans la direction souhaitée. Lorsque cette condition n'est pas
satisfaite, le moment cinétique doit être déplacé.
Pour
simplifier l'écriture mais sans restreindre la généralité du calcul, nous
supposons que le couple G créé est porté par l'axe j.
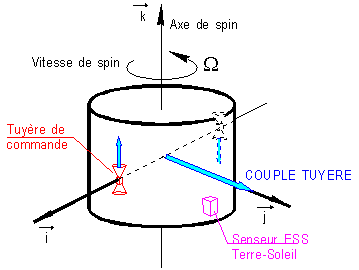
Il
faut bien comprendre que le satellite est spinné et donc que l'effet du couple
est modifié par le spin.
Le
point de départ est le théorème du moment cinétique appliqué en axes inertiels:

Le
signal de déclenchement des tuyères est donné d'après une référence soleil, de
manière à ce que la variation de H soit bien positionnée.
Calculons
l'effet de la manœuvre, en notant Dt
le temps d'allumage et DF la rotation de spin effectuée
durant Dt.
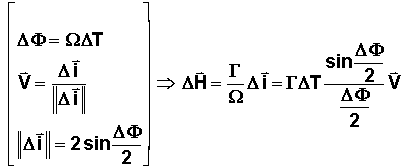
|
|
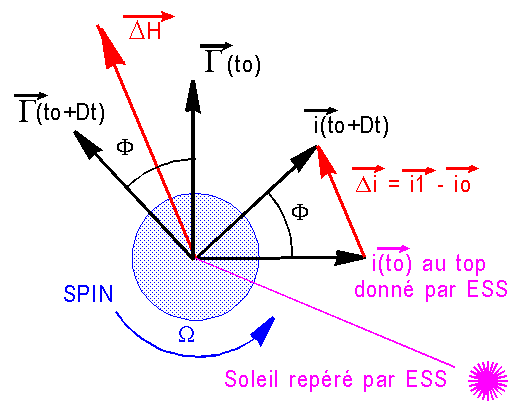
Nous
abordons ici, l'aspect pratique du contrôle d'attitude par spin. Par commodité
nous avons positionné 2 tuyères sur l'axe i, donnant un couple G sur l'axe j.
1°)
Repérage de l'axe de spin et mesure de la nutation:
Sous
l'effet des couples perturbateurs externes, l'axe de spin dérive et le moment
cinétique aussi.
L'axe
de spin précessionne autour du moment cinétique H qui n'est pas dans la bonne
direction.
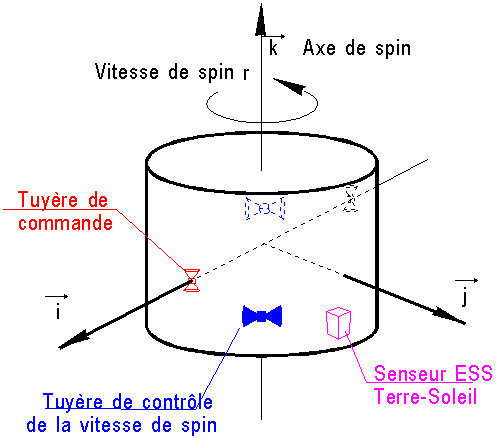
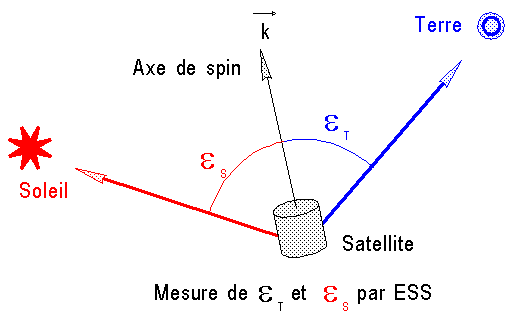
a) Mesure de la direction de
l'axe de spin k :
Un
senseur terre-soleil suffit pour reconstituer la direction de k, connaissant
celle de satellite-terre et satellite-soleil.
b)
Contrôle de la vitesse de spin r:
Soit
par un gyromètre sensible sur l'axe k, soit le senseur ESS en mesurant la
période de défilement du soleil ou de la terre. La correction est effectuée par
2 tuyères donnant un couple suivant l'axe de spin k, donc sans en modifier le
pointage.
2°)
Déplacement de l'axe de spin :
Il
s'agit alors de réaliser 2 opérations :
a)
- Réorientation du moment cinétique H : pour cela on ouvre une
tuyère déclenchée sur un "top" à un instant T après un
"top" de référence de passage soleil, par ESS. On ouvre cette tuyère
durant un temps DT de manière à ce que le vecteur DH soit correct, quitte à recommencer plusieurs fois
l'opération.
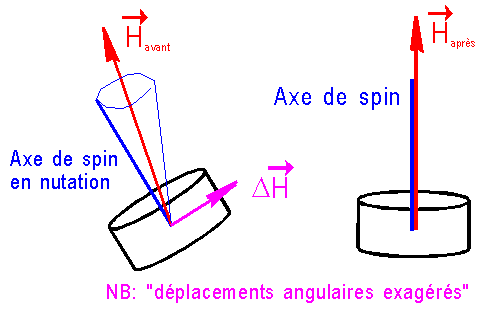
NB
: Le déplacement du moment cinétique, sauf hasard heureux où l'axe de spin
"tombe pile" sur H, crée inévitablement un mouvement de précession.
b)-
METHODE POUR EVITER UNE NUTATION IMPORTANTE :
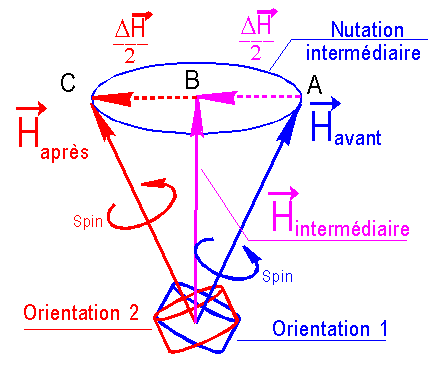
La
manœuvre de réorientation de H est"éclatée" en 2 parties, dans
lesquelles on délivre la moitié de la correction de H.
En
A au temps to, on délivre DH/2,
l'extrémité de H vient en B. Un mouvement de nutation s'amorce et l'extrémité
de H vient en C au bout sensiblement d'une demi période de nutation Tn.
Au
temps to+Tn/2, on délivre DH/2 à nouveau.
Très sensiblement l'axe de spin et le nouveau moment cinétique sont colinéaires
et la nutation résiduelle est faible.
c)
Amortir le mouvement de nutation qui commence
après
réorientation du moment cinétique : En effet le nouveau moment cinétique n'est
pas exactement sur l'axe k et donc s'amorce une nutation qu'il faudra réduire,
pour retrouver un pointage correct suivant H. De plus les perturbations sont là
pour amplifier ce mouvement.
Les
stratégies pour y parvenir sont nombreuses, voir plus haut.
Un
"Spinner" (satellite spinné) présente un inconvénient évident et
majeur qui est l'impossibilité de pointer une charge utile embarquée (
télécommunications, caméras, télescope...) et des avantages d'avoir une
régulation thermique plus simple( pas de face froide et de face chaude), ainsi
que la possibilité de disposer des cellules solaires sur la surface externe du
satellite.
Ce
problème a été résolu par un compromis, le satellite "DUAL-SPIN".
Il
est composé d'une partie spinnée(rotor), équipée de cellules solaires et d'une
plate-forme déspinnée(inertielle), porteuse des équipements nécessitant
notamment un pointage strict.

Profitons
de ce cours pour montrer sur un cas concret l'effet stabilisant du spin lors
d'une phase propulsée de lanceur,.à l'occasion d'une manœuvre importante
d'apogée ou d'évasion ....
1°)
PROBLEME :
1
- Le lanceur est orientée dans la bonne direction
2
- Il est mis en SPIN de vitesse angulaire W
autour de son axe longitudinal, principal d'inertie. Il peut subsister une
petite nutation parasite due aux erreurs de pointage...mais considérée comme
nulle
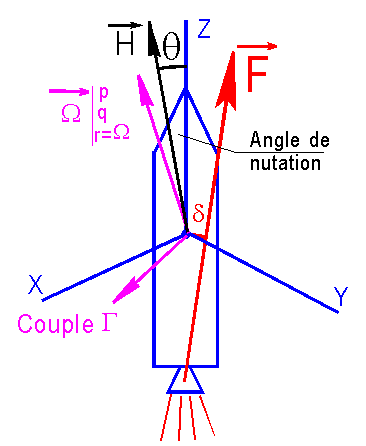
3
- Le moteur supposé à tuyère fixe(moteur à poudre) est allumé durant un temps
Tc. De toute évidence l'axe de la poussée ne peut passer par le centre
d'inertie et donc apparaît un couple dû à ce mésalignement. Nous le noterons en
module :G = F d, où F est la force, d la distance
du centre d'inertie G à l'axe de la force de poussée.
NB
: Il est clair que le défaut ne dépend que du lanceur et de son moteur, donc le
couple parasite transverse est constant en axes satellite et le calcul
relève de la théorie développée en II.
2°)
RESULTAT: MOUVEMENT DE ROTATION :
Rappelons
qu'avec Z = p + iq, Zo = po + iqo nous avons trouvé comme résultat général :
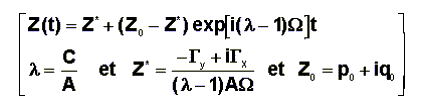
Nous
pouvons admettre qu'au moment de l'allumage la stabilisation du pointage est
achevée et que la rotation transversale est nulle ( Zo = 0 )
La
nutation est caractérisée essentiellement par la norme de la rotation
transversale( composantes p et q) donc par la norme du complexe Z, affixe de w.
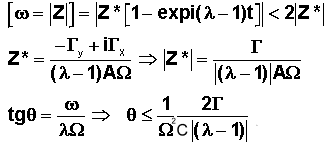
Le
calcul montre explicitement que la nutation est limitée et que son amplitude
est d'autant plus petite que la vitesse de spin est grande, surtout en
apparaissant au dénominateur avec son carré.
C'est
une vérification éclatante de la notion de RAIDEUR GYROSCOPIQUE.
L'effet
gyroscopique, en faisant tourner le couple avec le lanceur, moyenne les effets
du mésalignement de la poussée.
VI CONCLUSION :
En
résumé un contrôle d'attitude par SPIN est relativement simple et ne demande
qu'un nombre limité d'équipements:
![]() 3
tuyères : 1 pour déplacer l'axe de SPIN, 2 pour réguler la vitesse de spin
3
tuyères : 1 pour déplacer l'axe de SPIN, 2 pour réguler la vitesse de spin
![]() 2
senseurs: 1 senseur Terre et un senseur Soleil
2
senseurs: 1 senseur Terre et un senseur Soleil
![]() Si le
système est doté d'un contrôle de nutation passif, un senseur de nutation.
Si le
système est doté d'un contrôle de nutation passif, un senseur de nutation.
![]() Enfin
un amortisseur passif est éventuellement nécessaire.
Enfin
un amortisseur passif est éventuellement nécessaire.
![]()
Guiziou Robert 12 août 2000, sept
2011
