CONTENU : Mis à jour 18 janvier 1999Jupiter | Astéroïde IDA | Astéroïde Gaspra |JPL Historique de la mission | Géométrie du survol Sphère d'influence | Problème de Lambert Tremplin gravifique | Constante C3 |
|
|
RAPPELS DE COURS |
CONTENU : Mis à jour 18 janvier 1999Jupiter | Astéroïde IDA | Astéroïde Gaspra |JPL Historique de la mission | Géométrie du survol Sphère d'influence | Problème de Lambert Tremplin gravifique | Constante C3 |
|
![]()
Cinquième planète du système solaire, diamètre 142000 km, densité 1.36, avec une rotation sur elle-même en 9 h 50 mn.
C'est une énorme boule de gaz , essentiellement composée d'hydrogène et d'hélium. La haute atmosphère est ténue, à une température de 150 K , au dessous de celle-ci se trouve une zone de turbulences et de vents violents , la température y est de 370 K. Allant vers le centre, l' atmosphère s'épaissit à 90% d'hydrogéne, 9.8% d'hélium et une petite quantité de méthane ,acétylène, éthylène et benzène.
Plus bas règne une brume et des nuages blancs de cristaux d'ammoniac ou d'hydrocarbures à une température de 120 K .La pression est de l' ordre de 0,6 atmosphère.
Puis la pression augmentant régulièrement, on rencontre alors du CO, de la vapeur d'eau. En dessous au delà d'une pression de 40 atmosphères , c'est le domaine inconnu des hypothèses.
On pense qu'à des pressions énormes les gaz se liquéfient et que probablement vers 2 millions d'atmosphères il apparaît de l'hydrogène métallique à une température de 10000 K.
Au cœur, les spécialistes pensent qu'il existe un noyau solide de silicates, de métaux et de glace, très chaud et qui constitue la source d'énergie de la planète.
Pour obtenir des caractéristiques orbitales de Jupiter vous pouvez activer une application extérieure qui donne les éphémérides des planètes. Pour ce faire cliquer le bouton ci-dessous, qui lance un éxécutable
![]()
Paramètres intéressants pour nous, sont :
NB : Le moyen mouvement est la vitesse angulaire moyenne
Coordonnées dans le repère héliocentrique J2000 le 28/8/1993 à 0 h:
NB: 1 UA = 149.5968 106 km = distance Terre- soleil
![]()
Paramètre principaux :
NB : 1 UA = 149.5968 106 km
NB: Le moyen mouvement est la vitesse angulaire moyenne
Coordonnées en UA, dans le repère héliocentrique J2000, le 29/10/1991 à 0 h:
![]()
Le projet de lancement de la sonde Galiléo était prévu de longue date. En effet le vol initial était programmé sur la mission n° 29 de la navette US Atlantis le 21 mai 1986. L'engin devait être accouplé à un étage à hydrogène de la fusée Centaure, délivrant l'incrément de vitesse nécessaire pour la libération de l'attraction terrestre et permettre un voyage de 2 ans pour atteindre
jupiterHélas l'accident de Challenger est venu perturber le calendrier et remettre en question le projet, puisque le logement de tout réservoir à hydrogène dans la soute a été interdit.
Les ingénieurs du JPL de la NASA se sont mis au travail et grâce aux ressources de la mécanique céleste et notamment à l'utilisation de tremplins gravifiques, ont imaginé ce voyage exceptionnel de Galiléo.
![]()
![]()
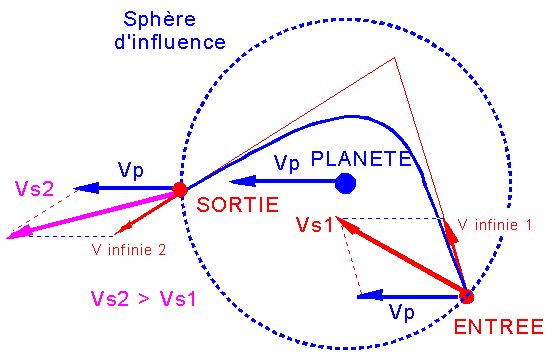
On rappelle qu'on désigne par tremplin gravitationnel ou Swing-by en anglais, la réaction de gravitation et d'entraînement qu' exerce une planète sur une sonde qui passe relativement près de celle-ci.
Voir la géométrie du survolOn appelle Vp la vitesse héliocentrique de la planète, Vs1 et Vs2 respectivement la vitesse héliocentrique de la sonde juste avant de pénétrer dans la sphère d'influence de la planète et juste après sa sortie de cette
zone d'influence.Vectoriellement on a les relations suivantes de changement de repère:
![]()
où Vs1 et Vs2 désignent les vitesses de la sonde, mesurées par rapport au repère héliocentrique, à l'infini de la planète
![]()
D
V désignant la norme du "cadeau" que fait la planète à la sonde. La planète joue le rôle d'entraînement comme dans un relais cycliste sur piste.Nous savons que si le survol au plus près de la planète a lieu à une distance minimale ( périgée ) rp du centre et que la vitesse infinie est connue alors
la norme de l'accroissement de vitesse est :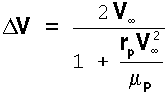
Périastre de l'hyperbole de descente
:La position du périastre est capitale de par sa précision pour bien "caler" l'orbite héliocentrique à la sortie de la sphère d'influence de la planète.
Actuellement le survol d'une planète peut être réalisé à mieux que le km près en altitude.
Dans des missions futures sur Mars il sera peut être envisagé de placer le périastre de l'hyperbole de descente dans l'atmosphère martienne afin de réaliser un freinage et une capture, à la manière des retours lunaires.
Vitesse à l'infini de sortie de la sphère d'influence
:
Cette vitesse égale en norme à la vitesse à l'infini d'arrivée ( conservation de l'énergie sur l'hyperbole ) est portée par la deuxième branche de l'hyperbole.
Pour obtenir une augmentation maximale de la vitesse, il faut essayer de placer cette vitesse colinéairement et de même sens que la vitesse de la planète. Il vaut mieux alors opérer un survol par derrière la planète.
Vitesse absolue d'arrivée
:C'est la vitesse Vs1 par rapport au soleil, qui se calcule sur l'orbite héliocentrique, en dehors de la sphère d'influence de la planète par conservation de l'énergie spécifique.
En général pour une orbite "montante" cette vitesse est plus petite que celle de la cible et pour une orbite "descendante" elle est plus grande que celle de la cible.
![]()
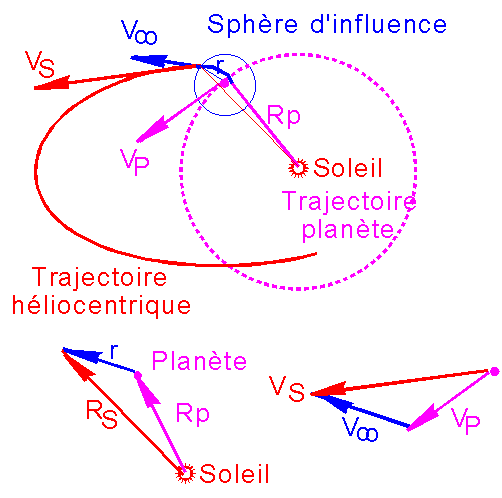
On rappelle que la sphère d'influence d'une planète est la zone entourant cette planète, dans laquelle l'attraction du Soleil peut être négligée avec une excellente approximation. Naturellement à l'extérieur, c'est l'attraction de la planète qui est négligée.
Pour la Terre le rayon de cette sphère d'influence est de l'ordre de 900000 km. Pour Jupiter elle avoisine 50 millions de km
De manière générale si D est la distance Soleil - Planète et
mp, ms, les constantes de gravitation du Soleil et de la planète le rayon de la sphère d'influence vaut :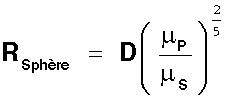
![]()
On appelle ainsi classiquement la quantité :
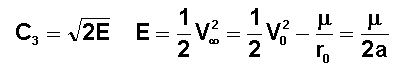
capitale pour le choix du lanceur et de la masse utile envoyée.
En effet c'est elle qui représente les capacités du lanceur sur l'orbite hyperbolique de départ, puisque c'est tout simplement le double de l'énergie mécanique à communiquer à la sonde; ( cinétique et potentielle ) sur l'orbite hyperbolique.
![]()
0
L'anomalie excentrique est un paramètre angulaire variant de 0 à 2p, permettant de localiser de manière unique la position d'un corps sur une orbite elliptique.
On s'attachera ci-dessous à bien faire la différence entre f et q.
On rappelle le paramétrage :
j
en radian, tp est un temps de passage au périgée
NB : Il faut faire attention lors de l'inversion des lignes trigonométriques, au bon choix de l'angle, car il y a toujours 2 valeurs possibles correspondant à 2 points symétriques par rapport au grand axe.
![]()
On appelle ainsi le problème qui consiste à déterminer la trajectoire elliptique unique, quand elle existe, qui relie deux points donnés de l'espace, en imposant les positions et le temps de parcours, c'est à dire l'écart entre les deux dates de départ et d'arrivée.
Naturellement on travaille dans l'hypothèse des
sphères d'influence dans le cas du départ ou de l'arrivée sur une planète. Un programme vous posera la question au moment opportun. Essayez ci-dessous.NB :Si la position initiale finale est un point précis, alors le programme demande les coordonnées de ce point dans le repère absolu.
En sortie vous obtiendrez: les éphémérides des planètes, leur vitesse, les caractéristiques de la trajectoire elliptique de Lambert, les vitesses de départ et d'arrivée ainsi que les vitesses à l'infini de départ et d'arrivée par rapport à la planète de départ et d'arrivée.
Essayez ce programme directement ici :
DEUX_PTS.EXE ![]()
Jet Propulsion Laboratory de la NASA. Organisme particulièrement chargé des voyages interplanétaires.
![]()
1°) REPERAGE DU PLAN ORBITAL :
Nous savons qu'avec une excellente approximation, le plan équatorial terrestre est fixe dans le repère inertiel IJK. Le plan orbital coupe le plan équatorial suivant une droite appelée
LIGNE DES NOEUDS.Ces 2 points sont importants dans les applications pratiques, parce que d'une part nous verrons que c'est le lieu des corrections d'inclinaison, mais également ils délimitent, pour les pays de l'hémisphère nord, la zone utilisable.
NB : Des définitions équivalentes pourront être données, des paramètres orbitaux ou des vecteurs fondamentaux, pour le repère héliocentrique écliptique ou tout autre repère planétocentrique. Ce n'est que par habitude que nous les fournissons dans IJK.
Longitude vernale W ou heure sidérale de la ligne des nœuds :On appelle
W l'angle, mesuré positivement autour de K, entre l'unitaire I et le vecteur nodal n. Conventionnellement, il est exprimé entre 0° et 360°.![]()
Cet angle conditionne naturellement le positionnement du plan orbital par rapport à l'espace inertiel environnant. Donc tout naturellement, comme le soleil est mobile dans cet espace,
W et le temps interviennent dans les problèmes d'éclairement des panneaux solaires et la gestion de l'énergie.Le calcul de
W est simple, si on lui adjoint une test à ne pas oublier.
On appelle inclinaison de l'orbite l'angle i, mesuré entre 0° et 180°positivement autour le l'axe n, entre le plan équatorial et le plan orbital. C'est encore l'angle entre les normales aux 2 plans, donc entre K et h (ou W).
Le calcul donne sans difficulté ;

Nous le verrons plus loin, mais à l'évidence plus l'inclinaison orbitale est forte, plus on peurt survoler des latitudes élevées.
Quelques valeurs classiques :
I=0° Orbite équatoriale, essentiellement l'orbite géostationnaire.
I=28° Inclinaison habituelle des orbites des vols Navette US
I=63°.4 Inclinaison orbitale fréquemment utilisée par les satellites soviétiques, car c'est une valeur qui leur permet de pallier une perturbation due à J2.
I=90° Orbites polaires pratiquées par les satellites météorologiques en orbite basse, leur permettant de suivre 15 fois par jour les masses d'air polaire.
I=98°.7 Inclinaison choisie par les satellites de la famille SPOT, gravitant vers 822 km du sol, travaillant en imagerie spatiale et utilisant grâce à une valeur bien choisie de i, la propriété
d'héliosynchronisme. Vu du nœud ascendant le satellite se déplace vers l'ouest, contrairement à 90% des satellites.I=5° Inclinaison ce l'orbite lunaire
I=23° 27' Inclinaison de l'orbite décrite par le soleil vu de la terre, avec passage au nœud ascendant au moment du printemps..
2°) REPERAGE DU GRAND AXE DANS SON PLAN :
On appelle
w ARGUMENT NODAL DU PERIGEE, l'angle orienté des vecteurs n et e mesuré positivement entre 0° et 360° autour de l'axe W.
3°) PARAMETRES DE FORME DE L'ORBITE :
On retient les paramètres classiques a et e, déjà rencontrés.

4°) PARAMETRE DE POSITION SUR L'ORBITE :
Le dernier des paramètres orbitaux, est en fait constitué de deux données, une position sur l'orbite et un temps correspondant à cette position. Les choix sont variables en fonction du problème traité.
L'anomalie moyenne Mo=
jo - esinjoCONCLUSIONS: |
|
Paramètres orbitaux : |
|
![]()
Vecteur moment cinétique h
Vecteur nodal n
Vecteur excentricité e
Ces trois vecteurs permettent le
calcul des paramètres orbitaux![]()
Guiziou Robert 18 janvier 1999