EXPLOITATION D'UNE SIMULATION COMPLÈTE

J'appelle ainsi les simulations qui prennent en charge le nanosatellite de l'injection jusqu'à la première acquisition fine à l'instant où les angles de roulis, lacet et tangage passent tous sous le seuil acceptable pour la mission. Ce seuil est un des paramètres à optimiser, car il conditionne la durée de l'acquisition primitive..

Elles reposent toutes sur ce schéma fonctionnel

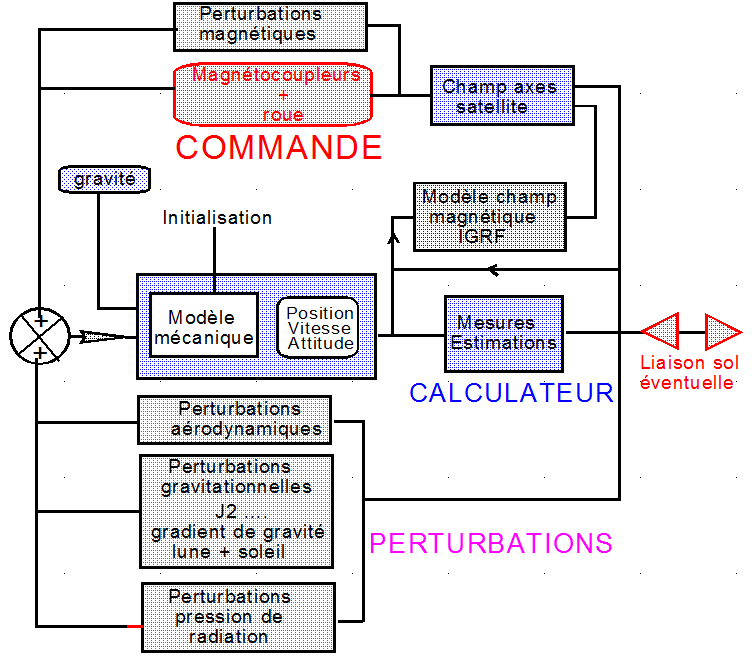
Avec:

- En bleu les modules intégrés calculant ou estimant, après traitement des mesures: position, vitesse, attitude, champ magnétique en axes satellite, connaissant le champ magnétique IGRF de référence, stocké à bord. Le calculateur et séquenceur programment en continu la commande des magnétocoupleurs et d'une roue tangage.

- En rose ce qui est considéré comme perturbations dans le vol réel, s'exerçant bien évidemment naturellement sans calcul. Ces perturbations sont cependant approchées au mieux dans les simulations de validation de la commande, et dans ce cas là ces perturbations sont dans la boucle du calculateur de simulation.

- En rouge la commande élaborée en continu par le calculateur de bord. En cours de vol certaines données peuvent être transmises au sol ou reçues du sol, pour information ou restitution d'orbite.

I SIMULATION ( totale2.m initialisée par totdatNP.m ou totdatP.m) :

NP veut dire champ non pulsé et P champ pulsé

a) Ce que fait la simulation ( mise en équations sous quaternion d'attitude ):

Elle est bâtie sur 2 modules de régulation ( non compris les termes provenant des caractéristiques inertielles )

1 - Le module initial, en provenance de reg_derB.m , régulation basée sur la dérivée de B dite Bpoint, infaillible, qui ne peut jamais être mise en défaut ( pas de singularité physique et pas de singularité mathématique liée aux paramètres angulaires ). 

Pour l'instant la possibilité d'adjoindre la roue sur le tangage, n'est pas envisagée. C'est un sujet d'étude à suivre.

C'est la première phase dite de " détumbling " qui dure environ 2700 - 870 = 1830 s . Le satellite n'est pas encore au niveau du pôle Nord. Elle se termine sur un ordre de seuil de vitesse ( à choisir, il est fixé par défaut actuellement à 0.003 rd/s ( en gros 1 tour en 30 mn )).

2 - Un deuxième module, en provenance de reg_acq1.m, qui poursuit l'acquisition, jusqu'à réduire les angles, sous un seuil à fixer en fonction des spécifications de la mission, pour moi, j'ai choisi le seuil de 1°.

b) Résultat  pour une simulation: ( ce sont les sorties in fine dans l'espace Matlab )

*************** PRINCIPALES DONNEES DE LA SIMULATION ***************
                                        Nanosatellite CASAASAT

simulations total0.m ou total1.m ou total2.m
initialisées par totdatNP.m ou totdatP.m etc...
------------------------------------
***********************************************************************

Latitude d'injection = 70 °
Heure d'injection = 869 s Avec rappel --> Heure =0 au survol équateur
Heure de fin de Tumbling = 2861 s, soit 1992 s, après l'injection
Heure fin d'acquisition fine = 3282 s, soit 1291 s, après la fin du tumbling

--------------------- RESPECT DES SPECIFICATIONS ------------------------
Moment magnétique maximum bobine = 0.2 Am²
Vitesse angulaire de coupure detumbling = 0.003 rd/s
Ecart maximum de pointage en acquisition fine = 0.01745 rd
Couple maximum sur la roue = 4e-006 Nm
Nombre minimum de points stockés pour les courbes = 3e+004
Consigne de tangage = 0 rd
Consigne de roulis = 0 rd
Consigne de lacet = 0 rd
Simulation avec champ non pulsé

--------------------- COEFFICIENTS DES REGULATIONS ------------------------
ROULIS
K_PID_ROULIS= 3.2e-006 SI
F_PID_ROULIS = 0.000256 SI
GAIN_ROULIS = 6.25e+004
LACET
K_PID_LACET= 1.375e-006 SI
F_PID_LACET = 0.000395 SI
GAIN_LACET = 6.25e+004
TANGAGE
K_PID_TANGAGE= 3.6e-006 SI
F_PID_TANGAGE = 0.00036 SI
GAIN_TANGAGE = 8.25e+004
NB : Les coefficients peuvent etre modifiés dans le module dédié de la simulation
ou directement dans l'espace Matlab

--------------------- VALEURS INITIALES ------------------------
Angle de roulis = 0.1 rd Vitesse de roulis = 0.06 rd/s
Angle de tangage = -0.1 rd Vitesse de tangage = 0.05 rd/s
Angle de lacet = 0.05 rd Vitesse de lacet = 0.01 rd/s
--------------------- PARAMETRES DU PULSE ------------------------
periode = 10 s temps d'action = 9 s

--------------------- FONCTIONNEMENT DE LA ROUE ------------------------
Vitesse initiale = 0 rd/s ou 0 to urs/s
Vitesse finale = -1.699 rd/s ou -16.23 tours/mn

--------------------- TRANSMISSION EVENTUELLE DE DONNEES ------------------------
Vecteur à 7 composantes initialisant l'intégration par le quaternion d'attitude en repère orbital

etat_init = [0.05905 0.05177 0.0048 0.9971 0.05115 0.04865 -0.02743]

Rotation absolue initiale en repère satellite: p=u(1) q=u(2) r=u(3)
Quaternion d'attitude initiale par rapport au repère orbital:Q =[u(4) u(5) u(6) u(7)]


Vecteur à 7 composantes de la configuration finale ( variable u=initpqrQ_final)

etat_final = initpqrQ_final = [0.0001287 0.001136 0.0001913 1 -0.0008927 -0.003816 -0.007797]

Instant de fin de simulation Tf = 3282 secondes
Rotation absolue finale en repère satellite: p=u(1) q=u(2) r=u(3)
Quaternion d'attitude finale par rapport au repère orbital:Q =[u(4) u(5) u(6) u(7)]

Vecteur à 8 composantes de la simulation  ( variable u=initpqrQ stockée dans initpqrQ.mat)
u(1) le temps
u(2:4) la rotation absolue en axes orbitaux
u(5:8) le quaternion d'attitude du satellite par rapport au repère orbital

********************************* FIN DES SORTIES ***********************************

La régulation est parfaite ( il faudrait vérifier que la robustesse du résultat ne dépend pas des conditions initiales )

En 2800 secondes environ après l'injection, l'affaire est réglée, et les vitesses et positions correctes pour travailler. Le satellite est passé vers 1500 s au niveau des pôles et redescend vers l'équateur qui sera atteint 300 secondes après l'acquisition.

Il aura fallu moins d'une demi-orbite pour stabiliser le satellite.

Ci-dessous la phase finale est traitée sévèrement (gains importants ). Les courbes donnent l'allure d'un retour voisin du régime critique.

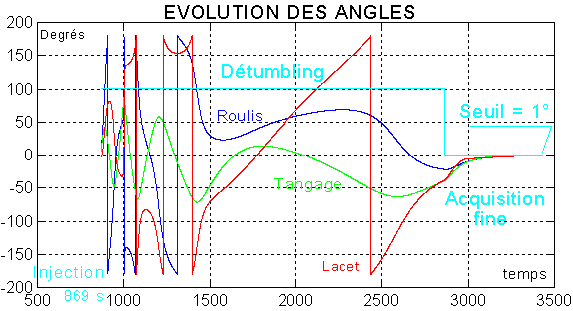
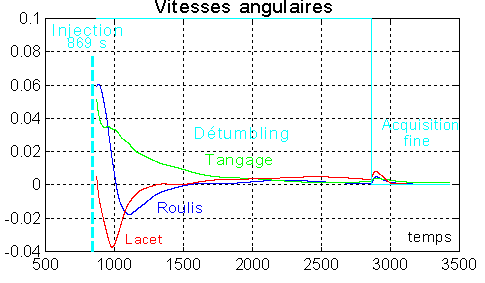
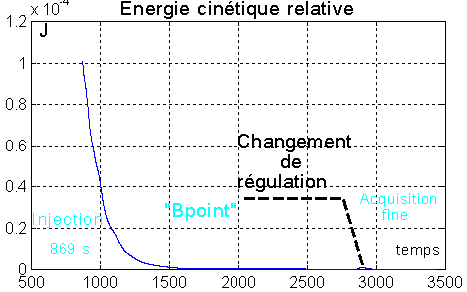
Une preuve de stabilisation, dans la bonne orientation, est l'accord des composantes du champ sur Y du repère orbital et sur y du repère satellite

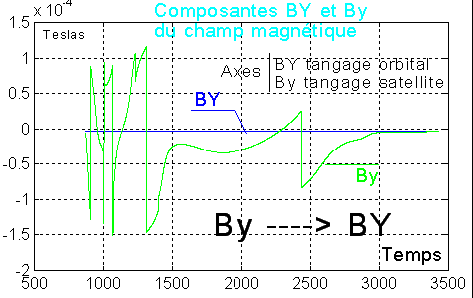
III PROBLEME POSE PAR LE FONCTIONNEMENT DE LA MESURE MAGNETIQUE:

C'est la première approche du respect des spécifications techniques, dont une : 

On peut imaginer de faire agir les couples de commande des actuateurs, sans pour l'instant manipuler les composantes du champ.

Durant un temps temps_action  ----> typiquement 9 s

Périodiquement de période nommée periode ---> typiquement 10 s

Avec un temps d'arrêt pour les mesures de periode - temps_action ---> typiquement 1 s

1°) LA CONTRAINTE PRINCIPALE :

Le système de mesure des composantes du champ magnétique et de sa dérivée, exprimées sur les axes satellite, demande un environnement sans émission de champ magnétique parasite.

L'utilisation des magnétocoupleurs doit donc être suspendue pendant les périodes de mesure.

Par contre le moment magnétique interne ne gêne absolument pas la mesure. Heureusement !

Il nous faut donc imaginer comment simuler ces périodes d'arrêt, celle de mesure et d'en tester les conséquences sur la robustesse de la simulation.

Il faut au départ connaître au minimum;

   Le temps Ta d'arrêt

   La durée Tu d'utilisation des mesures faites périodiquement à la période T = Ta + Tu

2°) ESTIMATION DU CHAMP ET DE LA DERIVEE : objet de la simulation isolée ( pour la mise au point ) regpulse/b_estim.m initialisée par totdatP.m

Fichiers récupérables

Pour la mission réelle les valeurs mesurées sont fournies par les appareils de mesure et transmises au calculateur, ce sont directement les composantes en axes satellite.

Le champ magnétique B et sa dérivée sont calculés à intervalles réguliers distants de T = Ta + Tu.

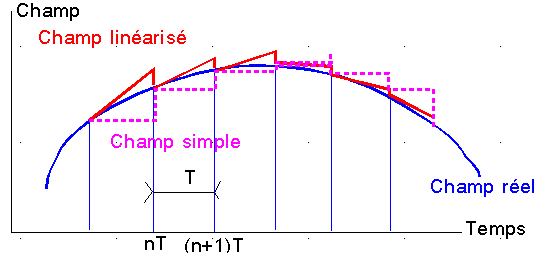
Nous supposons que la mesure est faite au milieu de l'interruption et disponible dès la fin de l'interruption, soit à t = nT+Ta/2.

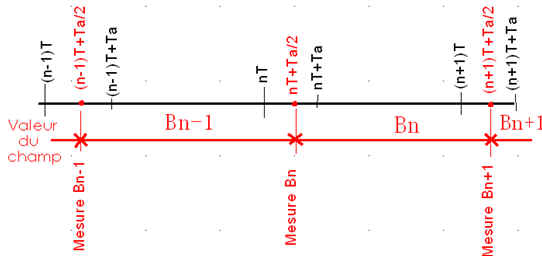
On note :

- B le champ réel

- Bm le champ mesuré en t = to+Ta/2, e₁ (t₀) et e₂ (t₀) sont des termes d'erreurs ( peut-être bruités ) ( pour moi les erreurs ne sont pas prises en compte, ne les connaissant pas !!! )

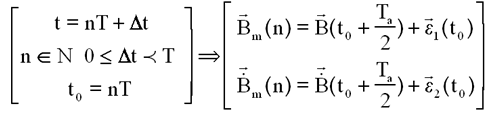
a) Approche simple du champ magnétique: On peut alors, dans un premier temps donner une expression du champ et de sa dérivée, dans l'intervalle de temps où ils seront utilisés. On conserve de t = nT+Ta/2 à t = (n+1)T la valeur mesurée en t=nT+Ta/2 et pour la dérivée, les valeurs estimées de B et de sa dérivée sont notées avec un"chapeau"

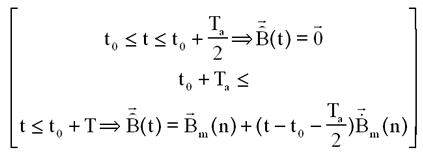
avec l'allure suivante

b) Approche plus fine du champ magnétique:

Au mieux, on peut approcher le champ par la technique d'Euler, en utilisant une variation linéaire sur l'intervalle nT+Ta/2 (n+1)T grâce à la dérivée qui est connue en début d'intervalle:

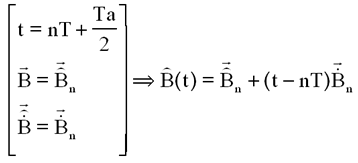
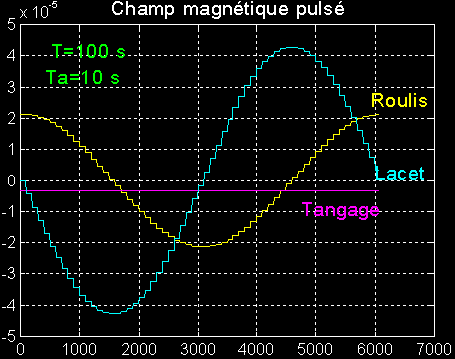
Les graphes qui suivent montrent que le champ pulsé linéarisé est une excellente approche du champ réel à

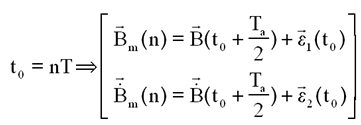
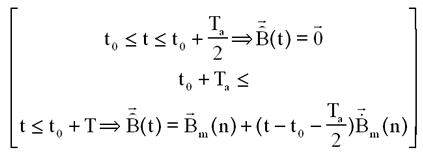
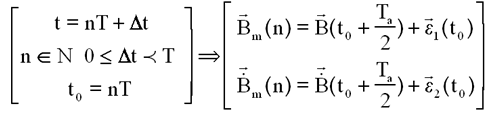
Ecarts absolus maximum de 3 e-7 teslas

Conclusions: en ce qui concerne les valeurs du champ, l'approche linéarisée est de loin préférable et probablement sans conséquences sur les régulations. Les erreurs sur les composantes, par rapport au modèle simple, ont été divisées par 10.

De plus les fonctions ne font pas apparaître de sauts, ce qui augure d'un bon comportement des simulations.

c) Etude particulière de la dérivée: elle pourrait ressemble à la précédente, encore faudrait-il estimer la dérivée seconde du champ?

Cas le plus simple, on conserve la valeur mesurée à t = nT+Ta/2, et on obtient ces courbes en escalier.

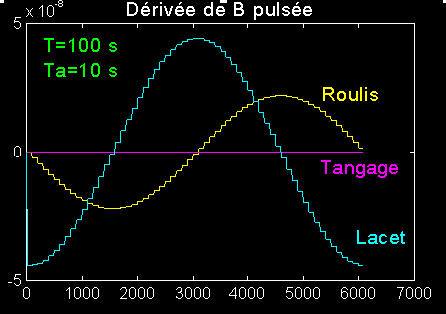
Un agrandissement permet de mieux apprécier l'erreur commise et d'en déduire qu'elle diminue avec la période, ce qui est évident, mais impose la période la plus courte possible, en accord avec le fonctionnement de la mesure. 

Sur l'exemple l'erreur est de 5% pour une période de 100 s sur lesquelles la mesure prend 10 secondes.

Une idée peut-être serait de stocker 2 mesures consécutives de la dérivée, d'en tirer une estimation de la dérivée seconde et donc de linéariser au plus près la dérivée ( les escaliers seraient minimisés )

3°) ESTIMATION DU CHAMP, DE LA DERIVEE  ET SON UTILISATION: 

La simulation de l'approche du champ et de sa dérivée est b_estime.m initialisée par totdatP.m ( P indique pulsé )

La fonction est résumée dans le bloc 

Retrouver les fichiers

a) Le calcul des couples de commande:

Rappelons que les champs mesurés ( champ magnétique ou sa dérivée ) servent à élaborer les couples de commandes des magnétocoupleurs ou de la roue, dans toutes les simulations. En clair les formules montrent l'utilisation mélangée des 2 champs, réel et simulés = mesurés

a) La suppression des régulations:

Durant la simulation, les calculs précédents doivent être interrompus durant l'intervalle de mesure, de restitution des champs et d'élaboration des commandes.

Ce temps d'arrêt vaut Ta =10 s sur  une période de 100 s, et pour l'instant je n'ai pas d'autre information.

La simulation, se fera en sortie du système différentiel, au niveau des couples de commande:

- En gardant les perturbations réelles

- En gardant les couplages roue satellite, mais sans accélérer la roue

- En multipliant toutes les commandes par une fonction "pulse" nulle entre t et t+Ta, valant 0 entre t+Ta et t+ T.

IV SIMULATION TOTALE EN REGULATION DE Philippe LAURENS :

Cette simulation est tellement importante que je préfère lui réserver une rubrique spéciale Voir réduction des vitesses et acquisition en une seule opération

********************************************  Fin *********************************************

Juin 2014