ESSAI DE REGULATION LAURENS + UNE ROUE DE REACTION
POUR CONTRER LA ROTATION COLINEAIRE AU CHAMP MAGNETIQUE
A un instant t quelconque du tumbling, le satellite traité en mode "Bpoint" ou presque équivalent "Boussole" voit sa rotation absolue diminuer en partie, par la décroissance continue de la rotation transverse au champ magnétique B régnant à la position du satellite.
Par contre la partie WB de cette rotation parallèle à B n'est pas contrôlable par les magnétocoupleurs. M Laurens indique donc que c'est la roue qui doit se charger ( peut-être? ) de cette composante. Or la roue ne peut créer qu'un couple de réaction d'axe y qui a peu de chance de porter la rotation WB , elle ne pourra intervenir que comme complément dans un couple réalisable avc des magnétocoupleurs.
Donc essai d'utilisation de la roue pour participer à la réduction de la rotation parallèle à B. Cette tentative a le mérite de montrer une autre régulation, mais elle ne permettra pas la convergence des angles, car le satellite pourrait se retrouver arrêté en fixité inertielle, sans rotation mais en orientation quelconque.

La roue peut cependant pariciper à un couple C2 opposé à la rotation WB , de la forme C2 = - K WB , qui va réduire cette composante, si on ajoute un moment C1 ( normal à B ) déstabilisant et créateur d'une rotation transversale parasite, dont devrait se charger la régulation " Bpoint" ou "Boussole", pour peu que le moment magnétique M2 nécessaire soit orthogonal à B ( condition nécessaire ).
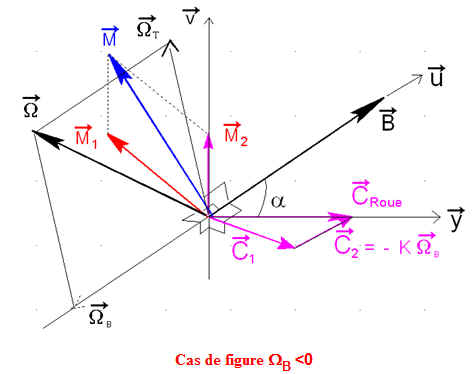
Le lecteur montrera rapidement que le couple C1 est orthogonal à B
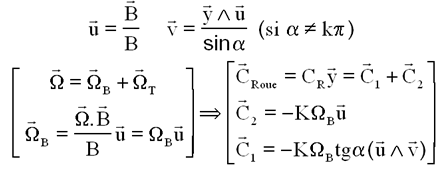
Pour contrer le couple parasite C1, un moment magnétique M2 est nécessaire, il viendra s'ajouter à celui M1 nécessaire pour la régulation "Boussole". Ainsi en créant - C1, il ne restera que la partie utile C2.
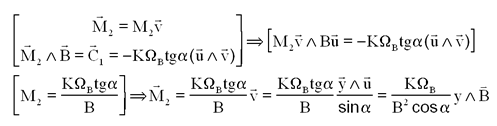
La régulation va donc utiliser les magnétocoupleurs de moment complet M et un couple roue CRoue sur y tels que
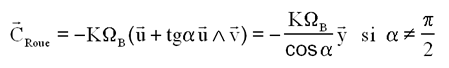
Le moment magnétique à construire est M

Résumons pour vérification :
Nous créons :
- Un moment magnétique M = M1 + M2, normal à B qui interagit avec B pour créer :
- Un couple roue CR y sur l'axe y
- Le couple C2 s'opposant à WB . Ceci pour réaliser le couple de commande Ccom

SIMULATION : /../ nanosat3/boussol2.m avec initialisation par laurdat1.m |
La simulation complète donne un excellent résultat sur les vitesses, par contre les angles ne sont pas stabilisés, je m'y attendais un peu car la régulation ne porte que sur les vitesses, à moins qu'une vitesse initiale importante de la roue modifie la donne ( à voir )
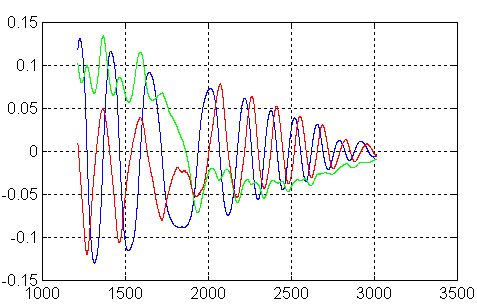
Seuil de vitesse fixé à 1 e-2 rd/s soit environ 0.6 °/s

L'énergie diminue dans le sens souhaité
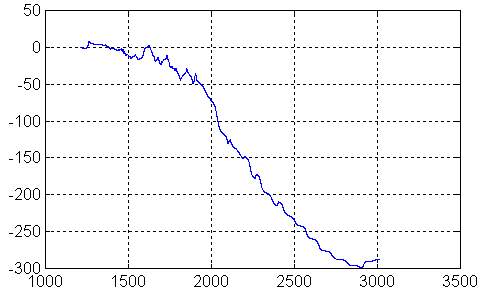
La roue prend peu de tours
Poursuite de la simulation pour tenter d'acquérir les angles :
ESSAI 1 :
Avec un seuil de vitesse plus bas ( 0.001 rd/s angles toujours aléatoires )
ESSAI 2 :
Avec une roue initialement en rotation résultat catastrophique pour 300 rd/s:
Avec une roue initialement en rotation résultat un peu meilleur pour 100 rd/s:
Avec une roue initialement en rotation résultat surprenant pour -100 rd/s, mais angles non acquis
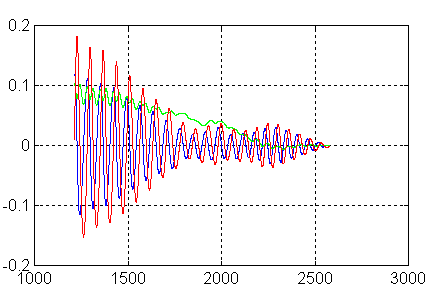
Avec une roue initialement en rotation résultat surprenant pour -50 rd/s, mais angles non acquis
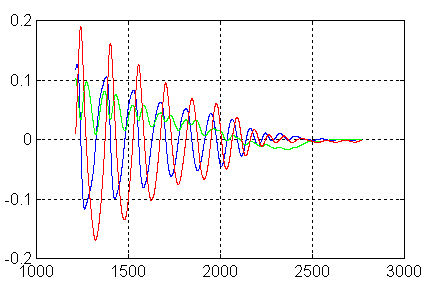
Malgré tout, on voit les vitesses avoisiner 0 et donc les angles, pratiquement se stabiliser sur une position aléatoire, ce qui m'amène à penser qu'un rappel minime sur les angles pourrait pourrait donner l'acquisition. Après coup, la non acquisition des angles semble normale, puisqu'on ne s'est occupé que des vitesses angulaires.
Je vais donc essayer un rappel de type PD, sur les angles , en parallèle et complément de la régulation de Laurens.
************************* Fin de page ***************************