|
EXEMPLES NUMERIQUES |
|
|
EXEMPLES NUMERIQUES |
|
EXEMPLE I
: (Réalisé en grande partie par un internaute désireux de vérifier la théorie des quaternions)Il est envisagé d'utiliser les trois rotations résultant des
angles d'Euler classiques y, q, j .y
= Psi = 35°, q = Théta = -70°, j = Phi = 10°CALCULS A FAIRE
:1°) Matrice de passage du repère initial au repère final :
Avec les notations de programmation suivantes
CP=cos(Psi);SP=sin(Psi);CT=cos(Theta);ST=sin(Theta);CF=cos(Phi);SF=sin(Phi);
On trouve
Rot_Mat=[ CF*CP-CT*SP*SF -CP*SF-CF*CT*SP ST*SP;
CF*SP+CP*CT*SF -SF*SP+CF*CT*CP -ST*CP;
SF*ST ST*CF CT]
Numériquement :
Rot_Mat = [ 0.7726 -0.3354 -0.5390
0.6135 0.1763 0.7698
-0.1632 -0.9254 0.3420 ]
2°) Quaternion associé :
Quaternion = [ 0.7568 -0.5600 -0.1241 0.3135 ]
3°) Quaternions associés à chaque rotation élémentaire:
Q1 = Quat_Psi = [ 0.9537 0 0 0.3007 ]
Q2 = Quat_Theta = [ 0.8192 -0.4698 -0.3290 ]
Q3 = Quat_Phi = [ 0.9962 -0.0470 0.0671 0.0298 ]
4°) Quaternion produit Q= Q3*Q2*Q1
Q = [ 0.7568 -0.5600 -0.1241 0.3135 ]
5°) Matrice de passage déduite de ce quaternion
On utilise la formule établie dans le cours :
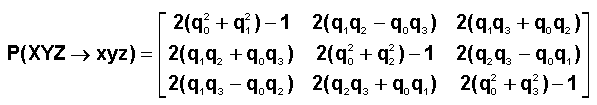
qui donne un résultat identique à celui de 1°) , confirmant la théorie.
6°) Eléments de la rotation globale :
Le quaternion Q symbolise une rotation d'angle
a et d'axe u.Le calcul donne :
Axe u = -0.8567 I -0.1899 J+ 0.4796 K
L'angle de rotation en degrés vaut
a = 81°.63467°) PROGRAMME DE VERIFICATION SOUS MATLAB :
Vous pouvez récupérer un programme et une fonction indispensable à ce programme dans
TestQuat.zip8°) VERIFICATION SUPPLEMENTAIRE :
Avec les relations:
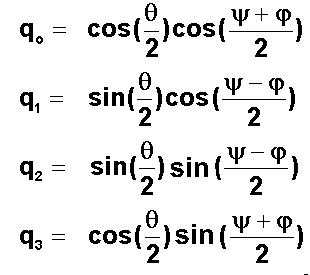
On retrouve les mêmes résultats Q=[0.757 -0.559 -0.124 0.313]
![]()