![]()
(Traitement du projet
possible par tout langage de programmation)
I PRESENTATION:
1°) Généralités :
On
s'intéresse ici au problème du retour, sur une planète, d'un engin spatial, par
une méthode passive, où la dépense d'énergie est naturelle, sans intervention
d'un moteur pour la partie principale du freinage. Classiquement, ces retours
utilisent donc le freinage aérodynamique dans l'atmosphère de la planète.
On
ne compte plus les retours atmosphériques vers la terre, qui sont devenus
routiniers tels ceux de la navette US ou les équipages de la station MIR et
maintenant de la station spatiale internationale (ISS). D'autres restent
historiques comme ceux de Gagarine ou de Glenn. Bientôt, probablement, cette
technique sera utilisée, pour l'arrivée sur mars de futures explorations
spatiales.
La
recherche de documents devrait faire partie du projet, pour illustrer et
conforter les résultats et aussi permettre une meilleure compréhension du
phénomène ainsi qu'une analyse plus fine des éventuelles erreurs que vous
pourriez commettre.
2°)
Conditions de la rentrée:
Pour
ce projet, par souci de ne pas compliquer les équations, on se limitera à une
rentrée plane, équatoriale, dans le sens de la rotation terrestre, pour limiter
au maximum la vitesse relative VR de rentrée.
La
recherche de documents devrait faire partie du projet, pour illustrer et
conforter les résultats et aussi permettre une meilleure compréhension du
phénomène ainsi qu'une analyse plus fine des éventuelles erreurs que vous
pourriez commettre.
2°) Conditions de la rentrée:
Pour
ce projet on se limitera à une rentrée plane, par rapport à la terre supposée
fixe ( non prise en compte de sa rotation axiale ), on confondra donc vitesse
absolue et vitesse relative.
L'orbite
initiale de travail est supposée circulaire d'altitude Zo = 300 km.
Une manoeuvre de déorbitation, supposée optimale, c'est à dire de
freinage optimal, est réalisée grâce à l'usage d'un moteur fonctionnant en
rétrofusée ou pratiquement et délivrant un incrément de vitesse DV, opposé à la vitesse ( c'est généralement la
solution optimale pour les orbites basses et des angles de rentrée faibles <
10°).
La
rentrée est considérée comme effective à partir de l'altitude ZE =
80 km du sol terrestre.
II FIGURES ET TRAITEMENT DES EQUATIONS :
1°) Figure de la déorbitation:
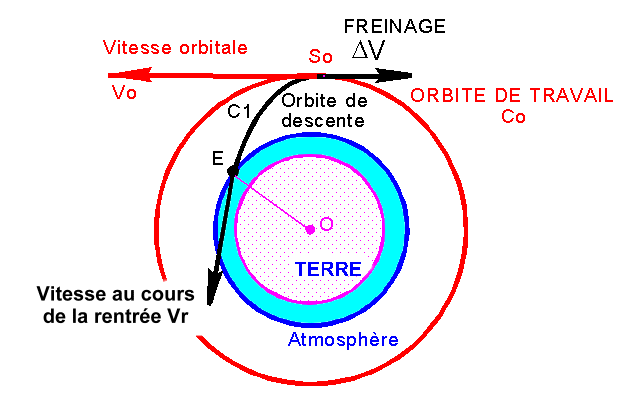
Vous
calculerez, pour cette rentrée, le freinage DV
nécessaire pour obtenir un angle de rentrée gE ou bE donné ( pente de la vitesse
relative sous l'horizontale ). On donne mT = 39.86
104 km3s-2 et le rayon de mars RT =
6378 km
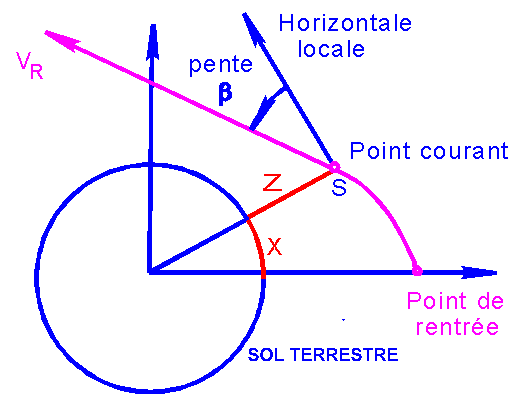
2°) NOTATIONS
ET FIGURE:
V
: Vitesse
b ou g : Pente de la vitesse relative
(positive sous l'horizontale)
Z
: Altitude sol
X(t)
ou D(t) : Distance horizontale parcourue depuis la verticale du point de
rentrée.
i
est l'incidence ( i>0 vol sur le ventre, i<0 vol sur le dos). Elle n'est
pas visible sur la figure, c'est nous le rappelons, l'angle entre la vitesse et
l'axe aérodynamique du corps de rentrée. L'incidence permet de moduler la
finesse, mais vous n'aurez pas capsule en incidence.
La
modélisation de l'atmosphère devra naturellement être celle de Chapman pour toute la partie principale de la
rentrée, c'est à dire entre 5 km et 80 km.
III DONNEES, CONDITIONS LIMITATIVES ET RESULTATS :
1°) Conditions de vol :
Vous
adopterez les conditions de vol suivantes:
Z
< 5 km Ouverture des parachutes, la
théorie de Chapman n'est plus applicable
Z
= 80 km Entrée ou sortie de l'atmosphère
(rebonds éventuels en trajectoire képlérienne).
Vous
tiendrez compte aussi de la condition f tgg
< 0.1
2°) Planeur utilisé :
M
= 12760 kg Masse du corps de rentrée
S
= 55 m2 Surface du maître couple
CX
= 1.16 Coefficient aérodynamique de
traînée en hypersonique
CZ Coefficient aérodynamique de portance
f
= CZ/CX Finesse
aérodynamique, que vous pourrez faire varier
NB:
0 =< f <= 0.6 la finesse peut varier grâce au pilotage.
VE,
gE = bE, Vitesse absolue d'entrée dans l'atmosphère à 60 km , angle de rentrée à calculer ou à choisir
NB: Vous pourriez aussi essayer une rentrée avec une cabine du
genre Apollo, avec SCX/M = 0.0032 et finesse fmax = 0.35.
3°) RESULTATS A FOURNIR :
a) CLASSIQUES EN FONCTION DU TEMPS:
Vous
fournirez notamment :
Un
profil de vol avec la portée X en abscisse et l'altitude Z en ordonnée
Les
allures de l'altitude, de la décélération et de la vitesse en fonction du
temps, pour diverses rentrées.
Des
comparaisons de ces caractéristiques en liaison avec le rapport SCx/M ou
l'angle de rentrée.
b) En
fonction de la VARIABLE DE CHAPMAN :
De
nombreuses publications utilisent pour le tracé des courbes une variable u
appelée variable de CHAPMAN ( chercheur qui s'est beaucoup intéressé aux problèmes de
rentrée).
Cette variable est sans dimension est le quotient de la vitesse absolue
horizontale et de la vitesse absolue d'orbitation circulaire là où est la
capsule, comme cela a été rappelé dans le cours cité ci-dessus.
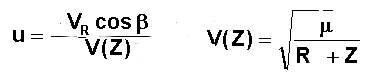
Vous
éviterez l'abus de tableaux de résultats , ceux que vous fournirez seront les
plus significatifs et soigneusement annotés.
Vous
étudierez en particulier:
L'influence
de l'angle de rentrée sur la décélération maximum
o
à
finesse nulle et un angle de rentrée variant de 0 à 6°.
o
à
finesse non nulle entre 0 et 0.6 et un angle de rentrée fixé.
o
L'influence
de la finesse sur les profils Z = Z(u), pour divers cas de rentrée.
o
La
portée horizontale et l'influence des divers paramètres sur cette portée.
Vous
commenterez les résultats et notamment les comparerez avec ceux que vous aurez
pu trouver dans les documentations
Un
exposé sur les rentrées avec vols humains serait le bienvenu et intéresserait
l'auditoire.
NB:
Un autre groupe étudie peut-être une rentrée par intégration directe des
équations du mouvement. Comparez et commentez vos résultats respectifs
éventuels.
4° ) DOCUMENTS FOURNIS :
Ci-dessous deux graphiques concernant une rentrée en atmosphère terrestre
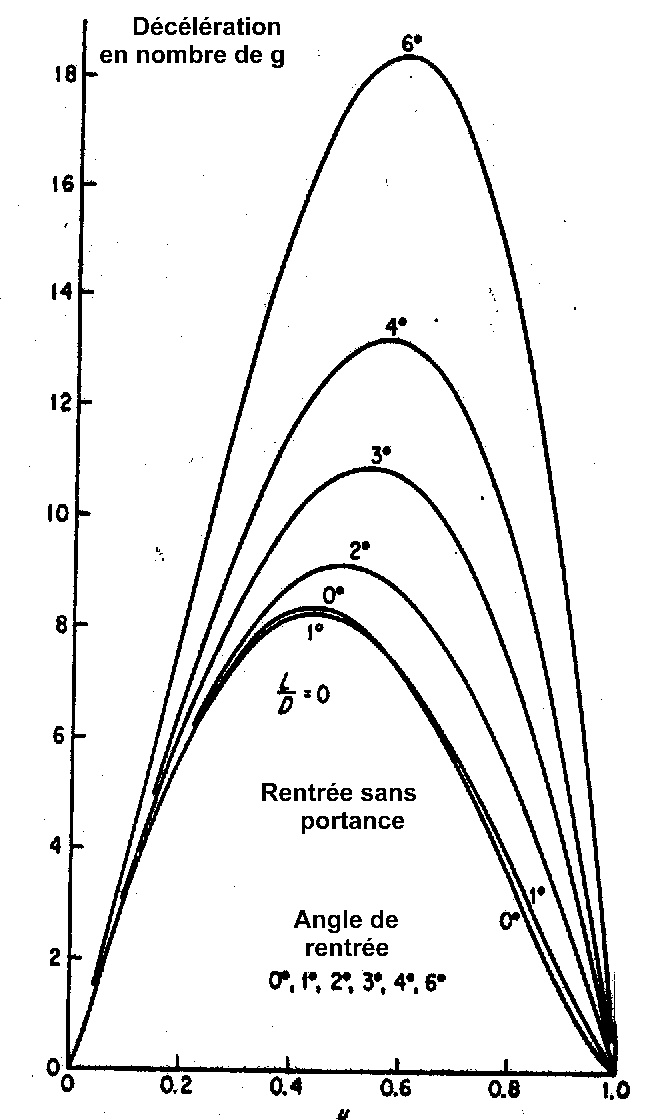
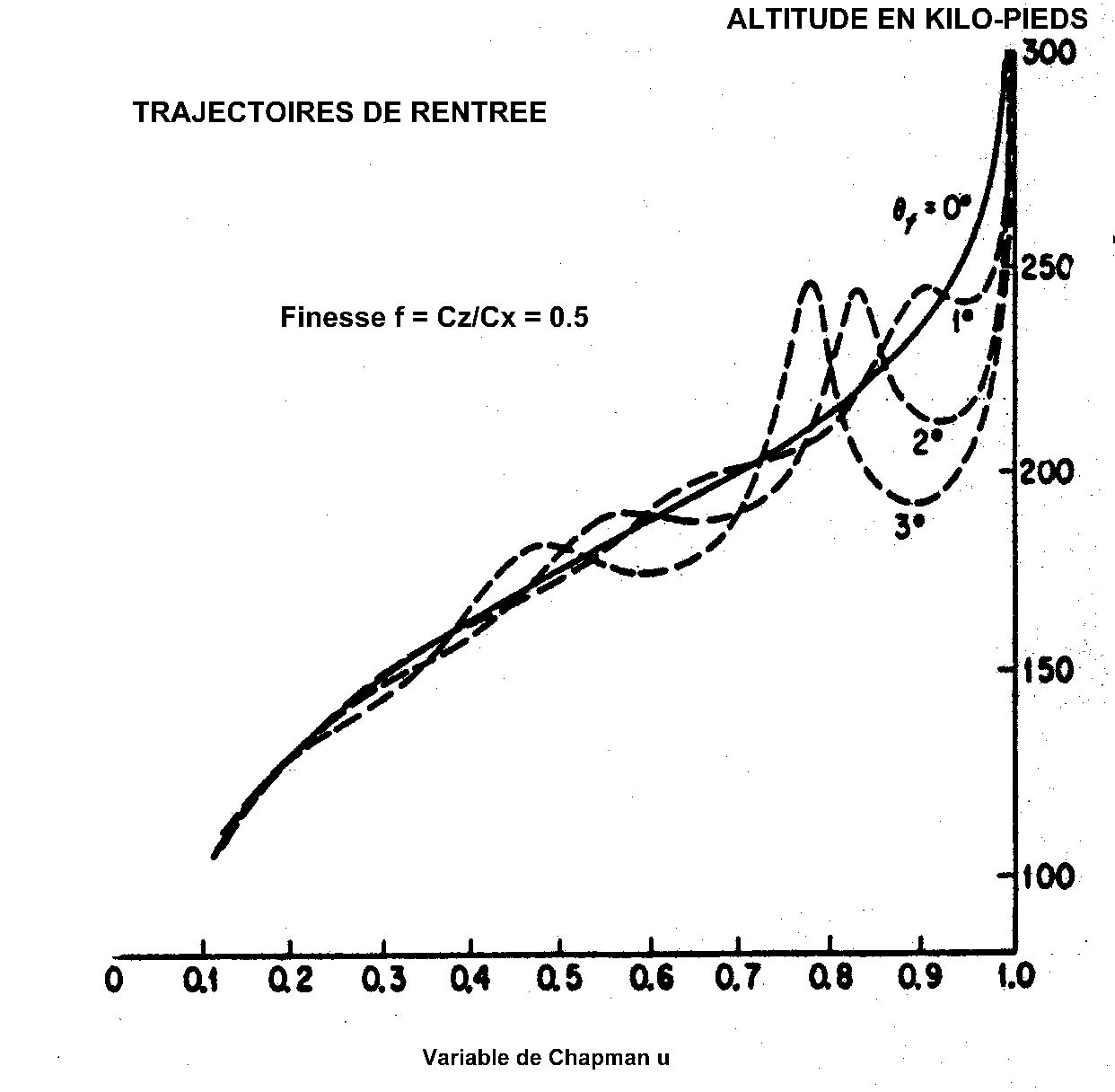
Si
l'angle de rentrée est supérieur à 6°, vous essaierez de retrouver la
décélération maximum, pour peu que vous connaissiez la vitesse d'entrée et la
loi de variation de la masse volumique de l'air, en utilisant la théorie d'ALLEN que vous découvrirez dans le cours.
Aide à la mise au point:
Si vraiment vous avez besoin de vérifier vos calculs, voici quelques
graphiques qui peuvent vous rassurer.
MODELISATION DE L'ATMOSPHERE :
Vous
devrez aussi modéliser l'atmosphère standard, suivant la simplification de
Chapman:
r
= rho(Z) Masse volumique de l'air à l'altitude Z, soit en recherchant des
tables de données pour Z VARIANT de O à 120 km, ou si vous programmez en
Pascal, avec l'unité AIRSTAND, ou avec le tableau ci-après tiré d'une
programmation et que vous pourrez adapter à votre usage. Vous ferez au mieux
entre 5 et 80 km.
BEGIN
if ((z>=0) and (z<17)) then
rho=1.293*exp(-0.1202*z) else
if ((z>=17) and (z<22)) then
rho=3.8923*exp(-0.185*z) else
if ((z>=22) and (z<25)) then rho=1.3553*exp(-0.13707*z)
else
if ((z>=25) and (z<30)) then
rho=2.11643*exp(-.15489*z) else
if ((z>=30) and (z<35)) then
rho=3.51386*exp(-0.1718*z) else
if ((z>=35) and (z<40)) then
rho=1.34076*exp(-.14426*z) else
if ((z>=40) and (z<45)) then rho=1.04184*exp(-.13544*z)
else
if ((z>=45) and (z<50)) then
rho=0.69735*exp(-.12904*z) else
if ((z>=50) and (z<60)) then
rho=0.6188*exp(-0.12664*z) else
if ((z>=60) and (z<70)) then
rho=0.45374*exp(-0.12148*z) else
if ((z>=70) and (z<80)) then
rho=5.14519*exp(-0.15616*z) else
if ((z>=80) and (z<100)) then
rho=42.8456*exp(-0.18266*z) else
if ((z>=100) and (z<110)) then
rho=100.01581*exp(-0.1913*z) else
if ((z>=110) and (z<120)) then
rho=11.2811*exp(-0.16712*z-0.4772)
else rho=0;
END;
GUIZIOU Robert décembre 2001, sept , sept
2011