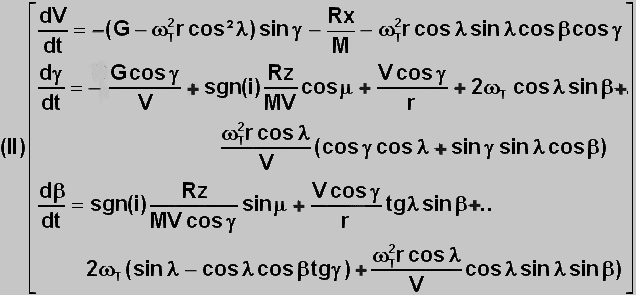ARC ATMOSPHERIQUE D'UN RETOUR VERS UNE CIBLE TERRESTRE

(Traitement du projet possible par tout langage de programmation)

I PRESENTATION :

1°) Généralités :

On s'intéresse ici au problème au retour et à la rentrée atmosphérique sur Terre, d'un engin spatial non motorisé, la partie principale du freinage est réalisé par la traînée. Sans aucun doute, l'arrivée future d'un planeur sur mars devra et pourra utiliser un freinage aérodynamique dans l'atmosphère de cette planète.

Souvenez vous de la sonde PATHFINDER que les spécialistes du JET PROPULSION LABORATORY de la NASA ont posé sur le sol de Mars en 1997, vous trouverez plus loin une documentation la concernant.

Vous trouverez les détails des calculs et les équations exactes de la rentrée dans un cours spécifique: arc_atmo.htm

Les perturbations n'y sont pas prises en compte, car la durée de la phase de rentrée est courte, de l'ordre de quelques minutes à quelques dizaines de minutes.

La recherche de documents fait partie du projet, pour illustrer, conforter les résultats et aussi permettre une meilleure compréhension du phénomène ainsi avec une analyse plus fine d'erreurs que vous pourriez éventuellement commettre.

A la différence d'autres projets concernant la rentrée, celui-ci traite le problème dans sa plus grande généralité, et permet connaissant le point d'entrée dans l'atmosphère terrestre de calculer le point de chute, par ses coordonnées géographiques.

2°) Conditions de la rentrée:

L'orbite initiale de travail est donnée, supposée circulaire. Une manœuvre de déorbitation, c'est à dire de freinage, est réalisée grâce à l'usage d'un moteur fonctionnant en rétrofusée et délivrant un incrément de vitesse DV, opposé à la vitesse ( c'est généralement la solution optimale pour les orbites basses et des angles de rentrée faibles < 10°). Vous vérifierez grâce au cours sur la rentrée optimale, qu'il en est ainsi ou alors vous recalculerez complètement cette manœuvre.

On considère que le début de la phase atmosphérique commence au point de rentrée à une altitude sol Z_E = 120 km.

Vous modéliserez l'atmosphère terrestre soit avec un modèle standard, soit un modèle de votre choix, soit en adaptant un programme source en Pascal, parfaitement lisible AIRSTAND.PAS

3°) Orbite de départ:

On suppose que l'orbite de travail est circulaire, est du type de celle de la Station Spatiale Internationale ( ISS ), nous gardons donc les mêmes paramètres orbitaux et ne changeons que la position sur l'orbite, ce qui n'a pas une grosse importance.

Inclinaison i=51°.5680

Excentricité e = 0.0012418 ( orbite circulaire )

Longitude vernale du nœud ascendant : W = 22°.1766

Argument nodal du périgée w = 296°.3716

Moyen mouvement n = 15.61351635 rev/jour

Passage au nœud ascendant 20/12/2002 à 13h 50 mn par exemple.

4°) Point de déorbitation:

Pour commencer, vous traiterez le problème sans vous préoccuper de viser un point de chute prédéterminé et adopterez de déclencher la déorbitation lors d'un survol du nœud ascendant.

En fixant l'angle de rentrée entre 0°et 6°, vous calculerez les coordonnées géographiques exactes du point de rentrée à 120 km du sol terrestre et la vitesse absolue d'entrée V_E, ce qui permettra d'initialiser plus loin la rentrée future en position et vitesse relative.

II FIGURES ET TRAITEMENT DES EQUATIONS :

La manœuvre de déorbitation coplanaire est commune à toutes les misions et relève du cours général sur l'optimisation de la rentrée.

1°) Figure et manœuvre de la déorbitation:

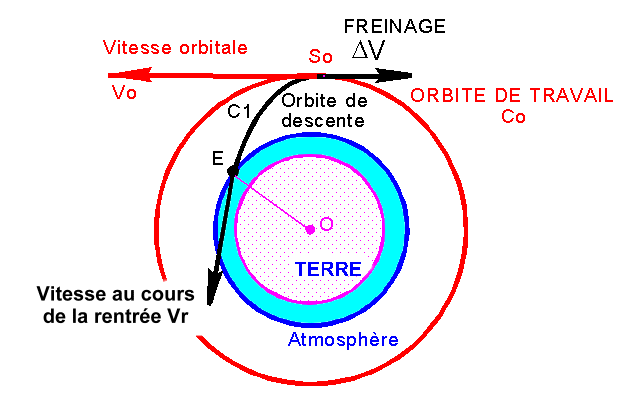
Vous calculerez pour chaque rentrée, le freinage DV optimal ( non obligatoirement de sens contraire à la vitesse ) nécessaire pour obtenir un angle de rentrée absolu g_E ou b_E donné ( pente de la vitesse relative sous l'horizontale ), ne dépassant pas 6°, vous en déduirez alors la pente relative g et la vitesse relative.

2°) SYSTEME DIFFERENTIEL DU MOUVEMENT :

Les équations générales du mouvement ont été établies sur ce site, avec les notations ci-dessous et un nombre minimum d'inconnues de 6 rassemblées dans un vecteur de R⁶ noté Y:

Coordonnées géographiques de positionnement :

L la longitude Greenwich

l la latitude géocentrique équatoriale

r la norme du rayon vecteur

Paramètres de repérage du vecteur vitesse :

V norme du vecteur vitesse de la capsule par rapport à l'atmosphère

g la pente relative du vecteur vitesse relative, angle entre le plan horizontal local et le vecteur vitesse, compté >0 si le vecteur vitesse est au dessus de ce plan

b l'azimut relatif qui, on le rappelle mesuré positivement vers l'Est.

Système différentiel du mouvement, vérifié par Y : voir arc_atmo.htm

III DONNEES, CONDITIONS LIMITATIVES ET RESULTATS :

1°) Conditions de vol :

Vous adopterez les conditions d'arrêt du vol suivantes:

Z < 5 km	Ouverture des parachutes.
V<300 m/s

Z = 120 km Entrée ou sortie de l'atmosphère (rebonds éventuels avec une trajectoire képlérienne ).

En réalité vous constaterez que rien d'important ne se passe en dessus de Z = 60 km. Au dessus de cette altitude les décélérations sont négligeables.

2°) Planeur utilisé :

M = 12760 kg Masse du corps de rentrée

S = 55 m2 Surface du maître couple

C_X = 1.16 Coefficient aérodynamique de traînée en hypersonique

C_Z Coefficient aérodynamique de portance

f = C_Z/C_X Finesse aérodynamique, que vous pourrez faire varier

NB: 0<= f <=0.6 , la finesse pouvant varier grâce au pilotage.

V_E, g_E = b_E, Vitesse absolue et angle absolu d'entrée dans l'atmosphère à 120 km, et angle de rentrée absolu à calculer ou à choisir.

NB: Vous pourriez aussi essayer une rentrée avec une cabine du genre Apollo, avec SC_X / M = 0.0032 et une finesse maximum : f_max= 0.35.

3°) FIN DU VOL :

Lorsque la vitesse tombe en dessous de 300 m/s, des parachutes sont ouverts. Naturellement seule une traînée plus importante est créée, la portance est nulle. Vous ferez donc f=0 dans vos calculs.

Le système de freinage est constitué de 3 parachutes de rayon 12 m chacun ayant un Cx moyen de 1.35.

Le nouveau coefficient de forme avec les parachutes est SCx / M=0.141 environ.

 4 °) RESULTATS A FOURNIR :

Vous éviterez l'abus de tableaux de résultats , ceux que vous fournirez seront les plus significatifs et soigneusement annotés.

a) CLASSIQUES:

Vous fournirez notamment :

Un profil de vol avec la portée X en abscisse et l'altitude Z en ordonnée.

Les allures de l'altitude, de la décélération et de la vitesse en fonction du temps, pour diverses rentrées caractéristiques.

Un profil de vol du type altitude-vitesse Z=Z(V)

Des comparaisons de l'évolution des résultats en liaison avec les variations de SCx/M ou de l'angle de rentrée.

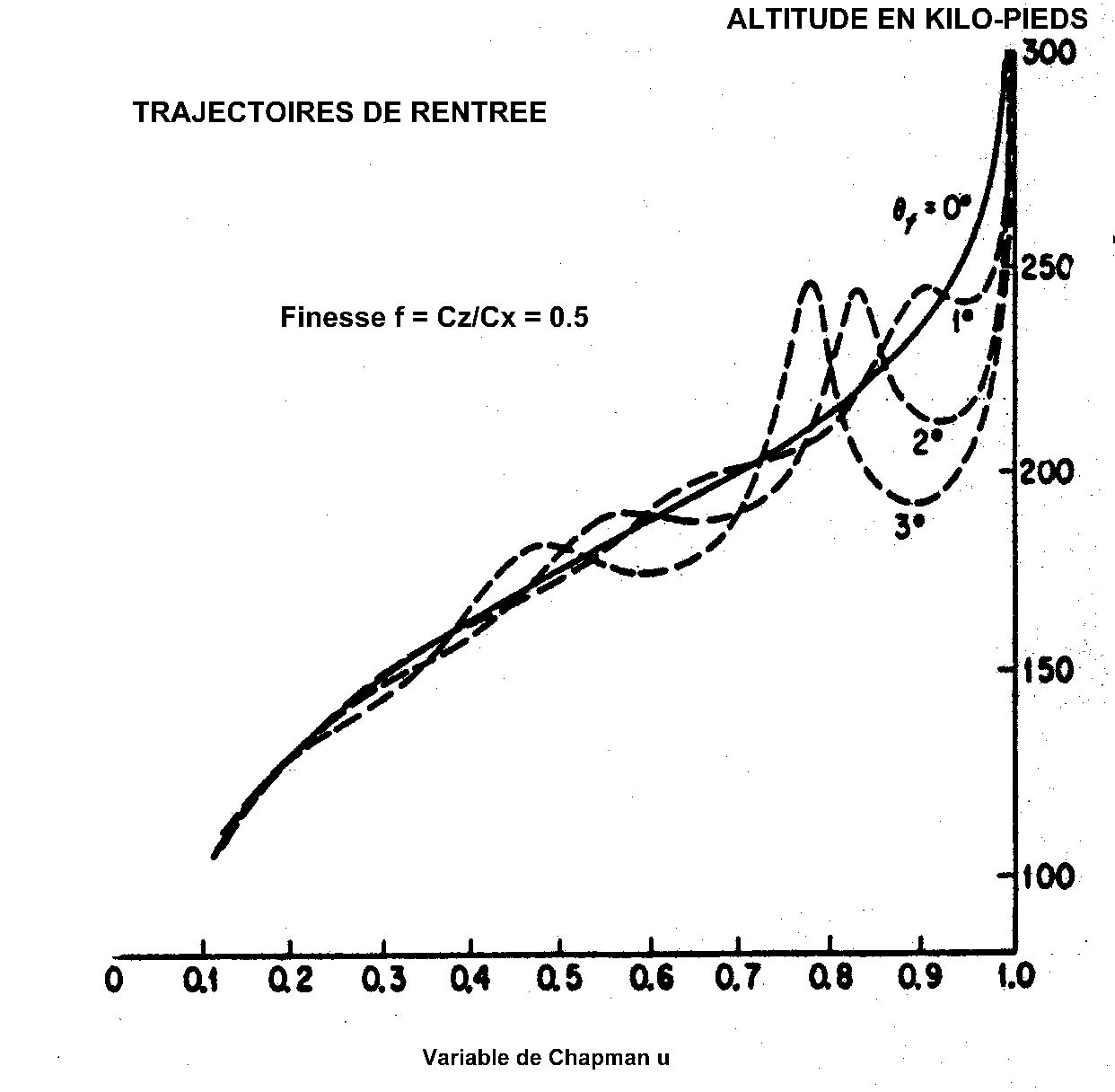
b) En fonction de la VARIABLE DE CHAPMAN :

De nombreuses publications utilisent pour le tracé des courbes une variable u sans dimension, appelée variable de CHAPMAN ( chercheur qui s'est beaucoup intéressé aux problèmes de rentrée ). Cette variable sans dimension est le quotient de la vitesse absolue horizontale Va=Vcosg au point courant et de la vitesse absolue d'orbitation circulaire à l'altitude de la capsule.

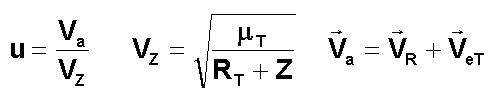
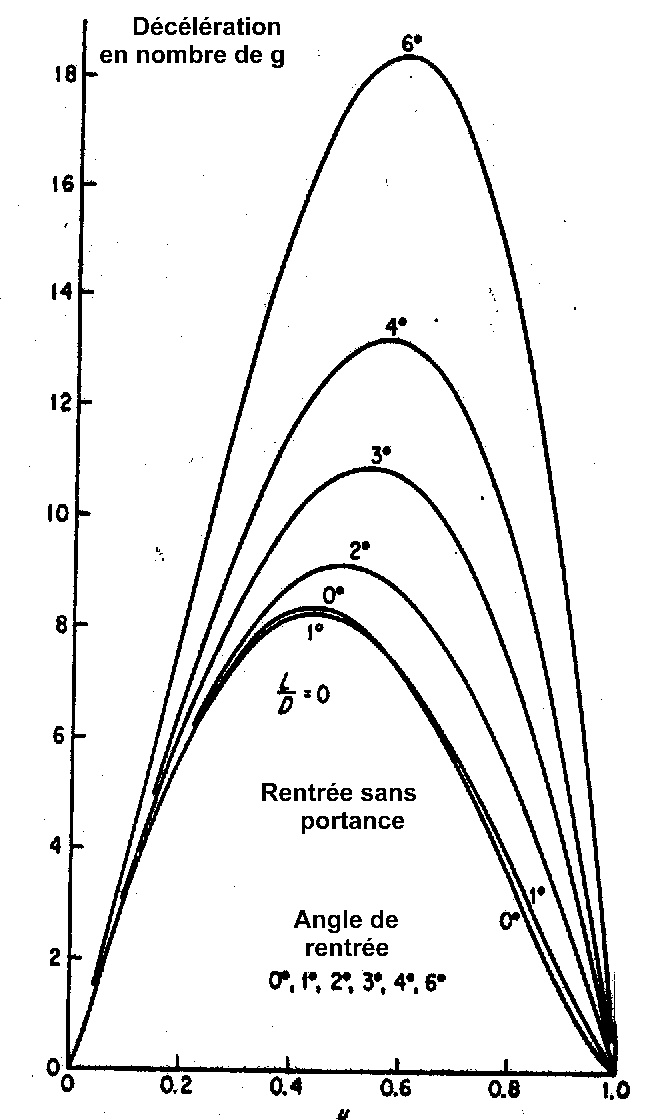
Dans les cas a) ou b) vous étudierez en particulier:

L'influence de l'angle de rentrée sur la décélération maximum

o à finesse nulle et un angle de rentrée variant de 0 à 6°.

o à finesse non nulle entre 0 et 0.6 et un angle de rentrée fixé.

o L'influence de la finesse sur les profils Z = Z(u), pour divers cas de rentrée, avec mise en évidence de rebonds éventuels.

o Les coordonnées géographiques du point de chute.

o La portée horizontale et l'influence des divers paramètres sur cette portée.

o Les tracés d'évolution des divers paramètres en fonction du temps.

o Les profils Z = Z(X) de la trajectoire de rentrée suivant les conditions.

Vous commenterez les résultats et notamment les comparerez avec des données que vous pourriez trouver dans les documentations.

c) Rentrée avec manœuvre en roulis :

En jouant sur l'angle de gite m , essayez de déterminer et visualiser le déport latéral et de préciser la zone pouvant être atteinte par la capsule, les conditions de rentrée variant du balistique à la finesse maximum , et de la gite nulle jusqu'à 90°. Une allure de la zone accessible est attendue.

d) Rentrée à finesse moyenne f = f_max /2 et asservissement de pilotage :

1) Sans déport latéral précisez la trajectoire Z=Z(V) correspondant à cette finesse moyenne, à mi chemin de la rentrée balistique f=0 et de celle à finesse maximum. Gardez en mémoire les coordonnées géographiques du point de chute. Calculez le profil nominal de finesse verticale, comme il est exposé dans le cours arc_atmo.htm

2) On suppose maintenant la présence de perturbations de la haute atmosphère provoquant une augmentation de 10% de la masse volumique de l'air entre 30 et 60 km, et une diminution de 10% entre 20 et 30 km d'altitude. Entre 25 et 35 km d'altitude, des vents violents contraires à V, diminuent la vitesse relative de 100 m/s.

Donner le nouveau point de chute et l'écart kilométrique par rapport au point de chute nominal.

Vous tenterez de mettre en place, grâce à l'utilisation de la gite m, un asservissement de la finesse verticale et donc un asservissement de pilotage, vous permettant d'approcher au mieux le site d'arrivée de la capsule. Voir l'exposé théorique dans arc_atmo.htm

e) Vous tenterez une rentrée balistique ( f=0 ) sous un angle fort par exemple 15° et comparerez les résultats avec ceux simplifiés de la théorie d'ALLEN., notamment le niveau de la décélération maximum. Pour vous rapprocher des simplifications d'Allen, vous devrez annuler la gravitation ainsi que la rotation de la planète sur elle-même. Commentaires ?

f) Rien ne vous empêche, et ce serait intéressant, de tenter sur la fin de la rentrée ou même dès que possible, un freinage par parachutes. Pour ce faire, il faudrait alors vous renseigner sur les conditions de mise en œuvre des parachutes ( vitesse admissible, CX )

g) Un exposé succinct sur les rentrées avec vols humains serait le bienvenu et pourrait intéresser l'auditoire.

NB : Si un autre groupe traite cette même rentrée par la théorie de Chapman, comparez vos résultats et commentez.

DOCUMENTS FOURNIS : pouvant servir de confirmation lors de la mise au point des programmes.

Deux graphiques concernant une rentrée en atmosphère terrestre

V LA MISSION PATHINFINDER ( Lecture et travail ):

NB : Articles recopiés intégralement sur Internet

1°) LA SONDE ET LA MISSION :

Mars Pathfinder a été lancée le 3 décembre 1996 à 10h58, par une fusée Delta II 7925. Ce petit engin de 850 kg est parti avec un mois de retard sur la sonde Mars Global Surveyor, mais il est arrivé bien avant sa compagne, au terme d'un voyage de 7 mois. Le 4 juillet 1997 à 9h59 heure française, la sonde (qui ne pesait pas plus que 280 kg) s'est posée sur Mars, 20 ans après les atterrisseurs des sondes Viking ! La particularité de la mission Pathfinder, c'est que l'atterrissage n'a pas nécessité une mise en orbite autour de la planète (rentrée directe dans l'atmosphère). De plus, c'est la première fois qu'un robot se déplace sur la surface de Mars.

Le JPL sur le site de Pathdinder, donne les paramètres orbitaux du transfert héliocentrique:

a = 193216365 km

e = 0.236386

i = 0°.104

w = -9°.638

W = 81°.221

Puis le 1 mars 1997 à 0h ( JD = 2450508.5 ) les valeurs angulaires de position:

q = 85°.152 ou M = 58°807 et tp = 7566837.2 s :

2°) L'ATTERRISSAGE DE PATHFINDER :

L'approche finale a commencé par l'éjection de l'étage de croisière à 8500 km d'altitude, 35 minutes avant l'atterrissage. La capsule de descente, composé d'un bouclier thermique, de la sonde elle même et d'un bouclier arrière supportant le parachute et les rétrofusées entame sa chute vers la surface martienne. A 130 km d'altitude et 30 minutes plus tard, la vitesse de Pathfinder est de 7,5 km/s. C'est à ce moment que la sonde rentre véritablement dans l'atmosphère martienne. Son bouclier thermique de 2,65 mètres de long (hérité de Viking) la freine alors, tout en la protégeant d'un échauffement excessif. L'angle de rentrée est de -14,2°, et la vitesse tombe à 400 m/s. La sonde ralentit encore à 65 m/s lorsque le parachute s'ouvre deux à trois minutes après la rentrée dans l'atmosphère. Celui ci, d'un diamètre de 11,5 mètres, est éjecté par mortier alors que l'altitude n'est plus que de 9,4 km. Le bouclier thermique est lui même éjectée dix secondes plus tard, à 8,3 km de la surface. A 6,6 km, la sonde est larguée au bout d'un filin de kevlar de 30 mètres de long, fixé sur le bouclier arrière. Le radar altimétrique se met en marche et détecte le relief à 1500 mètres d'altitude. 8 secondes avant l'arrivée au sol, à 300 mètres d'altitude, une enveloppe protectrice composée de gros ballons (quatre grappes de six ballons chacune formant un tétraèdre de 5 mètres d'envergure) se gonfle autour de la sonde. Les trois rétrofusées à poudre s'allument à 50 mètres du sol, et la sonde semble pratiquement s'arrêter en plein ciel. A 15 mètres au-dessous du sol, le filin est coupé et la sonde termine sa descente vers Mars en chute libre, tandis que le bouclier arrière remonte vers le parachute sous l'impulsion des rétrofusées. Il s'agit d'entraîner celui ci le plus loin possible, pour éviter qu'il ne retombe sur la sonde. Pathfinder, protégée par ses "airbags", touche le sol. Elle va rebondir un certain nombre de fois avant de s'immobiliser définitivement. Les pétales s'entrouvrent, tandis que les ballons se dégonflent et sont tirés vers l'engin pour aller se loger sous les pétales. Un système particulièrement ingénieux permet à l'engin de se redresser s'il s'est immobilisé à l'envers. Il faudra trois quart d'heures aux ballons pour se rétracter complètement. La station est totalement déployée trois heures après. Sojourner est prêt à partir ...

QUESTION: What is the drag coefficient for the Mars Pathfinder's heat shield and parachute? How many G's will Pathfinder pull during entry? ANSWER from Robert Manning on July 2, 1997: The entry vehicle (at supersonic speeds) has a drag coefficient of about 2. At subsonic velocities whith the vehicle under, the the drag coefficient of the parachute is about 0.47. During atmospheric entry the peak deceleration may be as high as 20 Earth gees.

IV QUELQUES VERIFICATIONS NECESSAIRES :

On prend m_T=39.86 10 ¹³ m³s^-2, T_T=86164.1 s, w_T=2p/T_T

Le système différentiel du mouvement met en jeu:

La force de gravité G. Si elle est seule présente, l'intégration doit donner les conditions relatives d'un mouvement képlérien, on peut donc vérifier l'algorithme d'intégration et l'écriture correcte du système sur des cas simples, de complexité graduelle croissante .

ORBITE GEOSTATIONNAIRE Rx=RZ=0, ro=42164.157 km, Vo=0, go=0, Lo=0, lo=0, bo=90°, le système devrait fournir comme solution l'orbite géostationnaire en relatif: r=42164.157 km, V=0, g=0, L=0, l=0, b=90° aux erreurs d'arrondi près, c'est à dire un satellite équatorial, fixe au dessus du point de longitude L=0°.	CAS N°1
-------------------------------------------------------------------------------------------------------------------
ORBITE POLAIRE Rx=RZ=0, ro=7000 km, Vo=7528.7648 m/s (Pour une vitesse absolue de 7546.0491 m/s et une vitesse d'entraînement de 510.448 m/s), go=0, Lo=0, lo=0, bo=0°, le système devrait fournir comme solution une orbite circulaire polaire, avec en relatif: r=7000 km, V variable de 7528.7648 m/s à 7546.0491 m/s au dessus des pôles, g=0, L variable, l variable de -90° à +90°, b=0°, aux erreurs d'arrondi près. On devrait vérifier qu'à chaque période de 5828.5 s la longitude se décale d'une quantité constante vers l'ouest DL= 24°.352 à l'équateur	CAS N°2
-------------------------------------------------------------------------------------------------------------------
RETOMBEE D'ETAGE LANCEUR ( Exercice satellite n°6 du site ) Rx=RZ=0, ro=6438 km, Vo=2700 m/s, go=0°, Lo=0, lo=0, bo=90°, le système devrait fournir comme solution une trajectoire de retombée, en relatif: r variable de 60 km à un maximum de 86 km à l'apogée, avec une arrivée au sol vers 225 s, V, g variables, L variant de 0 à une longitude de 5°.26 pour le point de chute, correspondant à une distance sol d'environ 585.6 km, l=0, b=90° aux erreurs d'arrondi près. NB : Je vous incite à réaliser, dans le cadre de votre projet, une routine d'application qui pourrait visualiser la retombée d'un étage lanceur, après demande des paramètres de tir initiaux du lanceur au moment de la séparation.	CAS N°3
-------------------------------------------------------------------------------------------------------------------
POINTS SURVOLES = TRACE AU SOL Les équations fournissent après intégration, les variables géographiques locales L et l notamment, ce qui est excellent pour expliciter la trace au sol, connaissant les conditions relatives d'injection. Vous pouvez donc retrouver la trace sol d'un satellite de type MOLNYA( comme traité en exercice, sur ce site ) Rx=RZ=0, ro=6875 km ( périgée à 497 km du sol ), Vo=9822.5 m/s (Pour une vitesse absolue au périgée de 10047 m/s et une vitesse d'entraînement de 224.5 m/s), go=0, Lo=0 ( satellite dans Greenwich à t=0 s ), lo= - 63°4, bo=90°( Tir vers l'Est ), le système différentiel devrait fournir comme solution une orbite elliptique avec en relatif: r variant de 6875 à 46250 km,V variable de 9822.5 m/s à 1494 m/s L variable, l variable de -63°.40 à +63°.4, b variable, aux erreurs d'arrondi près. On devrait vérifier qu'à chaque période de 43082 s, une orbite phasée 2/1, et une trace au sol typique. NB : On peut donc suggérer de réaliser, dans le cadre de votre projet, une routine d'application qui tabule, puis visualise graphiquement la trace au sol, après demande des paramètres de tir initiaux Vo, ro, go=0, Lo=0, lo=0, bo=90°, accompagnés de to. La trace pourrait aussi être graduée en temps .	CAS N°4
-------------------------------------------------------------------------------------------------------------------
CONSEIL : Vous pourrez aussi valider votre projet, en comparant vos résultats avec ceux d'une rentrée terrestre équatoriale que vos camarades ont peut-être choisie.	CAS N°5

GUIZIOU Robert décembre 2002- complété novembre 2004 , sept 2011