RENTREE ATMOSPHERIQUE D'UN PLANEUR HYPERSONIQUE REVENANT DE LA LUNE

I PRESENTATION :

RAPPEL SUR APOLLO 11 :

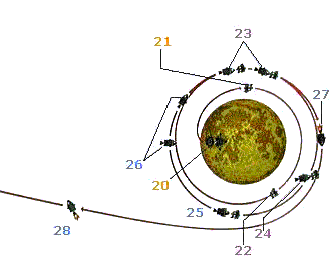
20, 21 : La mission achevée, la partie supérieure d’Eagle décolle et se place en orbite lunaire. 22, 23 : L’étage de remontée du LEM Eagle s’approche du CSM avec toujours Collins à son bord et s’y amarre. 24, 25 : Les trois astronautes se retrouvent dans la capsule Apollo (en fait le CSM), puis larguent le LEM qui s’écrase sur la Lune. 26, 27 : Le CSM passe sur une trajectoire de transfert terrestre, et son moteur principal est mis en route. 28 : Les astronautes procèdent à quelques corrections de trajectoire et sortent récupérer les films et photos pris par les caméras extérieures.

1°) Généralités :

On s'intéresse ici au problème du retour, sur une planète, d'un engin spatial, par une méthode passive où la dépense d'énergie est naturelle, sans intervention d'un moteur pour la partie principale du freinage. Classiquement, ces retours utilisent donc le freinage aérodynamique dans l'atmosphère de la planète.

On ne compte plus les retours atmosphériques vers la terre, qui sont devenus routiniers tels ceux de la navette US ou les équipages de la station MIR. D'autres restent historiques comme ceux de Gagarine ou de Glenn. Bientôt, probablement, cette technique sera utilisée, pour l'arrivée sur mars de futures explorations spatiales.

Le cas envisagé, dans ce projet est celui d'un retour après un voyage lunaire, du type rentrée de la capsule Apollo.

A partir de l'étude faite en cours du mouvement d'un lanceur, vous adapterez la théorie au cas de la rentrée d'un aéronef.

La recherche de documents devrait faire partie du projet, pour illustrer et conforter les résultats et aussi permettre une meilleure compréhension du phénomène ainsi qu'une analyse plus fine des éventuelles erreurs que vous pourriez commettre.

2°) Conditions de la rentrée:

Pour ce projet on se limitera à une rentrée plane, équatoriale, pour laquelle on pourra confondre vitesse relative et vitesse absolue, tellement la vitesse de rentrée est importante devant celle due à la rotation terrestre. A la limite, en complément de l'étude, vous pourriez supposer que la terre ne tourne pas ( w_T = 0 ) et comparer les résultats.

La rentrée est considérée comme effective à partir de l'altitude Z_E = 120 km du sol terrestre.

La cabine revient de la lune et possède donc une vitesse voisine de la vitesse de libération, nous prendrons donc une valeur de la vitesse d'entrée V_E = 11000 m/s.

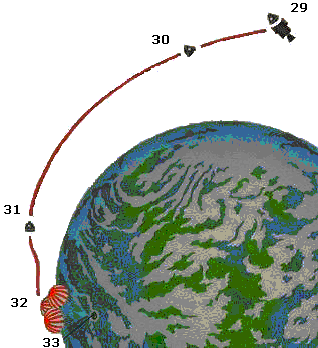
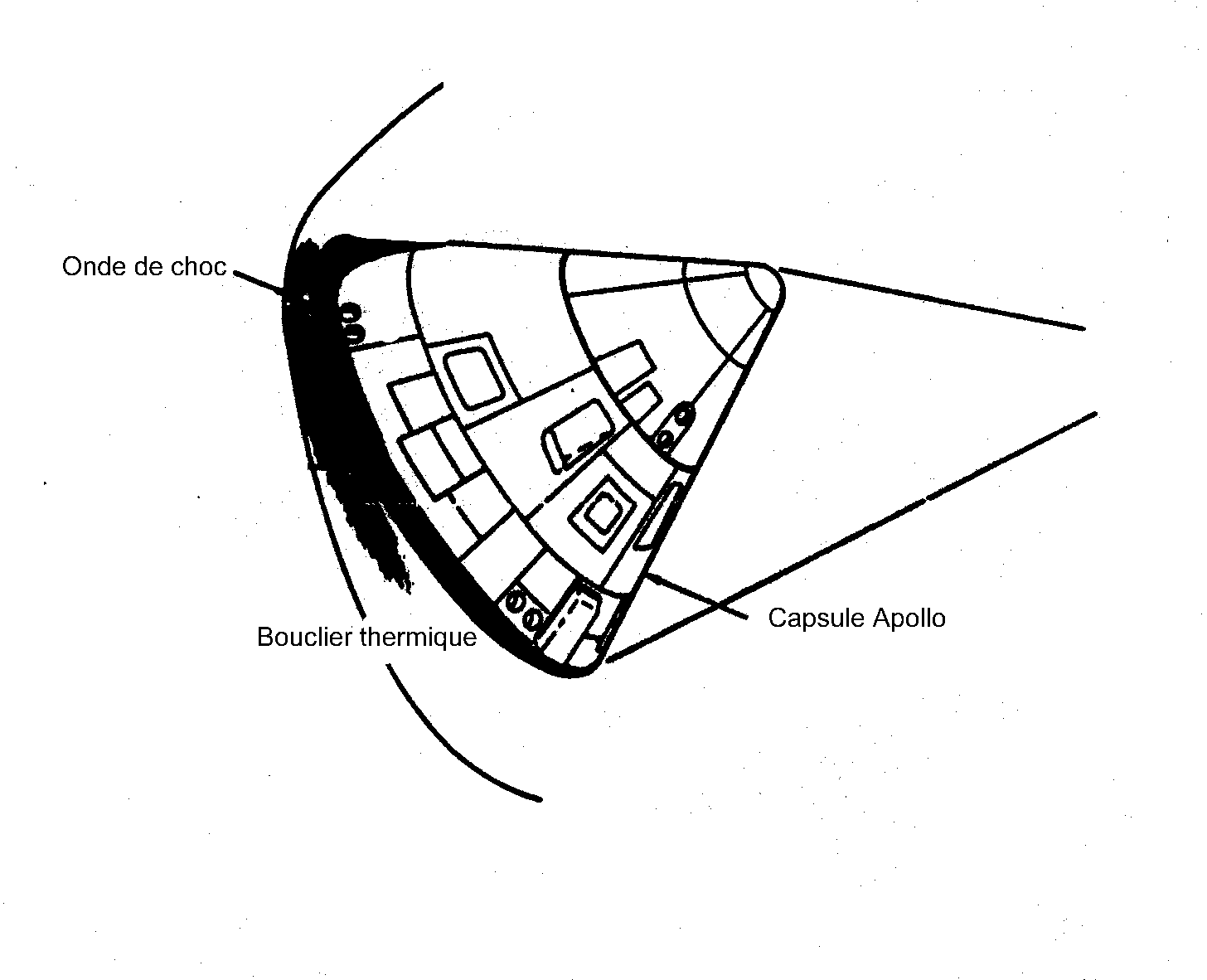
29, 30 : Largage du module de service SM et entrée du module de commande dans l’atmosphère. Le CM arrive à la vitesse de 11km/s et change d’orientation pour présenter son bouclier thermique en avant (la température extérieure atteindra 2600°C) et diminuer sa vitesse. 31 : Interruption des liaisons radio sous l’effet de la chaleur. 32, 33 : Freinage final à l’aide des parachutes puis amerrissage dans le Pacifique.

La fin du vol s'effectue avec l'ouverture de parachutes

II FIGURES ET TRAITEMENT DES EQUATIONS :

1°) SYSTEME DIFFERENTIEL DU MOUVEMENT :

Vous établirez ou adapterez les équations générales du mouvement d'un lanceur, avec les notations suivantes et un nombre minimum d'inconnues de 4:

V_R : Vitesse relative

b : Pente de la vitesse relative (positive sous l'horizontale). NB: dans le cours sur le lanceur le signe est inversé, ce qui est normal puisqu'un lanceur "grimpe" alors qu'une capsule en moyenne "descend", même s'il y a des rebonds.

Z : Altitude sol

X(t) : Distance horizontale parcourue depuis la verticale du point de rentrée.

Notant Y le vecteur de R⁴ de composantes VR , b , Z , X , il vient le système différentiel suivant, du premier ordre et de la forme générale:

En explicitant:

i est l'incidence (i>0 vol sur le ventre, i<0 vol sur le dos).

Ce sera un paramètre important à maîtriser, notamment pour arriver à maintenir la capsule dans l'atmosphère. Vous serez amenés à vous poser des problèmes de pilotage et à opérer des inversions de portance, une fois les problèmes de rebonds constatés.

Vous devrez aussi modéliser l'atmosphère standard:

r = rho(Z) Masse volumique de l'air à l'altitude Z, soit en recherchant des tables de données pour Z variant de O à 120 km, ou si vous programmez en Pascal, avec l'unité AIRSTAND, ou avec le tableau ci-après tiré d'une programmation et que vous pourrez adapter à votre usage.

BEGIN

if ((z>=0) and (z<17)) then rho=1.293*exp(-0.1202*z) else

if ((z>=17) and (z<22)) then rho=3.8923*exp(-0.185*z) else

if ((z>=22) and (z<25)) then rho=1.3553*exp(-0.13707*z) else

if ((z>=25) and (z<30)) then rho=2.11643*exp(-.15489*z) else

if ((z>=30) and (z<35)) then rho=3.51386*exp(-0.1718*z) else

if ((z>=35) and (z<40)) then rho=1.34076*exp(-.14426*z) else

if ((z>=40) and (z<45)) then rho=1.044633*exp(-.1380207*z) else

if ((z>=45) and (z<50)) then rho=0.69735*exp(-.12904*z) else

if ((z>=50) and (z<60)) then rho=0.6188*exp(-0.12664*z) else

if ((z>=60) and (z<70)) then rho=0.45374*exp(-0.12148*z) else

if ((z>=70) and (z<80)) then rho=5.14519*exp(-0.15616*z) else

if ((z>=80) and (z<100)) then rho=42.8456*exp(-0.18266*z) else

if ((z>=100) and (z<110)) then rho=100.01581*exp(-0.1913*z) else

if ((z>=110) and (z<120)) then rho=11.2811*exp(-0.16712*z-0.4772)

else rho=0;

END;

INTEGRATION NUMERIQUE : On pourra consulter les conseils à l'adresse suivante algorithmes

VALIDATION DE L'ALGORITHME D'INTEGRATION :

Comme les équations du système sont exactes, si vous supprimez l'atmosphère ( Cx = Cz = 0 ) et si vous "bloquez" la planète en rotation propre, alors vous avez un mouvement képlérien.

Donc ayant choisi, Vr, b, Z, vous calculez les constantes E et K puis a, e, ...le temps de vol depuis le point de départ, puis par les conservations de E et K, vous trouvez Ve vitesse d'arrivée sol, et la pente d'arrivée sol.

Le calcul "à la main" devrait recouper l'intégration avec une grande précision.

III DONNEES, CONDITIONS LIMITATIVES ET RESULTATS :

Pour la terre m_T = 39.86 104 km³s^-2 R_T = 6378 km

1°) Conditions de vol :

Vous adopterez les conditions de vol suivantes:

Z < 10 km Ouverture des parachutes, la théorie n'est plus applicable

Z > 120 km Entrée ou sortie de l'atmosphère ( rebonds éventuels après une trajectoire képlérienne ).

Vr < 640 m/s L'hypothèse de vol hypersonique avec des coefficients aérodynamiques constants n'est plus valable.

2°) Planeur utilisé :

M Masse du corps de rentrée

S Surface du maître couple

C_X Coefficient aérodynamique de traînée en hypersonique

C_Z Coefficient aérodynamique de portance

Pour Apollo Le facteur SC_X/M = 0.0032 m²kg^-1

f = CZ/CX Finesse aérodynamique

NB: 0< f < 0.35 la finesse peut varier grâce au pilotage.

V_E Vitesse absolue d'entrée dans l'atmosphère à 120 km 0 calculer

g_E = b_E angle de rentrée

3°) RESULTATS A FOURNIR :

Vous les présenterez soit en fonction de la variable de Chapman, soit en fonction du temps ou alors pour un profil de vol Z=Z(X) de l'altitude en fonction de la portée horizontale.

Vous commenterez abondamment avec des graphiques associés, le pilotage adopté dans les choix que vous aurez effectués.

a) VARIABLE DE CHAPMAN :

De nombreuses publications utilisent pour le tracé des courbes une variable u appelée variable de CHAPMAN ( chercheur qui s'est beaucoup intéressé aux problèmes de rentrée). Cette variable est sans dimension est le quotient de la vitesse absolue horizontale et de la vitesse absolue d'orbitation circulaire là où est la capsule.

Vous éviterez l'abus de tableaux de résultats , ceux que vous fournirez seront les plus significatifs et soigneusement annotés.

Vous étudierez en particulier:

L'influence de l'angle de rentrée sur la décélération maximum

o à finesse nulle et un angle de rentrée variant de 0 à 6°.

o à finesse non nulle entre 0 et 0.35 et un angle de rentrée fixé.

o L'influence de la finesse sur les profils Z = Z(u), pour divers cas de rentrée.

o La portée horizontale et l'influence des divers paramètres sur cette portée.

Vous commenterez les résultats et notamment les comparerez avec ceux que vous aurez pu trouver dans les documentations.

Un exposé sur les rentrées avec vols humains serait le bienvenu et intéresserait l'auditoire.

b) Quelques résultats:

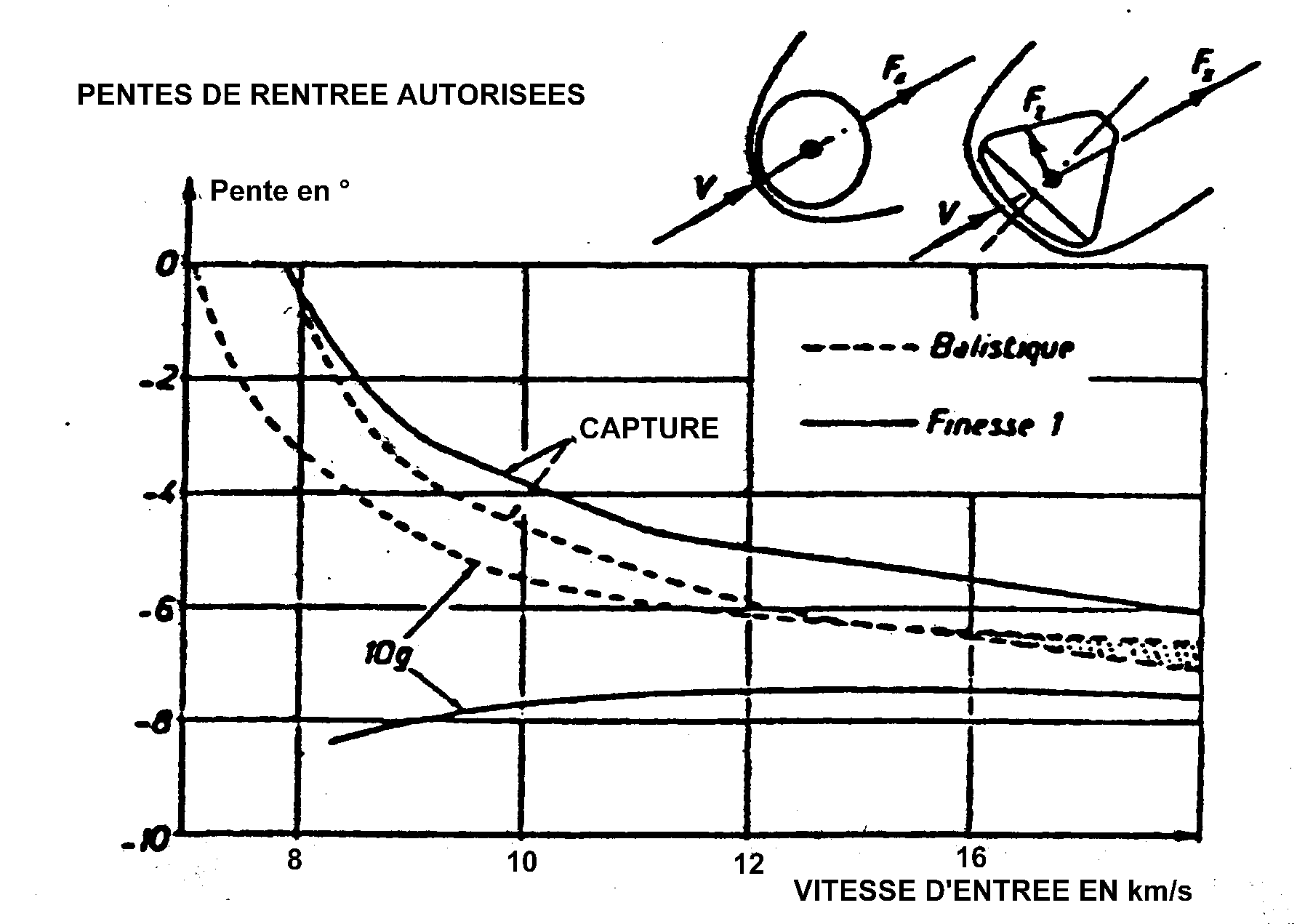
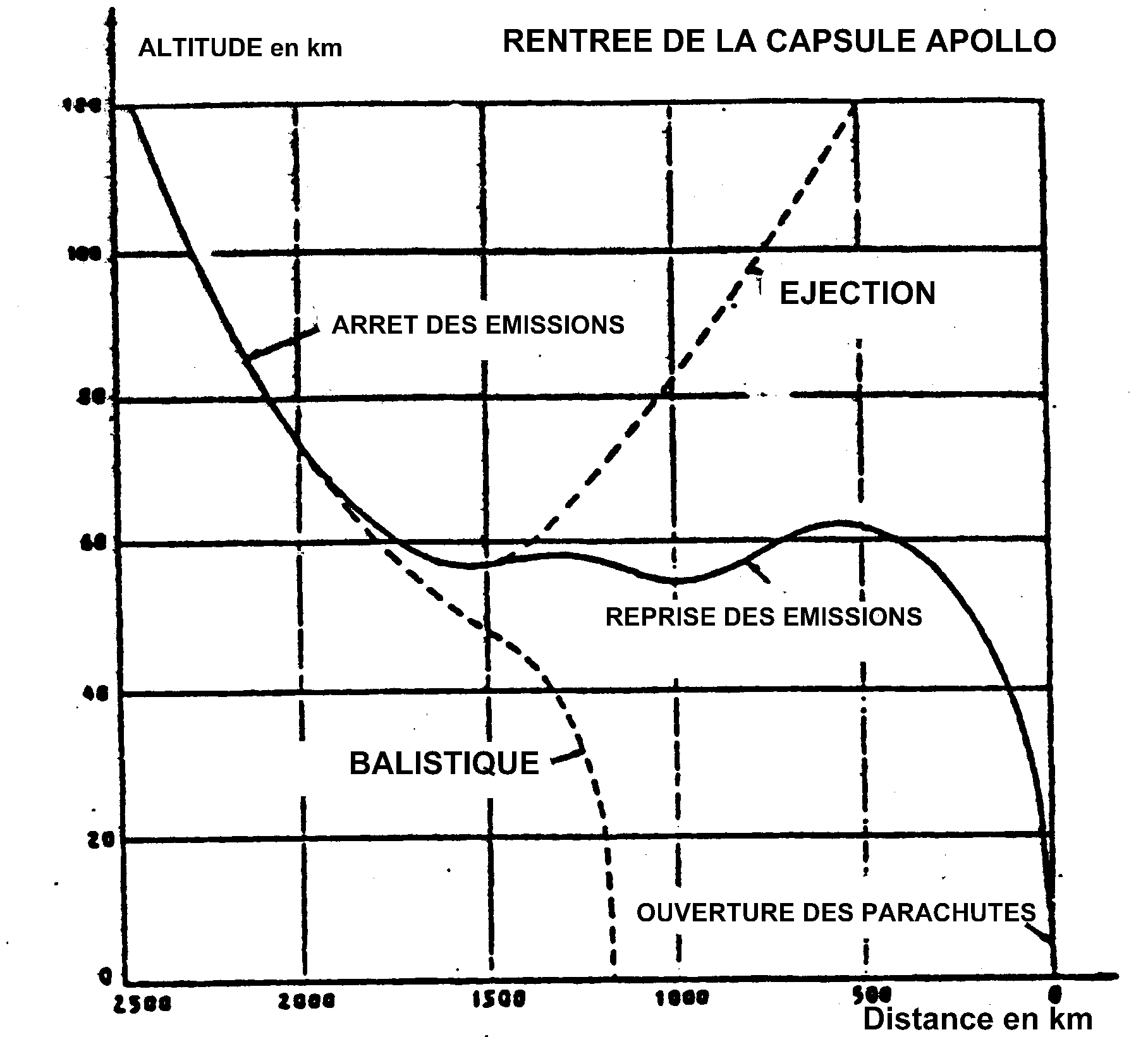
c) Notion de corridor de rentrée:

Vous vous renseignerez sur cette notion et essaierez de retrouver les résultats de la NASA pour la rentrée d'Apollo.

GUIZIOU Robert décembre 2002, sept 2011