Les USA ont en octobre 1989 lancé une sonde spatiale nommée Galiléo, destinée après un voyage très tourmenté et complexe, à atteindre la planète Jupiter pour l'étudier ainsi que ses satellites.

Galiléo emprunte une orbite héliocentrique C1 qui, partant de la Terre, survole la planète Vénus en y réalisant un premier tremplin gravifique le 9/02/1990 la sonde et renvoyée vers la Terre où elle effectue un second tremplin gravitationnel le 8 décembre 1990.

Nous nous intéressons à l'orbite C3 après le tremplin sur la Terre spécialement étudié pour amener Galileo à survoler à nouveau la Terre 2 ans après, afin d'y réaliser l'ultime tremplin et gain de vitesse, qui projettera la sonde vers sa planète de destination, Jupiter

NB: Les dates non calculées seront toujours prises à 0 H, car nous n'avons pas la prétention de calculer de telles missions à l'heure près.

NB 2 : Ce problème vous donnera l'occasion d'utiliser les routines du BDL( qui ne fonctionnent qu'en intranet ou si vous les téléchargez pour les exécuter chez vous)

Données utiles de ce vol:

( NB : Solution dans cette même page )

Sur Internet, vous devez télécharger la routine et ses ressources(voir plus haut) et l'exécuter ensuite.

Ceci, pour récupérer les coordonnées rectangulaires et la vitesse de la Terre le 8/12/1990 .

2°) A PROPOS DE GASPRA( Astéroïde N°951) :

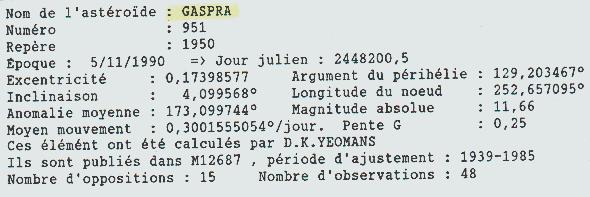
a) Quel est le demi grand axe de l'orbite de Gaspra?

3°) PROBLEME DE LAMBERT :

"Il n'existe qu'une seule conique képlérienne, joignant 2 points donnés du système solaire avec une durée de voyage imposée"

NB : CALCULEZ LA PERIODE SUR C3 ET COMPAREZ A CELLE DE LA TERRE ( 365.25 jours)?

Quelle est la vitesse à l'infini de Galileo à la sortie de la sphère d'influence de la Terre ?

Au passage près de Gaspra ?

 4°) SURVOL HYPERBOLIQUE DE LA TERRE LE 8/12/1990 :

Comparer les normes des vitesses à l'infini d'entrée et de sortie de la sphère d'influence de la Terre.

La documentation donne une altitude de survol au périgée de 1000 km. Calculer alors

a) Le demi angle d'ouverture des asymptotes de l'hyperbole.

 5°) SURVOL HYPERBOLIQUE DE LA TERRE LE 8/12/1992 :

Vous avez maintenant en main tous les outils de calcul et pourrez donc, le 8/012/1992, 2 ans après le précédent tremplin sur la Terre, calculer :

1°) Coordonnées rectangulaires et vitesse de la Terre le 8/12/1990.

Pour la Terre le 8/12/1990 on a :

2°) A PROPOS DE GASPRA( Astéroïde N°951) :

a) Quel est le demi grand axe de l'orbite de Gaspra?

Le moyen mouvement n permet de calculer la période et donc le demi grand axe de Gaspra.

Le BDL donne le moyen mouvement de Gaspra, n = 0.3001555054°/jour ====> Période T=1999.378 jours et un demi grand axe a(Gaspra) = 330.494 10⁶ km

b) Passage au périgée. Coordonnées héliocentriques le 29/10/1991 et distance au Soleil.

Le 5/11/90; le temps écoulé depuis le périgée est donné par la routine: 576.70021767 jours solaires moyens, ce qui place le périgée à la date julienne JJ = - 3921.20021767 soit 7 avril 1989 à 7 h 12 mn.

Depuis le passage au périgée jusqu'au 29/10/1991 il s'est écoulé 934.7002 jours. Ou bien on peut aussi calculer l'anomalie moyenne au 29/10/1991 alors qu'il s'est écoulé 358 jours depuis le .5/11/1990

M(29/10/1991) = 173°.099744+0.3001555054*358 = 280°.55541 Une nouvelle exécution de PAR_RV_S.EXE donne pour le 29/10/1990:

3°) DETERMINATION DE C3 :

a) Durée du voyage entre les 2 dates.

Avec datejuli.exe on trouve les dates juliennes:

JJ(8/12/1990)= - 3311.5 et JJ(29/10/1991)= -2986.5, ce qui donne une durée de voyage de 325 jours solaires moyens.

3°) Caractéristiques et paramètres orbitaux de C3.

a) L'exécution de LAMBERT1.EXE donne les résultats suivants :

Paramètres orbitaux :

REMARQUE CAPITALE : Les experts du JPL ont " parfaitement calculé leur coup " en effectuant un survol de la Terre diaboliquement précis pour imprimer à C3 une période de 731.8 jours, double de celle de la Terre, de manière à retrouver celle-ci exactement 2 ans après, pour un troisième et ultime tremplin.

b) Calculer la vitesse de Galileo soit au départ près de la Terre, soit à l'arrivée près de Vénus

On exécute 2 fois PAR_RV_S.EXE ce qui fournit confirmation des positions et apporte en plus les vitesses héliocentriques de Galileo.

 4°) SURVOL HYPERBOLIQUE DE LA TERRE LE 8/12/1990 :

Au passage près de Gaspra ?

On calcule par différence la vitesse relative de Galileo, par rapport à la planète Terre et on trouve :

Il peut se calculer de 2 manières:

1) Par les vitesses à l'infini :

 2) Par le périgée de l'hyperbole :

La vitesse à l'infini d'entrée, permet de calculer, par conservation de l'énergie, le demi grand axe de l'hyperbole :

NB : La petite différence tient à notre ignorance des corrections de trajectoire et aux simplifications d'usage et aussi à notre choix des dates à 0 h( une plus grande précision eut été ridicule face à l'hypothèse des sphères d'influence )

L'effet de tremplin remplace au moins 2 moteurs qu'il aurait fallu emporter pour réaliser la modification du vecteur vitesse héliocentrique entre l'arrivée et la sortie de la sphère d'influence de la Terre. Un tel tremplin est déjà relativement important. Une étude détaillée montrerait que le gain de vitesse en norme est sensible et que le tremplin a également servi à "faire tourner" le vecteur vitesse.

5°) SURVOL HYPERBOLIQUE DE LA TERRE LE 8/12/1992:

Coordonnées rectangulaires et vitesse de la Terre le 8/12/1992.

Naturellement ces valeurs sont très proches de celles du 8/12/1990

Vitesse de Galileo le 8/12/1992.

Du 8/12/1990 au 8/12/1992 il s'est écoulé 731 jours, l'anomalie moyenne sur l'orbite de Galileo vaut en radians:

M(8/12/1992) = 703°.19298 mod 360 = 343°.19298

PAR_RV_S.EXE donne alors une vitesse héliocentrique et une vitesse à l'infini d'arrivée:

NB : La vitesse à l'infini d'entrée dans la sphère d'influence de la Terre est de 9.342 km/s, un peu différente de celle que l'on trouvera en sortie, après le tremplin Terre et qui vaut 8.855 km/s. Normalement ces 2 valeurs sont très voisines. Alors où est le problème?

Réponse probable : le détour par Gaspra est certes intéressant, mais ne donne pas exactement une trajectoire qui rejoint parfaitement la Terre. Certes c'est très près, mais une petite correction de trajectoire a dû être nécessaire;

Si on recherche la trajectoire C3* qui joint Gaspra le 29/10/1991 à la Terre le 8/12/1992, on trouve avec DEUX_PTS.EXE :

Paramètres orbitaux de C3* :

Guiziou Robert février 2002