|
PILOTAGE 1-AXE PAR TUYERES |
![]()
![]()
Cet exercice illustre un
L'étude peut être abordée par toute personne ayant des rudiments d'automatique, université ou classes préparatoires.
PROBLEME
I DONNEES :
La commande peut tout aussi bien s'appliquer à un paramètre linéaire qu'à un angle. Ceci explique que par commodité d'écriture nous appelions le paramètre x et sa dérivée V. Il est vrai que pour un satellite c'est le plus souvent un angle
q et une vitesse angulaire dq/dt.Le paramètre à "surveiller" est donc un angle local d'attitude noté X, de vitesse angulaire notée V, qui doit rester nul en permanence. Cet angle évolue en continu sous l'effet d'un couple perturbateur autour de son axe de mesure, COUPLE SUPPOSE PETIT ET CONSTANT, noté Cp.
La commande fonctionne en tout ou rien et délivre un couple Cc de signe contraire à Cp. On notera
G l'accélération réelle pendant la commande.On désigne par :
|
I = 400 kg-m² |
L'inertie du satellite autour de l'axe de mesure de X |
|
Cp = 10-4 N-m |
La valeur du couple perturbateur, supposé >0. |
|
Cc = 0.4 N-m |
La norme constante du couple de commande, pouvant être >0 ou <0 |
|
G c ou Gp |
L'accélération angulaire du satellite, autour de l'axe de commande, pendant la commande ou la perturbation. |
|
Isp = 68 s = 680 m/s |
L'impulsion spécifique des ergols froids, utilisés par les tuyères. |
|
(D) X+KV=+S ( D) X+KV= -S |
Les équations, dans le plan de phase, 2 droites de commutation avec seuil S. |
|
K = 1 s |
Une constante associée à la commande |
|
T = 0.1 s |
Le retard de la commutation sur la commande |
|
S |
Le seuil à déterminer. |
II ETUDE GENERALE DE LA COMMUTATION AVEC RETARD :
L'étude se fait dans le plan de phase et l'état du système est repéré par le point M( X,V ). Entre 2 instants to et t1, le point M, entre les 2 droites D et
D, décrit un arc MoM1 sous l'action de la seule accélération perturbatrice Gp. En dehors des 2 droites le système est sous l'effet de la commande.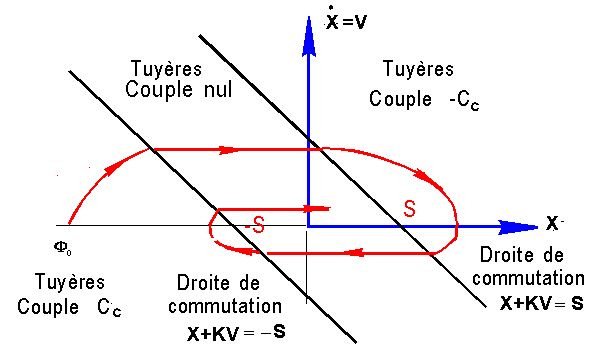
1°) Donner l'équation de la parabole MoM1. Donner les expressions de X et V en fonction du temps.
2°) INTRODUCTION DU RETARD T:
Classiquement lorsque le point M se trouve entre les 2 droites et atteint la droite de commutation D, le contrôle entre en action et impose une accélération
Gc< 0( On pourra alors négliger Gp devant Gc).Le système réel réagit avec un temps de retard T entre la détection et l'actuation. La commutation physique n'a lieu qu'en un point M2( X2, V2 ), différent de M1.
Calculer X2, V2 en fonction de X1, V1,
Gp, T. En déduire que tout se passe comme si la commutation était instantanée, mais sur une autre droite notée D1*, dont on donnera l'équation, et les constantes K* et S* associées.3°) EFFET DU RETARD SUR LA COMMANDE :
La commutation étant effectuée, la commande entre en jeu avec un couple
Gc<0. On peut alors négliger Gp devant Gc. Le point M suit un arc de parabole jusqu'à un point M3, point de commutation réelle, tenant compte lui aussi du retard T pris sur la commutation théorique se faisant sur D.Calculer comme précédemment l'équation de la nouvelle droite de commutation D2*, en précisant K2* et S2*.
4°) CYCLE LIMITE :
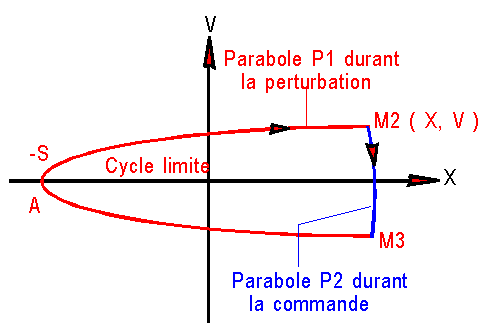
On souhaite montrer qu'un cycle limite optimisé, dans le plan de phase, est possible correspondant à la figure ci-dessus. L'optimisation porte sur la valeur extrême <0 qui vaut -S, de X sous l'effet pertubateur
a) Calculer la valeur de S en fonction de K, T,
Gp, Gc. Application numérique.Montrer que S vaut approximativement |
|
Vérifier littéralement puis numériquement que le temps de parcours sur la parabole (P2) de commande est pratiquement T.
b) Calculer la durée du trajet sur la parabole (P1). A.N
c) Le SCAO est constitué de tuyères 1 N. Calculer la consommation annuelle d'ergols. Calculer alors la consommation annuelle d'ergols froids du système de commande à tuyères.
![]()
![]()
Nous limitons les détails de la solution et ne donnons que les idées essentielles, laissant au lecteur le soin de compléter.
1°) PARABOLE MoM1:
C'est un mouvement à accélération constante qui donne :
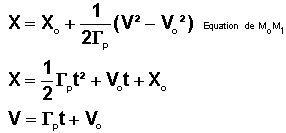
2°) CALCUL DE X2, V2 ET DE LA NOUVELLE COMMUTATION :
Il suffit de considérer que la perturbation est active de t1 à t1+T, et appliquer 1°) avec comme temps initial t1. Ainsi
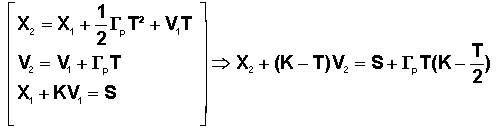
Telle est l'équation de la nouvelle droite de commutation D1*

3°) EFFET DU RETARD SUR LA COMMANDE :
Le calcul est strictement le même que précédemment en remplaçant
Gp par -Gc et donne une nouvelle droite de commutation parallèle à la précédente et vérifiant :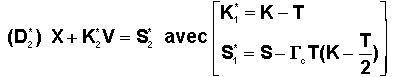
4°) CYCLE LIMITE :
a) CALCUL DE S :
L'existence du cycle limite repose sur 2 propriétés :
1 - Que les points de commutation virtuels sur D1* et D2* soient symétriques, on appelle (X,V) celui qui est sur D1*
2 - Que le sommet de la parabole décrite durant la perturbation se trouve en (-S, 0 )
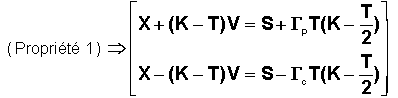
avec donc :

La propriété 2 est satisfaite en écrivant que la parabole de sommet A ( -S, 0 ) et d'équation V² = 2
Gp(X+S) passe par le point de coordonnées ci-dessus. Le calcul donne alors :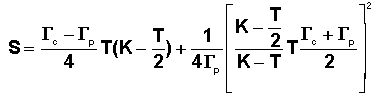
En remarquant que T<<K et
Gc/Gp = 4000, on a :
Conclusion : |
|
APPLICATION NUMERIQUE
:Avec les valeurs données, le lecteur vérifiera que :
K=1 s T=0.1 s Gp=2.5 10-7 N-m Gc=0.001 N-m |
|||||
S=2.8 10-3 rd |
Point M2 |
X=S=2.8 10-3 rd |
V=5.23 10-5 rd/s |
||
Temps de commande
:Sur ( P2) le temps Dt que dure la commande est égal à 2 fois celui qui mène de M2 à l'axe des X. Soit :
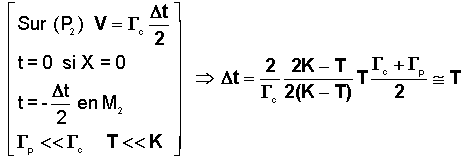
Le temps de commande est donc très court de l'ordre de 0.1 seconde.
b) TEMPS DE PARCOURS SUR (P1) :
Le lecteur, comme sur (P2) établira |
|
c) CONSOMMATION ANNUELLE :
Si
F est la poussée, q le débit massique et Isp l'impulsion spécifique, on connaît la relation F = q*Isp, donnant ici q=1.47 g/s.Le cycle perturbateur dure 420 s et celui de commande 0.1 s, donc le nombre de cycles par an est N pour une consommation d'ergols M :
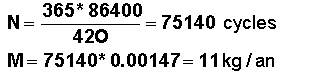
![]()
Guiziou Robert août 2000