TIR GEOSTATIONNAIRE RADOUGA

TIR GEOSTATIONNAIRE RADOUGA

NB : Nous avons choisi l'exemple, certes ancien, du premier envoi d'un géostationnaire soviétique, pour deux raisons:

1 - Les russes ont des lancements très difficiles et coûteux à partir de leurs bases de latitude élevée.

2 - Un article scientifique relate la mission, permettant de se familiariser avec la vulgarisation.

I ARTICLE A LIRE : DU MOLNYA AU RADOUGA ( Par Albert Ducrocq )

C'est en 1970 que l'on attend 'te premier satellite soviétique de communication en orbite géostationnaire auquel les Russes ont, par avance, donné le nom de Statsionar.

C'est seulement le 22 décembre 1975, à 20 h TU ( peu après minuit heure locale ), qu'est mise à feu la fusée porteuse de Statsionar-1, appelé Radouga (Arc-en-ciel).

Ce décalage de cinq ans a été motivé par un changement de politique, les Soviétiques s'étant employés, face à l'immense succès de l'organisation à domination américaine Intelsat, à produire un outil compétitif, à la fois dans l'espace et au sol.

Ainsi se sont-ils d'abord employés à créer l'instrument devant leur permettre, depuis leur territoire, d'atteindre de façon sûre et avec une grande précision un point déterminé de l'orbite géostationnaire. Leurs satellites de communication Molnya sont aujourd'hui lancés depuis Plesetsk avec utilisation de la plate-forme qui a été construite pour la R7 (fusée de Korolev) sur le cosmodrome nordique. Le Radouga est parti de Baïkonour avec utilisation de la fusée Proton, selon le processus suivant.

Dans un premier temps, le lanceur est utilisé à viser une orbite très basse, en I'occurrence une orbite quasi circulaire à 190 km, inclinée à 51°,5 sur l'équateur. Cette mission requiert le fonctionnement de deux étages, une différence importante entre la fusée Proton et la R-7 étant le fait que, dans cette dernière, le second étage est allumé dès le départ, alors que toute la partie inférieure de la fusée Proton est entièrement occupée par les moteurs RD-253, le second étage se trouvant au-dessus du faisceau constituant l'étage de la base . La fusée dans cette première prise ( liaison entre la Terre et une orbite basse ) opère pratiquement clé la même manière quelle que soit l'opération, cela expliquant que le complexe Proton de Baïkonour ait été utilisable sans modification pour mettre en place un satellite géostationnaire depuis leur territoire, les Soviétiques commencent par procéder selon le même scénario que pour le lancement d'un Saliout.

C'est dans l'espace que la situation change. La charge de la fusée est un véhicule, le "porte-Radouga", que trois modules constituent : un module de transfert, un module de circularisation, ou un module de communication ( ce dernier comprenant le satellite et ses systèmes de service ). Dès la satellisation assurée, ce véhicule prend son autonomie, l'étage supérieur de la fusée Proton étant abandonnée ,de sorte qu'il retombera au bout de trois jours.

51°,5 - 3° - 48°,5 =: 0

Quant au véhicule porte-Radouga, dont la masse est voisine de 19 t, il commence, lors d'un passage par l'équateur, par faire fonctionner son module de transfert selon technique rappelant étrangement l'élancement d'un Luna. Les méthodes, les moteurs, les techniques sont au demeurant les mêmes.

La manœuvre est cependant beaucoup plus délicate car il s'agit de faire d'une pierre deux coups, le transfert du véhicule sur une orbite de grand apogée devant être accompagnée d'une torsion de trajectoire.

Avant la mise à feu de son moteur, le véhicule soviétique commence ainsi par prendre une attitude qui placera L'axe de poussée dans une position faisant un angle de 12°,4 avec le vecteur vitesse. C'est alors une impulsion de 2503 m/s qui est créée. avec consommation de 10 t de combustible. Dans ces conditions la vitesse passe de 7 790 à 10 249 m/s, tandis que la torsion de l'orbite atteint 3°.

Le porte-Radouga se trouve, au terme de cette première manœuvre, transféré sur une orbite 340-35 850 km inclinée à 48°,5 et décrite en quelque 10 heures. Le module de transfert est alors largué, le véhicule se trouvant réduit à un engin à deux modules dont la masse ne, représente plus que quelque 7 t. Puis, lors d'un passage par l'apogée, le module de circularisation entre en service peu avant que l'équateur soit atteint pour créer une vitesse de 2349 m/s dans une direction faisant 79° avec la vitesse. Il en résulte une torsion de trajectoire qui atteint 48°,5, elle annule l'inclinaison de l'orbite et partant la nouvelle orbite est équatoriale. La manœuvre fait d'autre part passer la vitesse du véhicule de 1592 m/s à 3079 m/s, une telle valeur représentant, à 35850 km de la Terre, la vitesse circulaire. Autrement dit, la nouvelle orbite est quasi géostat0ionnaire,.on est assurément frappé, selon une telle technique par la disproportion des manœuvres ayant pour but une annulation de l'inclinaison de l'orbite. Les Soviétiques ont adopté la formule: 51°.5 - 3°.1 - 48°.5 = 0. Or le calcul nous apprend qu'une telle répartition est judicieuse. Nous savons en effet que les torsions de trajectoires sont très coûteuses lorsque les vitesses des engins sont grandes, autrement dit lorsque les manœuvres sont effectuées près de la Terre, ou du moins elles deviennent très coûteuses dès l'instant où elles sont importantes - à l'échelle de quelques degrés, le calcul apprend que la dépense est faible. Ainsi, sans torsion près de la Terre, la première manœuvre aurait requis une impulsion de 10249 - 7790 = 2459 m/s. Autrement dit, la torsion de 3° sur orbite basse n'exige que 44 m/s. C'est peu. En revanche,. ces 3° gagnés se révèlent précieux pour la correction équatoriale. Neutraliser 48°,5 coûte sensiblement moins que neutraliser 51°,5. Il y a donc une bonne optimisation des moyens.

ETUDE ET EXPLOITATION D'UNE REVUE DE VULGARISATION SCIENTIFIQUE

A partir de l'article relatant le premier lancement géostationnaire soviétique d'un satellite de télécommunications nommé RADOUGA, l'étude se propose de faire retrouver tous les résultats fournis.

La partie importante à lire de l'article est en gras

Règle du jeu : nous adoptons au départ les données de base de la mission, puisque c'est le choix des soviétiques.

Orbite d'attente (parking) : altitude quasi circulaire Z = 190 km et inclinaison de cette orbite initiale circulaire i = 51°5, décomposée plus tard en 3° et 48°,5

Orbite visée quasi circulaire finale d'altitude sol Z = 35850 km

Données numériques utiles :

Constante de gravitation de la Terre : m = 39,86 10⁴ km³ s^-2

Rayon terrestre équatorial R = 6378 km

Période sidérale de la Terre Tt = 86164,1 s = 23h 56mn 4,1 s

QUESTIONS

1° ) Illustrer par un dessin montrant la Terre le plan équatorial, l'orbite circulaire de parking, l'orbite elliptique de transfert, l'orbite géostationnaire, les étapes essentielles de la mission.

2° ) Calculer l'altitude d'orbitation circulaire géostationnaire dans l'hypothèse d'un potentiel newtonien. L'orbite définitive donnée dans l'article, l'est elle?

3° ) En fin d'exercice, reprendre le calcul de 2°), dans le cas où l'on tient compte de l'aplatissement de la Terre représenté par le terme J2 du développement du potentiel terrestre. VOIR SOLUTION

4° ) Supposant les incréments de vitesse délivrés en opérations de courtes durées ( donc approximation de l'altitude invariante ), calculer les éléments de la correction de trajectoire effectuée au périgée Vp, DVp.

L'angle y définissant l'orientation de l'axe de la poussée avec la vitesse avant allumage du moteur.

5° ) Il est annoncé un temps de montée d'environ 5 heures. Vérifiez.

6° a) Calculer comme en 4°) les éléments caractéristiques de la manœuvre à l'apogée , Va, DVa -

b) Le calcul montre une petite divergence avec l'article, notamment dans la vitesse d'orbitation circulaire. En fait, la vitesse de 3079 m/s fait passer le satellite sur une orbite de dérive dont on calculera l'apogée et la période avec exactitude.

Dans quel sens dérive RADOUGA, quelle est la dérive angulaire en degré/jour ? Dans quel but?

7° ) On peut se demander pourquoi, pour corriger 51°,5 les soviétiques ont choisi 3° et 48°,5 plutôt qu'une seule manœuvre à l'apogée. On choisira donc une correction x degrés au périgée et de 51°,5 - x degrés à l'apogée.

Exprimer la fonction f (x) = DVp(x) + DVa(x)

a) Montrer par une méthode de votre choix qu'une valeur de x voisine de x = 3° rend f(x) minimale, ce qui conduit naturellement à une consommation d'ergols minimale.

Quelle est la réserve de vitesse ainsi économisée par rapport à une seule manœuvre opérée à l'apogée ?

b) L'article indique que la masse de l'engin ( moteur + satellite ) est d'environ 7 tonnes. En donnant une estimation de l'impulsion spécifique des ergols Isp = 2900 m/s évaluer approximativement le gain de masse d'ergols ainsi réalisé.

c ) Vous comparez le coût total de la mission avec celui d'une mission identique à partir d'une orbite de parking équatoriale.

Fin du BE

ELEMENTS DE REPONSES

Nous donnons les figures, les grandes lignes de la solution sans entrer dans les détails des calculs.

1°) GEOMETRIE DE LA MISSION :

L'orbite finale visée est équatoriale, donc la dernière manœuvre doit être exécutée à un nœud de l'orbite de transfert de type GTO ( en orangé ), et si possible à l'apogée, où la vitesse orbitale est la plus faible.

Donc le périgée de l'orbite GTO doit être sur l'équateur, puisque l'apogée y est. Ceci impose donc, puisque le périgée est l'endroit de la manœuvre de périgée, qu'on attende que le lanceur sur son orbite de parking Co ( en rouge ) passe au dessus de l'équateur.

2°) Calcul classique à partir de la période, on trouve son rayon

r_g = 42164,16 km

3°) Comme la terre est renflée à l'équateur, l'attraction à l'équateur est plus forte, donc pour conserver la même période, il faut "poser" le géostationnaire un peu plus haut. Le calcul donne

( r_g)réel = 42164,7 km

4°)Eléments de la correction de trajectoire effectuée au périgée Vp, DVp, y.

Une figure est nécessaire du triangle des vitesses au périgée.

Le moteur de périgée réalise deux opérations en une seule manœuvre :

1 - Atteindre la vitesse Vp au périgée du transfert quasi GTO

2 - Réaliser une "torsion" de trajectoire, ou encore rectifier l'inclinaison de 3°.

Les calculs sont simples, Vo est la vitesse d'orbitation circulaire à 190 km du sol Vo = 7790.3 m/s

Vp est la vitesse au périgée d'une orbite dont on connaît le périgée 190 km sol et l'apogée 35850 km sol, avec 2a et la conservation de l'énergie, il vient Vp = 10248.8 m/s.

L'incrément de vitesse DVp se calcule dans le triangle des vitesses et vaut Vp = 2502.6 m/s

Le lanceur doit s'orienter dans une direction précise faisant l'angle y = 12°4 avec la vitesse Vo. Ce calcul est simple avec la relation des sinus dans le triangle des vitesses.

5°) Temps de montée d'environ 5 heures :

Le demi grand axe de l'orbite de montée vaut a = 24396 km, donnant une période de 37926 s et un temps de montée (demi période ) de 18963 s soit 5 heures 16 mn.

6° a) Eléments caractéristiques de la manœuvre à l'apogée :

A l'apogée la loi des aires ou la conservation de l'énergie sur la trajectoire de montée, donnent la vitesse au passage à l'apogée : Va = 1594 m/s

La vitesse d'orbitation circulaire à 35850 km du sol vaut Vg = 3072.3 m/s

Un nouveau triangle de vitesses est nécessaire avec l'ultime correction de 48°5 qui reste à faire, suivant la figure suivante :

Comme au périgée, les calculs donnent y = 79°13 m/s et Dva = 2343 m/s

7°) Orbite de dérive :

Il est vrai que l'article donne une vitesse de 3079 m/s, donc arrivé à l'apogée, cette vitesse ne peut conduire qu'à une orbite elliptique.

L'énergie vaut :

Cette dérive se fait vers l'Ouest, probablement dans le but de se rapprocher au mieux du point de stationnement définitif du géostationnaire. Ce point n'a pas été donné dans l'article.

7° ) a) Pourquoi 3° et 48°,5 plutôt qu'une seule manœuvre à l'apogée :.

Exprimons la fonction f (x) = DVp(x) + DVa(x)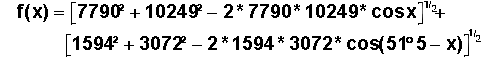

Le graphe présente l'allure suivante

Un "zoom" sur la zone du minimum donne :

montrant que le minimum a lieu pour sensiblement 3°, disons 2°.8, qu'il vaut 4846 m/s ( à comparer à 4884 m/s) et que par rapport à une manœuvre complète de 51°5 à l'apogée , le gain est de 38 m/s. Ceci peut paraître faible, mais dans le spatial, il faut savoir que tout gain de vitesse se traduit par un gain de masse utile. L'opération des ruses étaient donc parfaitement justifiée même s'il fallait deux orientations dans l'espace.

b) Gain de masse utile :

Le cours sur les lanceurs donne :

gain loin d'être négligeable.

Guiziou novembre 1999