|
CONTENU : Mis à jour
septembre 2007, revu sept 2011 I Orbite géostationnaire | Orbite géosynchrone Orbite géostationnaire képlérienne Orbite géostationnaire réelle | Intérêt Calcul de l'orientation d'une antenne Orbite GTO | Manœuvres de mise à poste Contraintes solaires | Contraintes de visibilité Créneau de tir | Bases non équatoriales |
|
Cette partie concerne une
application très importante, celle des satellites géostationnaires avec:
o
La
caractérisation de l'orbite dite géostationnaire et son intérêt.
o
Le
lancement GTO
o
Quelques
éléments de la mise à poste
o
Les
perturbations qui affectent le satellite
o
Le
principe de la maintenance à poste.
Les
télécommunications ont envahi notre monde moderne, et la nécessité de disposer
de satellites fixes par rapport à la terre, s'est rapidement imposée. En effet,
un tel satellite joue le rôle de relais de transmission ou d'un œil pour la
surveillance globale de la terre. Nous allons vérifier que ce type
d'application est possible.
On
appelle ainsi une orbite de période identique à celle de la terre, soit T=23 h 56 mn 4.1 s = 86164.1 s
En
hypothèse képlérienne, le demi grand axe est donné par:
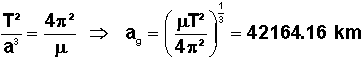
Une
telle orbite possède la propriété de survoler un même lieu géographique, à
chaque période, puisque la terre et le satellite auront tous les deux effectué
un tour complet et retrouvé la même position par rapport aux étoiles, mais avec
l'inconvénient de ne pas rester à la verticale d'aucun point de la terre..
2°) Orbite géostationnaire
képlérienne :
Si
on impose en plus à ce satellite de rester fixe par rapport à un point de la
terre, alors :
Ce
point ne peut être que sur l'équateur, sinon le satellite serait à la fois au
nord et au sud de l'équateur.
L'orbite
est nécessairement équatoriale
L'orbite
est obligatoirement circulaire pour éviter une oscillation Est-Ouest par
rapport.
Il
n'existe donc qu'une seule orbite satisfaisant à ces critères :
ORBITE CIRCULAIRE
EQUATORIALE DE RAYON Rg = 42164.16 km EN KEPLERIEN.
REMARQUE
:Classiquement, on rencontrera dans la littérature, qu'un tel satellite gravite
à 36000 km du sol. C'est en réalité la valeur arrondie correspond à une
altitude réelle képlérienne de 35786.16 km.
3°) Orbite géostationnaire réelle
:
Nous
savons que la terre est en première approximation assimilable à un ellipsoïde.
Le renflement équatorial terrestre crée donc un supplément d'attraction qui
accélère la vitesse. Pour que le satellite retrouve la bonne vitesse angulaire
ou linéaire, donnant la période sidérale, il faut le placer un peu plus haut.
Le calcul, que vous trouverez dans les exercices, donne en ne prenant pas en
compte les autres perturbations, une ALTITUDE GEOSTATIONNAIRE
VRAIE DE 42164.68 KM.
4°) Intérêt de l'orbite
géostationnaire réelle
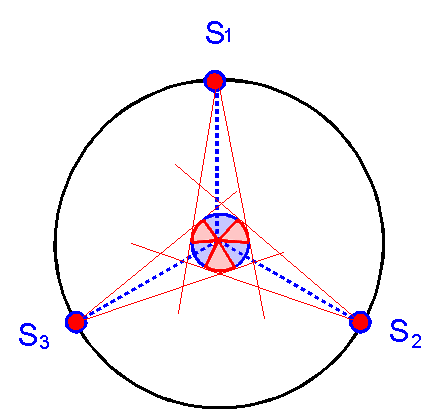
Le
dessin ci-dessus montre clairement, que trois satellites disposés à 120° sur
l'orbite géostationnaire, permettent "de voir" quasiment toute la
terre, à part une petite zone polaire située aux des extrêmes.
Les
zones en rouge sont voient simultanément deux satellites alors que les bleues
n'en voient qu'un seul. En utilisant deux satellites on peut communiquer d'un
point quelconque de la terre à un autre sans problème.
Seules
les latitudes au dessus de 81° environ ne sont pas accessibles.
Un
satellite en orbite géostationnaire est caractérisé par sa LONGITUDE DE STATIONNEMENT lS. Cette donnée
est capitale pour la réception des émissions par une antenne satellite, car
elle conditionne l'orientation en azimut et en déclinaison locale de l'axe de
l'antenne.
La longitude de stationnement est surveillée à 0.1° près.
EXEMPLES POUR LES SATELLITES EUROPEENS:
Actuellement
en 1998, les principaux satellites utilisés en France sont :
ASTRA à
19°.2 EST
EUTELSAT
II-F3 à 16°EST
EUTELSAT
II-F1 et HOT BIRD 1 -> 3 à 13° EST
TELECOM
2B/2D à 5° OUEST
TELECOM
2A à 8° OUEST
1°) Calcul de l'orientation de l'antenne :
La
réception correcte d'une émission satellite consiste à orienter l'axe de la
parabole de réception vers le satellite. Ce qui demande la connaissance de :
·
La
longitude de stationnement lS
·
Les
coordonnées géographiques longitude L et latitude l du lieu de réception
On
peut alors calculer par des considérations géométriques simples, dans le repère
géographique local: l'azimut géographique Az mesuré positivement vers
l'est et l'élévation El, qui est l'inclinaison sur le plan horizontal
local de l'axe de l'antenne.
Vous
trouverez dans la rubrique téléchargement une routine ANTENNE.EXE et son programme source ANTENNE.PAS
en Pascal, permettant ce calcul. NB : L'ensemble est regroupé dans antenne.zip.
Ceci
ne vous empêche pas de confirmer les résultats à la main. Si le repérage est
magnétique, il faut de plus connaître la déclinaison magnétique locale.
Peut
être avez-vous oublié la propriété géométrique d'un miroir parabolique : celle
de réfléchir tous les rayons lumineux, parallèles à l'axe de la parabole, vers
un point remarquable qu'on appelle le foyer. Cette propriété est utilisée dans
les télescopes pour concentrer soit des rayons lumineux, soit des ondes de
nature diverse.
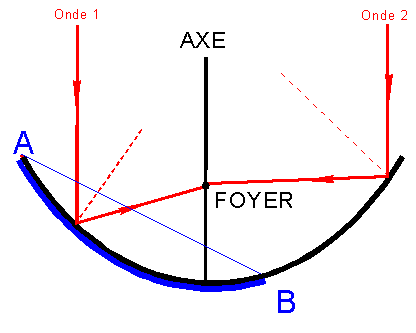
Naturellement
la tête de réception est placée au foyer. Pour éviter en pratique qu'elle ne
fasse ombre sur le miroir, on "taille" la parabole de manière non symétrique
de façon à placer la tête réceptrice hors du faisceau des ondes. C'est donc la
partie bleue AB qui est montée comme antenne, ce qui a comme autre avantage de
donner l'illusion que l'axe antenne est moins incliné, en général on gagne 25°
d'inclinaison.
III LANCEMENT GEOSTATIONNAIRE:
Nous
allons voir que rejoindre le point de stationnement n'est une affaire simple.
Il n'est pas question ici, de détailler à l'extrême toutes les opérations, mais
simplement de sensibiliser le lecteur aux principales étapes simplifiées pour
une meilleure compréhension.
1°) BASE DE LANCEMENT EQUATORIALE
:
C'est
le cas idéal, pour diverses raisons évidentes :
·
L'orbite
géostationnaire est équatoriale, donc un départ coplanaire à cette orbite évite
les corrections d'inclinaison orbitale.
·
Le
gain de vitesse dû à la rotation terrestre est maximal dans le plan équatorial,
pour un tir vers l'EST. La base de KOUROU avec une latitude de 5° est de ce
point de vue excellente.
·
On
peut éviter une mise en orbite d'attente quasi circulaire et injecter la charge
utile directement en orbite GTO ( GEOSTATIONNARY
TRANSFER ORBIT )
·
Cette
procédure qui consiste à "grimper" jusqu'au niveau géostationnaire,
présente l'avantage de n'utiliser qu'un seul moteur pour une correction
d'apogée, alors qu'un parking intermédiaire demande deux incréments de vitesse
et donc deux allumages de moteurs différents, car ces incréments ne sont pas
négligeables.
REMARQUES
: Un tir effectué par le Lanceur Ariane, qui effectue une injection directe sur
l'orbite GTO, ne demandera au satellite qu'un seul moteur d'apogée. Par contre,
la navette américaine réalise une mise en orbite de "parking" vers
280 km du sol, et impose donc à la charge utile ainsi satellisée d'être pourvue
de 2 moteurs:
o
Un moteur d'apogée qui
placera le satellite sur l'orbite GTO.
o
Un moteur d'apogée qui
réalisera les mises en orbite de dérive et la mise à poste définitive.
La
manœuvre est donc plus délicate et moins sûre, puisque demandant un allumage
moteur supplémentaire.
Détaillons
ces calculs élémentaires, donnant des ordres de grandeur, reposant sur un
transfert de type Hohmann, entre une injection au périgée bas, vers 200 km du
sol et une position haute, vers 42164 km du centre terre.
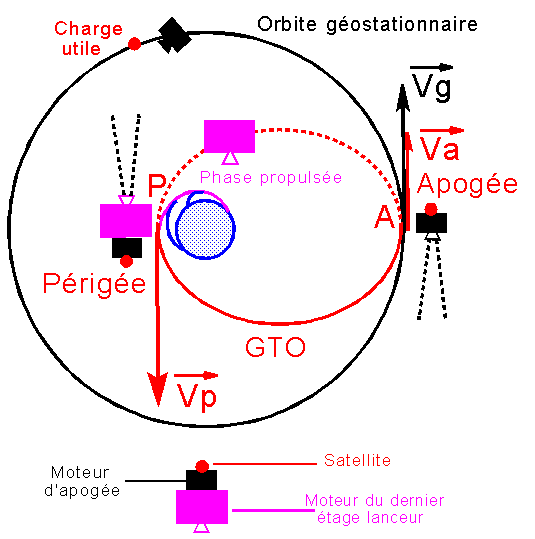
Le
lancement consiste, grâce à une phase propulsée, utilisant en pratique trois
étages d'un lanceur, à injecter au périgée P d'une orbite GTO une masse qui
comprend : Le moteur du dernier étage (en rose) accompagné d'un moteur
inutilisé (en noir) et de la charge utile proprement dite (le point rouge).
Cet
ensemble est satellisé à une vitesse Vp que l'on calcule sur l'orbite GTO:
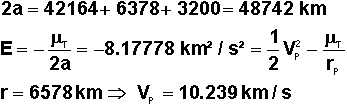
Si
l'on se souvient que la première vitesse cosmique pour rester en circulaire est
de 7.784 km/s à 200 km du sol, on réalise que la vitesse Vp=10.240 km/s est un
exploit, ce qui explique que l'on ait attendu avant de lancer des
géostationnaires.
Nous
sommes maintenant sur l'orbite GTO, pour laquelle le lecteur se convaincra, en
calculant la période qu'on parvient à l'apogée après 5 h 15 mn 32 s de vol.
Cette phase de montée a permis d'affiner les paramètres de l'orbite GTO, de
définir l'orientation précise de la poussée d'apogée, d'orienter le moteur
d'apogée après s'être débarrassé du troisième étage lanceur. Celui-ci va rester
sur l'orbite GTO un certain temps, pendant lequel la traînée au périgée usera
l'orbite, le satellite spiralant sur une trajectoire de moins en moins
excentrique, jusqu'à ce que, le périgée descendant, une rentrée atmosphérique
se produise. L'ensemble finit alors par brûler complètement dans l'atmosphère.
3°) MANŒUVRES DE MISE A POSTE:
Il
ne faut pas perdre de vue, que le but est de placer à une longitude imposée, un
satellite qui doit rester fixe par rapport à la terre.
De
toute évidence, comme le satellite repasse toujours par le lieu où une
correction de trajectoire est réalisée, lorsque le géostationnaire est à poste,
obligatoirement la dernière correction a lieu à cet endroit. Toutes les orbites
ont en commun la propriété d'avoir le grand axe comme ligne des nœuds, de manière à avoir l'apogée sur l'équateur terrestre.
Ainsi en général l'argument nodal w du périgée vaut w= 180°, c'est le cas des lancements
Ariane.
Il
faut donc qu'une orbite intermédiaire passe à l'apogée
par le point de stationnement. Il n'y a pratiquement aucune chance pour
que l'apogée de l'orbite GTO passe par le stationnement, même après plusieurs
orbites GTO consécutives. En effet, depuis Kourou, le périgée est toujours au
même endroit sur l'équateur, parce que la phase propulsée est verrouillée. Le
temps de montée (demi-période) est également toujours le même, donc le premier
apogée est sensiblement toujours au même endroit par rapport à la terre, et
cette position n'a aucune raison d'être le stationnement.
Nous
donnons dans la suite une procédure de principe idéale.
a.
Orbites
GTO primaires :
En
pratique, on laisse parcourir un certain nombre N1 de fois, pas plus de 10,
l'orbite GTO, jusqu'à UN APOGEE PROCHE DU STATIONNEMENT.
Un écart DL=Ls -La entre
le stationnement et l'apogée existe, de quelques degrés.
b) Orbites de dérives :
Le
principe est maintenant de passer sur une orbite très proche de l'orbite
géostationnaire, telle que parcourue N2 fois, le dernier apogée soit exactement
au point de stationnement. Un incrément de vitesse DV1 est nécessaire.
Cette
orbite de dérive CD1 est donc ajustée avec le plus grand soin.
REMARQUE :
Les corrections ne pouvant pas être parfaites, on conçoit qu'en réalité, il
faille des orbites de dérive plus nombreuses, permettant de réduire avec
précision l'écart en longitude.
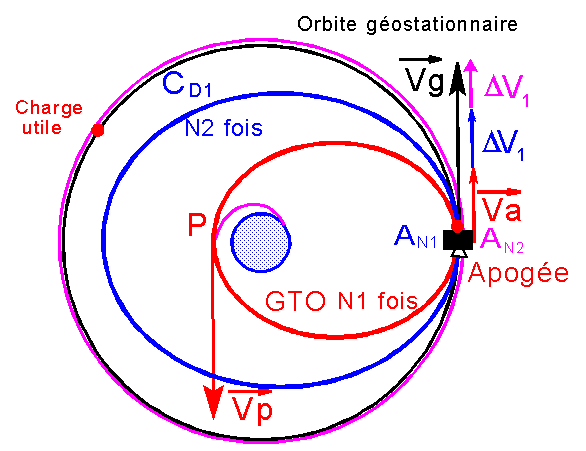
c.
Manœuvre
de circularisation :
Une
ultime manœuvre dite de circularisation, permet à l'apogée, grâce à un nouvel
incrément de vitesse DV2, de fixer définitivement le
satellite sur son poste. La mise à poste est achevée.
Commencera maintenant la maintenance à poste.
d.
Coût
en vitesse :
Dans
ce cas simple, la motorisation devra en tout délivrer un incrément total de
vitesse DV donné par :
0
|
Au
total en km/s, il vient |
|
On
remarquera que la vitesse de libération requise pour entrer dans le système
solaire, n'est que de 11 km/s environ à 200 km du sol. Donc la mise en
géostationnaire d'une masse donnée coûte plus cher qu'un envoi en libération. Il
suffit de rappeler qu'avec 11.5 km/s on atteint Mars ou Vénus.
Sans
entrer dans trop de détails, donnons quelques idées sur la mise à poste réelle.
Lors
de l'analyse de mission, il n'y a pas que l'aspect trajectoire qui soit
important.
Le
satellite demande une certaine autonomie et donc une puissance électrique
minimale. Donc la direction du soleil est capitale, en particulier l'ANGLE AXE
SATELLITE-DIRECTION DU SOLEIL qu'on appelle ANGLE
D'ASPECT SOLAIRE.
De
plus le soleil intervient dans les problèmes thermiques,
et enfin dans la détermination de l'attitude, à
l'aide de senseurs solaires en particulier.
Le
mouvement orbital sur les orbites GTO ou de dérives, entraîne des périodes d'éclipses solaires, durant lesquelles les
références solaires n'étant pas disponibles, les manœuvres sont interdites. Le
maximum de durée est autour des équinoxes,
avec un maximum de l'ordre de 70 mn/jour. La période d'éclipse dure 42 jours en continu.
Les
télécommunications Station sol - Satellite, notamment en phase de restitution
d'orbite, ne doivent pas être parasitée par les émissions électromagnétiques du
soleil. Il faut donc pendant es phases prendre une certaine sécurité par
rapport à l'alignement Terre-Satellite-Soleil.
Enfin
au coucher et au lever du soleil, des perturbations de transmission sont à
craindre, ainsi qu'un aveuglement des senseurs terre.
2°) Contraintes de visibilité :
Le
vol lanceur, puis le satellite, sont suivis à partir de stations sol.
Quelquefois dans certaines opérations deux stations doivent "voir" le
satellite avec un angle minimal sur l'horizon et une durée minimale imposée.
De
plus, même si le satellite est visible d'une station, il se pourrait que son
attitude (orientation spatiale), ne permette pas une liaison correcte.
L'ensemble
des remarques et contraintes ci-dessus et bien d'autres non soulevées, font que
l'analyse de mission doit définir les créneaux de tir acceptables et indiquer
leur répartition dans l'année pour tel ou tel lancement.
4°) Problème des bases non
équatoriales :
a.
Kourou : pour les tirs Ariane, notre base
de Guyane conduit à des injections au voisinage de l'équateur, avec une
inclinaison orbitale de l'ordre de 7°, qu'il faudra corriger, naturellement à
un nœud de l'orbite (ici périgée ou apogée) et nous savons que l'optimisation
impose l'apogée. La correction d'inclinaison conduit à un supplément de coût
propulsif.
b.
Bases
URSS : le problème
est plus important, car après un tir vers l'EST, qui conduit à une inclinaison
égale à la latitude de la base de tir, une orbite de parking circulaire
obligatoire. L'inclinaison de l'orbite d'attente basse est de l'ordre de 45°-
55°, c'est à dire très forte.
L'optimisation
de la mise à poste conduira à effectuer une petite correction au survol d'un
nœud, celui-ci devenant périgée de l'orbite GTO, et à achever la plus grosse
partie de la correction d'inclinaison à l'apogée où la vitesse est plus petite
qu'au périgée. Voir exercice RADOUGA.
5°) Perturbations :
On
peut constater qu'une mise à poste d'un géostationnaire, peut prendre deux à
quatre semaines. Durant cette période les perturbations orbitales font leur
effet. Il faut donc penser les manœuvres en fonction de ces perturbations et
faire en sorte qu'elles agissent de manière favorable pour économiser du
carburant et ainsi augmenter la durée de vie du satellite opérationnel.
En
particulier, il faut éviter de rester trop longtemps sur des orbites
intermédiaires de bas périgée, fortement affectées par la perturbation
luni-solaire.
Le
problème complet prenant en compte toutes les remarques précédentes, demande
une ETUDE D'OPTIMISATION.
On
appelle ainsi l'ensemble des opérations consistant à maintenir les paramètres
orbitaux du satellite dans un intervalle acceptable pour la mission.
1°) Notion de fenêtre de position :
Un
satellite géostationnaire est défini par sa longitude de stationnement. Sous
l'effet de perturbations diverses, son orbite, initialement circulaire et
équatoriale, de période T = 86164 secondes, va évoluer.
·
Le
satellite va donc quitter le plan équatorial, c'est le décalage Nord-Sud (
inclinaison perturbée ).
·
Le
satellite change de grand axe, donc de période, son orbite devient légèrement
excentrique, et donc le satellite se décale en Est-Ouest.
On
fixe donc des bornes en Longitude et en latitude, centrées sur le point de stationnement.
Ce patit domaine dans lequel il faut maintenir le satellite, durant sa durée de
vie, s'appelle la FENETRE DE MAINTIEN A POSTE,
une tolérance de 0.1 degré est acceptée.
2°) Maintenance et contraintes
:
Pour
rétablir les paramètres orbitaux du satellite, des manœuvres sont prévues, soit
commandées du sol soit gérées par l'ordinateur de bord.
Une
manœuvre est caractérisée par un INCREMENT DE VITESSE DV:
o De module si possible MINIMAL
o D'orientation connue
o A délivrer à une date bien
déterminée correspondant à une position précise sur orbite
Une
manœuvre devra être définie :
o Compatible avec les caractéristiques
des actuateurs: moteurs à gaz chauds, tuyères à gaz froids
o Tenant compte de l'évolution
naturelle de l'orbite, car certains paramètres dérivent toujours dans le même
sens, donc on cherche à les ramener du côté de la fenêtre où ils évolueront
vers le centre.
o En fonction de la date et de la
durée de la manœuvre ( problèmes de senseurs solaire ou terrestre, éclipses,
angle d'aspect solaire )
Compte
tenu de la manœuvre et des contraintes à respecter, le problème se ramène à une
MINIMISATION SOUS CONTRAINTES. En général ce n'est pas simple. La solution est
rarement totalement optimale et des simplifications sont tolérées. De même une
correction est rarement effectuée en une seule fois. Une stratégie tenant
compte des dispersions doit être mise en œuvre pour prendre en compte les
incertitudes des systèmes physiques.
Techniquement,
parce que les équations le permettent, on DECOUPLE les mouvements EST-OUEST et
NORD-SUD.
On
exerce alors :
o
Des
poussées tangentielles pour la correction de longitude
o
Des
poussées normales au plan orbital pour des corrections nord-sud.
Seules
les imperfections d'alignement des poussées vont créer de petits couplages
entre ces mouvements.
La
stratégie ignore aussi les effets perturbateurs périodiques qui ne font pas
sortir le satellite de sa fenêtre.
4°) Coût du maintien à poste :
La
surveillance LONGITUDE - DERIVE EST-OUEST - CORRECTION D'EXCENTRICITE demande à
chaque correction de l'ordre de 5 m/s limité à 12 m/s maximum.
Une
correction d'inclinaison de 0.2 degré ( 0°.1 ramené à - 0°.1 ) coûte environ 11
m/s. c'est la correction la plus onéreuse et malheureusement inévitable sous
l'effet de la perturbation lunaire notamment.
La
périodicité du maintien à poste n'est pas fixe, elle dépend du positionnement
sur l'équateur, du type de satellite. En général elle est de l'ordre de 2
semaines (TELECOM 2 ), 3 semaines (TELECOM 3 )
Le
budget annuel est de l'ordre de :
o
Corrections(NORD-SUD) de l'ordre de 50 m/s
o
Corrections(EST-OUEST) de l'ordre de 2 à 3 m/s
REMARQUE
FINALE : La qualité et la précision d'un tir géostationnaire, permettent de
gagner énormément sur la durée de vie d'un satellite. Le gain sur la correction
d'orbite durant la mise à poste devient une réserve supplémentaire de vitesse
pour la maintenance à poste.
VI UTILISATION D'UNE ORBITE
SUPERSYNCHRONE:
La
tendance actuelle, depuis quelques années, est d'utiliser une orbite primaire
très particulière, appelée ORBITE DE TRANSFERT SUPERSYNCHRONE (SSTO =
SuperSynchronous Transfert Orbit ).
A
titre d'exemples :
1
- Satellite géostationnaire ORION F1 lancé par une fusée ATLAS IIA le 29/11/94
sur une SSTO d'apogée 123500 km, pour terminer après manœuvres à 37°.5 de
longitude en géostationnaire.
2
- Lancement par une fusée ARIANE 44LP d'un satellite de télécommunication US
TELSTAR-7 en septembre 1999 sur une SSTO de périgée 200 km et d'apogée de
l'ordre de 60000 km, inclinée de 7°. Son stationnement géostationnaire est de
129° et la durée de vie prévue de 15 ans.
1°) Description de l'orbite SSTO :
Une
orbite SSTO est une première orbite de transfert, obtenue après la séparation
lanceur, présentant un apogée de très haute altitude et une inclinaison non
négligeable. Il y a quelques années, on parlait de passage par l'infini.
Une série de manœuvres permettra ensuite de ramener le satellite à sa longitude
de stationnement géostationnaire.
2°) Rôle de l'orbite SSTO :
Vous
constaterez plus tard ( voir le cours sur les paramètres
orbitaux ) que l'INCLINAISON
ORBITALE dépend
directement de la latitude du point d'injection qui, pour des tirs plein Est,
profitant au maximum de la rotation terrestre est égale à celle de la base
terrestre de tir : citons les inclinaisons classiques
Environ
23° à 27° pour les tirs US
De
l'ordre de 7° pour les lancements Ariane à partir de Kourou
Enfin
sensiblement 45°à 52° pour des lancements russes.
Pour
un satellite de télécommunication l'orbite finale est équatoriale et la
position extrêmement précise.
On
comprend bien dès lors que 2 types de correction sont à effectuer :
Sur
la forme de l'orbite
Sur
l'inclinaison orbitale qui doit être en théorie ramenée à 0°.
Or
corriger une inclinaison ne peut se faire qu'au dessus d'un nœud ( voir
corrections orbitales
) et amène à faire tourner le vecteur vitesse avec ou sans changement de
module. Dans le meilleur des cas pour une vitesse d'apogée de l'ordre de 1500
m/s une correction de 1° coûte 26.2 m/s, et pour 25° 649.3 m/s. On constate
donc un coût propulsif important, dont l'économie, même partielle, pourrait
allonger la durée de vie, notamment en maintenance d'orbite.
Le
bons sens montre que la norme de la correction de vitesse est d'autant plus
petite, pour une rotation fixée, que la vitesse initiale est petite. L'apogée
est donc le point idéal et le reste quasiment même si la correction affecte
aussi la forme de l'orbite.
Avec
un apogée "très haut" et donc une faible vitesse à cet apogée, la
SSTO devient intéressante.
NB:
On n'oubliera pas cependant que pour "monter" haut, il faut une
vitesse d'injection plus grande, ce qui pénalise le lanceur et fait perdre de
la masse utile satellite.
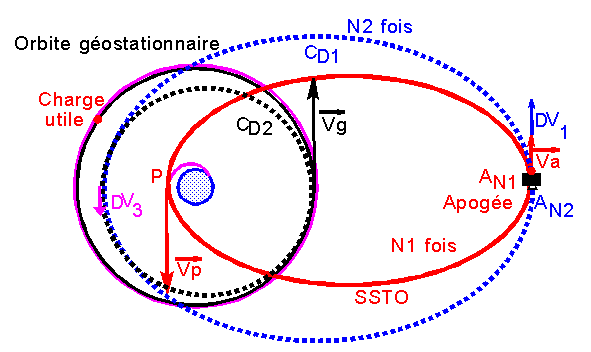
3°) Détail de la mise en orbite :
Le
schéma ci-dessous résume la procédure de mise à poste géostationnaire:
Injection
initiale en P ou au voisinage de P ( périgée ) sur une SSTO.( orbite rouge),
parcourue, suivant les besoins N1 fois. Cette orbite est de grande
période, de l'ordre de 1 à 2 jours.
On
réalise à l'apogée de la SSTO une correction DV1 à la fois de
l'inclinaison qui est ramenée à 0° ou au voisinage de 0°, par une rotation du
vecteur vitesse d'un angle a, et du
périgée remonté pratiquement au niveau géostationnaire.
L'orbite
elliptique CD1 (dite de dérive, en pointillés bleus), est parcourue suivant le
cas N2 fois. Sa période est encore plus grande que celle de la SSTO.
L'apogée
est ensuite placé au niveau géostationnaire par une manœuvre DV3, on est alors
sur une autre orbite de dérive CD2.
Le
périgée définitivement est enfin calé au bon niveau par une dernière opération
opérée à l'apogée de CD2. Naturellement cette dernière opération est
en pratique plus complexe, nécessitant des réglages très fins.
NB1:
De toute évidence, comme le satellite repasse toujours par le lieu où une correction
de trajectoire est réalisée, lorsque le géostationnaire est à poste,
obligatoirement la dernière correction a lieu à cet endroit. Toutes les orbites
ont en commun la propriété d'avoir le grand axe comme ligne des nœuds, de manière à avoir l'apogée sur l'équateur terrestre.
Ainsi en général la longitude vernale de la ligne des
noeuds vaut |W|= 180°, c'est le cas des lancements Ariane.
NB2
: L'ensemble de la mise en orbite après l'étape 2 est analogue à celui d'un tir
GTO classique. On notera tout de même que plus l'apogée est haut, plus longue
sera la période de la SSTO et donc la durée de la manœuvre, pouvant atteindre 1
à 3 semaines.
4°) Inconvénients et avantages liés à une SSTO :
o
Durée
de la mise à poste : elle est, nous l'avons souligné précédemment, relativement longue,
classiquement de l'ordre de 10 à 15 jours.
o
Problèmes
technologiques
: vue la grande altitude de l'apogée, il est clair que le pilotage ou la
restitution d'altitude demande des senseurs terrestres particuliers. De même,
les liaisons Centre de contrôle-Satellite vont demander des équipements
spécifiques grandes distances.
o
Effets
des perturbations
: avec un apogée pouvant atteindre 150000 km, la perturbation
luni-solaire
devient non négligeable et affecte notamment la ligne des nœuds et la ligne des
apsides. La vitesse angulaire de rotation qui peut devenir importante devra
être prise en compte dès avant le lancement, dans la stratégie de mise à poste.
De plus, la perturbation luni-solaire affecte l'altitude du périgée, qu'il faut
surveiller pour éviter une rentrée atmosphérique prématurée du satellite.
o
Intérêt : ce type d'orbite est intéressant
dans le cas d'un lanceur sur-performant, permettant d'atteindre une plus grande
vitesse d'injection et diminuant en conséquence le coût de mise à poste. A
contrario, pour un lanceur sous-performant, on utilisera une orbite de
transfert SOUS-SYNCHRONE, c'est à dire avec un apogée très en dessous du niveau
géostationnaire, laissant à la motorisation satellite le soin de toute la mise
à poste.
![]()
Guiziou Robert, septembre 2007, sept
2011