La théorie de Gibbs permet de déterminer complètement la trajectoire par la seule connaissance de trois rayons vecteurs à trois dates.

Données :

Trois positions de la sonde dans le repère de référence est S I J K héliocentrique écliptique dans lequel seront faits tous les calculs.  

1°) Avec la théorie de Gibbs déduire :

Le paramètre p en km

L'excentricité e

Le demi grand axe a en km

Les vecteurs P, Q, W du repère périfocal associe à la trajectoire

2°) Calculer le vecteur vitesse V à la date du 03/04/1994 0 h

2°) Calculs de Gibbs :

Gibbs introduit les trois vecteurs N S et D définis comme suit:

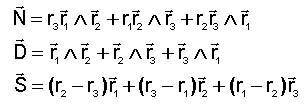
 De ces vecteurs on peut déduire :

 Le vecteur vitesse se calcule par :

 Le vecteur excentricité et le paramètre p s'obtiennent par :

 Voici le résultat des calculs :

Vecteur D :

D(1) = 5.39603 10⁸ km D(2) = -4.527116 10⁸ km D(3) = 3.52789 10⁸ km

Vecteur N :

N(1) = 7.148056 10¹² km N(2) = 7-5.997017 10¹² km N(3) = 4.675616 10¹² km

Vecteur S :

S(1) = 3.54262 10⁸ km S(2) = 4.225597 10⁸ km S(3) = -1.6908388 10⁵ km

Vecteur V1 :

V(1) = 4.9492 km/s V(2) = 7.42524 km/s V(3) = 1.958377 km/s

Le paramètre vaut p=13248.17 km et l'excentricité 0.7002677

Les paramètres orbitaux sont fournis par la routine rv_par_w.exe qui donne sensiblement :

C'est une orbite de type Molnya