PROJET : PROPULSION ELECTRIQUE ET DEORBITATION D'UN SATELLITE

NB : L'idée du projet est venue d'un e donnée du CNES d'un de ses ouvrages de base : TECHNIQUE & TECHNOLOGIES DES VEHICULES SPATIAUX , Volume 1, Cépadues Editions, page 280.

La constellation Skybridge est un système de télécommunications, à haut débit via les satellites , composé de 80 satellites en orbite circulaire à 1457 km. Lancement de 2001 et système totalement opérationnel en 2004-2005.

En fin de vie chaque satellite, situé à une altitude relativement basse, présente un danger de collisions avec d'autres mobiles, satellites, lanceurs ou stations spatiales. Il est donc nécessaire de précipiter leur fin, en les amenant à "brûler" dans l'atmosphère.

Pour cela, une manœuvre de déorbitation est obligatoire pour les amener vers 300 km ou une rentrée naturelle sous l'effet du freinage atmosphérique achèvera la "mise à mort".

Il est clair que l'objet de ce projet vaudra pour d'autres applications.

I.PRESENTATION :

Ce bureau d'étude est l'occasion de mettre en œuvre une propulsion exotique pour une correction de trajectoire en continu, à faible poussée. Vous pourrez utiliser les équations de Gauss ou les équations classiques du mouvement et par comparaison valider les résultats, et ensuite les confronter, dans des cas simplifié à un calcul analytique direct.

Un contact avec MATRA MARCONI SPACE , le CNES ou l'ONERA pourrait être utile.

II ETUDES ET CALCULS A REALISER :

TRAVAIL 1 : Vous présenterez succinctement, les principales constellations actuellement en service ou celles à venir, leur intérêt et le mode de lancement d'un tel grand nombre de satellites.

TRAVAIL 2 : Vous exposerez les caractéristiques essentielles de la propulsion électrique et ses applications pratiques.

Nous projetons d'utiliser la PROPULSION ELECTRIQUE pour "spiraler" autour de la terre, afin de diminuer l'énergie de l'ellipse de départ à 1457 km pour "descendre" jusqu'à 300 km sol.

1°) DONNEES :

J'ai conservé les données du CNES:

Module de la poussée F=0.083 N

Impulsion spécifique Isp=1450 secondes ( attention aux unités)

Masse du satellite en fin de vie, avant déorbitation : Mo=1060 kg

Orbite opérationnelle initiale Zo=1457 km

Orbite visée de fin de déorbitation Zf=300 km

Pour la modélisation du freinage atmosphérique :

Surface de référence de la traînée S=23.5 m²

Coefficient de frottement C_D=2.4

Masse volumique de l'air modélisée ainsi par le modèle de JACCHIA qui donne sous forme de tables :

log₁₀ ( Inverse de r(Z) ) : r(Z) masse volumique de l'air, mesurée en g/cm³ pour des altitudes Z entre120 et 1500 km du sol , suivant la température exosphérique T° en Kelvins, ici choisie à 1450 °K.

ALTITUDES: Z (km) =

[120;130;140;150;160;170;180;190;200;210;220;230;240;250;260;270;280;290;300;320;340;360;380;400;420;440; 460;480;500;520;540;560;580;600;620;640;660;680;700;720;740;760;780;800;850;900;950;1000;1050;1100;1150;1200;1250; 1300;1350;1400;1450;1500]

Pour une température de 1450°K : log₁₀(1/r) en g/cm³ =

[10.609;11.114;11.435;11.674;11.866;12.028;12.170;12.298;12.414;12.523;12.624;12.720;12.812;12.900;12.985;13.067; 13.147;13.224;13.300;13.446;13.585;13.720;13.849;13.975;14.096;14.214;14.328;14.440;14.549;14.655;14.760;14.862; 14.962;15.061;15.158;15.254;15.348;15.440;15.531;15.753;15.966;16.169;16.361;16.540;16.785;16.854;16.988;17.107; 17.211;17.302;17.384;17.456;17.522;17.582;17.638;17.691; 17.742;17.791]

Voir tables de Jacchia

En dessous de 120 km, la rentrée est considérée comme achevée, cependant vous pouvez suivre la capsule jusqu'au sol s'il en reste quelque chose en modélisant l'atmosphère avec airstand.pas, source en Pascal.

2°) PROCEDURE :

a) De 1457km à 300 km, descente en propulsion continue de mode rétrofusée, avec naturellement le freinage atmosphérique résiduel en supplément.

Vous intégrerez avec un algorithme de votre choix:

• Les équations résultant de la loi fondamentale écrite dans le repère géocentrique équatorial
• Les équations de Gauss donnant l'évolution des paramètres orbitaux osculateurs.

La comparaison des deux méthodes devrait confirmer par recoupement la validité des calculs. Vous indiquerez quels sont les paramètres orbitaux concernés. Le test d'arrêt de la propulsion entre en jeu à une altitude de 300 km.

TRAVAIL 3 : Validez votre intégration en supposant seulement la force F du moteur, en l'absence du frottement atmosphérique, et une masse constante M=1050 kg, alors que pour l'intégration exacte la masse diminue. Vous comparez alors à la relation suivante, que vous établirez avec l'équation de l'énergie spécifique:

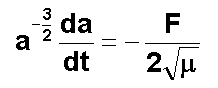
Vous retrouverez alors la durée de la descente à 300 km, qui est donc un peu supérieure à la durée réelle.

TRAVAIL 4 : Vous donnerez la masse d'ergols utilisée et le DV correspondant. Quelle est la durée de cette première phase ? A titre de comparaison, quelles sont les durées pour des forces 0.5 , 2, 4, 8 fois celle préconisée ?

TRAVAIL 5 : Vous donnerez vos commentaires sur les difficultés rencontrées avec les équations classiques ou celles de Gauss.

b) Au dessous de 300 km, il ne restera que le freinage atmosphérique.

Eventuellement, vous pouvez essayer d'étendre l'étude à un cas particulier de voyage interplanétaire, utilisant la poussée photonique. Naturellement, vous vous renseignerez sur l'adaptation des surfaces de voile convenant à cette propulsion.

3°) EXTRAPOLATION DE L'ETUDE :

Votre algorithme d'intégration étant au point, vous pouvez maintenant utiliser votre travail pour déborder de l'étude initiale, en calculant par exemple la durée de vie d'un satellite sous le seul effet de la traînée résiduelle, en fonction de l'altitude de 200 à 800 km par exemple. Vous montrerez un graphique de vos résultats et commenterez leur validité ( Méconnaissance de l'activité solaire, du coefficient de traînée, ...).

Guiziou décembre2002, sept 2011