|
PERTURBATION DUE A J2 |
|
CONTENU : Mis
à jour 11 janvier 1999, revu sept 2011 II Effets de la perturbation sur les paramètres orbitaux |
|
Pour
le spécialiste, parler de la perturbation due à J2 revient à étudier les
conséquences de l'aplatissement polaire de la terre sur l'orbite et le
mouvement orbital. On dira encore, en étant plus savant qu'on s'intéresse à l'harmonique
zonal (2,0).
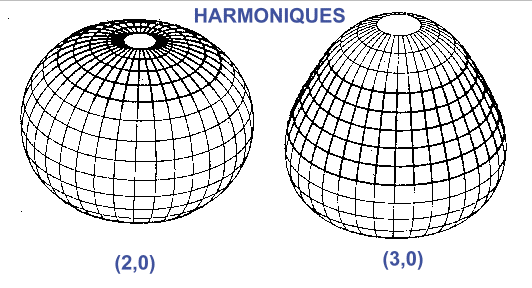
NB
: Avec l'harmonique zonal (3,0) on aurait pris en compte la forme de
"poire" de la terre, sous la forme du coefficient J3.
I POTENTIEL PERTURBATEUR
ET FORCE PERTURBATRICE ASSOCIEE :
Nous
en avons déjà parlé, le potentiel terrestre est développé en série, plus ou
moins complexe suivant les modèles. Le premier terme est le potentiel
newtonien. Les termes suivants représentent le potentiel perturbateur.
En ne prenant en compte que le premier terme de la
perturbation, on a le potentiel perturbateur du à J2.:
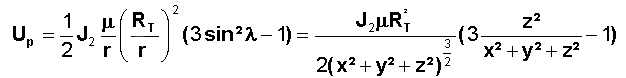
La force s'en déduit par le gradient, vous ferez le calcul
des composantes dans le repère géocentrique équatorial I J K avec K suivant
l'axe de la terre :
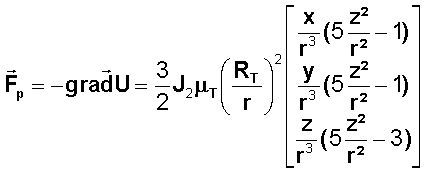
Une
transformation simple de l'expression de la force permet de la décomposer en 2
parties, l'une centrale qui modifie la vitesse orbitale et joue instantanément
sur les paramètres a et e en particulier, l'autre parallèle à l'axe de la rotation
terrestre, dont le sens dépend de la latitude. C'est précisément cette force
crée une composante normale Np de la perturbation, responsable d'après les
équations de Gauss de variations instantanées de i, w, W, M.
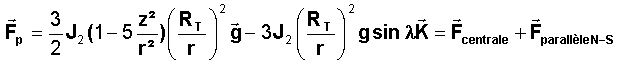
II EFFETS DE LA PERTURBATION :
Nous
ne pouvons pas rentrer dans le détail de tous les effets, certains étant de
valeur moyenne nulle mais fluctuant avec de courtes ou de longues périodes,
d'autres sont séculaires donnant des dérives linéaires des paramètres orbitaux.
Seules ces derniers sont préoccupants, dans la majorité des applications
courantes.
Vous
consulterez les exercices EX1 et EX2 pour comprendre la technique de
calcul des effets moyennés.
L'effet
moyen sur le demi grand axe a est nul, ce qui paraît logique avec une
perturbation dérivant d'un potentiel, l'énergie mécanique est conservative, en
moyenne.
Moins
évident, l'excentricité et l'inclinaison orbitale restent en moyenne
constantes.
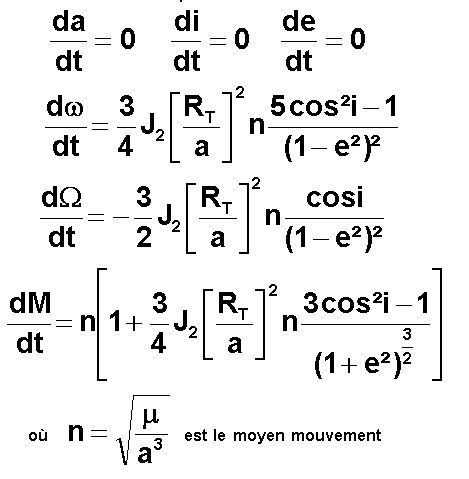
Par
contre, il apparaît des effets non négligeables sur w l'argument nodal du périgée, ce qui se traduit par
une rotation du grand axe dans son plan. Certes sur les orbites circulaires,
cela ne se voit pas directement cependant le mouvement orbital s'en trouve
affecté.
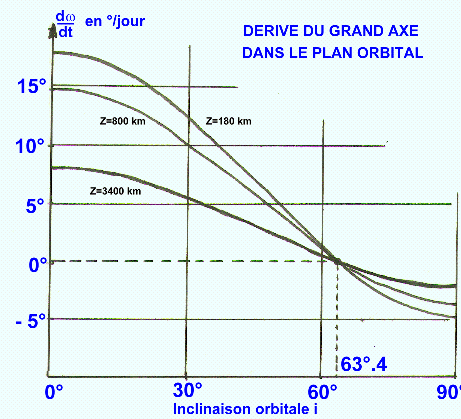
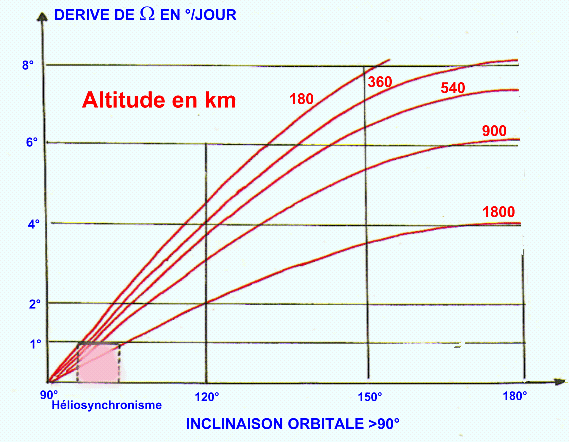
NB : Le graphe montre que l'inclinaison orbitale i=63°.4 annule
la dérive de w. Les soviétiques ne se privent pas d'utiliser une telle
inclinaison, qui leur autorise toutes les applications domestiques.
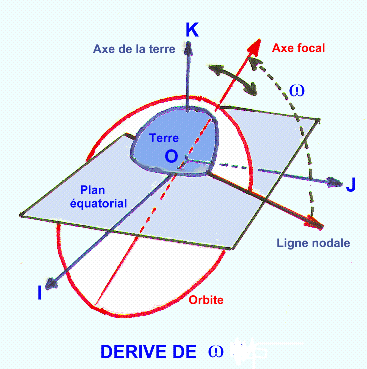
L'effet
le plus important est sans aucun doute la précession que J2 impose à la ligne
nodale dans le plan équatorial. A part l'ortbite polaire, tous les plans
orbitaux sont animés d'une précession dont les valeurs numériques sont visibles
sur le graphe :
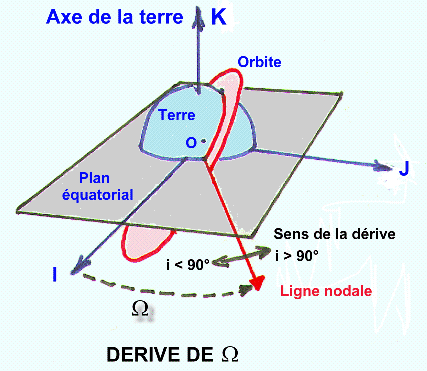
o
< 0
et donc rétrograde si i < 90°
o
>0
et donc dans le sens direct si i > +90°.
NB : Le graphe met en
évidence pour i > 90°, la plage des inclinaisons et altitudes respectant l'héliosynchronisme, dont l'application
est capitale pour les satellites d'imagerie ou de positionnement en particulier.
Si vous parcourez le chapitre consacré à l'exploitation de
l'héliosynchronisme, vous constaterez que cette propriété permet de survoler
une latitude donnée à une heure locale invariable, ce qui est d'un très grand
intérêt pratique.
Enfin
la perturbation J2 affecte le moyen mouvement n ou encore la vitesse angulaire
moyenne, créant ainsi un décalage horaire.
2°) EXEMPLES D'UTILISATION DE LA PERTURBATION :
Certaines
constellations utilisent de nombreux satellites gravitant sur des orbites de
même inclinaison mais dans des plans décalés, autant dire avec des longitudes
vernales W des nœuds différentes.
Un
moyen économique est d'utiliser un seul lanceur, plaçant des satellites dans un
même plan orbital, pour donner la bonne inclinaison, mais sur des orbites de
demi-grand axes différents. A chaque demi-grand axe va donc correspondre une
dérive spécifique de W qui finira par amener le satellite dans le bon plan. Il
suffira alors tout simplement de corriger le grand axe pour l'amener à sa
valeur nominale.
Exemple
donné par le CNES (
Cours de technologie spatialeVolume 1 page 268, CEPADUES EDITIONS) :
Constellation
de 12 satellites de plans espacés de 45°, à 1450 km d'altitude sol,
d'inclinaison 55°.
1-
Les 4 premiers sont immédiatement manœuvrés et placés sur l'orbite cible à 1450
km, inclinée à 45°
2-
8 sont déposés sur une orbite intermédiaire à 900 km, inclinée à 45°.
4
dérivent de 45° puis sont manœuvrés pour remonter à 1450 km
4
dérivent de 90° puis sont remontés sur la bonne orbite à 1450 km.
![]()
Guiziou Robert novembre 1998, sept
2011