![]()
CALCUL DE LA POSITION GPS
![]()
NB : cette rubrique m'a été inspirée par l'épreuve de modélisation 2016 de la banque commune école polytechnique-inter ENS. Mes calculs m'ont amené à une relation matricielle algorithmique un peu différente, que j'assume car ma simulation complète a confirmé mon étude. Retrouver le sujet.
Le cas envisagé très général, est celui d'un positionnement dans l'espace hors atmosphère, par exemple pour un véhicule d'une mission spatiale circumterrestre. La vitesse de la lumière est alors constante et non perturbée par les couches atmosphériques.
I DONNÉES ET POSITION DU PROBLÈME GÉNÉRAL :
Le repérage du récepteur et des satellites est réalisé en coordonnées cartésiennes, dans un même repère ( pas nécessairement lié à la terre ).
- x, y, z sont les coordonnées inconnues du récepteur qui cherche à se localiser, en liaison avec n ( n>=4) satellites Si.
- le satellite Si a pour coordonnées la matrice colonne di = [ xi yi zi ]T. Les coordonnées sont parfaitement connues et précises, calculées par le récepteur, sur la base des informations synchronisées envoyées par chaque satellite qui transmet ses éphémérides à l'instant T0, le même pour tous les satellites.
On notera donc D (3 x n) la matrice associée aux positions des satellites:
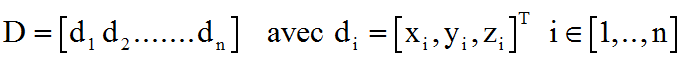
- Le récepteur reçoit le signal du satellite i à l'instant Tfi, l'écart de temps comprend la durée DTi du parcours à la vitesse de la lumière supposée constante dans un premier temps ( comme dans le vide, car elle dépend des caractéristiques du milieu traversé ) et un décalage DT supposé constant mais inconnu, considéré comme un biais du système récepteur, tenant à un défaut de synchronisation de l'horloge récepteur par rapport à celle commune des satellites parfaitement synchronisés. Seules les sommes de ces 2 temps, pour chaque satellite, sont connues du récepteur.
Tfi - T0 = DTi + DT
1°) Notion de pseudo-distance à un satellite:
Il est clair que la vraie distance d u récepteur ( en supposant la vitesse de propagation de la lumière c constante ) au satellite de n° i est:
Di = c DTi
Elle n'est donc pas connue et ne le sera que si DT est connu ou calculable.
On introduit alors la notion de pseudo-distance PDi = c ( Tfi - T0 )= c ( DTi + DT ) et on définit la matrice colonne connue du récepteur, des pseudo distances :
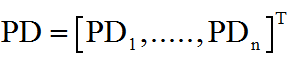
2°) Inconnues du problème de localisation :
Le traitement mathématique et informatique doit permettre de calculer simyltanément la position vraie ( x y z ) et DT à l'aide de la seule connaissance des n pseudo-distances.
On notera Q la matrice (4 x 1 ) des inconnues, tous ses éléments sont des distances, le décalage en temps est converti en distance après multiplication par c:
![]()
On comprend alors que le problème n'est pas habituel, puisque pour 4 inconnues à déterminer, nous disposons de n résultats, les n pseudo-distances. La méthode ne sera donc pas non plus classique. Le résultat ne pourra pas être exact mais seulement un meilleur résultat possible.
II TRADUCTION DU PROBLÈME :
1°) Formulation du problème :
L'idée est rechercher la meilleure solution, par exemple en essayant de minimiser par la méthode des moindres carrés la quantité
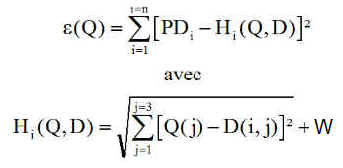
Hi (Q,D) est la pseudo distance au satellite Si, calculée à partir d'une position Q quelconque, associée à la matrice Q. Il faut donc trouver la meilleure matrice Q. Ce qui nous donnera simultanément la "meilleure position" et la "meilleure estimation de la valeur du biais" affectant le temps de réception.
2°) Linéarisation du problème:
On doit trouver Q minimisant la fonction e . Les fonctions Hi sont relativement complexes, mais malheureusement non linéaires. Compte tenu qu'une valeur approximative Q0 peut être calculée avec 4 satellites et par exemple DT = 0, on linéarise l'expression Hi (Q,D) autour de Q0 sous la forme
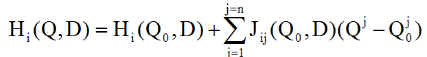
On a introduit alors la matrice jacobienne J(Q0,D)=[Jij] définie par les dérivées partielles
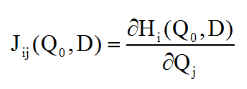
Cette matrice possède n lignes, comme le nombre de satellites et 4 colonnes, comme le nombre d'inconnues.
Traduction approchée du problème : avec un développement limité au premier ordre e s'écrit :
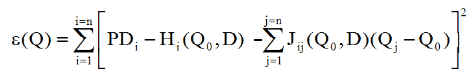
Traduisant la nullité du gradient de e par rapport à la variable Ql, il vient pour une dérivée partielle
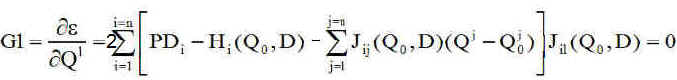
En notation matricielle ( le lecteur s'en convaincra ) le système des 4 dérivées nulles équivaut à rechercher le vecteur Q qui vérifie la relation matricielle:
|
|
ou encore
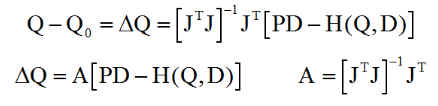
M = JTJ est une matrice carrée de dimension n.
III RÉSOLUTION :
La méthode choisie est de type de Newton-Raphson généralisée, par itération sur Q. On doit supposer que la matrice M = JTJ est inversible ce qui est équivalent à dire que son déterminant est différent de 0.
1°) Choix d'une valeur initiale :
On fixe une valeur de départ Q0 . On calcule ensuite Q par itération
2°) Calcul du jacobien J :
C'est la matrice ( n , 4 ) des dérivées de H par rapport à x y z et w, c est la vitesse de la lumière. On avait posé W = c.DT
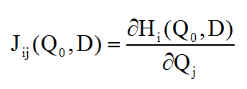 |
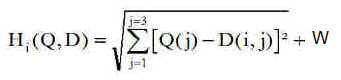 |
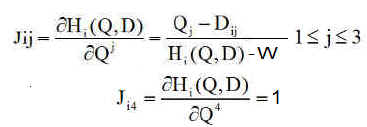 |
IV VÉRIFICATIONS DE L'ALGORITHME :
Il n'est pas nécessaire de prendre des coordonnées satellitaires réelles ni une position réelle du récepteur sur terre, pour vérifier la méthode.
Nous choisissons au départ au minimum 4 satellites dont les positions sont exactes et connues :
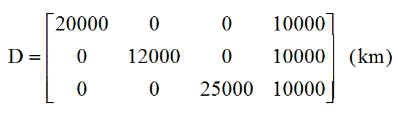
Nous situons notre station par ses coordonnées x y z et fixons l'écart de synchronisation à DT=10 ns ce qui fixe la solution Q à retrouver
Q=[2000000 4000000 6000000 c*10e-8] avec c = 299 792 458 m/s
Nous prenons un vecteur Q0 de départ voisin de plusieurs dizaines de km du point station et une synchronisation parfaite DT=0 s, alors qu'elle ne l'est pas en réalité, les données sont donc doublement biaisées. Voir en V l'estimation de ce point.
Q0=[2050000 3980000 6100000 0] en km
Les pseudo-distances mesurées sont les distances satellites-récepteur augmentées de c*10e-8 , sachant bien que l'écart de synchronisation n'est pas connu à ce stade. En clair, dans ces pseudo-distances, on ne peut distinguer la part de distance vraie parcourue par le signal de celle de son décalage temporel. Seule la somme est accessible par les mesures.
Conclusion : le programme itératif permet de retrouver très exactement, la position vraie du récepteur et simultanément le temps de désynchronisation de 10 ns, qui était inconnu au départ.
La résolution ne nécessite que 4 itérations, alors que l'erreur initiale de position est 58.23 km et celle de désynchronisation de 40 ns.
V RECHERCHE D'UNE POSITION DE DÉPART DE L"ALGORITHME ITÉRATIF :
Nous sommes maintenant en configuration réelle, où le récepteur doit d'abord trouver une position voisine de celle inconnue qu'il occupe, puis mettre en route les itérations qui vont donner le point exact ainsi que le temps de désynchronisation.
Nous ne connaissons pas l'erreur de désynchronisation des horloges satellites et récepteur. Par exemple, nous la prenons nulle avec pour distances vraies, les pseudo-distances D1,D2, D3, D4 au récepteur de 4 des n satellites de coordonnées (Xi Yi Zi ) utilisables. Rappelons que ces distances sont calculées avec les temps de propagation DTi mesurés par le récepteur et donc connues.
Sont donc connues les valeurs de Di, Xi, Yi, Zi, pour i =1 ... 4
Il est clair que ce système n'a que peu de chance d'avoir une solution. Tout au plus pourrait-on rechercher la solution "qui approche au mieux ' les quatre distances.
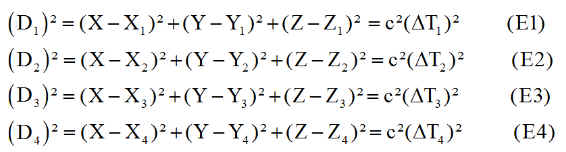
Par différence des équations E2 -E1 etc.. nous obtenons un système linéaire plus simple mais non équivalent ( 3 équations au lieu de 4 ) permettant un calcul de X Y Z acceptables.
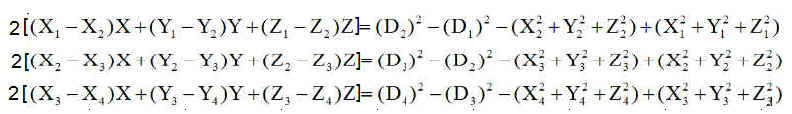
Le système linéaire se traduit par une relation simple :
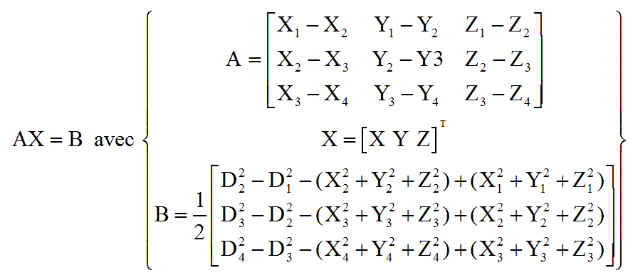
Si les trois rayons vecteurs récepteur-satellite ne sont pas coplanaires, la matrice A est inversible et le système possède une solution qui sera le point de départ de l'itération.
![]()
Ainsi, le vecteur Q inconnu est initialisé par Q0, en début d'itération Q0 = [TX c*50e-9 ]
VI TRAITEMENT INFORMATIQUE : retrouver les fichiers Matlab
Les calculs, formules et algorithme précédents ont été simulés sous Matlab, pour une remarquable confirmation, à la fois de la précision et de la rapidité de l'itération.
Un exemple de simulation est donné ci-dessous, avec l'exécution du programme iter_gps.m qui utilise les programmes jacobien.m et data_gps.m pour les données de la simulation.
************** COORDONNÉES DES ÉMETTEURS
***************
Ci-dessous en colonnes les 5 satellites émetteurs
satellites_colonne =
20000000 0
0
10000000 5000000
0
12000000 0
10000000 0
0
0
25000000 10000000 20000000
*********** PROTOCOLE DE VÉRIFICATION ***********
L'écart de synchronisation est choisi quelconque DT= 85 ns
Une position initiale a été calculée avec 4 satellites et une
désynchronisation nulle, comme pour un cas idéal
Les positions sont aléatoires de 99% à 100% des positions idéales,
affectées du décalage généré par l'écart de synchronisation DT
La position initiale du récepteur pour l'itération est:
X0= 2334504 m
Y0= 3984459 m
Z0= 5587386 m
La désynchronisation choisie au hasard est de 85 nanosecondes
La distance du point initial au point exact est de 22273 m
************** Données à vérifier *************
Rappels:
La position exacte du récepteur était:
Xs= 2345678 m
Ys= 4000010 m
Zs= 5598765 m
La désynchronisation choisie était de 40 nanosecondes
*************** Résultats calculés **************
Voici la localisation calculée après 3 itérations
pour une précision demandée de 30 m au plus
Le nombre de satellites accessibles est de 5 pour le cas envisagé
X= 2345678 m
Y= 4000010 m
Z= 5598765 m
L'écart de synchronisation calculé est de 40 nanosecondes
********************* Remarques ********************
Sur cet exemple la précision atteinte est de 0 m
L'écart de synchronisation est exactement retrouvé
*************************************************
* En faisant tourner plusieurs fois le programme, le point initial
*
* aléatoire, permet de voir que l'erreur de localisation reste très *
* faible de moins de 2 m, et que le nombre d'itérations est aussi *
* relativement petit.
*
*************************************************
ANNEXES
Annexe 1 --> Données
% Programme des données data_gps.m
% **************************************************************
% * SIMULATION D'UNE LOCALISATION GPS *
% * AVEC 5 SATELLITES *
% **************************************************************
clc,clear;
global N S D celerite_lumiere epsilon PD Q0 Q
epsilon=30; % Précision recherchée en m ( 30 m )
celerite_lumiere=299792458; % en m/s
% Positions exactes des N satellites, ici N=5
S=1000*[20000 0 0 10000 5000 ;
0 12000 0 10000 0;
0 0 25000 10000 20000]'; % en m
N=5; % Nombre de satellites émetteurs
% Q=[2000000 4000000 6000000 celerite_lumiere*40e-9]'; % Position exacte et intervalle de temps
% exact à retrouver W=celerite_lumiere*10e-8
Q=[2345678 4000010 5598765 celerite_lumiere*40e-9]';
% Calcul des distances exactes des N satellites à la station réceptrice théorique à retrouver
D(1)=norm(S(1,1:3)'-Q(1:3));
D(2)=norm(S(2,1:3)'-Q(1:3));
D(3)=norm(S(3,1:3)'-Q(1:3));
D(4)=norm(S(4,1:3)'-Q(1:3));
D(5)=norm(S(5,1:3)'-Q(1:3));
% ******************************** PSEUDO-DISTANCES MESUREES ********************************
% Calcul des pseudo_distances mesurées avec erreur sur le temps de synchronisation inconnu,
% mais supposé constant, pour toutes les mesures de temps satellite-récepteur ( 40 ns par exemple )
PD=D'+Q(4)*ones(N,1); % Elles sont connues et resteront constantes durant toute l'itération
% Sauf qu'on ne connait pas l'erreur de synchronisation ( ou encore W )
% ******************************* CALCUL D'UNE POSITION INITIALE ******************************
% On considère que les données PD mesurées sont bien sûr affectées d'une erreur de synchronisation,
% de 85 nanosecondes, ainsi les pseudo-distances seront:
PD_init(1:N)=(D(1:N))'+celerite_lumiere*85e-9*ones(N,1);
for i=1:3,
A(i,1:3)=S(i,1:3)-S(i+1,1:3);
end
for i=1:3,
B(i)=1/2*(PD_init(i+1)^2-PD_init(i)^2-(norm(S(i+1,1:3)))^2+(norm(S(i,1:3)))^2);
end
% ----------------------------------------------------------------------
% NB: les formules ont été vérifiées avec les distances exactes D(i) qui ont
% bien redonné la position exacte du satellite
% ----------------------------------------------------------------------
RR=ones(4,1)-0.01*rand(4,1); % Elaboration d'un nombre aléatoire entre 0.99 et 1
for i=1:3
QQ0(1:3)=inv(A)*B'; % Résolution du système linéaire introduit en paragraphe V de la théorie
Q0(i)=RR(i)*QQ0(i);
Q0(4)=celerite_lumiere*85e-9; % Ajout d'une erreur de synchronisation de 85 ns
end
% Q0=[2050000 3980000 6100000 0]; % Essai de vérification
end
-------------------------------------------------------------------------------------------------------------------
Annexe 2 --> Programmes des calculs
function y=jacobien(u);
% En entrée le vecteur Q à 4 inconnues
global D S N Q0 epsilon PD
Qpos=u; % Entrée de la position itérative
for i=1:N
HH(i)=norm(Qpos(1:3)-S(i,1:3)');
end
% Calcul du jacobien de l'itération
for i=1:N
for j=1:3
jacob(i,j)=(Qpos(j)-S(i,j))/HH(i);
end
end
jacob(1:N,4)=ones(N,1);
y=jacob;
end
% Programme d'itération iter_gps;
format long
data_gps;
global D S Q0 epsilon PD N
% Valeur initiale de Q = Q0
erreur=50; % Précision recherchée en m ( ici 50 m )
k=1;
Qiter=Q0';
% -------------------------------- Boucle ------------------------------
while erreur>=epsilon,
J=jacobien(Qiter);
A=inv(J'*J)*J'; % Inverse de la matrice multipliée par J'
for i=1:N
H(i)=norm(Qiter(1:3)-S(i,1:3)')+Qiter(4);
end
QQ2=Qiter+A*(PD-H');
erreur=norm(QQ2(1:3)-Qiter(1:3));
k=k+1;
Qiter=QQ2;
if erreur<=epsilon
disp(' ');
% Sortie de la position, en valeur entière au mètre près
Xc=fix(QQ2(1));Yc=fix(QQ2(2));Zc=fix(QQ2(3));
% Sortie de la désynchronisation en nanosecondes entières
Ecart_temps=fix(QQ2(4)/celerite_lumiere*1e9);
y=[Xc Yc Zc Ecart_temps]';
disp(' ************** COORDONNEES DES EMETTEURS ***************');
disp([' Ci-dessous en colonnes les ' num2str(N) ' satellites émetteurs']);
satellites_colonne=S',
disp(' ');
disp(' *********** PROTOCOLE DE VERIFICATION ***********');
disp(' L''écart de synchronisation est choisi quelconque DT= 85 ns');
disp(' Une position initiale a été calculée avec 4 satellites et une');
disp(' désynchronisation nulle, comme pour un cas idéal');
disp(' Les positions sont aléatoires de 99% à 100% des positions idéales,');
disp(' affectées du décalage généré par l''écart de synchronisation DT');
disp(' ');
disp(' La position initiale du récepteur pour l''itération est:');
disp([' X0= ' int2str(fix(Q0(1))) ' m']);
disp([' Y0= ' int2str(fix(Q0(2))) ' m']);
disp([' Z0= ' int2str(fix(Q0(3))) ' m']);
disp(' ');
disp([' La désynchronisation choisie au hasard est de ' int2str(fix(Q0(4)/celerite_lumiere*1e9)) ' nanosecondes']);
disp(' ');
disp([' La distance du point initial au point exact est de ' int2str(fix(norm(Q-Q0'))) ' m']);
disp(' ');
disp(' ************** Données à vérifier *************');
disp(' Rappels:');
disp(' La position exacte du récepteur était:');
disp([' Xs= ' int2str(fix(Q(1))) ' m']);
disp([' Ys= ' int2str(fix(Q(2))) ' m']);
disp([' Zs= ' int2str(fix(Q(3))) ' m']);
disp(' ');
disp([' La désynchronisation choisie était de ' int2str(fix(Q(4)/celerite_lumiere*1e9)) ' nanosecondes']);
disp(' ');
disp(' *************** Résultats calculés **************');
disp([' Voici la localisation calculée après ' int2str(k) ' itérations']);
disp([' pour une précision demandée de ' int2str(epsilon) ' m au plus']);
disp([' Le nombre de satellites accessibles est de ' int2str(N) ' pour le cas envisagé']);
disp(' ');
disp([' X= ' int2str(Xc) ' m']);
disp([' Y= ' int2str(Yc) ' m']);
disp([' Z= ' int2str(Zc) ' m']);
disp(' ');
disp([' L''écart de synchronisation calculé est de ' int2str(Ecart_temps) ' nanosecondes']);
disp(' ');
precision=norm(y(1:3)-Q(1:3));
disp(' ********************* Remarques ********************');
disp([' Sur cet exemple la précision atteinte est de ' num2str(precision) ' m']);
disp(' L''écart de synchronisation est exactement retrouvé');
disp(' ');
disp(' *********************************************************************')
disp(' * En faisant tourner plusieurs fois le programme, le point initial *')
disp(' * aléatoire, permet de voir que l''erreur de localisation reste très *')
disp(' * faible de moins de 2 m, et que le nombre d''itérations est aussi *')
disp(' * relativement petit *')
disp(' *********************************************************************')
break; % Sortie de la boucle
end
if k==5000
disp(' Non convergence du processus');
break;
end
end
% ----------------------------------- Fin boucle --------------------------
end.
************************************************* Fin de la rubrique *******************************************
Guiziou Robert juin 2016